[python] การทำข้อมูลให้เป็นมาตรฐานเพื่อการเรียนรู้ของเครื่อง
เขียนเมื่อ 2016/11/24 22:30
แก้ไขล่าสุด 2022/07/21 15:25
ครั้งก่อนได้เขียนถึงเรื่องการแบ่งข้อมูลด้วยการวิเคราะห์การถดถอยโลจิสติกไป https://phyblas.hinaboshi.com/20161103
แต่ก็ได้ทิ้งท้ายไว้ว่ายังมีหลายอย่างที่ต้องปรับปรุงอีก หนึ่งในนั้นก็คือเรื่องของการทำให้เป็นมาตรฐาน (标准化, standardize)
การทำให้เป็นมาตรฐานก็คือการแปลงหน่วยของข้อมูลทั้งหมดในชุดข้อมูลให้มีค่าเฉลี่ยอยู่ที่ 0 และส่วนเบี่ยงเบนมาตรฐานเป็น 1
สามารถทำได้โดยหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของข้อมูลทั้งหมด จากนั้นเอาค่าเฉลี่ยไปหักลบออกจากข้อมูลทุกตัว แล้วก็หารด้วยค่าส่วนเบี่ยงเบนมาตรฐาน
กล่าวคือ
การทำให้เป็นมาตรฐานโดยใช้ numpy
การแปลงค่าในอาเรย์ของ numpy ให้เป็นมาตรฐานในไพธอนทำได้ง่ายๆ เช่น ยกตัวอย่างลองสร้างอาเรย์ซึ่งมีเลข ๖ ตัว จากนั้นก็ทำการหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานแล้วก็นำมาใช้แปลงเลขทั้งหมดให้เป็นมาตรฐาน
ได้
จะเห็นว่าข้อมูลถูกเปลี่ยนให้มีค่าเฉลี่ยที่ 0 และกระจายอยู่ด้วยค่าที่ไม่ไกลจาก 0 ไปมาก
โดยทั่วไปแล้วข้อมูลที่นำมาใช้จะอยู่ในรูปของตัวแปรหลายตัวที่เรียงกันอยู่ในลักษณะที่เป็นอาเรย์สองมิติแบบนี้
เช่นเอาอาเรย์หนึ่งมิติสองตัวที่มีจำนวนข้อมูลเท่ากันมาต่อกัน
ได้
แต่ละหลักของข้อมูลคือข้อมูลคนละสิ่งกัน ดังนั้นเวลาทำให้เป็นมาตรฐานก็ต่างคนต่างทำแยกกัน ซึ่งสามารถทำได้โดยที่ใส่เลข 0 (หรือ axis=0) หมายถึงว่าให้หาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของทุกแถวในแต่ละหลักแยกกัน
ได้
การทำให้เป็นมาตรฐานโดยใช้ sklearn
sklearn เป็นมอดูลที่มีคำสั่งต่างๆมากมายที่ช่วยในเรื่องการเรียนรู้ของเครื่อง ก่อนหน้านี้ยังไม่เคยมีโอกาสได้เขียนถึง แต่หากใครตั้งใจจะเขียนโปรแกรมสำหรับการเรียนรู้ของเครื่องอยู่แล้วก็เป็นมอดูลที่ขาดไม่ได้ดังนั้นจึงควรจะติดตั้งเอาไว้เพื่อให้ใช้งานได้เสมอ เช่นเดียวกับ numpy, scipy และ matplotlib
หากใช้มอดูล sklearn เข้าช่วยก็จะสามารถจัดการเรื่องทำข้อมูลให้เป็นมาตรฐานได้ง่ายดายสะดวกมาก
โดยใน sklearn มีคลาส sklearn.preprocessing.StandardScaler ซึ่งใช้สำหรับการนี้
ตัวอย่างการใช้
ผลที่ได้คือได้ xy_sta เหมือนอย่างในตัวอย่างที่แล้วที่คำนวณเองได้
การใช้นั้นเริ่มแรกให้สร้างออบเจ็กต์ขึ้นจากคลาส StandardScaler (ในที่นี้ย่อเป็น Sta) จากนั้นก็นำออบเจ็กต์ตัวนั้นไปใช้โดยเริ่มจากใช้เมธอด fit เพื่อนำข้อมูลมาหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเพื่อนำมาใช้ในการแปลงต่อไป
จากนั้นจึงใช้เมธอด transform เพื่อทำการแปลงค่าให้เป็นค่าที่ปรับเป็นมาตรฐานแล้ว
อย่างไรก็ตาม ในการใช้โดยทั่วไปแล้วเรามักจะใช้ข้อมูลชุดหนึ่งเพื่อสร้างมาตรฐานในการแปลง เสร็จแล้วก็เอาข้อมูลชุดนั้นมาแปลงซะเอง กรณีแบบนี้มีวิธีที่ง่ายลัดขึ้นมาหน่อยนั่นคือใช้เมธอด fit_transform ดังนี้
เท่านี้ sta ก็ทำการคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของข้อมูล xy พร้อมกันนั้นก็คืนค่า xy ที่ทำให้เป็นมาตรฐานแล้วมาด้วย
ข้อมูลที่ใช้ใน fit จะต้องเป็นอาเรย์สองมิติซึ่งมีจำนวนหลักตามมิติของข้อมูล และมีจำนวนแถวตามจำนวนข้อมูลในชุด
หากต้องการรู้ค่าส่วนเบี่ยงเบนมาตรฐานก็ดูที่แอตทริบิวต์ sta.scale_ ส่วนค่าเฉลี่ยดูที่ sta.mean_
ทั้งค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานจะได้มาตามจำนวนหลักของชุดข้อมูล แต่ละหลักคิดแยกกันไม่ได้ขึ้นต่อกัน
และหากต้องการแปลงกลับก็ใช้เมธอด inverse_transform ได้ สะดวกดีมาก
การทำข้อมูลให้เป็นมาตรฐานเพื่อการเรียนรู้ของเครื่อง
วิธีการต่างๆที่ใช้สำหรับการเรียนรู้ของเครื่องนั้นโดยทั่วไปต้องการข้อมูลที่ถูกทำให้เป็นมาตรฐานแล้ว ไม่เช่นนั้นจะไม่สามารถทำงานได้ดี
การวิเคราะห์การถดถอยโลจิสติกเองก็เป็นเช่นนั้น หากไม่ทำข้อมูลให้เป็นมาตรฐานแล้วแม้จะป้อนข้อมูลสำหรับการเรียนรู้ให้แล้วทำการเรียนรู้ซ้ำไปสักแค่ไหนค่าน้ำหนักก็อาจไม่สามารถลู่เข้าสู่ค่าที่ต้องการได้เลย
ตัวอย่างการปลูกถั่วที่ได้ยกไปนั้นเป็นกรณีที่พอจะสามารถหาคำตอบได้โดยไม่ต้องทำให้เป็นมาตรฐานก็ได้ แต่ข้อมูลโดยทั่วไปอาจจะไม่ง่ายเช่นนั้นจึงควรทำอยู่เสมอ
ที่จริงวิธีการนอกจากการทำให้เป็นมาตรฐานแล้วยังมีอีกวิธีที่เรียกว่าการนอร์มาไลซ์ (normalize) คือการทำให้ข้อมูลตัวแปรต้นทั้งหมดกระจายอยู่ในระหว่าง 0 ถึง 1 ซึ่งก็เป็นวิธีที่สามารถใช้ได้เช่นกันแต่โดยทั่วไปแล้วการทำให้เป็นมาตรฐานจะค่อนข้างเหมาะสมมากกว่า ดังนั้นในที่นี้จะไม่พูดถึงการนอร์มาไลซ์ หากต้องการทำหลักการก็คล้ายๆกัน
ขอยกตัวอย่างที่แสดงให้เห็นว่าหากไม่ทำให้เป็นมาตรฐานแล้วจะไม่อาจให้ผลลัพธ์ดังที่ต้องการได้เลย
ในบทความที่แล้วยกตัวอย่างด้วยการปลูกถั่ว ครั้งนี้ก็จะขอใช้ตัวอย่างที่คล้ายๆกัน เพียงแต่เปลี่ยนจากปลูกถั่วเป็นปลูกผักกาดแทน
สมมุติว่าทดสอบปลูกผักกาด 600 ต้นลงในพื้นที่ 1000m x 200m แล้วพบว่าบางต้นโตบางต้นไม่โต ผลเป็นดังในภาพนี้
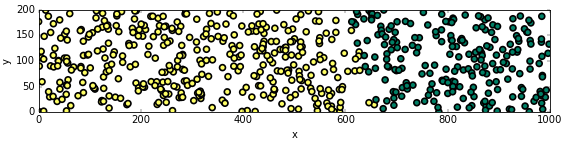
โดยที่สีเขียวคือโต สีเหลืองคือไม่โต
ภาพและข้อมูลสามารถได้มาจากโค้ดดังนี้
เหมือนกับคราวก่อน คราวนี้ก็จะใช้การวิเคราะห์การถดถอยโลจิสติกเพื่อหาเส้นแบ่งระหว่างดินส่วนที่ดี (ผักกาดโต) กับไม่ดี (ผักกาดไม่โต)
โดยจะใช้คลาส ThotthoiLogistic กับฟังก์ชัน sigmoid ซึ่งดึงมาจากบทความที่แล้ว ขอไม่เขียนใหม่ให้ซ้ำซ้อนในหน้านี้
ผลที่ได้จะพบว่าการเรียนรู้ไม่ค่อยจะก้าวหน้าไปตามที่ต้องการ
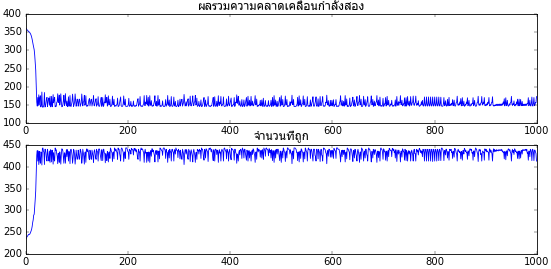
ลองเอามาวาดภาพการกระจายอีกครั้งพร้อมเส้นแบ่ง แล้วก็ใส่ขอบแดงให้อันที่ผิดด้วย
จะเห็นว่าเส้นแบ่งไม่ได้ใกล้เคียงกับที่ควรจะเป็นเลย และดูไม่มีวี่แววว่าจะถูกต้องไม่ว่าจะเรียนรู้อีกแค่ไหนก็ตาม
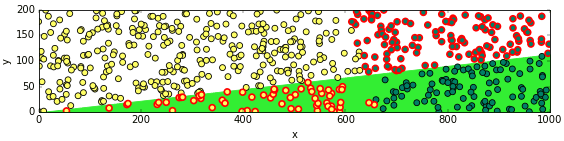
สังเกตได้ว่าเส้นแบ่งจะลากผ่านใกล้ๆกับจุด 0,0 ที่เป็นแบบนี้เพราะค่าไบแอส (ในที่นี้คือ w[0]) นั้นมีค่าใกล้เคียงกับ 0
สำหรับคำตอบที่ควรเป็นจริงๆนั้น w[0] ควรจะมากกว่าน้ำหนัก w[1] และ w[2] เป็นร้อยพันเท่า ดังที่เห็นได้จากสมการตั้งต้น
แต่เวลาที่ค่าน้ำหนักเปลี่ยนแปลงจากการเรียนรู้ในแต่ละทีแต่ละค่าถูกเปลี่ยนแปลงในอัตราที่เท่ากัน การที่เฉพาะ w[0] จะเปลี่ยนแปลงจนมีค่าเป็นพันนั้นเป็นเรื่องยาก
แต่หากทำการแก้ข้อมูลตำแหน่งแกน x และ y ให้เป็นมาตรฐานแล้ว w[0],w[1] และ w[2] จะพอๆกัน ปัญหานี้จะหมดไป
ลองทำดูโดยเขียนดังนี้
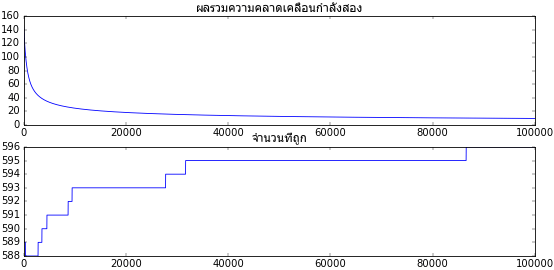
จะเห็นว่าพอทำแบบนี้แล้วการเรียนรู้ก็คืบหน้าเป็นไปตามที่ต้องการ แถมดูจากกราฟแล้วถ้าเพิ่มอัตราการเรียนรู้หรือจำนวนครั้งที่เรียนรู้ไปก็จะเข้าสู่คำตอบที่ต้องการได้โดยสมบูรณ์
เพียงแต่ว่าพอทำแบบนี้แล้วค่าของ x และ y จะถูกเปลี่ยนแปลงไปหมดทำให้ต้องแปลงกลับก่อนเพื่อจะสามารถเห็นภาพตามเดิม
ถ้าเราทำการปรับให้เป็นมาตรฐานแค่เฉพาะตอนก่อนเริ่มทำการเรียนรู้ จากนั้นพอเรียนรู้เสร็จก็ปรับค่าน้ำหนักให้เข้ากับข้อมูลเดิม แบบนี้ก็จะไม่ต้องอุตส่าห์ทำข้อมูลให้เป็นมาตรฐานก่อนเริ่มทำการเรียนรู้
วิธีการแปลงกลับสามารถพิสูจน์สมการได้ดังนี้
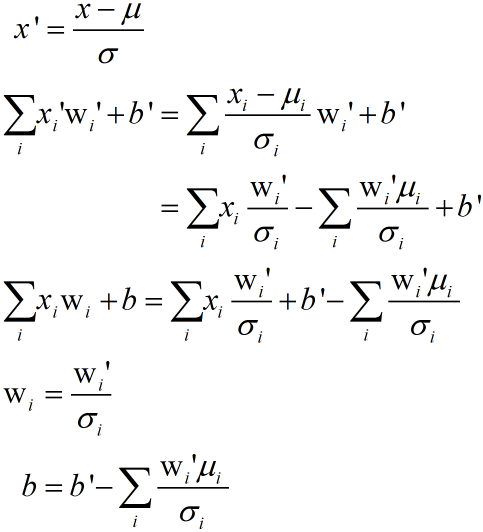
ในที่นี้ wi คือน้ำหนักของตัวแปรต้นแต่ละตัว b คือไบแอส ส่วนอันที่มี wi' และ b' คือน้ำหนักและไบแอสที่ได้จากการคำนวณเมื่อมีการทำให้เป็นมาตรฐานแล้ว เราต้องแปลงกลับเป็น wi และ b เพื่อจะนำมาใช้กับข้อมูลตัวแปรต้นเดิมที่ยังไม่ได้ทำให้เป็นมาตรฐาน
ลองทำการเขียนคลาสใหม่โดยแก้จาก ThotthoiLogistic อันเดิม สร้างเป็น ThotthoiLogistic อันใหม่ได้ดังนี้
โดยหลักแล้วที่เพิ่มไปก็แค่ในส่วนของเมธอด rianru เท่านั้น นอกนั้นไม่ค่อยต่างจากเดิม แต่แค่นี้ก็ทำให้การเรียนรู้ทำได้ราบรื่นขึ้นไม่มีปัญหาแล้ว
จากนั้นก็ลองนำมาใช้ดู
ผลที่ได้จะเห็นว่าเป็นไปตามที่ควรจะเป็น
อาจลองนำไปใช้กับข้อมูลชุดอื่นๆดูก็ได้เพื่อทดสอบว่าคลาสที่สร้างขึ้นใหม่นี้จะทำให้ผลที่ได้จะเป็นไปตามที่ต้องการได้ดีกว่าเดิมจริงๆ
อ้างอิง
แต่ก็ได้ทิ้งท้ายไว้ว่ายังมีหลายอย่างที่ต้องปรับปรุงอีก หนึ่งในนั้นก็คือเรื่องของการทำให้เป็นมาตรฐาน (标准化, standardize)
การทำให้เป็นมาตรฐานก็คือการแปลงหน่วยของข้อมูลทั้งหมดในชุดข้อมูลให้มีค่าเฉลี่ยอยู่ที่ 0 และส่วนเบี่ยงเบนมาตรฐานเป็น 1
สามารถทำได้โดยหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของข้อมูลทั้งหมด จากนั้นเอาค่าเฉลี่ยไปหักลบออกจากข้อมูลทุกตัว แล้วก็หารด้วยค่าส่วนเบี่ยงเบนมาตรฐาน
กล่าวคือ
x' = (x-μ)/σ
ข้อมูลที่ทำเป็นมาตรฐานแล้ว = (ข้อมูลเดิม - ค่าเฉลี่ย)/ส่วนเบี่ยงเบนมาตรฐาน
ข้อมูลที่ทำเป็นมาตรฐานแล้ว = (ข้อมูลเดิม - ค่าเฉลี่ย)/ส่วนเบี่ยงเบนมาตรฐาน
การทำให้เป็นมาตรฐานโดยใช้ numpy
การแปลงค่าในอาเรย์ของ numpy ให้เป็นมาตรฐานในไพธอนทำได้ง่ายๆ เช่น ยกตัวอย่างลองสร้างอาเรย์ซึ่งมีเลข ๖ ตัว จากนั้นก็ทำการหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานแล้วก็นำมาใช้แปลงเลขทั้งหมดให้เป็นมาตรฐาน
import numpy as np
x = np.array([1,3,6,7,13,144])
x_sta = (x-x.mean())/x.std()
print(x_sta)
x = np.array([1,3,6,7,13,144])
x_sta = (x-x.mean())/x.std()
print(x_sta)
ได้
[-0.54299879 -0.50421316 -0.44603472 -0.42664191 -0.31028502 2.23017361]
จะเห็นว่าข้อมูลถูกเปลี่ยนให้มีค่าเฉลี่ยที่ 0 และกระจายอยู่ด้วยค่าที่ไม่ไกลจาก 0 ไปมาก
โดยทั่วไปแล้วข้อมูลที่นำมาใช้จะอยู่ในรูปของตัวแปรหลายตัวที่เรียงกันอยู่ในลักษณะที่เป็นอาเรย์สองมิติแบบนี้
เช่นเอาอาเรย์หนึ่งมิติสองตัวที่มีจำนวนข้อมูลเท่ากันมาต่อกัน
x = np.array([1,3,6,7,13,14.])
y = np.array([811,892,901,934,945,995.])
xy = np.stack([x,y],1)
print(xy)
y = np.array([811,892,901,934,945,995.])
xy = np.stack([x,y],1)
print(xy)
ได้
[[ 1 811]
[ 3 892]
[ 6 901]
[ 7 934]
[ 13 945]
[ 14 995]]
[ 3 892]
[ 6 901]
[ 7 934]
[ 13 945]
[ 14 995]]
แต่ละหลักของข้อมูลคือข้อมูลคนละสิ่งกัน ดังนั้นเวลาทำให้เป็นมาตรฐานก็ต่างคนต่างทำแยกกัน ซึ่งสามารถทำได้โดยที่ใส่เลข 0 (หรือ axis=0) หมายถึงว่าให้หาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของทุกแถวในแต่ละหลักแยกกัน
xy_sta = (xy-xy.mean(0))/xy.std(0)
print(xy_sta)
print(xy_sta)
ได้
[[-1.32379273 -1.80415622]
[-0.90575292 -0.37144393]
[-0.27869321 -0.21225367]
[-0.0696733 0.37144393]
[ 1.18444612 0.56600979]
[ 1.39346603 1.4504001 ]]
[-0.90575292 -0.37144393]
[-0.27869321 -0.21225367]
[-0.0696733 0.37144393]
[ 1.18444612 0.56600979]
[ 1.39346603 1.4504001 ]]
การทำให้เป็นมาตรฐานโดยใช้ sklearn
sklearn เป็นมอดูลที่มีคำสั่งต่างๆมากมายที่ช่วยในเรื่องการเรียนรู้ของเครื่อง ก่อนหน้านี้ยังไม่เคยมีโอกาสได้เขียนถึง แต่หากใครตั้งใจจะเขียนโปรแกรมสำหรับการเรียนรู้ของเครื่องอยู่แล้วก็เป็นมอดูลที่ขาดไม่ได้ดังนั้นจึงควรจะติดตั้งเอาไว้เพื่อให้ใช้งานได้เสมอ เช่นเดียวกับ numpy, scipy และ matplotlib
หากใช้มอดูล sklearn เข้าช่วยก็จะสามารถจัดการเรื่องทำข้อมูลให้เป็นมาตรฐานได้ง่ายดายสะดวกมาก
โดยใน sklearn มีคลาส sklearn.preprocessing.StandardScaler ซึ่งใช้สำหรับการนี้
ตัวอย่างการใช้
from sklearn.preprocessing import StandardScaler as Sta
sta = Sta()
sta.fit(xy)
xy_sta = sta.transform(xy)
sta = Sta()
sta.fit(xy)
xy_sta = sta.transform(xy)
ผลที่ได้คือได้ xy_sta เหมือนอย่างในตัวอย่างที่แล้วที่คำนวณเองได้
การใช้นั้นเริ่มแรกให้สร้างออบเจ็กต์ขึ้นจากคลาส StandardScaler (ในที่นี้ย่อเป็น Sta) จากนั้นก็นำออบเจ็กต์ตัวนั้นไปใช้โดยเริ่มจากใช้เมธอด fit เพื่อนำข้อมูลมาหาค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานเพื่อนำมาใช้ในการแปลงต่อไป
จากนั้นจึงใช้เมธอด transform เพื่อทำการแปลงค่าให้เป็นค่าที่ปรับเป็นมาตรฐานแล้ว
อย่างไรก็ตาม ในการใช้โดยทั่วไปแล้วเรามักจะใช้ข้อมูลชุดหนึ่งเพื่อสร้างมาตรฐานในการแปลง เสร็จแล้วก็เอาข้อมูลชุดนั้นมาแปลงซะเอง กรณีแบบนี้มีวิธีที่ง่ายลัดขึ้นมาหน่อยนั่นคือใช้เมธอด fit_transform ดังนี้
xy_sta = sta.fit_transform(xy)
เท่านี้ sta ก็ทำการคำนวณค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานของข้อมูล xy พร้อมกันนั้นก็คืนค่า xy ที่ทำให้เป็นมาตรฐานแล้วมาด้วย
ข้อมูลที่ใช้ใน fit จะต้องเป็นอาเรย์สองมิติซึ่งมีจำนวนหลักตามมิติของข้อมูล และมีจำนวนแถวตามจำนวนข้อมูลในชุด
หากต้องการรู้ค่าส่วนเบี่ยงเบนมาตรฐานก็ดูที่แอตทริบิวต์ sta.scale_ ส่วนค่าเฉลี่ยดูที่ sta.mean_
print(sta.mean_) # ได้ [ 7.33333333 913. ]
print(sta.scale_) # ได้ [ 4.78423336 56.53612414]
print(sta.scale_) # ได้ [ 4.78423336 56.53612414]
ทั้งค่าเฉลี่ยและส่วนเบี่ยงเบนมาตรฐานจะได้มาตามจำนวนหลักของชุดข้อมูล แต่ละหลักคิดแยกกันไม่ได้ขึ้นต่อกัน
และหากต้องการแปลงกลับก็ใช้เมธอด inverse_transform ได้ สะดวกดีมาก
xy == sta.inverse_transform(xy_sta)
การทำข้อมูลให้เป็นมาตรฐานเพื่อการเรียนรู้ของเครื่อง
วิธีการต่างๆที่ใช้สำหรับการเรียนรู้ของเครื่องนั้นโดยทั่วไปต้องการข้อมูลที่ถูกทำให้เป็นมาตรฐานแล้ว ไม่เช่นนั้นจะไม่สามารถทำงานได้ดี
การวิเคราะห์การถดถอยโลจิสติกเองก็เป็นเช่นนั้น หากไม่ทำข้อมูลให้เป็นมาตรฐานแล้วแม้จะป้อนข้อมูลสำหรับการเรียนรู้ให้แล้วทำการเรียนรู้ซ้ำไปสักแค่ไหนค่าน้ำหนักก็อาจไม่สามารถลู่เข้าสู่ค่าที่ต้องการได้เลย
ตัวอย่างการปลูกถั่วที่ได้ยกไปนั้นเป็นกรณีที่พอจะสามารถหาคำตอบได้โดยไม่ต้องทำให้เป็นมาตรฐานก็ได้ แต่ข้อมูลโดยทั่วไปอาจจะไม่ง่ายเช่นนั้นจึงควรทำอยู่เสมอ
ที่จริงวิธีการนอกจากการทำให้เป็นมาตรฐานแล้วยังมีอีกวิธีที่เรียกว่าการนอร์มาไลซ์ (normalize) คือการทำให้ข้อมูลตัวแปรต้นทั้งหมดกระจายอยู่ในระหว่าง 0 ถึง 1 ซึ่งก็เป็นวิธีที่สามารถใช้ได้เช่นกันแต่โดยทั่วไปแล้วการทำให้เป็นมาตรฐานจะค่อนข้างเหมาะสมมากกว่า ดังนั้นในที่นี้จะไม่พูดถึงการนอร์มาไลซ์ หากต้องการทำหลักการก็คล้ายๆกัน
ขอยกตัวอย่างที่แสดงให้เห็นว่าหากไม่ทำให้เป็นมาตรฐานแล้วจะไม่อาจให้ผลลัพธ์ดังที่ต้องการได้เลย
ในบทความที่แล้วยกตัวอย่างด้วยการปลูกถั่ว ครั้งนี้ก็จะขอใช้ตัวอย่างที่คล้ายๆกัน เพียงแต่เปลี่ยนจากปลูกถั่วเป็นปลูกผักกาดแทน
สมมุติว่าทดสอบปลูกผักกาด 600 ต้นลงในพื้นที่ 1000m x 200m แล้วพบว่าบางต้นโตบางต้นไม่โต ผลเป็นดังในภาพนี้

โดยที่สีเขียวคือโต สีเหลืองคือไม่โต
ภาพและข้อมูลสามารถได้มาจากโค้ดดังนี้
import matplotlib.pyplot as plt
n_pluk = 600
x_phakkat = np.random.uniform(0,1000,n_pluk)
y_phakkat = np.random.uniform(0,200,n_pluk)
tomai = (3*x_phakkat+y_phakkat-2000>0).astype(int)
# บันทึกข้อมูลไว้ด้วย
np.savez('plukphakkat.npz',x=x_phakkat,y=y_phakkat,z=tomai)
plt.figure(figsize=[10,2])
plt.axes(aspect=1,xlim=[0,1000],ylim=[0,200],xlabel='x',ylabel='y')
plt.scatter(x_phakkat,y_phakkat,c=tomai,lw=2,s=50,edgecolor='k',cmap='summer_r')
plt.show()
n_pluk = 600
x_phakkat = np.random.uniform(0,1000,n_pluk)
y_phakkat = np.random.uniform(0,200,n_pluk)
tomai = (3*x_phakkat+y_phakkat-2000>0).astype(int)
# บันทึกข้อมูลไว้ด้วย
np.savez('plukphakkat.npz',x=x_phakkat,y=y_phakkat,z=tomai)
plt.figure(figsize=[10,2])
plt.axes(aspect=1,xlim=[0,1000],ylim=[0,200],xlabel='x',ylabel='y')
plt.scatter(x_phakkat,y_phakkat,c=tomai,lw=2,s=50,edgecolor='k',cmap='summer_r')
plt.show()
เหมือนกับคราวก่อน คราวนี้ก็จะใช้การวิเคราะห์การถดถอยโลจิสติกเพื่อหาเส้นแบ่งระหว่างดินส่วนที่ดี (ผักกาดโต) กับไม่ดี (ผักกาดไม่โต)
โดยจะใช้คลาส ThotthoiLogistic กับฟังก์ชัน sigmoid ซึ่งดึงมาจากบทความที่แล้ว ขอไม่เขียนใหม่ให้ซ้ำซ้อนในหน้านี้
eta = 0.00001 # อัตราการเรียนรู้
n_thamsam = 1000 # จำนวนครั้งที่ทำซ้ำ
# รวมอาเรย์ของ x และ y ได้เป็นอาเรย์สองมิติ
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
tl = ThotthoiLogistic(eta)
# เริ่มการเรียนรู้
tl.rianru(xy_phakkat,tomai,n_thamsam)
# วาดกราฟแสดงจำนวนที่ถูกกับความคลาดเคลื่อนรวมที่เปลี่ยนไปตามเวลา
plt.figure(figsize=[10,4])
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
n_thamsam = 1000 # จำนวนครั้งที่ทำซ้ำ
# รวมอาเรย์ของ x และ y ได้เป็นอาเรย์สองมิติ
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
tl = ThotthoiLogistic(eta)
# เริ่มการเรียนรู้
tl.rianru(xy_phakkat,tomai,n_thamsam)
# วาดกราฟแสดงจำนวนที่ถูกกับความคลาดเคลื่อนรวมที่เปลี่ยนไปตามเวลา
plt.figure(figsize=[10,4])
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
plt.show()
ผลที่ได้จะพบว่าการเรียนรู้ไม่ค่อยจะก้าวหน้าไปตามที่ต้องการ

ลองเอามาวาดภาพการกระจายอีกครั้งพร้อมเส้นแบ่ง แล้วก็ใส่ขอบแดงให้อันที่ผิดด้วย
x_sen = np.array([0,1000])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat)==tomai
plt.figure(figsize=[11,3])
plt.axes(aspect=1,xlim=[0,1000],ylim=[0,200],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[200,200],color='#33ee33')
plt.scatter(x_phakkat[thukmai==1],y_phakkat[thukmai==1],c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat[thukmai==0],y_phakkat[thukmai==0],c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat)==tomai
plt.figure(figsize=[11,3])
plt.axes(aspect=1,xlim=[0,1000],ylim=[0,200],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[200,200],color='#33ee33')
plt.scatter(x_phakkat[thukmai==1],y_phakkat[thukmai==1],c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat[thukmai==0],y_phakkat[thukmai==0],c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
จะเห็นว่าเส้นแบ่งไม่ได้ใกล้เคียงกับที่ควรจะเป็นเลย และดูไม่มีวี่แววว่าจะถูกต้องไม่ว่าจะเรียนรู้อีกแค่ไหนก็ตาม

สังเกตได้ว่าเส้นแบ่งจะลากผ่านใกล้ๆกับจุด 0,0 ที่เป็นแบบนี้เพราะค่าไบแอส (ในที่นี้คือ w[0]) นั้นมีค่าใกล้เคียงกับ 0
สำหรับคำตอบที่ควรเป็นจริงๆนั้น w[0] ควรจะมากกว่าน้ำหนัก w[1] และ w[2] เป็นร้อยพันเท่า ดังที่เห็นได้จากสมการตั้งต้น
แต่เวลาที่ค่าน้ำหนักเปลี่ยนแปลงจากการเรียนรู้ในแต่ละทีแต่ละค่าถูกเปลี่ยนแปลงในอัตราที่เท่ากัน การที่เฉพาะ w[0] จะเปลี่ยนแปลงจนมีค่าเป็นพันนั้นเป็นเรื่องยาก
แต่หากทำการแก้ข้อมูลตำแหน่งแกน x และ y ให้เป็นมาตรฐานแล้ว w[0],w[1] และ w[2] จะพอๆกัน ปัญหานี้จะหมดไป
ลองทำดูโดยเขียนดังนี้
plukphakkat = np.load('plukphakkat.npz')
x_phakkat = plukphakkat['x']
y_phakkat = plukphakkat['y']
tomai = plukphakkat['z']
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
sta = Sta()
# สร้างตัวแปรใหม่ขึ้นเก็บข้อมูลที่แปลงเป็นมาตรฐานแล้ว แล้วใช้ในการเรียนรู้
xy_phakkat_sta = sta.fit_transform(xy_phakkat)
tl = ThotthoiLogistic(eta)
print('ได้สมการเส้นแบ่งเขตเป็น %.5fx%+.5fy%+.5f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(tomai)))
plt.figure(11,5)
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
x_phakkat_sta = xy_phakkat_sta[:,0]
y_phakkat_sta = xy_phakkat_sta[:,1]
x_sen = np.array([x_phakkat_sta.min(),x_phakkat_sta.max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat_sta)==tomai
plt.figure(figsize=[6,6])
plt.axes(aspect=1,xlim=[x_phakkat_sta.min(),x_phakkat_sta.max()],
ylim=[y_phakkat_sta.min(),y_phakkat_sta.max()],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[y_phakkat_sta.min(),y_phakkat_sta.min()],color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[y_phakkat_sta.max(),y_phakkat_sta.max()],color='#33ee33')
plt.scatter(x_phakkat_sta[thukmai==1],y_phakkat_sta[thukmai==1],
c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat_sta[thukmai==0],y_phakkat_sta[thukmai==0],
c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
x_phakkat = plukphakkat['x']
y_phakkat = plukphakkat['y']
tomai = plukphakkat['z']
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
sta = Sta()
# สร้างตัวแปรใหม่ขึ้นเก็บข้อมูลที่แปลงเป็นมาตรฐานแล้ว แล้วใช้ในการเรียนรู้
xy_phakkat_sta = sta.fit_transform(xy_phakkat)
tl = ThotthoiLogistic(eta)
n_thamsam = 100000
tl.rianru(xy_phakkat_sta,tomai,n_thamsam)print('ได้สมการเส้นแบ่งเขตเป็น %.5fx%+.5fy%+.5f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(tomai)))
plt.figure(11,5)
ax = plt.subplot(211)
ax.set_title(u'ผลรวมความคลาดเคลื่อนกำลังสอง',fontname='Tahoma')
plt.plot(tl.sse)
ax = plt.subplot(212)
ax.set_title(u'จำนวนที่ถูก',fontname='Tahoma')
plt.plot(tl.thuktong)
x_phakkat_sta = xy_phakkat_sta[:,0]
y_phakkat_sta = xy_phakkat_sta[:,1]
x_sen = np.array([x_phakkat_sta.min(),x_phakkat_sta.max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat_sta)==tomai
plt.figure(figsize=[6,6])
plt.axes(aspect=1,xlim=[x_phakkat_sta.min(),x_phakkat_sta.max()],
ylim=[y_phakkat_sta.min(),y_phakkat_sta.max()],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[y_phakkat_sta.min(),y_phakkat_sta.min()],color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[y_phakkat_sta.max(),y_phakkat_sta.max()],color='#33ee33')
plt.scatter(x_phakkat_sta[thukmai==1],y_phakkat_sta[thukmai==1],
c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat_sta[thukmai==0],y_phakkat_sta[thukmai==0],
c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()


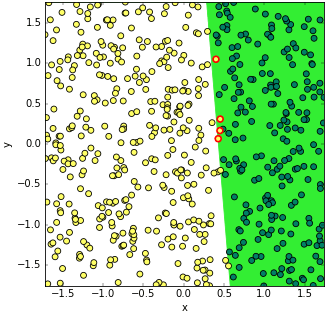
จะเห็นว่าพอทำแบบนี้แล้วการเรียนรู้ก็คืบหน้าเป็นไปตามที่ต้องการ แถมดูจากกราฟแล้วถ้าเพิ่มอัตราการเรียนรู้หรือจำนวนครั้งที่เรียนรู้ไปก็จะเข้าสู่คำตอบที่ต้องการได้โดยสมบูรณ์
เพียงแต่ว่าพอทำแบบนี้แล้วค่าของ x และ y จะถูกเปลี่ยนแปลงไปหมดทำให้ต้องแปลงกลับก่อนเพื่อจะสามารถเห็นภาพตามเดิม
ถ้าเราทำการปรับให้เป็นมาตรฐานแค่เฉพาะตอนก่อนเริ่มทำการเรียนรู้ จากนั้นพอเรียนรู้เสร็จก็ปรับค่าน้ำหนักให้เข้ากับข้อมูลเดิม แบบนี้ก็จะไม่ต้องอุตส่าห์ทำข้อมูลให้เป็นมาตรฐานก่อนเริ่มทำการเรียนรู้
วิธีการแปลงกลับสามารถพิสูจน์สมการได้ดังนี้
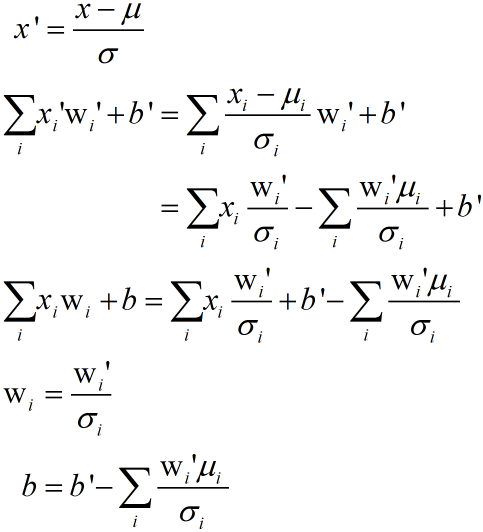
ในที่นี้ wi คือน้ำหนักของตัวแปรต้นแต่ละตัว b คือไบแอส ส่วนอันที่มี wi' และ b' คือน้ำหนักและไบแอสที่ได้จากการคำนวณเมื่อมีการทำให้เป็นมาตรฐานแล้ว เราต้องแปลงกลับเป็น wi และ b เพื่อจะนำมาใช้กับข้อมูลตัวแปรต้นเดิมที่ยังไม่ได้ทำให้เป็นมาตรฐาน
ลองทำการเขียนคลาสใหม่โดยแก้จาก ThotthoiLogistic อันเดิม สร้างเป็น ThotthoiLogistic อันใหม่ได้ดังนี้
import numpy as np
from sklearn.preprocessing import StandardScaler as Sta
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
# เรียนรู้
def rianru(self,X,z,n_thamsam):
self.sse = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
self.sta = Sta()
# ทำให้เป็นมาตรฐาน
X = self.sta.fit_transform(X)
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*phi*(1-phi)*(z-phi)*self.eta
self.w[1:] += np.dot(X.T,eee)
self.w[0] += eee.sum()
phi = self.ha_sigmoid(X)
# บันทึกผลในแต่ละรอบ
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(X,z)]
# ปรับค่าน้ำหนักให้เข้ากับข้อมูลเดิม
self.w[1:] /= self.sta.scale_
self.w[0] -= (self.w[1:]*self.sta.mean_).sum()
# ทำนายผล
def thamnai(self,X):
return self.ha_sigmoid(X)>0.5
# ฟังก์ชันกระตุ้น
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
# หาค่าเสียหาย
def ha_sse(self,X,z):
return ((z-self.ha_sigmoid(X))**2).sum()
from sklearn.preprocessing import StandardScaler as Sta
def sigmoid(x):
return 1/(1+np.exp(-x))
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
# เรียนรู้
def rianru(self,X,z,n_thamsam):
self.sse = []
self.thuktong = []
self.w = np.zeros(X.shape[1]+1)
self.sta = Sta()
# ทำให้เป็นมาตรฐาน
X = self.sta.fit_transform(X)
phi = self.ha_sigmoid(X)
for i in range(n_thamsam):
# ปรับค่าน้ำหนัก
eee = 2*phi*(1-phi)*(z-phi)*self.eta
self.w[1:] += np.dot(X.T,eee)
self.w[0] += eee.sum()
phi = self.ha_sigmoid(X)
# บันทึกผลในแต่ละรอบ
thukmai = np.abs(phi-z)<0.5
self.thuktong += [thukmai.sum()]
self.sse += [self.ha_sse(X,z)]
# ปรับค่าน้ำหนักให้เข้ากับข้อมูลเดิม
self.w[1:] /= self.sta.scale_
self.w[0] -= (self.w[1:]*self.sta.mean_).sum()
# ทำนายผล
def thamnai(self,X):
return self.ha_sigmoid(X)>0.5
# ฟังก์ชันกระตุ้น
def ha_sigmoid(self,X):
return sigmoid(np.dot(X,self.w[1:])+self.w[0])
# หาค่าเสียหาย
def ha_sse(self,X,z):
return ((z-self.ha_sigmoid(X))**2).sum()
โดยหลักแล้วที่เพิ่มไปก็แค่ในส่วนของเมธอด rianru เท่านั้น นอกนั้นไม่ค่อยต่างจากเดิม แต่แค่นี้ก็ทำให้การเรียนรู้ทำได้ราบรื่นขึ้นไม่มีปัญหาแล้ว
จากนั้นก็ลองนำมาใช้ดู
eta = 0.00002
n_thamsam = 80000
plukphakkat = np.load('plukphakkat.npz')
x_phakkat = plukphakkat['x']
y_phakkat = plukphakkat['y']
tomai = plukphakkat['z']
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
tl = ThotthoiLogistic(eta)
tl.rianru(xy_phakkat,tomai,n_thamsam)
print('ได้สมการเส้นแบ่งเขตเป็น %.5fx%+.5fy%+.5f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(tomai)))
x_sen = np.array([x_phakkat.min(),x_phakkat.max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat)==tomai
plt.figure(figsize=[11,3])
plt.axes(aspect=1,xlim=[x_phakkat.min(),x_phakkat.max()],ylim=[y_phakkat.min(),y_phakkat.max()],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[y_phakkat.min(),y_phakkat.min()],color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[y_phakkat.max(),y_phakkat.max()],color='#33ee33')
plt.scatter(x_phakkat[thukmai==1],y_phakkat[thukmai==1],c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat[thukmai==0],y_phakkat[thukmai==0],c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()
n_thamsam = 80000
plukphakkat = np.load('plukphakkat.npz')
x_phakkat = plukphakkat['x']
y_phakkat = plukphakkat['y']
tomai = plukphakkat['z']
xy_phakkat = np.stack([x_phakkat,y_phakkat],axis=1)
tl = ThotthoiLogistic(eta)
tl.rianru(xy_phakkat,tomai,n_thamsam)
print('ได้สมการเส้นแบ่งเขตเป็น %.5fx%+.5fy%+.5f = 0'%(tl.w[1],tl.w[2],tl.w[0]))
print('ทายถูกทั้งหมด %d จาก %d'%(tl.thuktong[-1],len(tomai)))
x_sen = np.array([x_phakkat.min(),x_phakkat.max()])
y_sen = -(tl.w[0]+tl.w[1]*x_sen)/tl.w[2]
thukmai = tl.thamnai(xy_phakkat)==tomai
plt.figure(figsize=[11,3])
plt.axes(aspect=1,xlim=[x_phakkat.min(),x_phakkat.max()],ylim=[y_phakkat.min(),y_phakkat.max()],xlabel='x',ylabel='y')
if(tl.w[1]*tl.w[2]<0):
plt.fill_between(x_sen,y_sen,[y_phakkat.min(),y_phakkat.min()],color='#33ee33')
else:
plt.fill_between(x_sen,y_sen,[y_phakkat.max(),y_phakkat.max()],color='#33ee33')
plt.scatter(x_phakkat[thukmai==1],y_phakkat[thukmai==1],c=tomai[thukmai==1],s=50,edgecolor='k',cmap='summer_r')
plt.scatter(x_phakkat[thukmai==0],y_phakkat[thukmai==0],c=tomai[thukmai==0],s=50,edgecolor='r',lw=2,cmap='summer_r')
plt.show()

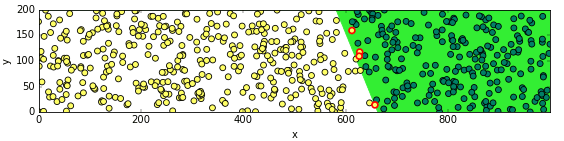
ผลที่ได้จะเห็นว่าเป็นไปตามที่ควรจะเป็น
อาจลองนำไปใช้กับข้อมูลชุดอื่นๆดูก็ได้เพื่อทดสอบว่าคลาสที่สร้างขึ้นใหม่นี้จะทำให้ผลที่ได้จะเป็นไปตามที่ต้องการได้ดีกว่าเดิมจริงๆ
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib