[python] วาดเส้นกราฟ ROC เพื่อประเมินผลการทำนาย
เขียนเมื่อ 2017/10/16 10:12
แก้ไขล่าสุด 2022/07/21 15:11
ในตอนที่แล้วได้แนะนำคะแนน f1 ไป https://phyblas.hinaboshi.com/20171014
นอกจากนี้แล้วก็ยังมีอีกวิธีหนึ่งในการพิจารณาประสิทธิภาพของแบบจำลองที่ใช้ทำนาย นั่นคือการดูกราฟ ROC (Receiver operating characteristic)
การจะอธิบายว่า ROC คืออะไรนั้นหากเริ่มจากอธิบายเป็นคำพูดเลยคงจะยาก ดังนั้นขอเริ่มด้วยการยกตัวอย่าง
สมมุติว่าข้อมูลการตรวจโรคจากสารในร่างกายของคน 1000 คนออกมาเป็นดังนี้ โดยแกนนอนคือปริมาณสาร a แกนนอนคือปริมาณสาร b สีเขียวคือผลบวก (มีโรค) สีน้ำเงินคือผลลบ (ไม่มีโรค)
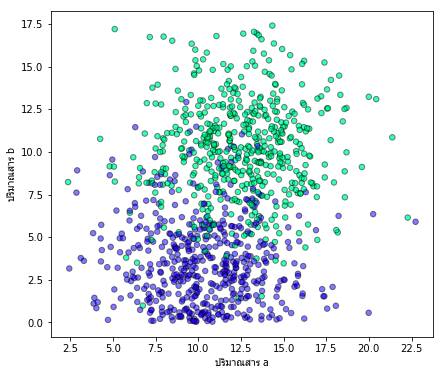
โค้ดสำหรับสร้างข้อมูลและวาดภาพเขียนได้ดังนี้
จากนั้นเราอาจใช้ LogisticRegression ของ sklearn เพื่อหาจุดแบ่งในการทำนายว่าถ้าตรวจพบคนไข้ที่มีปริมาณสาร a และสาร b เท่านี้จะสรุปว่าเป็นโรคหรือไม่
เราสามารถคำนวณความน่าจะเป็นของการเกิดผลบวกในแต่ละบริเวณได้โดยใช้เมธอด .predict_proba แบบนี้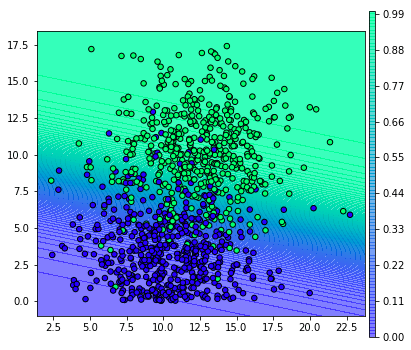
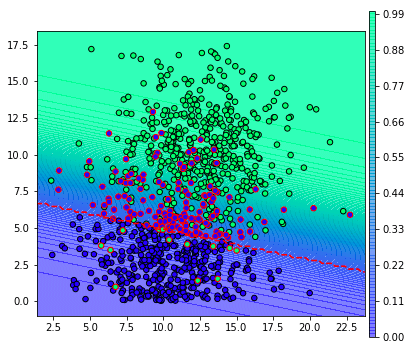
จากผลที่ได้ตรงนี้ ปกติแล้วเวลาตัดสินว่าผลเป็นบวกหรือเปล่าก็จะดูว่าความเป็นไปได้ถึง 0.5 หรือไม่ กล่าวคือ ขีดเส้นประสีแดงคั่นแบบนี้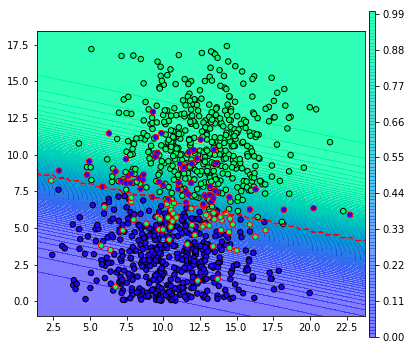
จุดที่ถูกล้อมกรอบสีแดงคือส่วนที่ถูกจำแนกผิด
อย่างไรก็ตาม หากเราลองปรับเปลี่ยนว่าให้ผลความน่าจะเป็นเป็น 0.8 จึงจะตัดสินว่าเป็นผลบวก จะเป็นแบบนี้ (ลองแก้ threshlod เป็น 0.8 แล้ววาดใหม่)
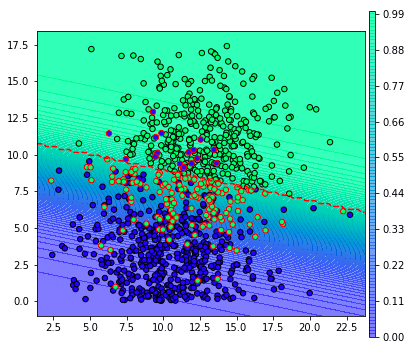
จะเห็นว่าผลที่ถูกทายว่าเป็นผลบวกมีน้อยลง
ส่วนทางกลับกันหากลองปรับให้เป็น 0.2 เส้นแบ่งก็จะเลื่อนลงมาด้านล่าง
การเปลี่ยนค่าจุดแบ่งนี้มีผลทำให้อัตราผลบวกจริง (true positive rate, tpr) และอัตราผลบวกปลอม (false positive rate, fpr) มีค่าเปลี่ยนแปลงไป
อัตราผลบวกจริง ก็คือค่าความระลึก (recall) ซึ่งกล่าวถึงไปในบทความก่อน คำนวณได้จาก
อัตราผลบวกจริง = บวกจริง/(บวกจริง+ลบปลอม)
ส่วนอัตราผลบวกปลอม คำนวณได้จาก
อัตราผลบวกปลอม = บวกปลอม/(บวกปลอม+ลบจริง)
ค่าทั้งสองนี้อาจคำนวณได้ดังนี้
threshold คือจุดแบ่ง อาจมีค่าตั้งแต่ 0 จนถึง 1 ค่าจุดแบ่งมีผลต่อค่า tpr และ fpr
แล้วถ้าหากเราลองทำการวาดกราฟที่แสดงความสัมพันธ์ระหว่างค่าจุดแบ่ง โดยเขียนตามนี้
ก็จะได้แบบนี้
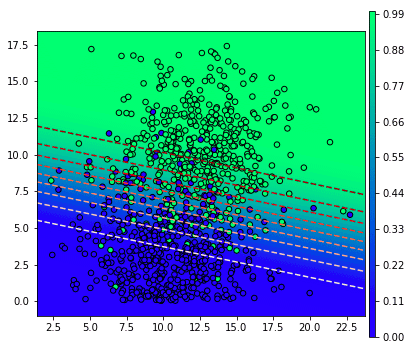
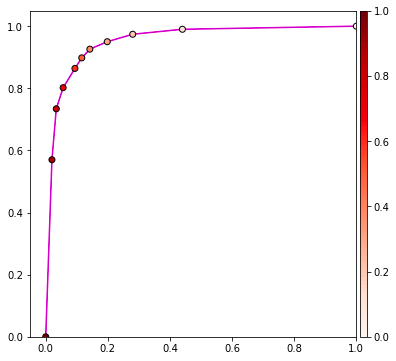
ในที่นี้สีของจุดในกราฟจะตรงกับสีของเส้นแบ่งในแผนภาพด้านบน
เส้นกราฟนี้ล่ะที่เรียกว่าเส้นกราฟ ROC
เส้นกราฟจะเริ่มจาก (0,0) และจบที่ (1,1) เสมอ เพราะถ้าให้ค่าจุดแบ่งเป็น 0 หมายความว่าผลที่ทายจะเป็นลบหมด ดังนั้นไม่ว่าบวกจริงหรือบวกปลอมก็จะมีอยู่ 0 ค่า tpr และ fpr จึง 0 ทั้งคู่
แต่ถ้าให้จุดแบ่งเป็น 1 ผลที่ทายจะเป็นบวกหมด แบบนั้นทั้งค่าลบจริงและลบปลอมก็จะมีอยู่ 0 แบบนั้น tpr=บวกจริง(บวกจริง+0)=1, fpr = ลบจริง(ลบจริง+0)=1
หากดูเส้นกราฟนี้แล้ว จะสามารถพิจารณาได้ว่าผลการทำนายของเรานั้นดีแค่ไหน
โดยทั่วไปจะถือว่าหากกราฟยิ่งชิดด้านบนมากก็ยิ่งแปลว่าทำนายได้ดี แต่หากกราฟเป็นเส้นตรงจะแสดงว่าไม่ดี
กราฟชิดด้านบนมากหมายความว่าพื้นที่ใต้กราฟมาก ค่าพื้นที่ใต้กราฟ ROC นี้ถูกเรียกว่า AUC (area under curve) เป็นค่าหนึ่งที่ใช้วัด
เส้นกราฟ ROC อาจเป็นดังภาพนี้
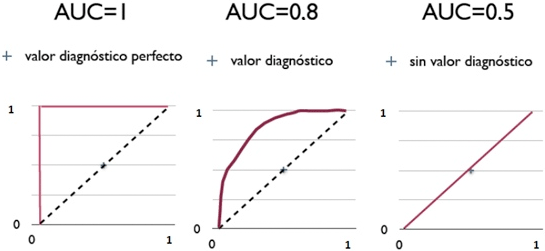
(ที่มาของภาพ http://blog.csdn.net/pipisorry/article/details/51788927)
หากกราฟชิดซ้ายบนแบบในภาพซ้ายค่าพื้นที่ใต้กราฟก็จะเป็น 1 นั่นคือสภาพในอุดมคติ แต่ในความเป็นจริงแค่โค้งค่อนไปบนซ้ายหน่อยก็ถือว่าดีแล้ว เช่นภาพกลาง ถือว่าทายถูกเยอะ
ส่วนถ้ากราฟออกมาเกือบตรงแบบภาพขวาพื้นที่ใต้กราฟก็จะเป็น 0.5 แบบนั้นคือทำนายอะไรแทบไม่ได้ คือมีผิดถูกพอๆกัน
แต่ถ้าหากกราฟออกมาค่อนไปทางขวาล่าง แบบนั้นค่าพื้นที่ใต้กราฟจะต่ำกว่า 0.5 กรณีแบบนี้ไม่ใช่ว่าผลการทำนายแย่ แต่หมายความว่าผลการทายมีแต่ผิดเต็มไปหมด
การที่ทายผลออกมาได้ผิดเยอะนั้นหากมองในมุมกลับก็ถือว่าต้องยอดเยี่ยม เพราะการจะทายอะไรให้ผิดได้ตลอดแสดงว่าต้องรู้คำตอบแต่จงใจตอบให้ผิด
ดังนั้นแค่พลิกผลการทายจากบวกเป็นลบ ก็จะกลายเป็นว่าทายถูกเยอะทันที
เคยมีกรณีที่นักสืบสอบสวนคดีโดยแกล้งถามคำถามที่เกี่ยวข้องกับคดีให้คนร้ายตอบ ปรากฏว่าคนร้ายจงใจตอบให้ผิดหมด นั่นเท่ากับคนร้ายติดกับดักเข้าเต็มเปา เพราะถ้าไม่รู้อะไรเลยก็จะไม่มีทางตอบให้ผิดหมดได้ ต้องมีถูกบ้างผิดบ้าง ดังนั้นจึงโดนจับได้ทันที
การหาพื้นที่ใต้กราฟก็คือการหาปริพันธ์ (integrate) นั่นเอง ซึ่งเราก็อาจจะเขียนโค้ดเพื่อคำนวณเองก็ได้ แต่ในที่นี้จะใช้ฟังก์ชันที่มีอยู่แล้วของ sklearn
ผลที่ได้เข้าใกล้ 1 แสดงว่าทำนายออกมาได้ดีมาก
หรือถ้าไม่ได้คำนวนค่า fpr และ tpr มาแล้วตั้งแต่ต้น sklearn ก็มีคำสั่งที่ใช้หาค่า AUC ได้ทันที
ผลที่ได้จะออกมาต่างกันเล็กน้อยเนื่องจากตอนที่เราคำนวณค่า fpr และ tpr ตอนแรกได้แบ่งกราฟเป็นแค่ 10 ช่วง (11 จุด) ความละเอียดในการคำนวณค่อนข้างต่ำ แต่ในฟังก์ชันที่คำนวณให้เองนี้จะคำนวณละเอียดกว่า ค่าที่ได้จึงมีความแม่นยำมากกว่า
ถ้าแค่ต้องการ fpr กับ tpr เพื่อไปคำนวณ auc เองทีหลัง sklearn ก็มีคำสั่งนั้นให้เช่นกัน
ต่อมาทีนี้หากเราลองแกล้งเปลี่ยนค่าน้ำหนักและไบแอสของตัวทำนายของเราให้ผลการทำนายออกมาเปลี่ยนไปจะเป็นยังไง
เช่นลองปรับค่า
แก้ค่าเป็นแบบนี้แล้วก็รันโค้ดเดิมเพื่อวาดภาพแบบเดิมใหม่ก็จะได้ภาพแบบนี้
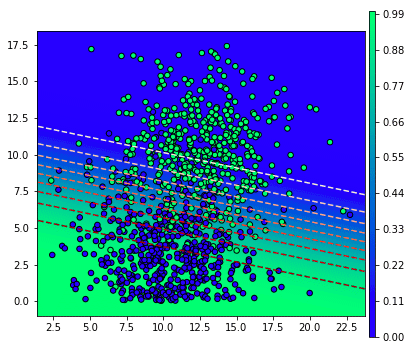
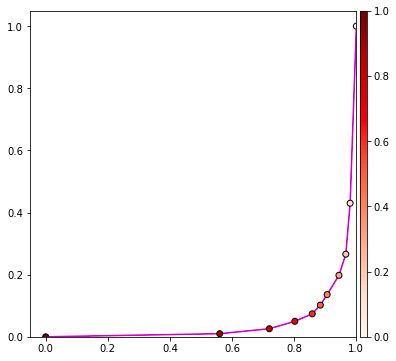
เส้นแบ่งจะเหมือนเดิมแต่ว่าสีเป็นตรงกันข้าม
ส่วนกราฟ ROC จะออกมาชิดขวาล่าง หมายความว่าผลการทายเลี่ยงคำตอบถูกได้อย่างยอดเยี่ยม
และค่าพื้นที่ใต้กราฟที่ได้ก็คือ 0.043084
หรือถ้าลองเปลี่ยนไปคนละทางกันเลยให้ผลการทำนายออกมาไม่แม่น เช่นลองปรับเป็นค่านี้
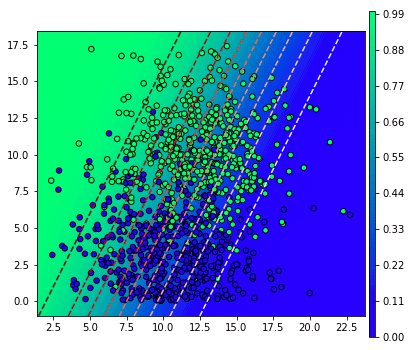
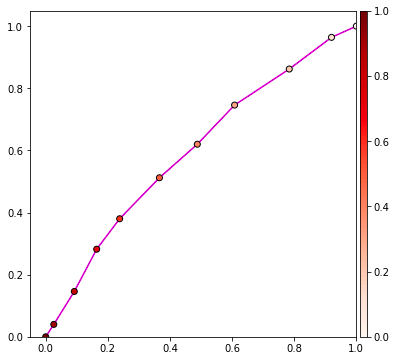
เส้นแบ่งจะวางไปคนละแนวกับที่ควรเลย ทำให้ไม่สามารถแบ่งแยกคำตอบได้ จึงออกมาถูกผิดครึ่งๆ
ส่วนกราฟ ROC ก็แทบจะเป็นเส้นตรง
แล้วพอคำนวณพื้นที่ใต้กราฟก็จะออกมาเป็น 0.598972 นั่นคือผลค่อนข้างแย่
โดยสรุปแล้ว ROC สามารถใช้ประเมินประสิทธิภาพของแบบจำลองการเรียนรู้ของเครื่องได้เช่นเดียวกับค่าความแม่นยำหรือคะแนน f1 เพียงแต่ว่า ROC ใช้วิเคราะห์ปัญหาที่มีแค่ ๒ คำตอบ (บวกหรือลบ) เท่านั้น
อ้างอิง
นอกจากนี้แล้วก็ยังมีอีกวิธีหนึ่งในการพิจารณาประสิทธิภาพของแบบจำลองที่ใช้ทำนาย นั่นคือการดูกราฟ ROC (Receiver operating characteristic)
การจะอธิบายว่า ROC คืออะไรนั้นหากเริ่มจากอธิบายเป็นคำพูดเลยคงจะยาก ดังนั้นขอเริ่มด้วยการยกตัวอย่าง
สมมุติว่าข้อมูลการตรวจโรคจากสารในร่างกายของคน 1000 คนออกมาเป็นดังนี้ โดยแกนนอนคือปริมาณสาร a แกนนอนคือปริมาณสาร b สีเขียวคือผลบวก (มีโรค) สีน้ำเงินคือผลลบ (ไม่มีโรค)

โค้ดสำหรับสร้างข้อมูลและวาดภาพเขียนได้ดังนี้
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=2,cluster_std=3,center_box=[3,20],random_state=2)
X = np.abs(X)
plt.figure(figsize=[7,6])
plt.axes(aspect=1)
plt.xlabel('ปริมาณสาร a',family='Tahoma')
plt.ylabel('ปริมาณสาร b',family='Tahoma')
plt.scatter(X[:,0],X[:,1],c=z,s=30,alpha=0.5,edgecolor='k',cmap='winter')
plt.show()จากนั้นเราอาจใช้ LogisticRegression ของ sklearn เพื่อหาจุดแบ่งในการทำนายว่าถ้าตรวจพบคนไข้ที่มีปริมาณสาร a และสาร b เท่านี้จะสรุปว่าเป็นโรคหรือไม่
เราสามารถคำนวณความน่าจะเป็นของการเกิดผลบวกในแต่ละบริเวณได้โดยใช้เมธอด .predict_proba แบบนี้
from sklearn.linear_model import LogisticRegression as Lori
lori = Lori()
lori.fit(X,z)
mX = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,101),np.linspace(-1,X[:,1].max()+1,101))
mX = np.stack(mX,2)
mz = lori.predict_proba(mX.reshape(-1,2))[:,1].reshape(101,101)
plt.figure(figsize=[7,6])
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,s=30,edgecolor='k',cmap='winter')
plt.contourf(mX[:,:,0],mX[:,:,1],mz,100,vmin=0,vmax=1,alpha=0.5,cmap='winter',zorder=0)
plt.colorbar(pad=0.01,aspect=50)
plt.show()
จากผลที่ได้ตรงนี้ ปกติแล้วเวลาตัดสินว่าผลเป็นบวกหรือเปล่าก็จะดูว่าความเป็นไปได้ถึง 0.5 หรือไม่ กล่าวคือ ขีดเส้นประสีแดงคั่นแบบนี้
proba = lori.predict_proba(X)[:,1]
threshold = 0.5
ox = (proba>threshold)==z
plt.figure(figsize=[7,6])
plt.axes(aspect=1)
plt.scatter(X[ox,0],X[ox,1],c=z[ox],s=30,edgecolor='k',cmap='winter')
plt.scatter(X[~ox,0],X[~ox,1],c=z[~ox],s=30,edgecolor='r',cmap='winter')
plt.contour(mX[:,:,0],mX[:,:,1],mz>threshold,1,vmin=0,vmax=1,linestyles='--',colors='r')
plt.contourf(mX[:,:,0],mX[:,:,1],mz,100,vmin=0,vmax=1,alpha=0.5,cmap='winter',zorder=0)
plt.colorbar(pad=0.01,aspect=50)
plt.show()
จุดที่ถูกล้อมกรอบสีแดงคือส่วนที่ถูกจำแนกผิด
อย่างไรก็ตาม หากเราลองปรับเปลี่ยนว่าให้ผลความน่าจะเป็นเป็น 0.8 จึงจะตัดสินว่าเป็นผลบวก จะเป็นแบบนี้ (ลองแก้ threshlod เป็น 0.8 แล้ววาดใหม่)

จะเห็นว่าผลที่ถูกทายว่าเป็นผลบวกมีน้อยลง
ส่วนทางกลับกันหากลองปรับให้เป็น 0.2 เส้นแบ่งก็จะเลื่อนลงมาด้านล่าง

การเปลี่ยนค่าจุดแบ่งนี้มีผลทำให้อัตราผลบวกจริง (true positive rate, tpr) และอัตราผลบวกปลอม (false positive rate, fpr) มีค่าเปลี่ยนแปลงไป
อัตราผลบวกจริง ก็คือค่าความระลึก (recall) ซึ่งกล่าวถึงไปในบทความก่อน คำนวณได้จาก
อัตราผลบวกจริง = บวกจริง/(บวกจริง+ลบปลอม)
ส่วนอัตราผลบวกปลอม คำนวณได้จาก
อัตราผลบวกปลอม = บวกปลอม/(บวกปลอม+ลบจริง)
ค่าทั้งสองนี้อาจคำนวณได้ดังนี้
t = proba>threshold
tpr = (z==t).T[z==1].mean()
fpr = (z!=t).T[z==0].mean()threshold คือจุดแบ่ง อาจมีค่าตั้งแต่ 0 จนถึง 1 ค่าจุดแบ่งมีผลต่อค่า tpr และ fpr
แล้วถ้าหากเราลองทำการวาดกราฟที่แสดงความสัมพันธ์ระหว่างค่าจุดแบ่ง โดยเขียนตามนี้
mX = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,101),np.linspace(-1,X[:,1].max()+1,101))
mX = np.stack(mX,2)
mz = lori.predict_proba(mX.reshape(-1,2))[:,1].reshape(101,101)
proba = lori.predict_proba(X)[:,1]
plt.figure(figsize=[7,6])
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,s=30,edgecolor='k',cmap='winter')
plt.contour(mX[:,:,0],mX[:,:,1],mz,np.linspace(0,1,11),vmin=0,vmax=1,levels=np.linspace(0,1,11),linestyles='--',cmap='Reds')
plt.contourf(mX[:,:,0],mX[:,:,1],mz,100,vmin=0,vmax=1,cmap='winter',zorder=0)
plt.colorbar(pad=0.01,aspect=50)
plt.show()
proba = lori.predict_proba(X)[:,1]
t = proba>np.linspace(0,1,11)[:,None]
tpr = (z==t).T[z==1].mean(0)
fpr = (z!=t).T[z==0].mean(0)
plt.figure(figsize=[7,6])
plt.axes(aspect=1,xlim=[-0.05,1],ylim=[0,1.05])
plt.plot(fpr,tpr,'m',zorder=0)
plt.scatter(fpr,tpr,c=np.linspace(0,1,11),edgecolor='k',cmap='Reds')
plt.colorbar(pad=0.01,aspect=50)
plt.show()ก็จะได้แบบนี้


ในที่นี้สีของจุดในกราฟจะตรงกับสีของเส้นแบ่งในแผนภาพด้านบน
เส้นกราฟนี้ล่ะที่เรียกว่าเส้นกราฟ ROC
เส้นกราฟจะเริ่มจาก (0,0) และจบที่ (1,1) เสมอ เพราะถ้าให้ค่าจุดแบ่งเป็น 0 หมายความว่าผลที่ทายจะเป็นลบหมด ดังนั้นไม่ว่าบวกจริงหรือบวกปลอมก็จะมีอยู่ 0 ค่า tpr และ fpr จึง 0 ทั้งคู่
แต่ถ้าให้จุดแบ่งเป็น 1 ผลที่ทายจะเป็นบวกหมด แบบนั้นทั้งค่าลบจริงและลบปลอมก็จะมีอยู่ 0 แบบนั้น tpr=บวกจริง(บวกจริง+0)=1, fpr = ลบจริง(ลบจริง+0)=1
หากดูเส้นกราฟนี้แล้ว จะสามารถพิจารณาได้ว่าผลการทำนายของเรานั้นดีแค่ไหน
โดยทั่วไปจะถือว่าหากกราฟยิ่งชิดด้านบนมากก็ยิ่งแปลว่าทำนายได้ดี แต่หากกราฟเป็นเส้นตรงจะแสดงว่าไม่ดี
กราฟชิดด้านบนมากหมายความว่าพื้นที่ใต้กราฟมาก ค่าพื้นที่ใต้กราฟ ROC นี้ถูกเรียกว่า AUC (area under curve) เป็นค่าหนึ่งที่ใช้วัด
เส้นกราฟ ROC อาจเป็นดังภาพนี้

(ที่มาของภาพ http://blog.csdn.net/pipisorry/article/details/51788927)
หากกราฟชิดซ้ายบนแบบในภาพซ้ายค่าพื้นที่ใต้กราฟก็จะเป็น 1 นั่นคือสภาพในอุดมคติ แต่ในความเป็นจริงแค่โค้งค่อนไปบนซ้ายหน่อยก็ถือว่าดีแล้ว เช่นภาพกลาง ถือว่าทายถูกเยอะ
ส่วนถ้ากราฟออกมาเกือบตรงแบบภาพขวาพื้นที่ใต้กราฟก็จะเป็น 0.5 แบบนั้นคือทำนายอะไรแทบไม่ได้ คือมีผิดถูกพอๆกัน
แต่ถ้าหากกราฟออกมาค่อนไปทางขวาล่าง แบบนั้นค่าพื้นที่ใต้กราฟจะต่ำกว่า 0.5 กรณีแบบนี้ไม่ใช่ว่าผลการทำนายแย่ แต่หมายความว่าผลการทายมีแต่ผิดเต็มไปหมด
การที่ทายผลออกมาได้ผิดเยอะนั้นหากมองในมุมกลับก็ถือว่าต้องยอดเยี่ยม เพราะการจะทายอะไรให้ผิดได้ตลอดแสดงว่าต้องรู้คำตอบแต่จงใจตอบให้ผิด
ดังนั้นแค่พลิกผลการทายจากบวกเป็นลบ ก็จะกลายเป็นว่าทายถูกเยอะทันที
เคยมีกรณีที่นักสืบสอบสวนคดีโดยแกล้งถามคำถามที่เกี่ยวข้องกับคดีให้คนร้ายตอบ ปรากฏว่าคนร้ายจงใจตอบให้ผิดหมด นั่นเท่ากับคนร้ายติดกับดักเข้าเต็มเปา เพราะถ้าไม่รู้อะไรเลยก็จะไม่มีทางตอบให้ผิดหมดได้ ต้องมีถูกบ้างผิดบ้าง ดังนั้นจึงโดนจับได้ทันที
การหาพื้นที่ใต้กราฟก็คือการหาปริพันธ์ (integrate) นั่นเอง ซึ่งเราก็อาจจะเขียนโค้ดเพื่อคำนวณเองก็ได้ แต่ในที่นี้จะใช้ฟังก์ชันที่มีอยู่แล้วของ sklearn
from sklearn.metrics import auc
print(auc(fpr,tpr)) # ได้ 0.952204ผลที่ได้เข้าใกล้ 1 แสดงว่าทำนายออกมาได้ดีมาก
หรือถ้าไม่ได้คำนวนค่า fpr และ tpr มาแล้วตั้งแต่ต้น sklearn ก็มีคำสั่งที่ใช้หาค่า AUC ได้ทันที
from sklearn.metrics import roc_auc_score
print(roc_auc_score(z,proba)) # 0.956916ผลที่ได้จะออกมาต่างกันเล็กน้อยเนื่องจากตอนที่เราคำนวณค่า fpr และ tpr ตอนแรกได้แบ่งกราฟเป็นแค่ 10 ช่วง (11 จุด) ความละเอียดในการคำนวณค่อนข้างต่ำ แต่ในฟังก์ชันที่คำนวณให้เองนี้จะคำนวณละเอียดกว่า ค่าที่ได้จึงมีความแม่นยำมากกว่า
ถ้าแค่ต้องการ fpr กับ tpr เพื่อไปคำนวณ auc เองทีหลัง sklearn ก็มีคำสั่งนั้นให้เช่นกัน
from sklearn.metrics import roc_curve
fpr,tpr,threshold = roc_curve(z,proba)ต่อมาทีนี้หากเราลองแกล้งเปลี่ยนค่าน้ำหนักและไบแอสของตัวทำนายของเราให้ผลการทำนายออกมาเปลี่ยนไปจะเป็นยังไง
เช่นลองปรับค่า
lori.coef_ = -lori.coef_
lori.intercept_ = -lori.intercept_แก้ค่าเป็นแบบนี้แล้วก็รันโค้ดเดิมเพื่อวาดภาพแบบเดิมใหม่ก็จะได้ภาพแบบนี้


เส้นแบ่งจะเหมือนเดิมแต่ว่าสีเป็นตรงกันข้าม
ส่วนกราฟ ROC จะออกมาชิดขวาล่าง หมายความว่าผลการทายเลี่ยงคำตอบถูกได้อย่างยอดเยี่ยม
และค่าพื้นที่ใต้กราฟที่ได้ก็คือ 0.043084
หรือถ้าลองเปลี่ยนไปคนละทางกันเลยให้ผลการทำนายออกมาไม่แม่น เช่นลองปรับเป็นค่านี้
lori.coef_ = np.array([[-0.4,0.2]])
lori.intercept_ = np.array([3])

เส้นแบ่งจะวางไปคนละแนวกับที่ควรเลย ทำให้ไม่สามารถแบ่งแยกคำตอบได้ จึงออกมาถูกผิดครึ่งๆ
ส่วนกราฟ ROC ก็แทบจะเป็นเส้นตรง
แล้วพอคำนวณพื้นที่ใต้กราฟก็จะออกมาเป็น 0.598972 นั่นคือผลค่อนข้างแย่
โดยสรุปแล้ว ROC สามารถใช้ประเมินประสิทธิภาพของแบบจำลองการเรียนรู้ของเครื่องได้เช่นเดียวกับค่าความแม่นยำหรือคะแนน f1 เพียงแต่ว่า ROC ใช้วิเคราะห์ปัญหาที่มีแค่ ๒ คำตอบ (บวกหรือลบ) เท่านั้น
อ้างอิง
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
http://www.gss.com.tw/index.php/focus/eis/157-eis82/1540-eis82-2
https://www.zhihu.com/question/30643044
http://blog.csdn.net/pipisorry/article/details/51788927
https://qiita.com/kenmatsu4/items/0a862a42ceb178ba7155
http://www.gss.com.tw/index.php/focus/eis/157-eis82/1540-eis82-2
https://www.zhihu.com/question/30643044
http://blog.csdn.net/pipisorry/article/details/51788927
https://qiita.com/kenmatsu4/items/0a862a42ceb178ba7155
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn