[python] ผลบวกลบจริงปลอม, ความเที่ยงและความระลึกได้, ค่าคะแนน f1
เขียนเมื่อ 2017/10/14 20:14
แก้ไขล่าสุด 2022/07/21 15:13
ปกติแล้วเวลาที่เราทายอะไรสักอย่าง การที่ดูผลแล้วบอกประสิทธิภาพการทายว่าทายดีแค่ไหนนั้น มักจะคิดง่ายๆว่าเอาจำนวนที่ทายถูกหารด้วยจำนวนทั้งหมด คิดดูว่าเป็นสัดส่วนเท่าไหร่
นั่นคือการคำนวณความแม่นยำ (accuracy) ซึ่งเป็นการคำนวณพื้นฐานที่ใช้กันบ่อยทั่วไปมากที่สุด
แต่ว่าในทางสถิติแล้ว บางครั้งก็มีการใช้วิธีการคำนวณอย่างอื่นเพื่อให้คะแนนการทาย ซึ่งในบางกรณีก็อาจจะเหมาะมากกว่า
ในบทความนี้เราจะมาพูดถึงสิ่งที่เรียกว่า ความเที่ยง (precision) ความระลึกได้ (recall) และคะแนน f1
ปกติแล้ว ในการพิจารณาปัญหาซึ่งต้องทำนายผลที่มีคำตอบอยู่แค่ ๒ ตัวเลือก เราอาจเรียกผลการทำนาย ๒ แบบนั้นว่าเป็นผลบวกกับผลลบ
ผลบวกมักหมายถึงตรวจเจอสิ่งที่ต้องการหา ผลลบคือไม่เจอสิ่งที่กำลังตรวจหาอยู่
คำว่าบวกลบในที่นี้ไม่ได้หมายความว่าบวกจะต้องดี ลบจะต้องไม่ดี เช่นหากเราต้องการตรวจว่าคนคนหนึ่งเป็นโรคหรือเปล่า ผลบวกก็คือเป็นโรค ผลลบก็คือไม่เป็นโรค
บางทีบวกลบจะเป็นอะไรก็ได้ ไม่ได้ต้องตัดสินชัดเจนแน่นอน แต่โดยทั่วไปแล้วขึ้นอยู่กับว่าจะเน้นมองไปที่อะไรเป็นหลัก
เช่นหากเราต้องการพิจารณาคนกลุ่มหนึ่งซึ่งกำลังสนทนากันในเน็ต แล้วอยากจะหาว่าคนไหนเป็นผู้หญิง งั้นผลบวกก็คือเป็นผู้หญิง ผลลบคือผู้ชาย
ทีนี้เมื่อมีการทายเกิดขึ้น แล้วมีการเฉลยผลที่ถูกต้องจริงๆ พอเปรียบเทียบผลการทายกับผลเฉลยจริงเราอาจแบ่งผลลัพธ์ได้เป็น ๔ ดังตารางนี้
- บวกจริง (true positive, TP) ทายว่าเป็นบวกแล้วก็เป็นบวกจริงๆ
- บวกปลอม (false positive, FP) ทายว่าเป็นบวกแต่ดันเป็นลบ
- ลบปลอม (false negative, FN) ทายว่าเป็นลบแต่ดันเป็นบวก
- ลบจริง (true negative, TN) ทายว่าเป็นลบแล้วก็เป็นลบจริงๆ
และเมื่อจะหาค่าความแม่นยำ ก็คือเอาผลที่เป็นจริง ไม่ว่าจะเป็นบวกหรือลบก็ตาม มาหารด้วยทั้งหมด กล่าวคือ
ความแม่นยำ = (บวกจริง+ลบจริง)/(บวกจริง+บวกปลอม+ลบปลอม+ลบจริง)
แต่นอกจากนี้ยังมีวิธีการพิจารณาโดยพิจารณาเฉพาะผลที่ทายได้เป็นบวก ดูว่าที่ทายมานั้นเป็นบวกจริงสักเท่าไหร่ นั่นจะเรียกว่า ความเที่ยง
ความเที่ยง = บวกจริง/(บวกจริง+บวกปลอม)
ค่านี้จะบอกให้รู้ว่าที่ทายว่าเป็นบวกนั้นน่าเชื่อถือแค่ไหน เช่นถ้าคนไข้ถูกตรวจว่าเป็นโรคขึ้นมา เขาจะมีโอกาสเป็นโรคจริงๆแค่ไหน
นอกจากนี้ก็มีอีกค่า ซึ่งพิจารณาเฉพาะของที่จริงๆแล้วเป็นบวก เราจะตรวจพบว่ามันเป็นบวกได้จริงๆแค่ไหน ค่านั้นเรียกว่า ความระลึกได้
ความระลึกได้ = บวกจริง/(บวกจริง+ลบปลอม)
เช่น ถ้าเรากำลังตรวจหาโรคบางอย่างอยู่ ค่านี้จะบอกว่าเรามีโอกาสตรวจเจอมันแค่ไหน
ลบปลอม ก็หมายความว่าจริงๆเป็นบวก แต่กลับถูกตรวจว่าเป็นลบ คือหาไม่เจอ พลาดสิ่งที่ต้องการตรวจเจอไป
บ่อยครั้งที่ค่าความเที่ยงกับค่าความระลึกได้นั้นสวนทางกัน
ยกตัวอย่างเช่น เราค้นหาเว็บที่ต้องการในกูเกิล ยิ่งผลการค้นหาออกมามากก็มีโอกาสที่ของที่ต้องการจะอยู่ในนั้นมาก แต่ของที่ไม่จำเป็นก็โผล่ออกมาเยอะตาม
นั่นก็คือ ถ้าแค่เข้าข่ายสักหน่อยก็ตัดสินว่าใช่แล้ว ความระลึกได้จะสูง แต่ความเที่ยงจะต่ำ เพราะหาเจอสิ่งที่ต้องการได้มาก แต่ก็มีสิ่งที่ไม่ใช่โผล่มาเพิ่ม
แต่ถ้าต้องรอให้มั่นใจมากๆจึงจะตัดสินใจว่าใช่ ความเที่ยงจะสูง แต่ความระลึกได้จะสูง เพราะสิ่งที่หาได้ส่วนใหญ่ใช่หมด แต่ก็ตกหล่นของที่ควรจะหาได้ไปอีกเยอะ
ค่าไหนจะสำคัญมากหรือน้อยกว่าก็อาจขึ้นกับกรณี เช่นถ้าเป็นการตรวจหาโรคละก็ กรณีนี้การตรวจให้เจอโรคจะสำคัญ ดังนั้นความระลึกได้ควรจะต้องสูง
ถ้ามีใครที่เป็นโรคแต่กลับตัดสินว่าไม่เป็น แบบนั้นอันตราย แต่ถ้าคนที่ไม่เป็นแต่ถูกตัดสินว่าเป็น แบบนั้นอาจไม่เสียหายเท่า ดังนั้นกรณีแบบนี้ถ้าให้ผลเป็นบวกง่ายไว้จะดีกว่า
เมื่อนำความเที่ยงกับความระลึกได้มาเฉลี่ยกันก็จะได้เป็นค่าที่เรียกว่าคะแนน f1
เพียงแต่ว่าไม่ใช่การเฉลี่ยโดยตรง แต่เป็นการเฉลี่ยส่วนกลับ เหมือนเวลาบวกความต่างศักย์ของถ่านที่ต่อกันแบบขนาน แบบนี้เรียกว่าค่าเฉลี่ยฮาร์มอนิก
กล่าวคือ
1/f1 = 0.5×(1/ความเที่ยง + 1/ความระลึกได้)
หรือจะคำนวณได้ว่า
f1 = 2×บวกจริง/(2×บวกจริง+บวกปลอม+ลบปลอม)
= 2×จำนวนที่ทายว่าเป็นบวกและเป็นบวกจริง/(จำนวนที่ทายว่าเป็นบวก+จำนวนที่ผลจริงๆเป็นบวก)
เราอาจสร้างฟังก์ชันคำนวณค่าต่างๆเหล่านี้ในไพธอนได้โดย
นอกจากนี้ใน sklearn ก็ได้มีเตรียมฟังก์ชันพวกนี้ไว้อยู่แล้ว จะนำมาใช้ก็ได้เช่นกัน
ลองยกตัวอย่าง เช่น ใช้เครื่องตรวจอาการป่วยวินิจฉัยโรคให้ผู้ป่วย ๑๐ คนโดยในนั้นมีผู้ป่วยจริงๆอยู่ ๓ คน
แต่ว่าอุปกรณ์วัดที่ใช้มีอยู่หลายตัว ให้ผลวินิยฉัยต่างกันไป เมื่อนำมาเปรียบเทียบกับค่าจริง ผลคะแนนที่ได้ออกมาเป็นดังนี้
ผลที่ได้
อันที่ 2 ทายแม่นเท่าอันที่ 1 แต่กลับได้คะแนน f1 เยอะกว่า
ส่วนอันที่ 3 กับ 4 ทายแม่นน้อยกว่าอันที่ 1 เยอะแต่กลับได้ค่า f1 เท่ากัน
ดังนั้นจะเห็นได้ว่าในบางกรณีคะแนนที่พิจารณาจาก f1 จะต่างจากค่าความแม่นยำ ดังนั้นการเลือกว่าจะให้คะแนนด้วยวิธีไหนจึงเห็นผลได้ชัด
คะแนน f1 ยังอาจใช้เพื่อพิจารณาปัญหาการแบ่งกลุ่มเป็นหลายกลุ่มได้ด้วย เพียงแต่ว่ากรณีนี้จะมีความคลุมเครือ เพราะถ้ามีแค่ ๒ เราจะแบ่งให้ผลอันหนึ่งเป็นบวก และอีกอันเป็นลบ
แต่เมื่อมีหลายกลุ่มอาจทำได้โดยการพิจารณาว่าให้ตัวหนึ่งเป็นบวกที่เหลือเป็นลบ แล้วก็คำนวณค่าความเที่ยงกับความระลึกได้ไปทีนึง จากนั้นก็เปลี่ยนให้อีกตัวเป็นบวกแทน แล้วก็คำนวณใหม่ ไล่ไปให้ทุกตัวได้ถูกพิจารณาเป็นบวกทั้งหมด สุดท้ายก็เอาผลที่ได้ของแต่ละรอบมาเฉลี่ยกัน
เพียงแต่ว่าการเฉลี่ยนั้นอาจเฉลี่ยโดยคิดน้ำหนักตามจำนวนผลที่แต่ละกลุ่มมี ก็จะได้คำตอบต่างกันออกไป
กรณีที่เฉลี่ยทุกกลุ่มด้วยน้ำหนักเท่ากันอาจลองเขียนฟังก์ชันได้ดังนี้
ส่วนฟังก์ชัน f1_score ของ sklearn นั้นโดยทั่วไปแล้วหากเราป้อนค่าที่ไม่ใช่มีแค่ ๒ กลุ่ม (ไม่ได้มีแค่ 0,1) จำเป็นจะต้องระบุด้วยว่าจะเฉลี่ยแบบไหน
หากต้องการเฉลี่ยให้เท่ากันก็ใส่เป็น average='macro' แต่ถ้าต้องการถ่วงน้ำหนักให้ใส่ average='weighted'
ตัวอย่าง
weighted จะได้เยอะกว่า macro เพราะค่า 1 ซึ่งทายถูกหมดนั้นมีจำนวนมาก หากเฉลี่ยโดยถ่วงน้ำหนักคะแนนก็ย่อมสูง แต่ถ้าไม่ถ่วงน้ำหนักก็จะโดนคะแนนของเลข 0 และ 2 ซึ่งทายผิดเยอะดึงลง
ต่อมาลองเอามาใช้ในการวิเคราะห์ผลของปัญหาการวิเคราะห์การถดถอยโลจิสติกดู
สมมุติว่าข้อมูลการตรวจโรคจากสารในร่างกายของคน 1000 คนออกมาเป็นดังนี้ โดยแกนนอนคือปริมาณสาร a แกนนอนคือปริมาณสาร b ส่วนสีของจุดบ่งบอกถึงผล โดยสีเขียวคือผลบวก (มีโรค) สีน้ำเงินคือผลลบ (ไม่มีโรค)
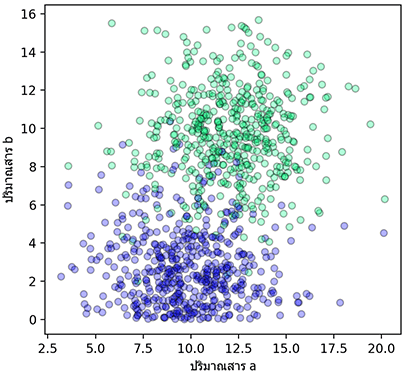
ข้อมูลถูกสร้างโดยโค้ดตามนี้
จากนั้นลองหาพารามิเตอร์ค่าน้ำหนักและไบแอสโดยใช้ LogisticRegression ของ sklearn เพื่อหาเส้นแบ่ง
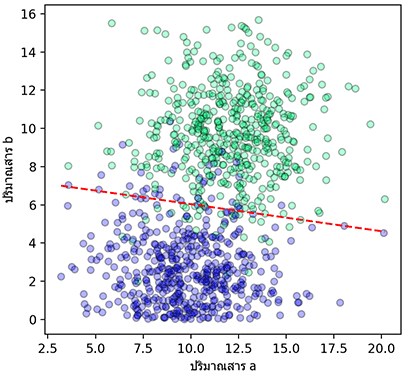
ลองเอาผลการแบ่งนี้มาใช้ทำนายผลของข้อมูลชุดนี้
ได้
แต่ว่าหากลองปรับไบแอสให้เส้นเลื่อนขึ้นบนไปสักหน่อย โดยที่น้ำหนักเหมือนเดิม
เส้นก็จะเปลี่ยนไปตามนี้
แล้วผลที่ได้ก็จะกลายเป็น
ในทางตรงกันข้ามหากปรับไบแอสให้เส้นเลื่อนขึ้นบน
นั่นคือความระลึกได้จะเพิ่มขึ้น แต่ความเที่ยงจะลดลง หมายความว่าหาผลบวกที่ต้องการได้เกือบหมด แต่ก็มีที่ไม่ใช่ปนมาด้วยเยอะ
อ้างอิง
นั่นคือการคำนวณความแม่นยำ (accuracy) ซึ่งเป็นการคำนวณพื้นฐานที่ใช้กันบ่อยทั่วไปมากที่สุด
แต่ว่าในทางสถิติแล้ว บางครั้งก็มีการใช้วิธีการคำนวณอย่างอื่นเพื่อให้คะแนนการทาย ซึ่งในบางกรณีก็อาจจะเหมาะมากกว่า
ในบทความนี้เราจะมาพูดถึงสิ่งที่เรียกว่า ความเที่ยง (precision) ความระลึกได้ (recall) และคะแนน f1
ปกติแล้ว ในการพิจารณาปัญหาซึ่งต้องทำนายผลที่มีคำตอบอยู่แค่ ๒ ตัวเลือก เราอาจเรียกผลการทำนาย ๒ แบบนั้นว่าเป็นผลบวกกับผลลบ
ผลบวกมักหมายถึงตรวจเจอสิ่งที่ต้องการหา ผลลบคือไม่เจอสิ่งที่กำลังตรวจหาอยู่
คำว่าบวกลบในที่นี้ไม่ได้หมายความว่าบวกจะต้องดี ลบจะต้องไม่ดี เช่นหากเราต้องการตรวจว่าคนคนหนึ่งเป็นโรคหรือเปล่า ผลบวกก็คือเป็นโรค ผลลบก็คือไม่เป็นโรค
บางทีบวกลบจะเป็นอะไรก็ได้ ไม่ได้ต้องตัดสินชัดเจนแน่นอน แต่โดยทั่วไปแล้วขึ้นอยู่กับว่าจะเน้นมองไปที่อะไรเป็นหลัก
เช่นหากเราต้องการพิจารณาคนกลุ่มหนึ่งซึ่งกำลังสนทนากันในเน็ต แล้วอยากจะหาว่าคนไหนเป็นผู้หญิง งั้นผลบวกก็คือเป็นผู้หญิง ผลลบคือผู้ชาย
ทีนี้เมื่อมีการทายเกิดขึ้น แล้วมีการเฉลยผลที่ถูกต้องจริงๆ พอเปรียบเทียบผลการทายกับผลเฉลยจริงเราอาจแบ่งผลลัพธ์ได้เป็น ๔ ดังตารางนี้
| /人◕ ‿‿ ◕人\ | ค่าจริง | ||
| บวก | ลบ | ||
| ค่าทาย | บวก | บวกจริง TP |
บวกปลอม FP |
| ลบ | ลบปลอม FN |
ลบจริง TN |
|
- บวกจริง (true positive, TP) ทายว่าเป็นบวกแล้วก็เป็นบวกจริงๆ
- บวกปลอม (false positive, FP) ทายว่าเป็นบวกแต่ดันเป็นลบ
- ลบปลอม (false negative, FN) ทายว่าเป็นลบแต่ดันเป็นบวก
- ลบจริง (true negative, TN) ทายว่าเป็นลบแล้วก็เป็นลบจริงๆ
และเมื่อจะหาค่าความแม่นยำ ก็คือเอาผลที่เป็นจริง ไม่ว่าจะเป็นบวกหรือลบก็ตาม มาหารด้วยทั้งหมด กล่าวคือ
ความแม่นยำ = (บวกจริง+ลบจริง)/(บวกจริง+บวกปลอม+ลบปลอม+ลบจริง)
แต่นอกจากนี้ยังมีวิธีการพิจารณาโดยพิจารณาเฉพาะผลที่ทายได้เป็นบวก ดูว่าที่ทายมานั้นเป็นบวกจริงสักเท่าไหร่ นั่นจะเรียกว่า ความเที่ยง
ความเที่ยง = บวกจริง/(บวกจริง+บวกปลอม)
ค่านี้จะบอกให้รู้ว่าที่ทายว่าเป็นบวกนั้นน่าเชื่อถือแค่ไหน เช่นถ้าคนไข้ถูกตรวจว่าเป็นโรคขึ้นมา เขาจะมีโอกาสเป็นโรคจริงๆแค่ไหน
นอกจากนี้ก็มีอีกค่า ซึ่งพิจารณาเฉพาะของที่จริงๆแล้วเป็นบวก เราจะตรวจพบว่ามันเป็นบวกได้จริงๆแค่ไหน ค่านั้นเรียกว่า ความระลึกได้
ความระลึกได้ = บวกจริง/(บวกจริง+ลบปลอม)
เช่น ถ้าเรากำลังตรวจหาโรคบางอย่างอยู่ ค่านี้จะบอกว่าเรามีโอกาสตรวจเจอมันแค่ไหน
ลบปลอม ก็หมายความว่าจริงๆเป็นบวก แต่กลับถูกตรวจว่าเป็นลบ คือหาไม่เจอ พลาดสิ่งที่ต้องการตรวจเจอไป
บ่อยครั้งที่ค่าความเที่ยงกับค่าความระลึกได้นั้นสวนทางกัน
ยกตัวอย่างเช่น เราค้นหาเว็บที่ต้องการในกูเกิล ยิ่งผลการค้นหาออกมามากก็มีโอกาสที่ของที่ต้องการจะอยู่ในนั้นมาก แต่ของที่ไม่จำเป็นก็โผล่ออกมาเยอะตาม
นั่นก็คือ ถ้าแค่เข้าข่ายสักหน่อยก็ตัดสินว่าใช่แล้ว ความระลึกได้จะสูง แต่ความเที่ยงจะต่ำ เพราะหาเจอสิ่งที่ต้องการได้มาก แต่ก็มีสิ่งที่ไม่ใช่โผล่มาเพิ่ม
แต่ถ้าต้องรอให้มั่นใจมากๆจึงจะตัดสินใจว่าใช่ ความเที่ยงจะสูง แต่ความระลึกได้จะสูง เพราะสิ่งที่หาได้ส่วนใหญ่ใช่หมด แต่ก็ตกหล่นของที่ควรจะหาได้ไปอีกเยอะ
ค่าไหนจะสำคัญมากหรือน้อยกว่าก็อาจขึ้นกับกรณี เช่นถ้าเป็นการตรวจหาโรคละก็ กรณีนี้การตรวจให้เจอโรคจะสำคัญ ดังนั้นความระลึกได้ควรจะต้องสูง
ถ้ามีใครที่เป็นโรคแต่กลับตัดสินว่าไม่เป็น แบบนั้นอันตราย แต่ถ้าคนที่ไม่เป็นแต่ถูกตัดสินว่าเป็น แบบนั้นอาจไม่เสียหายเท่า ดังนั้นกรณีแบบนี้ถ้าให้ผลเป็นบวกง่ายไว้จะดีกว่า
เมื่อนำความเที่ยงกับความระลึกได้มาเฉลี่ยกันก็จะได้เป็นค่าที่เรียกว่าคะแนน f1
เพียงแต่ว่าไม่ใช่การเฉลี่ยโดยตรง แต่เป็นการเฉลี่ยส่วนกลับ เหมือนเวลาบวกความต่างศักย์ของถ่านที่ต่อกันแบบขนาน แบบนี้เรียกว่าค่าเฉลี่ยฮาร์มอนิก
กล่าวคือ
1/f1 = 0.5×(1/ความเที่ยง + 1/ความระลึกได้)
หรือจะคำนวณได้ว่า
f1 = 2×บวกจริง/(2×บวกจริง+บวกปลอม+ลบปลอม)
= 2×จำนวนที่ทายว่าเป็นบวกและเป็นบวกจริง/(จำนวนที่ทายว่าเป็นบวก+จำนวนที่ผลจริงๆเป็นบวก)
เราอาจสร้างฟังก์ชันคำนวณค่าต่างๆเหล่านี้ในไพธอนได้โดย
maenyam = lambda y,t:(t==y).mean()
thiang = lambda y,t:(1==y[t==1]).mean()
raluek = lambda y,t:(t[y==1]==1).mean()
f1 = lambda y,t:2*(t*y).sum()/(y.sum()+t.sum())นอกจากนี้ใน sklearn ก็ได้มีเตรียมฟังก์ชันพวกนี้ไว้อยู่แล้ว จะนำมาใช้ก็ได้เช่นกัน
from sklearn.metrics import accuracy_score as maenyam
from sklearn.metrics import precision_score as thiang
from sklearn.metrics import recall_score as raluek
from sklearn.metrics import f1_score as f1ลองยกตัวอย่าง เช่น ใช้เครื่องตรวจอาการป่วยวินิจฉัยโรคให้ผู้ป่วย ๑๐ คนโดยในนั้นมีผู้ป่วยจริงๆอยู่ ๓ คน
แต่ว่าอุปกรณ์วัดที่ใช้มีอยู่หลายตัว ให้ผลวินิยฉัยต่างกันไป เมื่อนำมาเปรียบเทียบกับค่าจริง ผลคะแนนที่ได้ออกมาเป็นดังนี้
bok = lambda y,t:u'แม่น=%.3f : เที่ยง=%.3f : ระลึก=%.3f : f1=%.3f'%(maenyam(y,t),thiang(y,t),raluek(y,t),f1(y,t))
y = np.array([0,0,0,0,0,0,0,1,1,1])
print(bok(y,np.array([0,0,0,0,0,0,0,0,0,1])))
print(bok(y,np.array([0,0,0,0,0,1,1,1,1,1])))
print(bok(y,np.array([0,1,1,1,1,1,1,1,1,1])))
print(bok(y,np.array([0,0,0,0,1,1,1,1,1,0])))ผลที่ได้
แม่น=0.800 : เที่ยง=1.000 : ระลึก=0.333 : f1=0.500
แม่น=0.800 : เที่ยง=0.600 : ระลึก=1.000 : f1=0.750
แม่น=0.400 : เที่ยง=0.333 : ระลึก=1.000 : f1=0.500
แม่น=0.600 : เที่ยง=0.400 : ระลึก=0.667 : f1=0.500อันที่ 2 ทายแม่นเท่าอันที่ 1 แต่กลับได้คะแนน f1 เยอะกว่า
ส่วนอันที่ 3 กับ 4 ทายแม่นน้อยกว่าอันที่ 1 เยอะแต่กลับได้ค่า f1 เท่ากัน
ดังนั้นจะเห็นได้ว่าในบางกรณีคะแนนที่พิจารณาจาก f1 จะต่างจากค่าความแม่นยำ ดังนั้นการเลือกว่าจะให้คะแนนด้วยวิธีไหนจึงเห็นผลได้ชัด
คะแนน f1 ยังอาจใช้เพื่อพิจารณาปัญหาการแบ่งกลุ่มเป็นหลายกลุ่มได้ด้วย เพียงแต่ว่ากรณีนี้จะมีความคลุมเครือ เพราะถ้ามีแค่ ๒ เราจะแบ่งให้ผลอันหนึ่งเป็นบวก และอีกอันเป็นลบ
แต่เมื่อมีหลายกลุ่มอาจทำได้โดยการพิจารณาว่าให้ตัวหนึ่งเป็นบวกที่เหลือเป็นลบ แล้วก็คำนวณค่าความเที่ยงกับความระลึกได้ไปทีนึง จากนั้นก็เปลี่ยนให้อีกตัวเป็นบวกแทน แล้วก็คำนวณใหม่ ไล่ไปให้ทุกตัวได้ถูกพิจารณาเป็นบวกทั้งหมด สุดท้ายก็เอาผลที่ได้ของแต่ละรอบมาเฉลี่ยกัน
เพียงแต่ว่าการเฉลี่ยนั้นอาจเฉลี่ยโดยคิดน้ำหนักตามจำนวนผลที่แต่ละกลุ่มมี ก็จะได้คำตอบต่างกันออกไป
กรณีที่เฉลี่ยทุกกลุ่มด้วยน้ำหนักเท่ากันอาจลองเขียนฟังก์ชันได้ดังนี้
def f1(y,t):
k = len(set(y)^set(t))
y_1h = y[:,None]==range(k)
t_1h = t[:,None]==range(k)
return ((2*(t_1h*y_1h).sum(0)/(y_1h.sum(0)+t_1h.sum(0)))).mean()ส่วนฟังก์ชัน f1_score ของ sklearn นั้นโดยทั่วไปแล้วหากเราป้อนค่าที่ไม่ใช่มีแค่ ๒ กลุ่ม (ไม่ได้มีแค่ 0,1) จำเป็นจะต้องระบุด้วยว่าจะเฉลี่ยแบบไหน
หากต้องการเฉลี่ยให้เท่ากันก็ใส่เป็น average='macro' แต่ถ้าต้องการถ่วงน้ำหนักให้ใส่ average='weighted'
ตัวอย่าง
from sklearn.metrics import f1_score as f1
y = np.array([1,1,1,1,2,0,2,1,1,1])
t = np.array([1,1,1,1,0,2,2,1,1,1])
print(f1(y,t,average='macro')) # ได้ 0.5
print(f1(y,t,average='weighted')) # ได้ 0.8weighted จะได้เยอะกว่า macro เพราะค่า 1 ซึ่งทายถูกหมดนั้นมีจำนวนมาก หากเฉลี่ยโดยถ่วงน้ำหนักคะแนนก็ย่อมสูง แต่ถ้าไม่ถ่วงน้ำหนักก็จะโดนคะแนนของเลข 0 และ 2 ซึ่งทายผิดเยอะดึงลง
ต่อมาลองเอามาใช้ในการวิเคราะห์ผลของปัญหาการวิเคราะห์การถดถอยโลจิสติกดู
สมมุติว่าข้อมูลการตรวจโรคจากสารในร่างกายของคน 1000 คนออกมาเป็นดังนี้ โดยแกนนอนคือปริมาณสาร a แกนนอนคือปริมาณสาร b ส่วนสีของจุดบ่งบอกถึงผล โดยสีเขียวคือผลบวก (มีโรค) สีน้ำเงินคือผลลบ (ไม่มีโรค)

ข้อมูลถูกสร้างโดยโค้ดตามนี้
np.random.seed(2)
X,z = datasets.make_blobs(n_samples=1000,n_features=2,centers=2,cluster_std=2.5,center_box=[2,20])
X = np.abs(X)
plt.axes(aspect=1)
plt.xlabel('ปริมาณสาร a',family='Tahoma')
plt.ylabel('ปริมาณสาร b',family='Tahoma')
plt.scatter(X[:,0],X[:,1],c=z,s=30,alpha=0.3,edgecolor='k',cmap='winter')
plt.show()จากนั้นลองหาพารามิเตอร์ค่าน้ำหนักและไบแอสโดยใช้ LogisticRegression ของ sklearn เพื่อหาเส้นแบ่ง
from sklearn.linear_model import LogisticRegression as Lori
lori = Lori()
lori.fit(X,z)
w = lori.coef_[0]
b = lori.intercept_[0]
x_sen = np.array([X[:,0].min(),X[:,0].max()])
y_sen = -(b+x_sen*w[0])/w[1]
plt.axes(aspect=1)
plt.xlabel('ปริมาณสาร a',family='Tahoma')
plt.ylabel('ปริมาณสาร b',family='Tahoma')
plt.scatter(X[:,0],X[:,1],c=z,s=30,alpha=0.3,edgecolor='k',cmap='winter')
plt.plot(x_sen,y_sen,'--r')
plt.show()
ลองเอาผลการแบ่งนี้มาใช้ทำนายผลของข้อมูลชุดนี้
t = (np.dot(w,X.T)+b)>0
# หรือ t = lori.predict(X) ก็ได้
print(bok(z,t))ได้
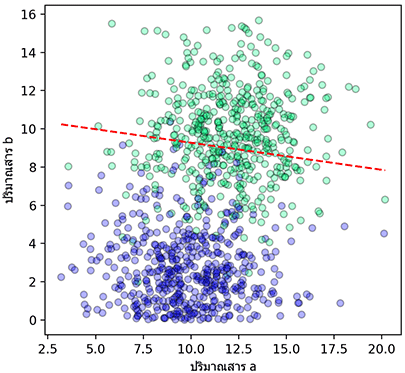
แม่น=0.934 : เที่ยง=0.929 : ระลึก=0.940 : f1=0.934แต่ว่าหากลองปรับไบแอสให้เส้นเลื่อนขึ้นบนไปสักหน่อย โดยที่น้ำหนักเหมือนเดิม
b2 = b-3
t2 = (np.dot(w,X.T)+b2)>0เส้นก็จะเปลี่ยนไปตามนี้

แล้วผลที่ได้ก็จะกลายเป็น
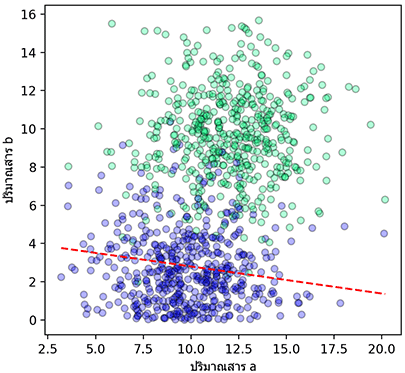
แม่น=0.807 : เที่ยง=0.997 : ระลึก=0.616 : f1=0.761ในทางตรงกันข้ามหากปรับไบแอสให้เส้นเลื่อนขึ้นบน
b3 = b+3
t3 = (np.dot(w,X.T)+b3)>0แม่น=0.788 : เที่ยง=0.703 : ระลึก=0.996 : f1=0.825
นั่นคือความระลึกได้จะเพิ่มขึ้น แต่ความเที่ยงจะลดลง หมายความว่าหาผลบวกที่ต้องการได้เกือบหมด แต่ก็มีที่ไม่ใช่ปนมาด้วยเยอะ
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn