การสร้างแบบจำลองสามมิติเป็นไฟล์ .obj วิธีการอย่างง่ายที่ไม่ว่าใครก็ลองทำได้ทันที
เขียนเมื่อ 2021/10/02 13:20
แก้ไขล่าสุด 2021/10/06 11:33
บทความนี้เขียนขึ้นสำหรับคนที่สนใจเรื่องการสร้างแบบจำลองสามมิติแต่ไม่มีพื้นฐานมาก่อน โดยจะแนะนำวิธีการที่ง่ายที่สุดในการสร้างแบบจำลองสามมิติขึ้นมา โดยไม่ต้องใช้โปรแกรมอะไรเป็นพิเศษ ใช้แค่การเขียนตัวเลขเท่านั้น
รูปแบบของแบบจำลองสามมิตินั้นมีอยู่หลากหลาย แต่โดยพื้นฐานแล้วจะต้องประกอบขึ้นจากจุดยอด (vertex) และหน้าโพลิกอน (polygon) แบบจำลองสามมิตินั้นเป็นรูปเป็นร่างขึ้นมาจากข้อมูลจุดยอดและโพลิกอนเหล่านี้เป็นหลัก
หนึ่งในรูปแบบเก็บข้อมูลแบบจำลองสามมิติที่เป็นที่นิยมเพราะเรียบง่ายและสามารถเปิดอ่านมองตัวเลขแล้วนึกภาพตามได้ก็คือไฟล์
.obj ซึ่งเก็บข้อมูลในรูปแบบตัวหนังสือ สามารถใช้โปรแกรมแก้ไขข้อความเพื่อเปิดอ่านและแก้ค่าตัวเลขได้ และเปิดดูไฟล์ออกมาเป็นตัวแบบจำลองสามมิติได้ด้วยโปรแกรมต่างๆได้หลากหลายปกติคอมพิวเตอร์ในปัจจุบันมักจะมีลงโปรแกรมที่สามารถอ่านไฟล์
.obj ได้อยู่แล้ว โดยไม่ต้องลงเพิ่ม เช่นใน windows 10 จะมีโปรแกรม microsoft 3d viewer เตรียมไว้อยู่แล้วตั้งแต่เริ่ม หากมีไฟล์ .obj ก็สามารถดับเบิลคลิกเปิดดูได้ทันทีดังนั้นในบทความนี้ก็จะขอแสดงแบบจำลองโดยใช้ microsoft 3d viewer นี้เป็นหลัก เพราะไม่ต้องติดตั้งเพิ่มเติม ใครก็สามารถเปิดดูได้ทันที
ส่วนโปรแกรมที่จะใช้สำหรับเขียนแบบจำลองนั้นก็แค่โปรแกรมแก้ไขข้อความอย่างง่าย เช่น notepad ก็เพียงพอแล้ว
เมื่อใช้วิธีนี้ ไม่ว่าใครก็สามารถสร้างแบบจำลองสามมิติขึ้นมาได้เองทันทีอย่างง่ายดาย
การกำหนดตำแหน่งจุดยอดและกำหนดจุดยอดที่ใช้ในแต่ละหน้าโพลิกอน
ก่อนอื่นลองเริ่มจากตัวอย่างที่ง่ายที่สุดก่อนเลย เช่นลองเขียน ๔ บรรทัดนี้ลงในโปรแกรมแก้ไขข้อความ
v 0.2 0.0 0.0
v 0.0 0.5 0.0
v 0.0 0.0 0.8
f 1 2 3แล้วบันทึกลงเป็นไฟล์
.obj เช่นตั้งชื่อว่า samliam.obj เป็นต้นจากนั้นพอเปิดไฟล์
.obj ที่บันทึกไว้ด้วยโปรแกรม microsoft 3d viewer ก็จะได้รูปแบบนี้ขึ้นมา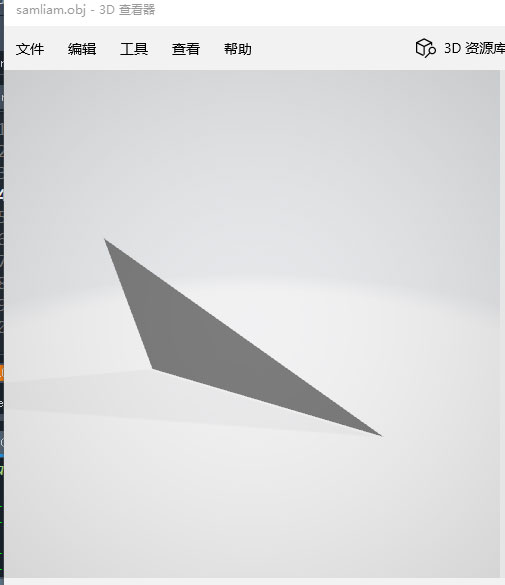
จะเห็นว่าเพียงแค่ข้อมูลตัวเลขแค่ ๑๒ ตัวในข้อความ ๔ บรรทัดนี้ก็สามารถกลายเป็นแบบจำลองสามมิติได้แล้ว นี่เป็นตัวอย่างที่ง่ายที่สุด คือประกอบด้วยจุดยอด ๓ จุด และหน้า ๑ หน้า นั่นคือประกอบด้วยโพลิกอนรูปสามเหลี่ยมอันเดียว
ในที่นี้ตัวเลขที่ตามหลัง v คือตำแหน่งพิกัดในแกน x y z ของจุดยอดแต่ละจุด ตามลำดับ เลขแต่ละตัวจะคั่นด้วยช่องว่าง
ส่วนเลขที่ตามหลัง f คือตัวที่กำหนดว่าในหน้าโพลิกอนหนึ่งๆจะใช้จุดหมายเลขอะไรบ้าง โดยหมายเลขของจุดนั้นจะไล่เรียงตามลำดับ v ที่ใส่ไป โดยเริ่มนับจาก 1
เพียงแค่มีการระบุตำแหน่งจุดยอดแต่ละจุด และหมายเลขของจุดยอดต่างๆที่จะใช้ในแต่ละหน้าโพลิกอน
microsoft 3d viewer นั้นช่วยแสดงรูปร่างของแบบจำลองสามมิติ แต่ไม่ได้แสดงพิกัดหรือสัดส่วนของจุดให้เห็นชัด แต่หากนำไปแสดงในโปรแกรมที่มีการแสดงพิกัดให้เห็นด้วยก็จะเห็นเป็นดังนี้
จะเห็นว่าในที่นี้จุดยอดจุด 1 อยู่ที่ตำแหน่ง (x,y,z)=(0.2,0.0,0.0) จุดที่ 2 อยู่ที่ (0.0,0.5,0.0) จุดที่ 3 อยู่ที่ (0.0,0.0,0.8) ตามตัวเลขที่ระบุไว้นั่นเอง
มีข้อควรระวังอยู่อย่างหนึ่งก็คือ ระบบพิกัดที่ใช้ในงานด้านออกแบบสามมิตินั้นโดยทั่วไปจะใช้ y เป็นแกนตั้ง ต่างจากที่ใช้ในทางคณิตศาสตร์ซึ่งมักใช้ z เป็นแกนตั้ง
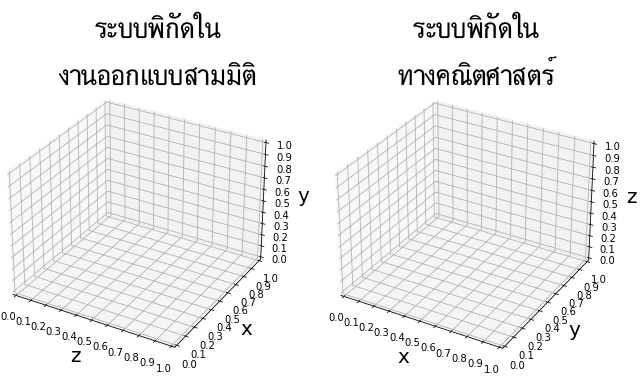
ดังนั้นหากจะเปลี่ยนจากระบบพิกัดทางคณิตศาสตร์เพื่อมาใช้ในการสร้างแบบจำลองสามมิติอาจทำการเปลี่ยนสลับเวียนไปโดย x เป็น z, y เป็น x, z เป็น y
เราสามารถใส่จุดยอดกี่จุดหรือโพลิกอนกี่หน้าก็ได้ตามที่ต้องการ ทั้งหมดนี้ก็จะกลายมาเป็นส่วนประกอบของแบบจำลองสามมิติที่สร้างขึ้นในไฟล์
.obj นี้โดยในหน้าหนึ่งต้องมีอย่างน้อย ๓ จุดยอด อาจมี ๔ จุดขึ้นไปก็ได้ นอกจากนี้แต่ละจุดก็สามารถถูกใช้ในหลายหน้าโพลิกอนได้ในเวลาเดียวกัน
ลองดูอีกตัวอย่าง เช่นลองสร้างให้มีสามเหลี่ยมกับสี่เหลี่ยม ซึ่งมีการใช้จุดร่วมกันอยู่
v 0.1 0.2 0.0
v 0.1 0.2 0.2
v 0.3 0.2 0.2
v 0.3 0.2 0.0
v 0.0 0.0 0.1
f 1 2 3 4
f 1 2 5
เพื่อให้เห็นภาพชัดขึ้น ขอวาดแบบแสดงพิกัดให้เห็นหมายเลขและตำแหน่งชัดเจนอีกทีด้วย
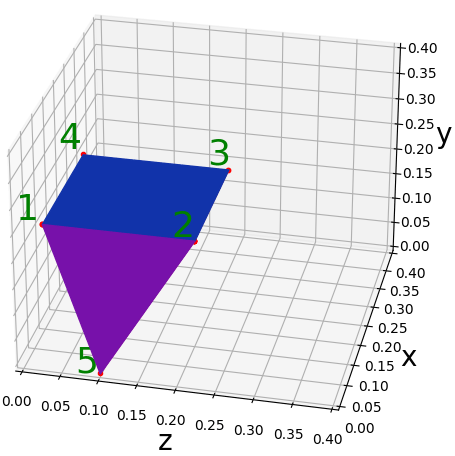
ในที่นี้จุด 1 กับ 2 ถูกใช้ร่วมกันในทั้ง ๒ หน้า ดังนั้นจึงได้โพลิกอนที่ต่อเนื่องกัน
ด้วยวิธีการนี้ เราสามารถสร้างโพลิกอนที่ต่อเนื่องกันไปจนเป็นรูปร่างต่างๆที่ต้องการได้
อีกตัวอย่างเช่นลองทำรูปทรงที่ประกอบขึ้นจากสี่เหลี่ยม ๖ หน้า และจุด ๘ จุด แบบนี้
v -3 0 -3
v 3 0 -3
v 3 0 3
v -3 0 3
v -2 4 -2
v 2 4 -2
v 2 4 2
v -2 4 2
f 1 4 3 2
f 1 2 6 5
f 2 3 7 6
f 3 4 8 7
f 4 1 5 8
f 5 6 7 8
ก็จะได้ทรงรูปร่างคล้ายลูกบาศก์ แค่ในที่นี้วางให้ส่วนฐานแป้นกว่าหน่อยเท่านั้น
จากตัวอย่างที่ยกมานี้คงพอจะทำให้เห็นภาพขึ้นมาได้บ้างแล้วว่าเราจะสามารถสร้างวัตถุสามมิติขึ้นมาได้อย่างไร โดยรวมแล้วโดยพื้นฐานนั้นแบบจำลองก็ประกอบขึ้นมาจากจุดและหน้าดังที่เห็นนี่เอง ดังนั้นต่อให้ไม่มีโปรแกรมอะไร ขอแค่เขียนตัวเลขไปเรื่อยๆก็ได้แบบจำลองสามมิติออกมาแล้ว
แต่ว่ายิ่งรูปทรงซับซ้อนก็ยิ่งมีจำนวนจุดและหน้ามาก ซึ่งก็ยิ่งทำให้ต้องเขียนยาว เต็มไปด้วยตัวเลขของตำแหน่งจุดยอดและหมายเลขของจุดยอดในแต่ละโพลิกอน
เช่นทรงทรงยี่สิบหน้า ซึ่งประกอบขึ้นจาก ๑๒ จุดและ ๒๐ ด้าน ก็เขียนแทนได้ด้วยโค้ดตามนี้
v 0.0 0.0 -1.0
v 0.724 0.526 -0.447
v -0.276 0.851 -0.447
v -0.894 0.0 -0.447
v -0.276 -0.851 -0.447
v 0.724 -0.526 -0.447
v 0.894 0.0 0.447
v 0.276 0.851 0.447
v -0.724 0.526 0.447
v -0.724 -0.526 0.447
v 0.276 -0.851 0.447
v 0.0 0.0 1.0
f 1 3 2
f 1 4 3
f 1 5 4
f 1 6 5
f 1 2 6
f 2 3 8
f 3 4 9
f 4 5 10
f 5 6 11
f 6 2 7
f 2 8 7
f 3 9 8
f 4 10 9
f 5 11 10
f 6 7 11
f 7 8 12
f 8 9 12
f 9 10 12
f 10 11 12
f 11 7 12
แบบนี้ถ้าหากนั่งพิมพ์ตัวเลขเอาเองก็คงจะไม่ใช่เรื่องง่าย แถมอาจเกิดข้อผิดพลาดได้ง่ายด้วย ดังนั้นในทางปฏิบัติแล้ว หากต้องการสร้างรูปทรงซับซ้อนมากๆก็ยังคงต้องใช้โปรแกรมช่วยในการเขียนอยู่ดี
แต่ถ้าเป็นรูปทรงง่ายๆก็ยังอาจใช้วิธีนี้ได้อยู่
การใส่วัสดุพื้นผิวในหน้าโพลิกอน
หลังจากที่ได้แนะนำส่วนประกอบที่สำคัญที่ขาดไม่ได้ของแบบจำลองสามมิติ นั่นคือจุดยอดและหน้าโพลิกอนไปแล้ว คราวนี้จะมาแนะนำส่วนประกอบอื่นๆที่สามารถใส่เพิ่มเติมได้
เริ่มจากเรื่องของ วัสดุ (material) ที่ทาลงบนแต่ละหน้าโพลิกอน ซึ่งเป็นตัวกำหนดลักษณะของพื้นผิวของหน้านั้นๆ เช่นสี ลวดลาย ความโปร่งใส ความเรียบ ความสามารถในการสะท้อนแสง
ไฟล์
.obj นั้นปกติจะเขียนระบุแค่ข้อมูลของจุดยอดและหน้าโพลิกอน แต่ไม่ได้ใส่ข้อมูลวัสดุไว้ด้วย อย่างไรก็ตาม ไฟล์ .obj มักจะใช้คู่กับไฟล์ .mtl ซึ่งใช้เขียนข้อมูลของวัสดุที่จะใช้เอาไว้การเขียนไฟล์
.obj โดยระบุวัสดุที่ใช้นั้นทำได้โดยเขียน mtllib แล้วใส่ชื่อไฟล์ .mtl ที่เขียนข้อมูลวัสดุไว้ จากนั้นใช้เขียน usemtl ตามด้วยชื่อวัสดุ ในบรรทัดก่อนข้อมูลหน้าโพลิกอนที่ต้องการให้ใช้วัสดุนั้นตัวอย่างเช่น ลองสร้างไฟล์
.obj ที่มีหน้าโพลิกอน ๒ หน้าที่ใช้วัสดุต่างกันดังนี้v 0.8 0.0 0.0
v 0.8 0.0 1.3
v 0.3 0.0 1.3
v 0.3 0.5 0.9
mtllib saisi.mtl
usemtl mtl1
f 1 2 3
usemtl mtl2
f 1 2 4จากนั้นในไฟล์
saisi.mtl ก็เขียนข้อมูลของวัสดุไว้ ดังนี้newmtl mtl1
Kd 0.4 0.7 0.3
newmtl mtl2
Kd 0.7 0.3 0.4บันทึกไฟล์
.mtl นี้ไว้ที่เดียวกันกับ .obj แล้วเปิดไฟล์ .obj ออกมาก็จะได้ภาพแบบนี้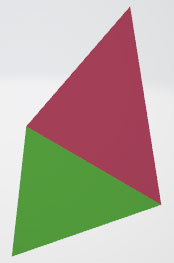
การสร้างข้อมูลวัสดุนั้นก็เรียบง่าย โดยประกอบด้วย newmtl ตามด้วยชื่อวัสดุที่จะสร้าง แล้วในบรรทัดถัดมาก็ตามด้วยข้อมูลต่างๆของวัสดุตัวนั้น โดยพื้นฐานที่สุดแล้วก็คือค่าสีผิวของหน้านั้นๆ ซึ่งระบุโดยใส่ตัวเลขที่แสดงค่าสี (แดง, เขียว, น้ำเงิน) ตามหลัง Kd ดังนั้นในตัวอย่างนี้จึงได้วัสดุสีเขียวกับสีแดงออกมา
นอกจาก Kd แล้วก็ยังมีค่าอื่นๆที่อาจใส่เพิ่มเติมได้อีก เช่น Ks ซึ่งเป็นตัวกำหนดสีสะท้อน ถ้าใส่แล้วจะทำให้วัสดุแวววาวขึ้นมา พอหมุนไปดูด้านต่างๆก็จะเห็นความเปลี่ยนแปลงมาก
เช่นลองใส่วัสดุตามนี้ให้กับทรงยี่สิบหน้าที่สร้างขึ้นมาในตัวอย่างที่แล้ว
newmtl mtl1
Kd 0.2 0.8 0.3
Ks 0.8 0.1 0.4ก็จะได้ทรงยี่สิบหน้าสีเขียวที่มีแสงสะท้อนเป็นสีออกแดงๆแบบนี้ ลองหมุนภาพเพื่อดูมุมต่างๆกันก็จะเห็นสีสะท้อนต่างกันไปในแต่ละมุม

อีกค่าที่สำคัญก็คือ d ซึ่งใช้ระบุความทึบแสงในแต่ละสีของวัสดุ โดยถ้าไม่ได้ใส่ก็จะเป็นค่า 1 1 1 คือทึบแสงโดยสมบูรณ์ แต่ถ้าใส่ค่าที่น้อยกว่า 1 ลงไปก็จะมองทะลุได้ ถ้าเป็น 0 ก็จะใสจนมองทะลุได้หมด
ลองใส่วัสดุที่ระบุค่าความทึบแสงดังนี้ลงบนทรงสิบสองหน้าดู
newmtl mtl1
Kd 0.7 0.2 0.9
d 0.4 0.8 0.1ก็จะได้ออกมาเป็นแบบนี้

นอกจากนี้ยังมีค่าอีกหลายอย่างที่สามารถใส่เป็นตัวปรับแต่งเพิ่มเติมได้อีก แต่ในที่นี้จะขอแนะนำแค่ส่วนหนึ่งที่ใช้บ่อย
การใช้เท็กซ์เจอร์และการกำหนดพิกัดวางภาพบนโพลิกอน
วัสดุนั้นนอกจากจะใช้เป็นแค่สีเดียวซึ่งระบุโดยใช้ Kd ดังในตัวอย่างที่ผ่านมาแล้ว ยังอาจใช้เป็นรูปภาพได้ด้วย ภาพที่ถูกใช้เป็นวัสดุนั้นเรียกว่าเป็น เท็กซ์เจอร์ (texture)
การใช้เท็กซ์เจอร์นั้นจะเพิ่มความยุ่งยากขึ้นมาอีกเล็กน้อย โดยต้องเพิ่มข้อมูลของจุดยอดลงไปอีก จากเดิมที่ใส่แค่ตำแหน่งของจุดยอดในพิกัดสามมิติที่ต้องการวางแล้ว คราวนี้ยังต้องใส่ตำแหน่งของจุดยอดต่างๆภายในภาพที่ใช้เป็นเท็กซ์เจอร์นั้นๆ ค่าพวกนี้มักเรียกว่าเป็นค่า uv
การใส่ค่า uv นั้นทำได้โดยเขียนตัวเลข ๒ ตัวตามหลัง vt จากนั้นเมื่อระบุจุดของแต่ละหน้าในโพลิกอนนั้น หลัง f นอกจากจะใส่ค่าที่ระบุว่าจะใช้ v ตัวไหน ก็ต้องเขียนระบุว่าจะใช้ vt ตัวไหนในหน้านั้นๆด้วย โดยคั่นด้วยทับ "/" ใส่หมายเลขของ v ไว้ทางซ้าย และหมายเลขของ vt ไว้ทางขวา
ตัวอย่างเช่น เราอาจลองใช้ภาพนี้เป็นวัสดุ
ให้ลองบันทึกไฟล์รูปภาพนี้ลงไป ในที่นี้ขอใช้ชื่อว่า
qbicon.png จากนั้นสร้างไฟล์ .obj ขึ้นมาดังนี้v 0.0 0.0 0.0
v 0.0 0.2 0.0
v 0.1 0.0 0.0
v 0.1 0.2 0.0
v 0.1 0.0 0.1
v 0.1 0.2 0.1
vt 0.0 0.0
vt 0.0 1.0
vt 0.5 0.0
vt 0.5 1.0
vt 1.0 0.0
vt 1.0 1.0
mtllib saiphap.mtl
usemtl qb
f 1/1 2/2 4/4 3/3
f 3/3 4/4 6/6 5/5แล้วใน
saiphap.mtl ก็เขียนแบบนี้newmtl qb
map_Kd qbicon.png
Ks 0.5 0.5 0.5ก็จะพบว่าภาพนี้ถูกแปะลงบนหน้าโพลิกอนดังที่ต้องการ

ในที่นี้แทนที่จะใช้ Kd เพื่อแค่ระบุสีเฉยๆ ก็เปลี่ยนเป็น map_Kd เพื่อระบุภาพที่จะใส่
พิกัดของจุดยอดในเท็กซ์เจอร์นั้นจะมีค่าอยู่ในช่วง 0 ถึง 1 โดยที่แนวนอนเรียกเป็นแกน u แนวตั้งเป็นแกน v จึงมักเรียกกันว่า uv
ไม่ว่าภาพจะมีขนาดเท่าไหร่ก็ตาม การระบุพิกัดใน uv นั้นจะหารด้วยขนาดของภาพนั้นให้ uv อยู่ในช่วง 0 ถึง 1 เสมอ
อย่างภาพในตัวอย่างที่ยกมานี้หากวางลงในพิกัด uv ก็จะได้แบบนี้
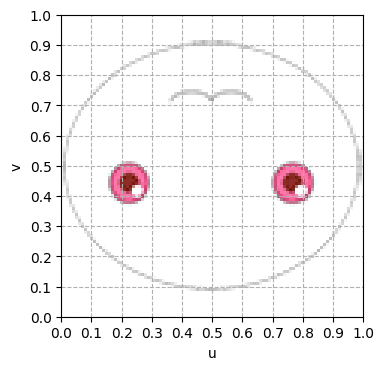
ปกติแล้วในภาพมักจะให้ด้านบนสุดเป็นค่า 0 แต่ค่า v ใน uv มักให้ค่า 0 อยู่ด้านล่าง เมื่อวาดลงบนพิกัด uv ภาพก็เลยกลับหัวอย่างที่เห็น
เวลาระบุตำแหน่งในพิกัด uv จึงต้องระวังตรงนี้ด้วย ไม่เช่นนั้นภาพจะกลับบนล่างแล้วออกมาแปลกๆได้
การกำหนดเวกเตอร์แนวฉาก
นอกจากตำแหน่งพิกัดในระนาบสามมิติและตำแหน่งในระนาบ uv แล้วอีกส่วนประกอบที่สำคัญของหน้าโพลิกอนก็คือสิ่งที่เรียกว่า เวกเตอร์แนวฉาก ซื่งในภาษาอังกฤษใช้คำว่า normal ซึ่งโดยทั่วไปมีความหมายว่า "ปกติ" ดังนั้นในภาษาไทยเลยมีบางคนแปลเป็น "เส้นปกติ" ด้วย แต่จริงๆแล้ว normal ในที่นี้ไม่ได้หมายถึงปกติ แต่หมายถึง "ตั้งฉาก"
เวกเตอร์แนวฉากนั้นเป็นลูกศรที่ชี้ออกจากผิวโพลิกอน เป็นตัวบอกว่าตรงนั้นมีทิศหันไปทางไหน โดยใช้เวกเตอร์เพื่อแสดงทิศ
แบบจำลองสามมิติอาจจะไม่ได้จำเป็นต้องระบุเวกเตอร์แนวฉากเสมอไป ซึ่งหากไม่ได้ระบุไว้ เวกเตอร์แนวฉากก็มักจะถูกกำหนดขึ้นเองซึ่งอาจแล้วแต่การทำงานของแต่ละโปรแกรมที่เปิดใช้
ซึ่งโดยทั่วไปแล้วเราก็อาจไม่ต้องใส่ใจมากกว่าเวกเตอร์แนวฉากของแต่ละจุดยอดนั้นหันไปทางไหน แต่ว่าเวลาที่แสดงแบบจำลองโดยมีแสงส่องนั้นจะเห็นความแตกต่างชัด เพราะความสว่างหรือการสะท้อนแสงของหน้าโพลิกอนจะขึ้นอยู่กับทิศทางการหันของแต่ละจุดในหน้านั้น แม้จะอยู่จุดเดียวกันอยู่แต่ถ้าเวกเตอร์แนวฉากหันไปคนละทิศกันก็จะเห็นมีความสว่างต่างกันได้
ตัวอย่างเช่นลองสร้างโพลิกอน ๒ หน้าที่ใช้จุดยอด ๔ จุด โดยมีการใช้จุด 1 กับ 3 ร่วมกัน แบบนี้
v 0 0 0
v 0.5 0 0
v 0.5 0.5 0
v 0 0.5 0
f 1 2 3
f 3 4 1จะเห็นว่าโพลิกอนสามเหลี่ยมทั้ง ๒ หน้านี้ดูแล้วติดเหมือนเป็นเนื้อเดียว เพราะหันไปทางเดียวกัน รับแสงทางเดียวกัน

แต่หากกำหนดเวกเตอร์แนวฉากของทั้ง ๒ หน้าให้ต่างกันไป ก็จะเห็นผลความแตกต่างขึ้นมาได้
การกำหนดเวกเตอร์แนวฉากทำได้โดยเขียนค่าเวกเตอร์นั้นตามหลัง vn จากนั้นตอนเขียน f ก็ใส่หมายเลขแสดงลำดับของ vn ที่จะใช้ไว้ต่อจาก v และ vt โดยใช้ทับ "/" คั่น เพียงแต่ในกรณีที่ต้องการระบุ vn โดยไม่ระบุ vt ก็ให้ใส่เป็น "//" โดยเว้นส่วน vt ไว้
เช่นลองเขียนตัวอย่างที่แล้วใหม่โดยเพิ่มเวกเตอร์แนวฉากลงไปให้แต่ละหน้าหันไปคนละทางกันจะเขียนได้แบบนี้
v 0 0 0
v 0.5 0 0
v 0.5 0.5 0
v 0 0.5 0
vn 0.0 0.0 1.0
vn 0.0 0.0 -1.0
f 1//1 2//1 3//1
f 3//2 4//2 1//2
จะเห็นว่าแม้จะใช้จุดเดียวกันแต่เพราะถูกเวกเตอร์แนวฉากดึงให้หันไปในทิศทางต่างกัน แสงที่ส่องมาจะทำให้เห็นความแตกต่างว่าไม่ใช่หน้าเดียวกัน
เวกเตอร์แนวฉากนั้นอาจเป็นอะไรที่มองเห็นภาพยาก เพื่อให้เข้าใจได้ง่าย ในที่นี้จะวาดเส้นเวกเตอร์ให้ดู จะได้ดังนี้
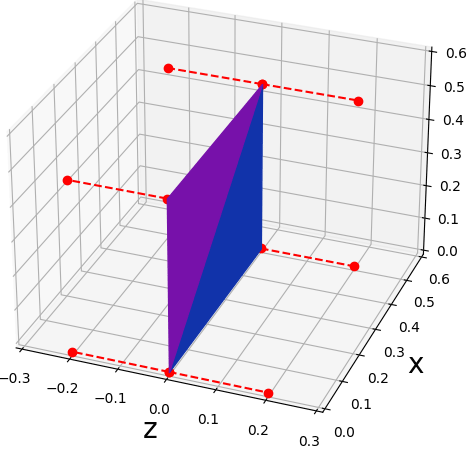
ในที่นี้มุมทั้ง ๓ มุมของหน้าหนึ่งถูกดึงไปทางทิศ z อีกหน้าถูกดึงไปทาง -z ตามเวกเตอร์
โดยทั่วไปเวกเตอร์แนวฉากจะเขียนในรูปของเวกเตอร์หน่วย (คือมีค่า x2+y2+z2=1) แต่เวลาเขียนในไฟล์
.obj ถึงจะไม่ทำเป็นเวกเตอร์หน่วยก็จะถูกหารให้เป็นเวกเตอร์หน่วยโดยอัตโนมัติเวกเตอร์แนวฉากของแต่ละจุดในหน้าอาจไม่จำเป็นต้องไปทางเดียวกันก็ได้ ขึ้นอยู่กับว่าเราต้องการให้หน้านั้นดูเป็นระนาบเรียบหรือว่าดูมีความโค้ง
เพื่อให้เห็นภาพ ลองดูอีกตัวอย่าง โดยลองสร้างพีระมิด ๔ หน้าขึ้นมา กำหนดให้เวกเตอร์แนวฉากของจุดในโพลิกอนหน้าเดียวกันหันไปทางเดียวกัน แต่ละหน้าหันไปคนละทาง
v 0.0 0.0 -1.0
v -1.0 0.0 -0.0
v -0.0 0.0 1.0
v 1.0 0.0 0.0
v 0.0 0.500000 0.0
vn -0.408248 0.816497 -0.408248
vn -0.408248 0.816497 0.408248
vn 0.408248 0.816497 0.408248
vn 0.408248 0.816497 -0.408248
f 1//1 2//1 5//1
f 2//2 3//2 5//2
f 3//3 4//3 5//3
f 4//4 1//4 5//4ผลที่ได้ก็จะได้พีระมิดที่ดูมีขอบเป็นเหลี่ยมชัดเจนแบบนี้ รอยแบ่งของแต่ละหน้าดูชัดเจน

ถ้าวาดภาพแสดงเส้นเวกเตอร์แนวฉากด้วยก็จะเป็นดังนี้
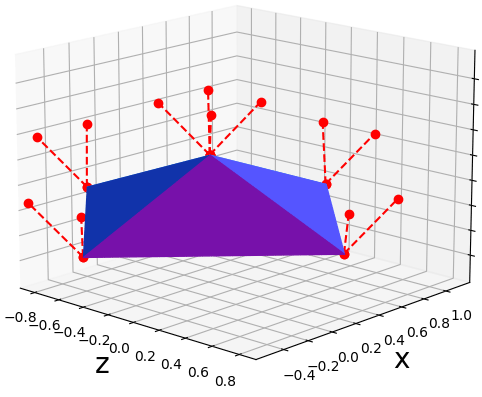
แต่หากลองเปลี่ยนเป็นกำหนดให้เวกเตอร์แนวฉากของจุดยอดเดียวกันหันไปทางเดียวกัน เช่น
v 0.0 0.0 -1.0
v -1.0 0.0 -0.0
v -0.0 0.0 1.0
v 1.0 0.0 0.0
v 0.0 0.500000 0.0
vn 0.0 0.894 -0.447
vn -0.447 0.894 -0.0
vn -0.0 1.0 -0.0
vn -0.0 0.894 0.447
vn 0.447 0.894 0.0
f 1//1 2//2 5//3
f 2//2 3//4 5//3
f 3//4 4//5 5//3
f 4//5 1//1 5//3ก็จะได้ขอบที่ดูเหมือนโค้งมนขึ้นมา เพราะตรงนั้นกำหนดให้ทิศของแต่ละหน้าที่ขอบหันไปทางเดียวกันอยู่

ถ้าวาดเส้นเวกเตอร์แนวฉากก็จะได้ดังนี้
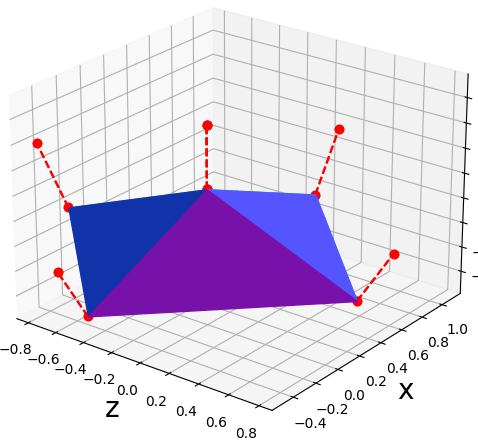
ปกติแล้วโพลิกอนจะเป็นรูปหลายเหลี่ยม ไม่สามารถทำเป็นเส้นโค้งได้ แต่เราสามารถจำลองเส้นโค้งขึ้นมาได้โดยใช้เวกเตอร์แนวฉากดังที่เห็นนี้เอง
ตัวอย่างทิ้งท้าย
สุดท้ายนี้ จากความเข้าใจเรื่องโค้ดในไฟล์
.obj ที่ได้จากการอธิบายข้างต้น เราจะลองเอามาใช้สร้างลูกเต๋ากันดูเท็กซ์เจอร์ของแต่ละหน้าลูกเต๋านั้นก็ได้เตรียมไว้ให้ในไฟล์ดังนี้
naluktao.png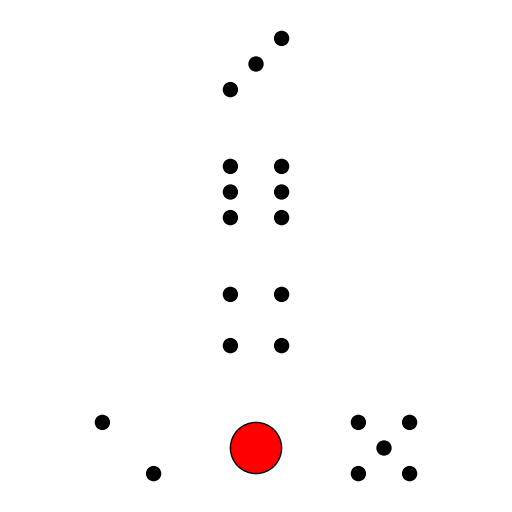
ในไฟล์
luktao.objmtllib naluktao.mtl
v -1.0 0.0 1.0
v 1.0 0.0 1.0
v -1.0 2.0 1.0
v 1.0 2.0 1.0
v -1.0 2.0 -1.0
v 1.0 2.0 -1.0
v -1.0 0.0 -1.0
v 1.0 0.0 -1.0
vt 0.375 0.0
vt 0.625 0.0
vt 0.375 0.25
vt 0.625 0.25
vt 0.375 0.5
vt 0.625 0.5
vt 0.375 0.75
vt 0.625 0.75
vt 0.375 1.0
vt 0.625 1.0
vt 0.875 0.0
vt 0.875 0.25
vt 0.125 0.0
vt 0.125 0.25
vn 0.0 0.0 1.0
vn 0.0 1.0 0.0
vn 0.0 0.0 -1.0
vn 0.0 -1.0 0.0
vn 1.0 0.0 0.0
vn -1.0 0.0 0.0
usemtl naluktao
f 1/1/1 2/2/1 4/4/1 3/3/1
f 3/3/2 4/4/2 6/6/2 5/5/2
f 5/5/3 6/6/3 8/8/3 7/7/3
f 7/7/4 8/8/4 2/10/4 1/9/4
f 2/2/5 8/11/5 6/12/5 4/4/5
f 7/13/6 1/1/6 3/3/6 5/14/6ในไฟล์
naluktao.mtl โดยลายหน้าลูกเต๋ากำหนดโดยไฟล์เท็กซ์เจอร์ แล้วตั้ง Ks ให้มีการสะท้อนแสง ตั้ง d ให้มีความโปร่งใสเล็กน้อยnewmtl naluktao
map_Kd naluktao.png
d 0.8 0.8 0.8
Ks 0.5 0.5 0.5ผลที่ได้ก็จะออกมาเป็นลูกเต๋าใสๆแวววาวอย่างที่เห็นนี้

สรุปทิ้งท้าย
ที่แนะนำไปข้างต้นนั้นเป็นแค่คุณสมบัติพื้นฐานของแบบจำลองสามมิติที่มักจะใช้กันมาก แต่จริงๆแล้วยังมีรายละเอียดต่างๆอีกมากมาย ซึ่งไม่ได้เขียนถึงในที่นี้ เนื่องจากจะต้องลงลึกมาก และมักมีความแตกต่างกันไปขึ้นอยู่กับโปรแกรมที่ใช้
กล่าวโดยสรุปแล้ว แบบจำลองสามมิติจะประกอบไปด้วยส่วนประกอบต่างๆ เรียงลำดับตามความสำคัญได้ดังนี้
- จุดยอด (vertex)
- หน้าโพลิกอน (polygon)
- วัสดุ (material)
- เท็กซ์เจอร์ (texture)
- เวกเตอร์แนวฉาก (normal)
ถ้าเข้าใจพื้นฐานของส่วนประกอบต่างๆเหล่านี้ อย่างน้อยก็น่าจะสามารถทำการออกแบบสามมิติอย่างง่ายได้แล้ว
สรุปค่าต่างๆที่เขียนภายในไฟล์
.obj ได้ดังนี้| คีย์เวิร์ด | ความหมาย | ค่า |
|---|---|---|
| v | ตำแหน่งจุดยอดในพิกัด xyz | จำนวนจริง ๓ ตัว |
| vt | ตำแหน่งจุดยอดในพิกัด uv ของเท็กซ์เจอร์ | จำนวนจริง ๒ ตัว |
| vn | เวกเตอร์แนวฉาก | จำนวนจริง ๓ ตัว |
| f | หมายเลขของแต่ละหน้าที่ใช้ในโพลิกอน | จำนวนเต็ม ๓ ตัวขึ้นไป |
| mtllib | ชื่อไฟล์ .mtl ที่เขียนข้อมูลวัสดุ | ตัวหนังสือ |
| usemtl | ชื่อวัสดุที่จะใช้กับหน้าโพลิกอน | ตัวหนังสือ |
ค่าต่างๆในไฟล์
.mtl| คีย์เวิร์ด | ความหมาย | ค่า |
|---|---|---|
| newmtl | ชื่อวัสดุใหม่ที่จะสร้าง | ตัวหนังสือ |
| Kd | สีพื้นฐาน | จำนวนจริงค่า [0,1] ๓ ตัว |
| Ks | สีสะท้อน | จำนวนจริงค่า [0,1] ๓ ตัว |
| d | ความทึบแสงของสีต่างๆ | จำนวนจริงค่า [0,1] ๓ ตัว |
| Map_Kd | ชื่อไฟล์ที่จะใช้เป็นเท็กซ์เจอร์ | ตัวหนังสือ |