ทำความเข้าใจการแปลงลาปลัสสำหรับแก้ปัญหาฟิสิกส์

เขียนเมื่อ 2025/10/04 18:54

แก้ไขล่าสุด 2025/10/05 13:24

บทความนี้จะอธิบายเกี่ยวกับการแปลงลาปลัส (Laplace transform) โดยเน้นไปที่การทำความเข้าใจเพื่อนำมาใช้ในทางด้านฟิสิกส์หรือวิศวกรรม ไม่ลงลึกทางคณิตศาสตร์ แต่ให้ความสำคัญตรงที่ว่าจะนำมาใช้อย่างไร

เนื้อหาเน้นไปที่คนเรียนด้านฟิสิกส์หรือวิศวกรรม โดยจะถือว่าผู้อ่านมีความรู้ฟิสิกส์และคณิตศาสตร์ระดับมัธยมปลายอยู่แล้ว มีความเข้าใจแคลคูลัส เอกซ์โพเนนเชียล ตรีโกณมิติ และการแก้สมการพหุนาม

ปัญหาการเคลื่อนที่ของวัตถุอย่างง่ายที่ต้องการแก้

ก่อนที่จะมาเรียนรู้วิธีการแปลงลาปลัส ขอเริ่มจากตั้งปัญหาก่อน เพื่อให้นึกภาพได้ว่าเราจะเรียนรู้มันไปทำไม

ปัญหาที่นำการแปลงลาปลัสมาประยุกต์ใช้ได้นั้นมีหลากหลาย แต่ที่ดูจะเห็นภาพง่ายสุดก็คือการเคลื่อนที่ของวัตถุ ซึ่งพบได้ในบทเรียนฟิสิกส์ตั้งแต่ระดับชั้นมัธยมปลาย

$\begin{align} m\ddot{x}(t) = f(t) \end{align}$

โดยในที่นี้ $f(t)$ คือแรงที่กระทำต่อวัตถุ ส่วน $x(t)$ เป็นตำแหน่งของวัตถุ ทั้งคู่เป็นฟังก์ชันของเวลา $t$

โดยจุดในที่นี้แสดงถึงอนุพันธ์เทียบเวลา นั่นคือ $\begin{align} \dot{x}(t) = \frac{d}{dt}x(t) \end{align}$ และ $\begin{align} \ddot{x}(t) = \frac{d^2}{dt^2}x(t) \end{align}$ เป็นฟังก์ชันของเวลา

และ $m$ คือมวลของวัตถุ

ตัวอย่างที่พบได้บ่อยและอธิบายได้ง่ายก็คือระบบรถติดสปริง ซึ่งแรงที่กระทำต่อวัตถุจะแปรตามระยะยืดของสปริง

$\begin{align} f_{สปริง}(t) = - kx(t) \end{align}$

โดย $k$ คือค่าคงตัวสปริง และ $x(t)$ ในที่นี้เป็นตำแหน่งนับจากจุดสมดุลของสปริง

แล้วก็จะได้สมการการเคลื่อนที่เป็นแบบนี้

$\begin{align} m\ddot{x}(t) = - kx(t) \end{align}$

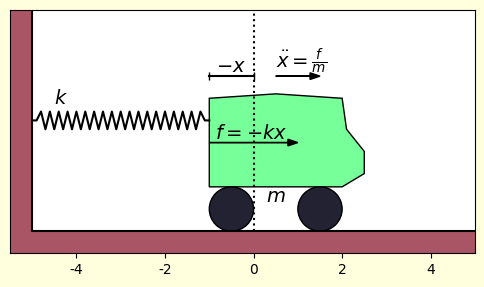
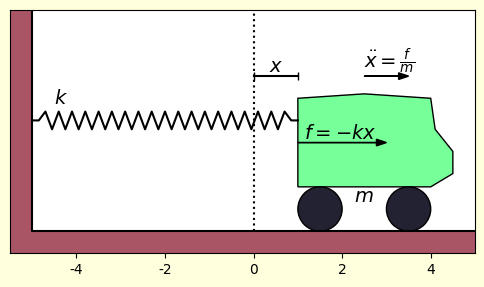
ถ้าระบบง่ายๆแบบนี้ก็จะเกิดการเคลื่อนที่สั่นไปมาเป็นคาบ คือเป็นการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย (simple harmonic) ที่คุ้นเคยกันในบทเรียนชั้นมัธยมปลายนั่นเอง

แต่ในที่นี้เพื่อให้ซับซ้อนขึ้นจะได้เห็นภาพอะไรมากขึ้นจึงขอพิจารณาระบบที่มีตัวหน่วงด้วย

ตัวหน่วงนั้นอาศัยแรงต้านจากความหนืด ซึ่งแปรตามความเร็ว

$\begin{align} f_{ตัวหน่วง}(t) = - c\dot{x}(t) \end{align}$

โดย $c$ คือสัมประสิทธิ์ความหนืด

เมื่อรวมทั้งแรงสปริงและแรงจากตัวหน่วงก็จะได้ว่า

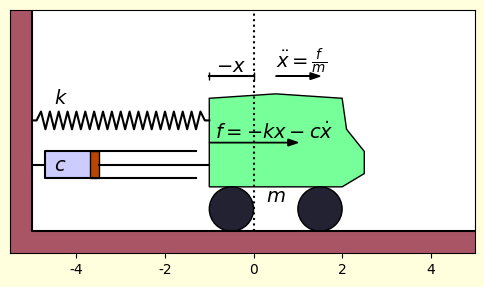
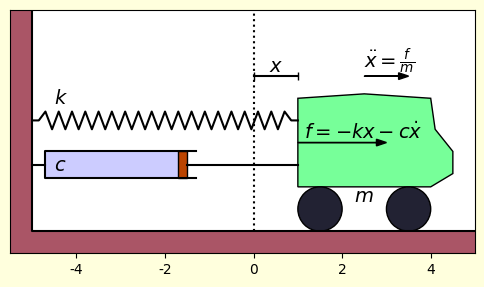
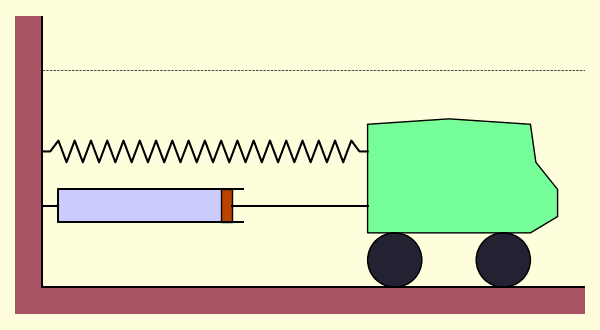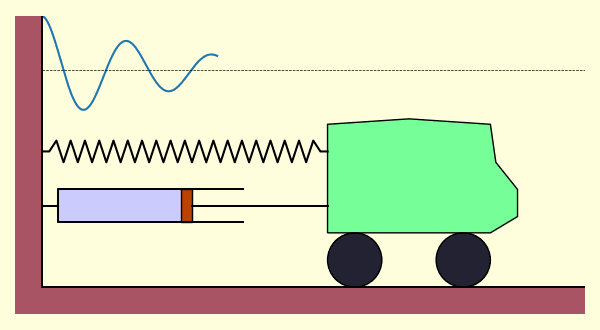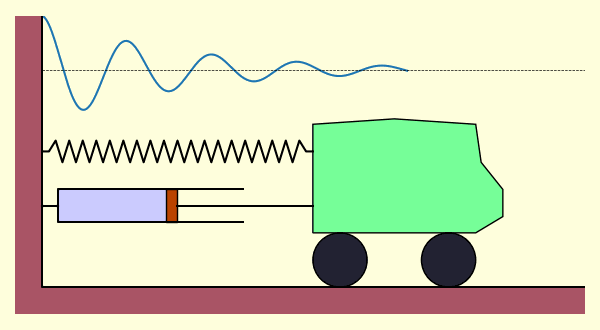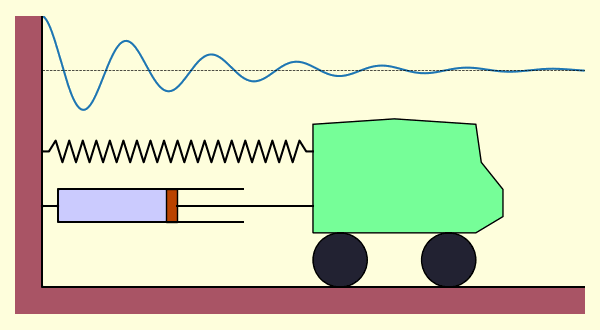
$\begin{align} f(t) = m\ddot{x}(t) = - kx(t) - c\dot{x}(t) \end{align}$

ถ้าลองสร้างเป็นภาพเคลื่อนไหวก็จะได้การเคลื่อนไหวเป็นแบบนี้ คือเคลื่อนไปข้างหน้าและถอยหลังซ้ำไปมา แต่จะมีระยะเคลื่อนสั้นลงเรื่อยๆเนื่องจากโดนหน่วง จนในที่สุดก็จะหยุดนิ่ง

จากสมการข้างบนจัดรูปใหม่ย้ายข้าง

$\begin{align} m\ddot{x}(t) + c\dot{x}(t) + kx(t) = 0 \end{align}$

ได้เป็นลักษณะที่เรียกว่าสมการเชิงอนุพันธ์ (differential equation) หรือเรียกให้เจาะจงกว่านั้นก็คือลักษณะแบบนี้เรียกว่าเป็นสมการเชิงอนุพันธ์สามัญเชิงเส้น (linear ordinary differential equation) แต่รายละเอียดตรงนี้ขอละไว้ไม่ลงลึก เอาเป็นว่าแค่อยากบอกว่าเราต้องการแก้ปัญหาสมการในรูปแบบนี้

สมการเชิงอนุพันธ์แบบนี้นั้นดูเผินๆก็เหมือนจะคล้ายสมการพหุนาม แต่ที่จริงแก้ยากกว่ามาก ถ้าเป็นสมการพหุนามละก็ แยกตัวประกอบแล้วก็แก้ได้ แต่ว่าสมการเชิงอนุพันธ์ไม่ง่ายแบบนั้น เห็นเขียนสั้นๆแค่นี้แต่ผลเฉลยนั้นออกมาซับซ้อนมากทีเดียว

แต่ก็มีวิธีการที่ช่วยให้เราสามารถแก้สมการเชิงอนุพันธ์ได้ง่ายเหมือนกับแก้สมการพหุนาม นั่นก็คือการแปลงลาปลัสนั่นเอง

ฉะนั้นต่อจากนี้ไปจะเริ่มแนะนำการแปลงลาปลัส โดยมีเป้าหมายเบื้องต้นคือการแก้สมการนี้

ภาพรวมของการแปลงลาปลัส

การแปลงลาปลัสถือเป็นการแปลงทางคณิตศาสตร์ชนิดหนึ่งที่มีความสำคัญและมีการนำมาใช้อย่างกว้างขวาง ชื่อนี้ได้รับการตั้งชื่อตามลาปลัสซึ่งเป็นผู้คิดค้น

ซึ่งไม่ใช่ลาปลัสที่เป็นโปเกมอน

แล้วก็ไม่ใช่ลาปลัสจากเรื่องเกิดใหม่เป็นสไลม์ด้วย

แต่เป็นลาปลัสเดียวกับ "ปีศาจของลาปลัส" ที่พูดถึงในเรื่องอาโอบุตะ

ลาปลัสในที่นี้คือ ปีแยร์-ซีมง ลาปลัส (Pierre-Simon Laplace, ปี 1749-1827) เป็นนักคณิตศาสตร์ชาวฝรั่งเศส ผู้มีชื่อเสียงจากการคิดค้นอะไรต่างๆมากมายในทางคณิตศาสตร์ รวมไปถึงฟิสิกส์ ดาราศาสตร์ วิศวกรรม และยังเสนอแนวคิดด้านปรัชญาอย่างเรื่องปีศาจของลาปลัสด้วย

การแปลงลาปลัสก็เป็นหนึ่งในผลงานที่สำคัญที่เป็นที่รู้จักมากที่สุดของเขา โดยไม่ได้มีระบุเวลาที่คิดค้นที่แน่ชัดแต่เชื่อว่าเขาคิดมันขึ้นในช่วงปี 1780 กว่า

การแปลงลาปลัสนั้นมีลักษณะคล้ายคลึงกับการแปลงฟูรีเย (Fourier transform) เป็นอย่างมาก โดยบางครั้งก็ได้รับการมองว่าเป็นการแปลงฟูรีเยที่ถูกนำมาปรับให้ใช้ได้กว้างขวางมากขึ้น อย่างไรก็ตามการแปลงฟูรีเยนั้นถูกคิดขึ้นในช่วงต้นในช่วงต้นศตวรรษที่ 19 จึงมาทีหลัง

แปลงฟูรีเยนั้นถูกใช้อย่างกว้างขวางโดยเฉพาะในการวิเคราะห์คลื่นหรืออะไรก็ตามที่มีการสั่น โดยเห็นภาพชัดเข้าใจง่าย ตีความผลการแปลงได้ตรงตัว ในขณะที่การแปลงลาปลัสนั้นมักถูกมองว่าเข้าใจยากกว่า ไม่ได้มองเห็นความหมายได้ชัดเจนเหมือนอย่างการแปลงฟูรีเย

ถึงอย่างนั้นการแปลงลาปลัสเองก็ได้รับการนำมาประยุกต์ใช้อย่างกว้างขวางในหลายสาขาวิชา แม้จะไม่กว้างเท่าการแปลงฟูรีเยก็ตาม

ตัวอย่างสาขาที่จำเป็นต้องใช้การแปลงลาปลัสเป็นส่วนสำคัญได้แก่สาขาวิศวกรรมระบบควบคุม เพราะระบบควบคุมที่ผ่านการแปลงลาปลัสจะสามารถคำนวณและวิเคราะห์ได้ง่าย

นอกจากนี้ก็ยังมีการนำมาใช้ในด้านการวิเคราะห์วงจรอิเล็กทรอนิก การประมวลผลสัญญาณ และสาขาอื่นอีกมากมายในด้านฟิสิกส์

ตัวอย่างการเคลื่อนที่ของวัตถุที่ยกมาเป็นโจทย์หลักครั้งนี้เองก็เป็นส่วนหนึ่งของเนื้อหาเบื้องต้นของวิศวกรรมระบบควบคุม

แม้ว่าการแปลงลาปลัสจะเป็นอะไรที่ดูเป็นนามธรรมและเข้าใจโดยนึกภาพตามได้ยาก แต่ก็มีประโยชน์จริงในการนำมาใช้คำนวณเพื่อแก้ปัญหาในสาขาต่างๆ ถ้าหากใครที่เรียนหรือทำงานในสาขาที่เกี่ยวข้องก็จำเป็นที่จะต้องทำความเข้าใจ

แน่นอนว่าคนทั่วไปที่ไม่ได้อยู่ในสายถ้าแค่สนใจอยากศึกษาก็ได้ แต่ว่าถ้าไม่เห็นตัวอย่างการใช้งานจริงก็จะยิ่งนึกภาพได้ยาก แต่ถ้ามีเป้าหมายชัดเจนก็น่าจะเข้าใจได้ดีกว่า

นิยามเบื้องต้น

การแปลงลาปลัสมีนิยามดังนี้

$\begin{align} \mathcal{L}[x(t)] = \int_{0}^{\infty}x(t)e^{-st}dt \end{align}$

นั่นก็คือเป็นปริพันธ์ของค่า $x$ ที่เราต้องการพิจารณา ซึ่งเป็นฟังก์ชันของเวลา $t$ คูณกับ $e^{-st}$ ตั้งแต่ $t=0$ ไปจนถึง $t=\infty$

$t$ นั้นในปัญหาทางฟิสิกส์มักจะหมายถึงเวลา แม้ว่าในทางคณิตศาสตร์ทั่วไปแล้วอาจไม่จำเป็นต้องเป็นเวลาเสมอไปก็ได้

ตัว $\mathcal{L}$ นี้คือตัว L ที่เอามาเขียนให้แปลกไปเพื่อแยกจาก L ที่เป็นตัวแปรธรรมดา และสิ่งที่อยู่ในวงเล็บเหลี่ยมข้างหลัง $\mathcal{L}$ คือฟังก์ชันที่ต้องการนำมาแปลง

อนึ่ง ถ้าดูในตำราคณิตศาสตร์ทั่วไปมักนิยมตัวแปรฟังก์ชันเป็นอักษร f มากกว่า แต่ในที่นี้เราเริ่มเกริ่นปัญหาจากเรื่องของตำแหน่งซึ่งใช้ตัวแปรเป็น x ดังนั้นในบทความนี้ก็จะขออธิบายด้วยตัวแปร x ไปทั้งหมดเลยจะได้ไม่สับสน

ในที่นี้จะเห็นว่าข้างในสูตรมีตัวแปรใหม่ $s$ อยู่ที่ $e^{-st}$ ในขณะที่หลังหาปริพันธ์ออกมาแล้วตัวแปรเวลา $t$ ก็หายไป กลายเป็นว่าตัวแปรที่เหลืออยู่จะมีแค่ $s$ นั่นหมายความว่าผลที่ได้จากการแปลงลาปลัสจะเป็นฟังก์ชันของตัวแปร $s$ จึงมักเขียนดังนี้

$\begin{align} X(s) = \mathcal{L}[x(t)] \end{align}$

ตัวแปร $s$ นี้เรียกว่าเป็น ตัวแปรลาปลัส (Laplace variable) และเรียกฟังก์ชัน $X(s)$ นี้ว่าเป็น ผลการแปลงลาปลัสของ $x(t)$

โดยส่วนใหญ่แล้วฟังก์ชันที่ได้จากการแปลงลาปลัสนั้นมักจะเขียนด้วยอักษรตัวพิมพ์ใหญ่ในขณะที่ฟังก์ชันเดิมก่อนแปลงใช้ตัวพิมพ์เล็ก เพื่อให้เห็นว่ามีความสัมพันธ์กัน เช่นครั้งนี้เป็น $x$ กับ $X$ เพียงแต่ว่าก็ไม่ใช่กฎตายตัว เพราะตัวแปรจะใช้ยังไงก็ได้อยู่แล้ว แต่เพื่อให้เข้าใจง่ายก็จะขอใช้ตามนี้

ขอยกตัวอย่างการแปลงอย่างง่ายๆ เช่นลองทำการแปลงลาปลัสสำหรับฟังก์ชันนี้ดู

$\begin{align} x(t) = e^{2t} \end{align}$

ลองคำนวณตามนิยามที่กล่าวมา ได้ดังนี้

$\begin{align} X(s) &= \mathcal{L}\left[e^{2t}\right] \\ &= \int_{0}^{\infty}e^{2t}e^{-st}dt \\ &= \int_{0}^{\infty}e^{(2-s)t}dt \\ &= \frac{1}{s-2} \\ \end{align}$

ดังนั้นก็จะได้ว่าผลการแปลงลาปลัสของ $e^{2t}$ คือ $\frac{1}{s-2}$

ว่าด้วยเรื่องตัวแปรปริศนา s

เมื่อเห็นสูตรการแปลงและตัวอย่างการแปลงแล้วสิ่งต่อไปที่คนน่าจะสงสัยและงงมากที่สุดก็คือตัวแปร $s$ ที่อยู่ๆก็ปรากฏขึ้นมาแทน $t$

แล้ว $s$ นี้คืออะไร? ในเมื่อเรากำลังพิจารณาปัญหาค่าซึ่งเป็นฟังก์ชันของเวลา $t$ อยู่แท้ๆ ทำไมแปลงแล้วกลายเป็นตัวแปรที่ไม่รู้จักโผล่มาแทน

ตรงนี้ต้องบอกว่าเป็นอะไรที่เป็นนามธรรมตีความยากพอสมควรทีเดียว การจะทำความเข้าใจความหมายของการแปลงลาปลัสอย่างแท้จริงไม่ใช่เรื่องง่ายๆ ต้องอาศัยจินตนาการ

และที่จริงคือถ้าจะให้ตอบแบบกำปั้นทุบดินไปเลยก็คือ เป้าหมายสำคัญของการศึกษาการแปลงลาปลัสไม่ใช่การเข้าใจความหมายของมัน แต่เป็นการเข้าใจว่าใช้งานยังไง

เพราะสำหรับนักฟิสิกส์หรือวิศวะแล้ว คณิตศาสตร์ถือเป็นเครื่องมือเพื่อนำมาใช้อธิบายปรากฏการณ์ที่พิจารณา บางทีเราก็ใช้โดยไม่ได้เข้าใจที่มาของมันอย่างลึกซึ้ง ซึ่งที่จริงแล้วถ้าเข้าใจได้มันก็ดีกว่าอยู่แล้ว แต่เนื่องจากว่ามีเทคนิคทางคณิตศาสตร์มากมายที่ถูกนำมาใช้ เป็นการยากที่เราจะมีเวลามาทำความเข้าใจทั้งหมด

แต่ถึงจะพูดอย่างนั้นก็ตาม ถ้าไม่อธิบายเลยก็จะมองไม่เห็นภาพและอาจไปต่อไม่ถูก ดังนั้นในที่นี้ก็จะขออธิบายแบบคร่าวๆในเชิงฟิสิกส์

การแปลงลาปลัสนั้นเป็นการเปลี่ยนมุมมองปัญหา จากที่เดิมเราพิจารณาค่า $x$ ในโลกของเวลา $t$ มาเป็นการพิจารณาค่า $X$ ในโลกของตัวแปรลาปลัส $s$

$\mathcal{L}$

โลกของเวลา $t$

โลกของตัวแปรลาปลัส $s$

$x(t)$

$X(s)$

$e^{2t}$

$\begin{align}\frac{1}{s-2}\end{align}$

เมื่อ $x$ เป็นตำแหน่ง $X$ ก็เป็นอะไรบอกถึงตำแหน่งเหมือนกัน แต่ว่าไม่ใช่ค่าตำแหน่งในลักษณะที่ตึความแบบตรงๆได้

ในลักษณะเดียวกัน $t$ เป็นเวลา และ $s$ ก็เป็นสิ่งที่สัมพันธ์กับเวลาเหมือนกัน แต่ก็ไม่ใช่เวลา และถ้าพิจารณาดูมิติแล้วก็จะพบว่า $s$ นั้นมีหน่วยเป็นส่วนกลับของ $t$ อย่างแน่นอน เพราะคูณกันอยู่ภายใน $e^{-st}$

พูดถึงสิ่งที่มีมิติเป็นส่วนกลับของเวลาแล้ว สิ่งที่เรารู้จักอย่างดีที่สุดก็คือ ความถี่ นั่นเอง

ถ้างั้นแล้วแสดงว่า $s$ คือความถี่นั่นเอง? ถ้าถามอย่างนี้ก็อาจตอบได้ทั้งใช่และไม่ใช่

เพื่อให้เห็นภาพขอกลับมาที่ปัญหารถติดสปริงและตัวหน่วงที่ยกมาข้างต้น ปัญหานี้ที่จริงแล้วผลเฉลยจะอยู่ในรูปแบบนี้

$\begin{align} x(t) &= A e^{-\alpha t} \sin(\omega t + \theta) \end{align}$

ซึ่งประกอบไปด้วยส่วนของ $\sin(\omega t + \theta)$ ซึ่งแสดงมีค่าวนซ้ำเป็นคาบ และส่วนของ $e^{-\alpha t}$ ซึ่งลดลงตามเวลา หากวาดเป็นกราฟก็จะได้แบบนี้

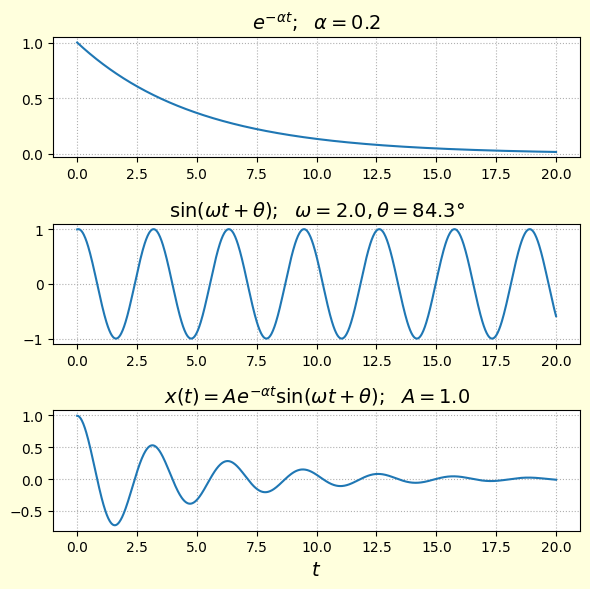
ในที่นี้ $\omega$ ก็คือค่าความถี่ (เรียกให้ถูกกว่าคือ ความถี่เชิงมุม แต่ขอละรายละเอียดเพราะไม่ใช่ประเด็นสำคัญ)

ในขณะที่ $\alpha$ เรียกว่าเป็น ค่าคงตัวของการสลายตัว (decay constant) แบบที่พบได้ในเรื่องการแผ่รังสี เป็นต้น อธิบายอัตราการลดลงตามเวลาของค่าอะไรบางอย่าง (หรืออาจเพิ่มขึ้น ถ้า $\alpha$ เป็นค่าลบ)

ทั้ง $\alpha$ และ $\omega$ ต่างก็เป็นค่าที่อธิบายถึงความเปลี่ยนแปลงเกี่ยวข้องกับเวลา และมีมิติเป็นส่วนกลับของเวลา เช่นเดียวกับ $s$ และถ้าดูต่อไปเราจะเห็นว่าค่าที่เกี่ยวข้องกับความถี่หรือการลดลงตามเวลานี้ถูกเขียนอยู่ในรูปที่บวกหรือลบกับ $s$ อยู่บ่อยๆ

ฉะนั้นสามารถเข้าใจได้ว่าในโลกของตัวแปรลาปลัส $s$ นั้น $s$ แสดงถึงสมบัติที่แสดงถึงการเปลี่ยนแปลงไปตามเวลา ซึ่งนั่นอาจเป็นความถี่ถ้าหากอธิบายถึงอะไรที่เปลี่ยนแปลงแบบมีคาบ และอาจเป็นค่าคงที่การสลายตัว ถ้ากำลังอธิบายถึงสิ่งที่ลดลง (หรือเพิ่มขึ้น) ไปตามเวลา

คำอธิบายนี้อาจจะยังเข้าใจยากอยู่ เพราะตอนนี้ยังไม่ได้แสดงให้เห็นปลายทางว่าแก้ยังไง และ $\alpha$ และ $\omega$ ในที่นี้มาจากไหน ฉะนั้นตอนนี้ถ้าหากอ่านแล้วไม่เข้าใจก็สามารถผ่านไปก็ได้ แต่หากอ่านบทความนี้จนจบจนเห็นภาพรวมแล้วค่อยย้อนกลับมาดูใหม่อาจเห็นภาพได้ชัดขึ้น

สูตรการแปลงที่ใช้บ่อย

การแปลงลาปลัสสามารถทำได้โดยการหาปริพันธ์ ซึ่งก็อาจยุ่งยากอยู่บ้างแต่โดยทั่วไปรูปแบบฟังก์ชันส่วนใหญ่ของปัญหาที่พิจารณามักมีรูปแบบตายตัวอยู่แล้ว จึงใช้วิธีการดูตารางเทียบผลการแปลงที่มีคนคำนวณเอาไว้ให้อยู่แล้วได้

แน่นอนว่าไม่จำเป็นต้องถึงขนาดจำตารางแปลง แค่ดูผ่านๆไว้ว่ามีรูปแบบไหนบ้างเวลาต้องใช้ก็มาเปิดตารางเทียบแล้วแปลงเอา

ในที่นี้จะไม่แสดงวิธีพิสูจน์ แต่ถ้าใครสนใจก็ลองแก้ปริพันธ์ดูว่าได้ตามนั้นจริงหรือเปล่า ก็จะช่วยให้เข้าใจและจำได้ง่ายขึ้นด้วย

ตารางต่อไปนี้ทางซ้ายเป็นฟังก์ชันเดิมซึ่งเป็นฟังก์ชันของ $t$ ส่วนทางขวาเป็นฟังก์ชันหลังแปลงแล้วซึ่งเป็นฟังก์ชันของ $s$

$x(t)$	$X(s)$
$a$ (ค่าคงตัว)	$\begin{align} \frac{a}{s} \end{align}$
$u(t)$ (ฟังก์ชันขั้นบันได)	$\begin{align} \frac{1}{s} \end{align}$
$u(t-\tau)$	$\begin{align} \frac{1}{s} e^{-\tau s} \end{align}$
$\delta(t)$ (ดิแรกเดลตา)	$\begin{align} 1 \end{align}$
$\delta(t-\tau)$	$\begin{align} e^{-\tau s} \end{align}$
$t$	$\begin{align} \frac{1}{s^2} \end{align}$
$t^n$	$\begin{align} \frac{n!}{s^{n+1}} \end{align}$
$\begin{align} \frac{1}{\sqrt{\pi t}} \end{align}$	$\begin{align} \frac{1}{\sqrt{s}} \end{align}$
$\begin{align} \sqrt{\frac{4t}{\pi}} \end{align}$	$\begin{align} \frac{1}{s^{3/2}} \end{align}$
$e^{-\alpha t}$	$\begin{align} \frac{1}{s+\alpha} \end{align}$
$te^{-\alpha t}$	$\begin{align} \frac{1}{(s+\alpha)^2} \end{align}$
$t^ne^{-\alpha t}$	$\begin{align} \frac{n!}{(s+\alpha)^{n+1}} \end{align}$
$1-e^{-\alpha t}$	$\begin{align} \frac{\alpha}{s(s+\alpha)} \end{align}$
$\sin(\omega t)$	$\begin{align} \frac{\omega}{s^2+\omega^2} \end{align}$
$\cos(\omega t)$	$\begin{align} \frac{s}{s^2+\omega^2} \end{align}$
$t\sin(\omega t)$	$\begin{align} \frac{2\omega s}{\left(s^2+\omega^2\right)^2} \end{align}$
$t\cos(\omega t)$	$\begin{align} \frac{s^2-\omega^2}{\left(s^2+\omega^2\right)^2} \end{align}$
$\sin(\omega t + \theta)$	$\begin{align} \frac{\omega\cos\theta + s \sin\theta}{s^2+\omega^2} \end{align}$
$\cos(\omega t + \theta)$	$\begin{align} \frac{s \cos\theta - \omega\sin\theta}{s^2+\omega^2} \end{align}$
$\sinh(\omega t)$	$\begin{align} \frac{\omega}{s^2-\omega^2} \end{align}$
$\cosh(\omega t)$	$\begin{align} \frac{s}{s^2-\omega^2} \end{align}$

เวลาใช้ก็ดูตารางนี้เทียบเพื่อทำการแปลง เช่นจากตารางได้ว่า

$\begin{align} \mathcal{L}[\cosh(\omega t)] = \frac{s}{s^2-\omega^2} \end{align}$

นอกจากนี้จากตารางนี้จะเห็นได้ว่าเมื่อมี $e^{-\alpha t}$ จะทำให้ $s$ กลายเป็น $s+\alpha$ ตรงนี้เป็นสมบัติที่ใช้บ่อย จึงขอเขียนไว้ด้วย

$x(t)$	$X(s)$
$e^{-\alpha t}\sin(\omega t)$	$\begin{align} \frac{\omega}{(s+\alpha)^2+\omega^2} \end{align}$
$e^{-\alpha t}\cos(\omega t)$	$\begin{align} \frac{s+\alpha}{(s+\alpha)^2+\omega^2} \end{align}$
$te^{-\alpha t}\sin(\omega t)$	$\begin{align} \frac{2\omega(s+\alpha)}{\left[\left(s+\alpha\right)^2+\omega^2\right]^2} \end{align}$
$te^{-\alpha t}\cos(\omega t)$	$\begin{align} \frac{\left(s+\alpha\right)^2-\omega^2}{\left[\left.(s+\alpha)\right.^2+\omega^2\right]^2} \end{align}$
$e^{-\alpha t}\sinh(\omega t)$	$\begin{align} \frac{\omega}{(s+\alpha)^2-\omega^2} \end{align}$
$e^{-\alpha t}\cosh(\omega t)$	$\begin{align} \frac{s}{(s+\alpha)^2-\omega^2} \end{align}$

ภาวะเชิงเส้น

ต่อมาขอแนะนำสมบัติที่สำคัญของการแปลงลาปลัส ซึ่งจำเป็นสำหรับนำมาแก้ปัญหาการเคลื่อนที่ของวัตถุที่เป็นเป้าหมายหลักของเราครั้งนี้

การแปลงลาปลัสมีสมบัติที่เรียกว่าภาวะเชิงเส้น (linearity) นั่นคือผลการแปลงลาปลัสของฟังก์ชันบางอย่างที่คูณด้วยค่าคงตัวก็จะเท่ากับค่าคงตัวคูณด้วยผลการแปลงลาปลัสของฟังก์ชันนั้น

$\begin{align} \mathcal{L}[ax(t)] = a\mathcal{L}[x(t)] = aX(s) \end{align}$

โดยในที่นี้ $a$ คือค่าคงตัว

นอกจากนี้การแปลงลาปลัสของ ๒ ฟังก์ชันที่บวกกันก็เท่ากับผลบวกของการแปลงลาปลัสของ ๒ ฟังก์ชันนั้น

$\begin{align} \mathcal{L}[x_1(t)+x_2(t)] = \mathcal{L}[x_1(t)] + \mathcal{L}[x_2(t)] = X_1(s)+X_2(s) \end{align}$

แน่นอนว่าแต่ละฟังก์ชันอาจมีค่าคงตัวคูณอยู่ก็ได้

$\begin{align} \mathcal{L}[a_1x_1(t)+a_2x_2(t)] &= a_1\mathcal{L}[x_1(t)] + a_2\mathcal{L}[x_2(t)] \\ &= a_1X_1(s)+a_2X_2(s) \end{align}$

หรือจะมีกี่ฟังก์ชันก็ได้ ฉะนั้นเขียนในรูปทั่วไปได้ดังนี้

$\begin{align} \mathcal{L}[a_1x_1(t) + a_2x_2(t) + \cdots + a_nx_n(t)] &= a_1\mathcal{L}[x_1(t)] + a_2\mathcal{L}[x_2(t)] + \cdots + a_n\mathcal{L}[x_n(t)] \\ &= a_1X_1(s) + a_2X_2(s) + \cdots + a_nX_n(s) \end{align}$

ยกตัวอย่างการใช้เช่น

$\begin{align} \mathcal{L}[2t + 3e^{-\alpha t}] &= 2\mathcal{L}[t] + 3\mathcal{L}[e^{-\alpha t}] \\ &= \frac{2}{s^2} + \frac{3}{s+\alpha} \end{align}$

เมื่อหาอนุพันธ์

การแปลงลาปลัสมีสมบัติที่สำคัญมากอีกอย่างคือเมื่อนำอนุพันธ์ของฟังก์ชันใดๆมาแปลงลาปลัสจะได้ดังนี้

$\begin{align} \mathcal{L}[\dot{x}(t)] = sX(s) - x(0) \end{align}$

ซึ่งหมายความว่าการหาอนุพันธ์ในโลกของเวลา $t$ เดิมนั้นจะกลายเป็นแค่การคูณ $s$ เมื่ออยู่ในโลกของตัวแปรลาปลัส โดยมีค่า $x(0)$ คือ $x$ ที่เวลาเริ่มต้นอยู่ด้วย ซึ่งก็เป็นแค่ค่าคงตัว ไม่ได้ทำให้ซับซ้อนขึ้นมาก

การพิสูจน์ทำได้ไม่ยากก็เลยขอเขียนลงในนี้ไปด้วย

ก่อนอื่นที่จำเป็นต้องใช้คือสูตรนี้

$\begin{align} \int_{a}^{b}\dot{f}g(t)dt = \left[f(t)g(t)\right]_a^b - \int_{a}^{b}f(t)\dot{g}dt \end{align}$

นำสูตรมาใช้แทนลงไปเพื่อพิสูจน์

$\begin{align} \mathcal{L}[\dot{x}(t)] &= \int_{0}^{\infty}\dot{x}(t)e^{-st}dt \\ &= \left[x(t)e^{-st}\right]_0^\infty + \int_{0}^{\infty}x(t)se^{-st}dt \\ &= x(\infty)e^{-s\times\infty} - x(0)e^{s\times 0} + s\int_{0}^{\infty}x(t)e^{-st}dt \\ &= -x(0) + sX(s) \end{align}$

นอกจากนี้ ต่อไปลองหาอนุพันธ์อันดับสองดู ก็จะได้ว่า

$\begin{align} \mathcal{L}[\ddot{x}(t)] = s^2X(s) - sx(0) - \dot{x}(0) \end{align}$

และอาจนำมาเขียนเป็นสูตรลาปลัสของอนุพันธ์อันดับที่ $n$ ได้เป็น

$\begin{align} \mathcal{L}\left[\frac{d^n}{dt^n}x(t)\right] = s^nX(s) - s^{n-1}x(0) - \cdots - \frac{d^{n-1}}{dt^{n-1}}x(0) \end{align}$

บ่อยครั้งเรามักจะพิจารณาปัญหาที่ค่าตั้งต้นเป็นศูนย์ทั้งหมดซึ่งก็จะได้ว่า

$\begin{align} \mathcal{L}\left[\frac{d^n}{dt^n}x(t)\right] = s^nX(s) \end{align}$

ดังนั้นจึงมองได้ง่ายๆว่าฟังก์ชันที่อยู่ในรูปอนุพันธ์ เมื่อแปลงลาปลัสแล้วก็จะเป็นแค่การคูณ นี่จึงเป็นอะไรที่สำคัญมาก

จากตรงนี้คงเริ่มมองภาพออกกันแล้ว ว่าทำไมการแปลงลาปลัสจึงช่วยให้แก้สมการเชิงอนุพันธ์ได้ง่าย

นั่นก็เพราะเมื่อแปลงลาปลัสแล้ว สมการเชิงอนุพันธ์ก็จะกลายเป็นสมการพหุนามนั่นเอง

เมื่อหาปริพันธ์

สิ่งที่ตรงกันข้ามกับการหาอนุพันธ์ก็คือการหาปริพันธ์ ดังนั้นในขณะที่การแปลงลาปลัสของอนุพันธ์เป็นการคูณ $s$ การแปลงลาปลัสของปริพันธ์ก็จะเท่ากับเป็นการหาร $s$

$\begin{align} \mathcal{L}\left[\int_{0}^{t}x(\tau)d\tau\right] = \frac{1}{s} X(s) \end{align}$

ลองพิสูจน์ดูอย่างง่ายๆได้ โดยสมมุติตัวแปรใหม่ ให้

$\begin{align} h(t) = \int_{0}^{t}x(\tau)d\tau \end{align}$

หาอนุพันธ์ ได้ว่า

$\begin{align} \dot{h}(t) = x(t) \end{align}$

แล้วนำไปแทนก็จะได้ว่า

$\begin{align} X(s) &= \mathcal{L}[x(t)] \\ &= \mathcal{L}[\dot{h}(t)] \\ &= s\mathcal{L}[h(t)] \\ &= s\mathcal{L}\left[\int_{0}^{t}x(\tau)d\tau\right] \end{align}$

ลองนำมาใช้แก้ปัญหาการเคลื่อนที่ของวัตถุ

หลังจากที่ทำความเข้าใจวิธีการแปลงลาปลัสและสมบัติที่จำเป็นแล้ว ก็ขอกลับมาที่ปัญหารถผูกสปริงและตัวหน่วงที่ได้ยกมาข้างต้น

เริ่มจากนำมาทำการแปลงลาปลัส

$\begin{align} m\ddot{x}(t) + c\dot{x}(t) + kx(t) &= 0 \\ \mathcal{L}[m\ddot{x}(t) + c\dot{x}(t) + kx(t)] &= 0 \end{align}$

ใช้สมบัติภาวะเชิงเส้น ได้ว่า

$\begin{align} m\mathcal{L}[\ddot{x}(t)] + c\mathcal{L}[\dot{x}(t)] + k\mathcal{L}[x(t)] = 0 \end{align}$

แล้วใช้สูตรของการแปลงลาปลัสของอนุพันธ์ ได้ว่า

$\begin{align} m[s^2X(s) - sx(0) - \dot{x}(0)] + c[sX(s) - x(0)] + kX(s) &= 0 \\ (ms^2 + cs + k)X(s) - (ms+c)x(0) - m\dot{x}(0) &= 0 \end{align}$

สุดท้ายก็จะได้

$\begin{align} X(s) &= \frac{mx(0)s+cx(0) + m\dot{x}(0)}{ms^2 + cs + k} \end{align}$

ในที่นี้ $x(0)$ และ $\dot{x}(0)$ คือตำแหน่งและความเร็วตั้งต้น เพื่อให้เข้าใจง่ายขอเขียนใหม่เป็น $x_0$ และ $v_0$ กลายเป็น

$\begin{align} X(s) &= \frac{mx_0s+(cx_0 + mv_0)}{ms^2 + cs + k} \end{align}$

ตอนนี้เราได้ $X(s)$ ซึ่งเป็นการแสดงตำแหน่งในโลกของการแปลงลาปลัสแล้ว แต่นี่ยังไม่ใช่เป้าหมายปลายทาง เพราะสิ่งที่เราต้องการจริงๆก็คือ $x(t)$ คือตำแหน่งที่เป็นฟังก์ชันของเวลา เพื่อการนั้นจำเป็นต้องทำการแปลงลาปลัสผกผัน

การแปลงลาปลัสผกผัน

การแปลงลาปลัส (inverse Laplace transform) ผกผันเขียนได้เป็น

$\begin{align} x(t) = \mathcal{L}^{-1}[X(s)] \end{align}$

การแปลงลาปลัสผกผันนั้นก็มีนิยามการคำนวณอยู่ แต่ว่าค่อนข้างซับซ้อนและโดยทั่วไปแล้วไม่จำเป็นต้องใช้ ในที่นี้จึงจะขอละไว้ไม่เขียนถึงเพื่อไม่ให้รู้สึกยุ่งยากเกินไป แต่วิธีที่มักใช้ในการแปลงลาปลัสผกผันก็คือเทียบตารางแปลง เหมือนอย่างที่ใช้ในการแปลงลาปลัส แค่มองกลับด้านเท่านั้น

เช่นจากตารางแปลงเรารู้ได้ว่า

$\begin{align} \mathcal{L}[\sin\omega t] = \frac{\omega^2}{s^2+\omega^2} \end{align}$

ดังนั้นก็จะได้ว่า

$\begin{align} \mathcal{L}^1\left[ \frac{\omega^2}{s^2+\omega^2} \right] = \sin\omega t \end{align}$

ทีนี้มาพิจารณาปัญหารถติดสปริงและตัวหน่วงต่อ เพื่อที่จะแก้จำเป็นต้องจัดรูปให้อยู่ในรูปแบบที่ตรงกับในตารางแปลงเพื่อจะทำการแปลงกลับได้

$\begin{align} X(s) &= \frac{mx_0s+(cx_0 + mv_0)}{ms^2 + cs + k} \\ &= x_0 \frac{s+(c/m + v_0/x_0)}{s^2 + (c/m)s + k/m} \\ &= x_0 \frac{(s+c/2m) - c/2m + (c/m + v_0/x_0)}{(s+c/2m)^2 - (c/2m)^2 + k/m} \\ &= x_0 \frac{s+c/2m}{(s+c/2m)^2 + \sqrt{k/m - (c/2m)^2}^2} \\ &+ x_0 \frac{c/2m + v_0/x_0}{\sqrt{k/m - (c/2m)^2}} \frac{\sqrt{k/m - (c/2m)^2}}{(s+c/2m)^2 + \sqrt{k/m - (c/2m)^2}^2} \end{align}$

ทำการแทน

$\begin{align} \alpha = c/2m \end{align}$

และ

$\begin{align} \omega = \sqrt{k/m - (c/2m)^2} \end{align}$

แล้วเขียนใหม่ได้เป็น

$\begin{align} X(s) &= x_0 \frac{s+\alpha}{(s+\alpha)^2 + \omega} + x_0 \frac{\alpha + v_0/x_0}{\omega} \frac{\omega}{(s+\alpha)^2 + \omega^2} \end{align}$

จากนั้นเปิดตารางดูจะเห็นว่า

$\begin{align} \mathcal{L}^{-1}\left[ \frac{s+\alpha}{(s+\alpha)^2+\omega^2} \right] = e^{-\alpha t} \cos(\omega t) \\ \mathcal{L}^{-1}\left[ \frac{\omega}{(s+\alpha)^2+\omega^2} \right] = e^{-\alpha t} \sin(\omega t) \end{align}$

ฉะนั้นแล้วเราก็ทำการแปลงลาปลัสกลับได้ผลดังนี้

$\begin{align} x(t) &= x_0e^{-\alpha t} \cos(\omega t) + x_0\frac{\alpha + v_0/x_0}{\omega}e^{-\alpha t} \sin(\omega t) \\ &= x_0e^{-\alpha t} \left(\cos(\omega t) + \frac{\alpha + v_0/x_0}{\omega}\sin(\omega t) \right) \end{align}$

จากตรงนี้ถ้าใช้สมบัติของตรีโกณมิติก็จะสามารถเขียนได้ในรูป

$\begin{align} x(t) &= A e^{-\alpha t} \sin(\omega t + \theta) \end{align}$

โดยในที่นี้

$\begin{align} A &= x_0 \sqrt{1 + \left( \frac{\alpha + v_0/x_0}{\omega} \right)^2} \\ \theta &= \text{atan2}\left(\omega, \alpha + \frac{v_0}{x_0}\right) \end{align}$

ซึ่งผลที่ได้ก็เป็นไปตามกราฟและภาพเคลื่อนไหวที่ได้ลงไว้แล้วข้างต้น มีส่วน $e^{-\alpha t}$ ซึ่งเป็นการลดลงแบบเอกซ์โพเนนเชียล และส่วน $\sin(\omega t + \theta)$ ที่สั่นเป็นคาบ จึงได้เป็นการสั่นแบบหน่วงจนผ่านไปนานก็หยุดลงในที่สุด

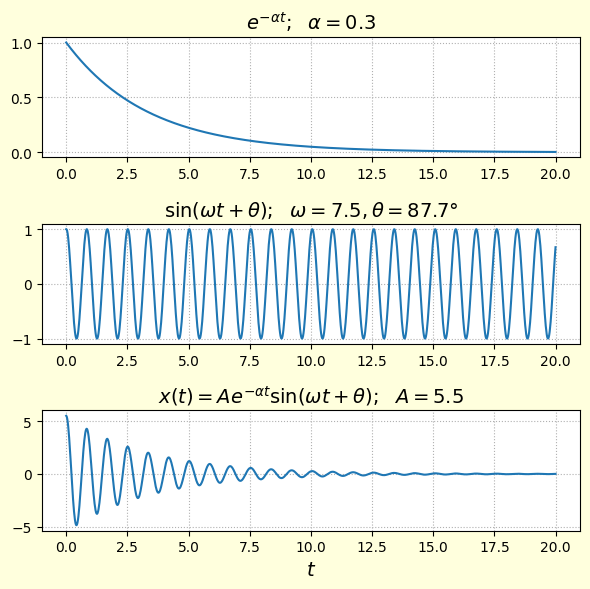
เพียงแต่ว่าในที่นี้ $\omega = \sqrt{k/m - (c/2m)^2}$ อาจมีค่าเป็น 0 หรือติดลบได้หากค่าคงตัวสปริงต่ำมาก $k \le c^2/4m$ กรณีนี้จะเกิดการหน่วงวิกฤต หรือหน่วงเกิน ไม่เกิดการสั่นเป็นคาบ

นอกจากนี้แล้ว ถ้าหากไม่มีตัวหน่วง นั่นคือ $c = 0$ จะได้ว่า $\alpha = 0$ แล้วส่วนเอกซ์โพเนนเชียลก็จะหายไป ได้ว่า

$\begin{align} x(t) &= A \sin(\omega t + \theta) \end{align}$

ซึ่งก็คือการสั่นแบบฮาร์มอนิกอย่างง่าย ซึ่งจะสั่นแบบนี้ไปตลอดกาล

จากตัวอย่างนี้จะเห็นว่าเราสามารถใช้การแปลงลาปลัสมาช่วยในการแก้สมการเชิงอนุพันธ์เช่นในปัญหาทางฟิสิกส์ได้ โดยการแปลงลาปลัสแล้วจัดรูปทำอะไรต่างๆในโลกของตัวแปรลาปลัส เสร็จแล้วก็แปลงกลับด้วยการแปลงลาปลัสผกผัน

อย่างไรก็ตาม ถ้าปัญหาซับซ้อน การแปลงลาปลัสผกผันก็จะยิ่งทำได้ยากขึ้น บางทีอาจไม่สามารถแปลงกลับได้เสมอไป

เพียงแต่ว่าการแปลงกลับอาจไม่ใช่สิ่งจำเป็นเสมอไป แม้ว่าค่าในโลกของตัวแปรลาปลัสจะไม่ได้เป็นอะไรที่เห็นภาพชัดเท่าโลกของเวลาที่เราคุ้นเคย แต่ก็มีส่วนที่สามารถตีความทั้งๆแบบนั้นได้เช่นกัน คล้ายกับการวิเคราะห์สมบัติเชิงความถี่ในการแปลงฟูรีเย

ทฤษฎีบทค่าท้ายสุด

สมบัติอีกอย่างหนึ่งของลาปลัสที่สำคัญและใช้ได้บ่อยก็คือสิ่งที่เรียกว่า ทฤษฎีบทค่าท้ายสุด (final value theorem) ซึ่งอธิบายว่า

$\begin{align} x(\infty) = \lim_{s \to 0}sX(s) \end{align}$

นั่นคือค่าที่เมื่อเวลา $t$ ผ่านไปนานเป็นอนันต์จะหาได้ง่ายด้วยการแทนค่า $s$ เป็น 0 โดยไม่จำเป็นต้องแปลงลาปลัสกลับเลย

เพียงแต่มีเงื่อนไขคือว่าค่า $x_0$ จะต้องลู่เข้าที่ค่าหนึ่งเมื่อเวลาผ่านไปนาน ซึ่งระบบที่เราพิจารณาโดยทั่วไปก็เป็นแบบนั้นอยู่แล้ว ถ้าค่าลู่ออกก็ไม่สามารถหาค่าได้อยู่แล้ว

สำหรับตัวอย่างการใช้ ลองเอามาใช้กับปัญหารถติดสปริงและตัวหน่วงที่อธิบายมาข้างต้น เพื่อหาตำแหน่งของรถหลังจากที่เวลาผ่านไปนานมาก

$\begin{align} x(\infty) &= \lim_{s \to 0}s\frac{mx_0s+(cx_0 + mv_0)}{ms^2 + cs + k} \\ &= \lim_{s \to 0}\frac{mx_0s^2+(cx_0 + mv_0)s}{ms^2 + cs + k} \\ &= 0 \end{align}$

จะเห็นได้ว่าไม่ว่าจะเริ่มต้นที่ตำแหน่งไหนหรือมีความเร็วเริ่มต้นเท่าไหร่ก็ตาม สุดท้ายรถก็จะมาหยุดสิ่งที่ตำแหน่ง 0

เพื่อให้เห็นภาพมากขึ้น ขอยกตัวอย่างเพิ่มเติม โดยเพิ่มแรง $f_0$ เป็นค่าคงตัวเข้ามายังตัวรถ ซึ่งหมายความว่านอกจากจะมีแรงจากสปริงและตัวหน่วงแล้วเรายังออกแรงเสริมคงที่ให้กับรถอีก ก็จะได้สมการการเคลื่อนที่เป็นแบบนี้

$\begin{align} m\ddot{x}(t) + c\dot{x}(t) + kx(t) - f_0 = 0 \end{align}$

นำมาแปลงลาปลัส

$\begin{align} m\mathcal{L}[\ddot{x}(t)] + c\mathcal{L}[\dot{x}(t)] + k\mathcal{L}[x(t)] - \mathcal{L}[f_0] &= 0 \\ m[s^2X(s) - sx(0) - \dot{x}(0)] + c[sX(s) - x(0)] + kX(s) - \frac{f_0}{s} &= 0 \\ (ms^2 + cs + k)X(s) - (ms+c)x(0) - m\dot{x}(0) - \frac{f_0}{s} &= 0 \end{align}$

แล้วสุดท้ายจะได้ว่า

$\begin{align} X(s) &= \frac{mx(0)s+cx(0) + m\dot{x}(0) + f_0/s}{ms^2 + cs + k} \end{align}$

หาค่าที่เวลาอนันต์ด้วยทฤษฎีบทค่าท้ายสุด

$\begin{align} x(\infty) &= \lim_{s \to 0}sX(s) \\ &= \lim_{s \to 0}s\frac{mx_0s+cx_0 + mv_0 + f_0/s}{ms^2 + cs + k} \\ &= \lim_{s \to 0}\frac{mx_0s^2+cx_0s + mv_0s + f_0}{ms^2 + cs + k} \\ &= \frac{f_0}{k} \end{align}$

ซึ่งก็เป็นไปตามระยะยืดของสปริงที่ควรได้เมื่อออกแรงค่าหนึ่งๆ ซึ่งตอนที่เริ่มดึงอาจจะมีการสั่น แต่สุดท้ายก็จะมาหยุดนิ่งอยู่ที่ระยะ $f_0/k$ ในที่สุด

เพียงแต่ให้ระวังว่าในที่นี้จะเห็นว่าต่อให้แทน $c=0$ ก็ยังได้ $f_0/k$ ซึ่งขัดต่อความเป็นจริงซึ่งเรารู้ว่าถ้าไม่มีแรงหน่วงระบบจะสั่นตลอดไปไม่ลู่เข้าค่าใด ดังนั้นจึงแสดงให้เห็นว่ากรณีที่ไม่ลู่เข้า ทฤษฎีบทค่าท้ายสุดนี้จะไม่เป็นจริง ไม่สามารถใช้ได้ ฉะนั้นก่อนใช้ต้องพิสูจน์ให้แน่ว่าค่าจะลู่เข้า

สำหรับการแปลงลาปลัสผกผันกลับเพื่อหารูปทั่วไปของ $x(t)$ ในที่นี้จะไม่แสดงให้ดู แต่ก็สามารถทำได้ อาจไปลองทำดูกันได้หากสนใจ ถ้าแก้แล้วลองแทน $x_0=0, v_0=0, f_0=200, k=20, m=500, c=40$ ก็จะได้กราฟแสดงตำแหน่งดังนี้

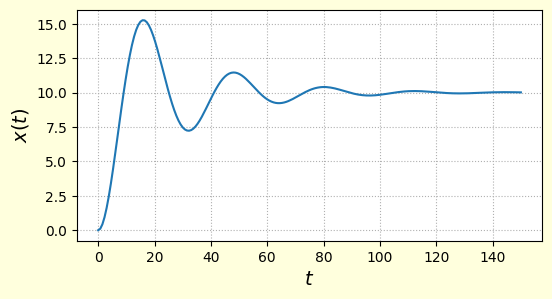
จะเห็นว่าลู่เข้าที่ $f_0/k = 200/20 = 10$ ตามที่คำนวณได้

สรุปส่งท้าย

การแปลงลาปลัสสามารถนำมาใช้เพื่อช่วยให้การแก้ปัญหาทางฟิสิกส์ง่ายขึ้นได้
การแปลงลาปลัสเป็นการแปลงค่าที่พิจารณาจากโลกของเวลา t ไปเป็นโลกของตัวแปรลาปลัส s
การหาอนุพันธ์ในโลกของเวลา t เป็นการคูณ s ในโลกของตัวแปรลาปลัส
การหาปริพันธ์ในโลกของเวลา t เป็นการหาร s ในโลกของตัวแปรลาปลัส
ฉะนั้นจึงทำให้สมการเชิงอนุพันธ์กลายเป็นสมหารพหุนาม จึงแก้ได้สะดวกขึ้นมาก
ตัวแปรลาปลัส s นั้นมีมิติเป็นส่วนกลับของเวลา t สามารถมองว่าเป็นค่าความถี่หรือค่าคงตัวของการสลายตัว
เราสามารถแปลงค่าจากโลกของตัวแปรลาปลัส s กลับมาเป็นค่าในโลกของเวลา t ที่เราคุ้นเคยได้โดยทำการแปลงลาปลัสผกผัน
เราอาจสามารถวิเคราะห์ค่าในโลกของตัวแปรลาปลัสได้โดยไม่ต้องแปลงกลับ ถ้าเข้าใจความหมาย รู้ว่าตีความอย่างไร
การแปลงลาปลัสผกผันมักทำโดยการจัดรูปให้อยู่ในรูปตามตารางแปลง มากกว่าที่จะคำนวณโดยตรง
หากสนใจแค่ค่าที่เวลาอนันต์ในระบบลู่เข้า สามารถใช้ทฤษฎีบทค่าท้ายสุดหาได้โดยไม่ต้องแปลงลาปลัสผกผันกลับ

เรื่องของการแปลงลาปลัสยังมีรายละเอียดอีกมากมาย ที่อธิบายไปนี้เป็นแค่เบื้องต้น เพื่อให้พอเห็นภาพว่าการแปลงลาปลัสมีเอาไว้ทำอะไร มีวิธีการใช้อย่างไร หากใครสนใจก็สามารถศึกษาเพิ่มเติมกันต่อไปได้

อ้างอิง

วิดีโอ

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

ดูสถิติของหน้านี้

หมวดหมู่

-- คณิตศาสตร์

ไม่อนุญาตให้นำเนื้อหาของบทความไปลงที่อื่นโดยไม่ได้ขออนุญาตโดยเด็ดขาด หากต้องการนำบางส่วนไปลงสามารถทำได้โดยต้องไม่ใช่การก๊อปแปะแต่ให้เปลี่ยนคำพูดเป็นของตัวเอง หรือไม่ก็เขียนในลักษณะการยกข้อความอ้างอิง และไม่ว่ากรณีไหนก็ตาม ต้องให้เครดิตพร้อมใส่ลิงก์ของทุกบทความที่มีการใช้เนื้อหาเสมอ

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

φυβλαςのβλογ
บล็อกของ phyblas

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

หมวดหมู่

~ เกี่ยวกับเรา ~

สารบัญ

บทความแบ่งตามหมวด

ค้นหาบทความ

บทความล่าสุด

บทความแนะนำ

บทความแต่ละเดือน

2025年

2024年

2023年

2022年

2021年

ค้นบทความเก่ากว่านั้น

ไทย

日本語

中文

φυβλαςのβλογบล็อกของ phyblas

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

หมวดหมู่

~ เกี่ยวกับเรา ~

สารบัญ

บทความแบ่งตามหมวด

ค้นหาบทความ

บทความล่าสุด

บทความแนะนำ

บทความแต่ละเดือน

2025年

2024年

2023年

2022年

2021年

ค้นบทความเก่ากว่านั้น

ไทย

日本語

中文

φυβλαςのβλογ
บล็อกของ phyblas

　 ค้นหาบทความ

　 บทความล่าสุด

　 บทความแนะนำ