[python] การใช้ฟังก์ชัน cdist, pdist และ squareform ใน scipy เพื่อหาระยะห่างระหว่างจุดต่างๆ
เขียนเมื่อ 2018/07/22 19:17
แก้ไขล่าสุด 2021/09/28 16:42
บทความนี้เขียนขึ้นเพื่อเสริมเนื้อหาการเรียนรู้ของเครื่อง โดยจะแนะนำฟังก์ชันของ scipy ที่เกี่ยวกับการหาระยะห่างระหว่างจุด
ในการเขียนโปรแกรมการเรียนรู้ของเครื่อง การคำนวณระยะห่างระหว่างจุดข้อมูลมีความสำคัญ ถูกใช้บ่อยในหลายเทคนิค เช่น วิธีการเพื่อนบ้านใกล้สุด k ตัว, วิธีการ k เฉลี่ย และเทคนิคที่ต้องคำนวณฟังก์ชันเคอร์เนล
ฟังก์ชันที่จะแนะนำคือ cdist, pdist และ squareform ซึ่งอยู่ในมอดูลย่อย scipy.spatial.distance ของ scipy
pdist
ฟังก์ชัน pdist มีไว้หาระยะห่างระหว่างจุดต่างๆที่อยู่ในอาเรย์
ระยะทางที่เราคุ้นเคยกันทั่วไปนั้นเรียกว่าระยะทางแบบยูคลิด (欧几里得距离, Euclidean distance) คือรากที่สองของผลรวมค่ายกกำลังสอง
..(1)
ค่าที่ใช้คำนวณใน pdist ต้องเป็นอาเรย์สองมิติของตำแหน่งจุด
ผลที่ได้จะเป็นการจับคู่ทุกจุดที่ป้อนเข้าไปแล้วหาระยะห่างทีละคู่ ดังนั้นถ้ามี n ตัวจะได้ออกมาเป็นจำนวน (n*(n-1))/2
เช่นถ้าใส่อาเรย์ [[x1,y1],[x2,y2],[x3,y3]] แล้วผลที่ได้จะเป็น [((x1-x2)**2+(y1-y2)**2)**0.5, ((x1-x3)**2+(y1-y3)**2)**0.5, ((x2-x3)**2+(y2-y3)**2)**0.5]
ตัวอย่าง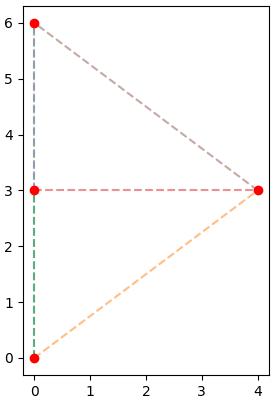
นอกจากจะหาระยะทางแบบยูคลิดแล้วในโลกคณิตศาสตร์มีวิธีในการวัดระยะทางอยู่หลากหลายรูปแบบ
ยกตัวอย่างเช่นระยะทางแมนฮัตตัน (曼哈顿距离, Manhattan distance) เป็นระยะทางที่เกิดจากการเอาระยะทางแต่ละมิติมาบวกกันแบบกำลังหนึ่ง
..(2)
ถ้าจะคำนวณระยะทางแบบอื่นที่ไม่ใช่ยูคลิดธรรมดาให้ใส่ระบุรูปแบบลงไป
เช่นถ้าต้องการระยะทางแมนฮัตตันสามารถคำนวณโดยใส่รูปแบบระยะทางเป็น cityblock
..(3)
โดย p เป็นเลขชี้กำลัง จะมีค่าเท่าไหร่ก็ได้ ถ้า p=1 จะเป็นแมนฮัตตัน ถ้า p=2 จะเป็นยูคลิด
ถ้าต้องการระยะทางแบบมินคอฟสกีก็ให้ใส่รูปแบบเป็น minkowski และต้องระบุค่า p เป็นเลขยกกำลังที่ต้องการ (ถ้าไม่ระบุจะเป็น p=2 คือเป็นยูคลิด)
ที่จริงจะคำนวณระยะทางยูคลิดแบบธรรมดา (euclidean) แล้วค่อยมายกกำลังสองอีกที pdist(X,'euclidean')**2 แบบนี้ก็ได้ แต่ทำแบบนี้จะใช้เวลามากกว่าการใช้ pdist(X,'sqeuclidean') เล็กน้อย
ดังนั้นหากต้องการระยะทางยูคลิดยกกำลังสองอยู่แล้วใช้ pdist(X,'sqeuclidean') เป็นทางเลือกที่ดีที่สุด
นอกจากนี้ยังมีระยะทางชนิดอื่นๆอีกมากมาย ที่เหลือส่วนใหญ่เป็นคณิตศาสตร์ระดับสูงขึ้นไป สำหรับใช้เฉพาะทาง
ระยะทางชนิดต่างๆที่สามารถคำนวณได้ด้วย pdist ดูได้จาก
https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.pdist.html
squareform
ส่วน squareform จะเป็นตัวแปลงระยะห่างไปอยู่ในรูปแบบของเมทริกซ์สมมาตร
ตัวอย่าง
เมื่อใช้คู่กับ pdist ก็จะได้ระยะห่างของแต่ละคู่จุดออกมาเป็นเมทริกซ์
นอกจากนี้ squareform ยังสามารถทำในสิ่งตรงข้าม คือแปลงเมทริกซ์สมมาตรกลับมาเป็นอาเรย์ของระยะทาง
ดังนั้น squareform(squareform(X)) จะได้เท่ากับ X
อย่างไรก็ตาม pdist มีไว้หาระยะห่างระหว่างสมาชิกในกลุ่มเดียวกันเท่านั้น ถ้าต้องการหาระยะห่างระหว่างจุดคนละกลุ่มให้ใช้ cdist
cdist
cdist เป็นฟังก์ชันสำหรับหาระยะห่างระหว่างจุดภายในอาเรย์สองชุดที่ป้อนเข้าไป โดยจะจับคู่แล้วแสดงผลออกมาเป็นเมทริกซ์
ถ้าใช้ cdist(X,X) จะกลายเป็นการหาระยะของจุดข้อมูลกลุ่มเดียวกัน จึงจะได้ผลเหมือนกับการใช้ squareform(pdist(X))
ตัวอย่าง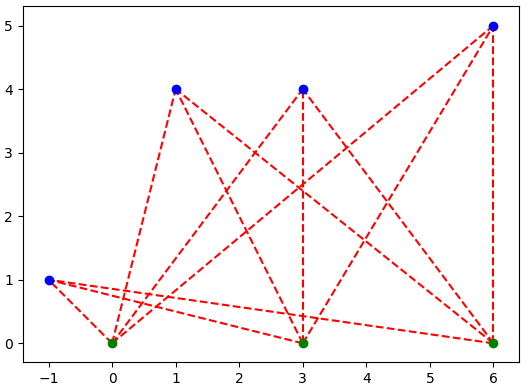
การคำนวณแบบเดียวกับที่ cdist ทำนั้น จริงๆแล้วหากให้เขียนฟังก์ชันขึ้นเองอาจเขียนได้เป็น
สรุปโดยรวมแล้ว เมื่อต้องการหาระยะห่างระหว่างจุด ใช้ pdist หรือ cdist แทนที่จะเขียนเอง จะประหยัดเวลาได้มาก
ในการเขียนโปรแกรมการเรียนรู้ของเครื่อง การคำนวณระยะห่างระหว่างจุดข้อมูลมีความสำคัญ ถูกใช้บ่อยในหลายเทคนิค เช่น วิธีการเพื่อนบ้านใกล้สุด k ตัว, วิธีการ k เฉลี่ย และเทคนิคที่ต้องคำนวณฟังก์ชันเคอร์เนล
ฟังก์ชันที่จะแนะนำคือ cdist, pdist และ squareform ซึ่งอยู่ในมอดูลย่อย scipy.spatial.distance ของ scipy
pdist
ฟังก์ชัน pdist มีไว้หาระยะห่างระหว่างจุดต่างๆที่อยู่ในอาเรย์
ระยะทางที่เราคุ้นเคยกันทั่วไปนั้นเรียกว่าระยะทางแบบยูคลิด (欧几里得距离, Euclidean distance) คือรากที่สองของผลรวมค่ายกกำลังสอง
..(1)
ค่าที่ใช้คำนวณใน pdist ต้องเป็นอาเรย์สองมิติของตำแหน่งจุด
ผลที่ได้จะเป็นการจับคู่ทุกจุดที่ป้อนเข้าไปแล้วหาระยะห่างทีละคู่ ดังนั้นถ้ามี n ตัวจะได้ออกมาเป็นจำนวน (n*(n-1))/2
เช่นถ้าใส่อาเรย์ [[x1,y1],[x2,y2],[x3,y3]] แล้วผลที่ได้จะเป็น [((x1-x2)**2+(y1-y2)**2)**0.5, ((x1-x3)**2+(y1-y3)**2)**0.5, ((x2-x3)**2+(y2-y3)**2)**0.5]
ตัวอย่าง
import numpy as np
from scipy.spatial.distance import pdist
X = np.array([[0.,0],[0,3],[4,3],[0,6]])
print(pdist(X))
# ได้ [ 3. 5. 6. 4. 3. 5.]
นอกจากจะหาระยะทางแบบยูคลิดแล้วในโลกคณิตศาสตร์มีวิธีในการวัดระยะทางอยู่หลากหลายรูปแบบ
ยกตัวอย่างเช่นระยะทางแมนฮัตตัน (曼哈顿距离, Manhattan distance) เป็นระยะทางที่เกิดจากการเอาระยะทางแต่ละมิติมาบวกกันแบบกำลังหนึ่ง
..(2)
ถ้าจะคำนวณระยะทางแบบอื่นที่ไม่ใช่ยูคลิดธรรมดาให้ใส่ระบุรูปแบบลงไป
เช่นถ้าต้องการระยะทางแมนฮัตตันสามารถคำนวณโดยใส่รูปแบบระยะทางเป็น cityblock
pdist(X,'cityblock')
#ได้ array([ 3., 7., 6., 4., 3., 7.])..(3)
โดย p เป็นเลขชี้กำลัง จะมีค่าเท่าไหร่ก็ได้ ถ้า p=1 จะเป็นแมนฮัตตัน ถ้า p=2 จะเป็นยูคลิด
ถ้าต้องการระยะทางแบบมินคอฟสกีก็ให้ใส่รูปแบบเป็น minkowski และต้องระบุค่า p เป็นเลขยกกำลังที่ต้องการ (ถ้าไม่ระบุจะเป็น p=2 คือเป็นยูคลิด)
print(pdist(X,'minkowski',p=3))
# ได้ array([ 3. , 4.49794145, 6. , 4. , 3. , 4.49794145])ที่จริงจะคำนวณระยะทางยูคลิดแบบธรรมดา (euclidean) แล้วค่อยมายกกำลังสองอีกที pdist(X,'euclidean')**2 แบบนี้ก็ได้ แต่ทำแบบนี้จะใช้เวลามากกว่าการใช้ pdist(X,'sqeuclidean') เล็กน้อย
ดังนั้นหากต้องการระยะทางยูคลิดยกกำลังสองอยู่แล้วใช้ pdist(X,'sqeuclidean') เป็นทางเลือกที่ดีที่สุด
นอกจากนี้ยังมีระยะทางชนิดอื่นๆอีกมากมาย ที่เหลือส่วนใหญ่เป็นคณิตศาสตร์ระดับสูงขึ้นไป สำหรับใช้เฉพาะทาง
ระยะทางชนิดต่างๆที่สามารถคำนวณได้ด้วย pdist ดูได้จาก
https://docs.scipy.org/doc/scipy/reference/generated/scipy.spatial.distance.pdist.html
squareform
ส่วน squareform จะเป็นตัวแปลงระยะห่างไปอยู่ในรูปแบบของเมทริกซ์สมมาตร
ตัวอย่าง
from scipy.spatial.distance import squareform
print(squareform([1,2,3,4,5,6]))[[0 1 2 3]
[1 0 4 5]
[2 4 0 6]
[3 5 6 0]]เมื่อใช้คู่กับ pdist ก็จะได้ระยะห่างของแต่ละคู่จุดออกมาเป็นเมทริกซ์
X = np.array([[0.,0],[0,3],[4,3],[0,6]])
print(squareform(pdist(X)))[[ 0. 3. 5. 6.]
[ 3. 0. 4. 3.]
[ 5. 4. 0. 5.]
[ 6. 3. 5. 0.]]นอกจากนี้ squareform ยังสามารถทำในสิ่งตรงข้าม คือแปลงเมทริกซ์สมมาตรกลับมาเป็นอาเรย์ของระยะทาง
ดังนั้น squareform(squareform(X)) จะได้เท่ากับ X
อย่างไรก็ตาม pdist มีไว้หาระยะห่างระหว่างสมาชิกในกลุ่มเดียวกันเท่านั้น ถ้าต้องการหาระยะห่างระหว่างจุดคนละกลุ่มให้ใช้ cdist
cdist
cdist เป็นฟังก์ชันสำหรับหาระยะห่างระหว่างจุดภายในอาเรย์สองชุดที่ป้อนเข้าไป โดยจะจับคู่แล้วแสดงผลออกมาเป็นเมทริกซ์
ถ้าใช้ cdist(X,X) จะกลายเป็นการหาระยะของจุดข้อมูลกลุ่มเดียวกัน จึงจะได้ผลเหมือนกับการใช้ squareform(pdist(X))
ตัวอย่าง
from scipy.spatial.distance import cdist
X1 = np.array([[0.,0],[3,0],[6,0]])
X2 = np.array([[1.,4],[3,4],[6,5],[-1,1]])
print(cdist(X1,X2,'sqeuclidean'))[[ 17. 25. 61. 2.]
[ 20. 16. 34. 17.]
[ 41. 25. 25. 50.]]
การคำนวณแบบเดียวกับที่ cdist ทำนั้น จริงๆแล้วหากให้เขียนฟังก์ชันขึ้นเองอาจเขียนได้เป็น
np.sum([(X2-x)**2 for x in X1],2)((X1[:,None]-X2[None])**2).sum(2)สรุปโดยรวมแล้ว เมื่อต้องการหาระยะห่างระหว่างจุด ใช้ pdist หรือ cdist แทนที่จะเขียนเอง จะประหยัดเวลาได้มาก