numpy & matplotlib เบื้องต้น บทที่ ๓๓: การวาดในระบบพิกัดเชิงขั้ว
เขียนเมื่อ 2016/06/12 16:14
แก้ไขล่าสุด 2022/07/21 20:37
ในบทที่ผ่านๆมาเราทำทุกอย่างในระบบพิกัดฉากมาโดยตลอด เพราะเป็นระบบพื้นฐานที่ง่ายที่สุด
แต่หากต้องการทำให้ทุกอย่างอยู่ในระบบพิกัดเชิงขั้ว matplotlib ก็สามารถทำได้เช่นกัน
วาดกราฟในพิกัดเชิงขั้ว
การเขียนให้อยู่ในรูปพิกัดเชิงขั้วทำได้โดยกำหนดที่ตัว axes โดยตอนสร้าง axes ขึ้นมาให้ใส่คีย์เวิร์ดว่า polar=1 หรือไม่ก็ projection='polar'
จากนั้นเวลาวาดกราฟก็ใช้คำสั่งวาดแบบเดียวกับที่ใช้กันมาในระบบพิกัดฉาก แต่ค่าที่ต้องใส่จะใช้อาร์กิวเมนต์ตัวแรกเป็นค่ามุม และตัวหลังเป็นระยะห่างจากใจกลาง
ค่ามุมมีหน่วยเป็นเรเดียน ดังนั้นหากจะใส่หน่วยเป็นองศาก็ต้องแปลงก่อน โดยอาจใช้ฟังก์ชัน np.radians ช่วย
ตัวอย่าง วาดกราฟซึ่งมีระยะห่างจากใจกลางเพิ่มตามมุม
แค่นี้ก็ออกมาเป็นพิกัดเชิงขั้วอย่างง่ายแล้ว
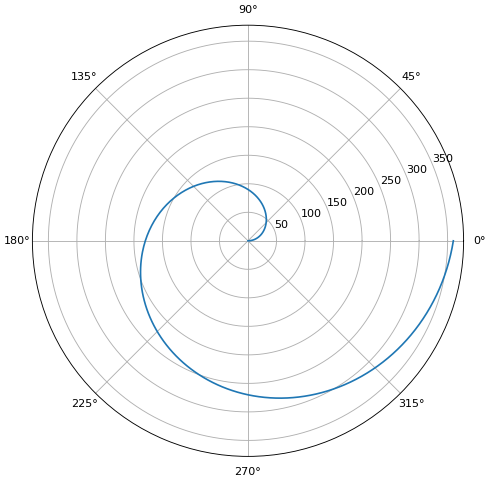
ตรงนี้หากเราตัดบรรทัด plt.axes(polar=1) ออกไปแล้วลองวาดใหม่ผลที่ได้ก็จะได้เป็นกราฟเส้นตรงธรรมดา
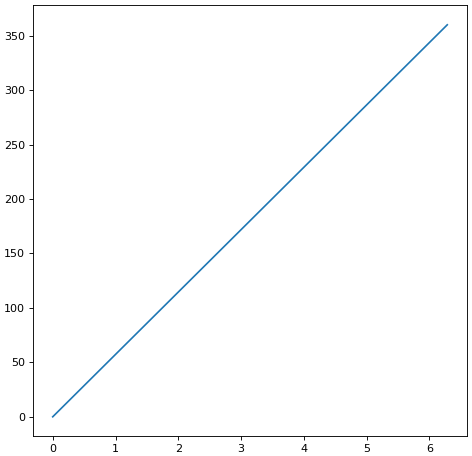
โดยในที่นี้แกนนอนคือมุม แกนตั้งคือระยะห่างจากใจกลาง จะเห็นว่าดูแล้วก็เหมือนกับว่าพิกัดเชิงขั้วคือการเอากราฟนี้ไปวาดใหมโดย เปลี่ยนแกนนอนเป็นค่ามุมและแกนตั้งเป็นระยะห่างจากใจกลางนั่นเอง
พิกัดเชิงขั้วถ้าหากวนครบ 360 องศาก็จะกลับมาอยู่ที่มุมเดิม ดังนั้นจะเห็นกราฟที่วนซ้อนกันไปเรื่อยๆได้ กราฟ cos ธรรมดาในระบบพิกัดฉากพอมาอยู่ในระบบพิกัดเชิงขั้วก็กลายเป็นลวดลายสวยงามแบบ นี้ได้
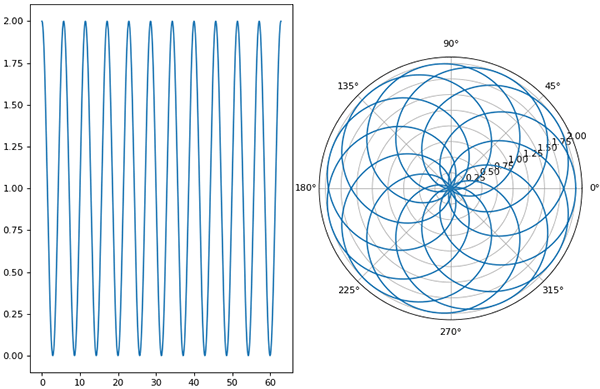
ที่จริงแล้วหากไม่ต้องการวาดให้อยู่ในรูปพิกัดเชิงขั้วเราอาจจะแปลงจาก r,θ เป็น x,y เองก็ได้ด้วยการคำนวณโดย x = rcosθ, y = rsinθ
ลองทำการคำนวณแปลงเป็น x,y แล้วพล็อตกราฟธรรมดาก็จะได้กราฟแบบเดียวกัน เพียงแต่อยู่ในระบบพิกัดฉาก
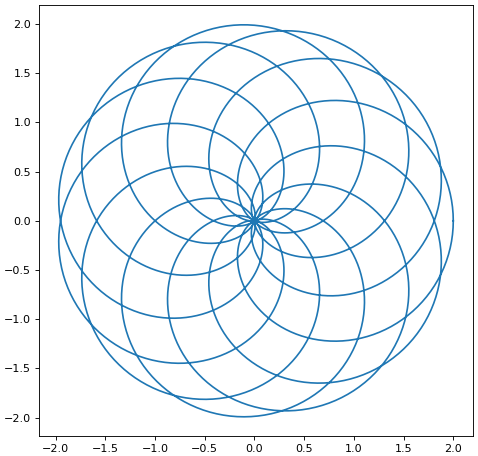
การปรับแต่ง
โดยหลักแล้วกราฟในพิกัดเชิงขั้วก็สามารถปรับแต่งอะไรต่างๆได้ในลักษณะคล้ายกับของพิกัดฉาก แต่ก็มีความแตกต่างออกไปบ้างเล็กน้อย
ลองดูตัวอย่างเช่นการแก้ตำแหน่งขีดบอกค่านั้นทำได้โดยใช้ฟังก์ชัน plt.xticks กับ plr.yticks หรือด้วยเมธอด set_xticks กับ set_yticks ได้เหมือนกัน โดย xticks ในที่นี้จะเป็นขีดของมุม ส่วน yticks เป็นขีดของระยะห่างจากใจกลาง
จะเห็นว่าค่า xticks ที่ป้อนเข้าไปนั้นต้องเป็นหน่วยเรเดียน แต่พอแสดงผลออกมาจริงๆกลับถูกเปลี่ยนให้เป็นหน่วยองศาโดยอัตโนมัติ
การเปลี่ยนการแสดงผลให้เป็นหน่วยเรเดียนหรือเป็นอะไรอื่นๆอาจทำได้โดยใช้ set_xticklabels
ลองพิมพ์เพิ่มลงไปตามนี้จะได้ค่าเป็นหน่วยเรเดียน
หรือลองใช้ latex เพื่อให้ดูสวยขึ้น เช่น พิมพ์ตามนี้เพิ่มเข้าไป
สำหรับค่าขีดบอกตำแหน่งในแนวรัศมีนั้นนอกจากจะปรับได้ด้วย set_yticks แล้วยังอาจใช้ set_rgrids ซึ่งจะดีกว่าตรงที่สามารถตั้งตำแหน่งที่จะวางได้ด้วย โดยใส่คีย์เวิร์ด angle หน่วยเป็นองศา
นอกจากนี้หากต้องการปรับแค่ตำแหน่งมุมที่วางตัวเลขก็อาจแค่ใช้เมธอด set_rlabel_position โดยใส่ค่าตัวเลขเป็นหน่วยองศาลงไป เช่น
แบบนี้ก็จะย้ายไปอยู่มุมซ้ายล่าง
การปรับเส้นรอบวงให้ไปทำที่ออบเจ็กต์ในแอตทริบิวต์ของแกนซึ่งมีชื่อว่า spines['polar'] เราสามารถปรับอะไรต่างๆได้เช่นเดียวกับ spines['top'], spines['bottom'], spines['left'] และ spines['right'] ของระบบพิกัดฉาก แต่ในระบบพิกัดฉากมีแค่ spines['polar'] อันเดียวให้ปรับ
การปรับ แต่งทำได้คล้่ายกัน เช่น แต่งสีโดย set_color ปรับความกว้างด้วย set_lw ปรับรูปแบบเส้นด้วย set_ls หรือทำให้หายไปด้วย set_visible(0)
ส่วนการปรับขอบเขตการแสดงผลนั้นระบบพิกัดเชิงขั้วจะไม่มีอิสระเท่ากับพิกัดฉาก เพราะยังไงมุมก็ไล่จาก 0 ถึง 360 สิ่งที่ปรับได้มีเพียง r ต่ำสุดและสูงสุดเท่านั้น
การปรับ r สูงสุดทำได้โดยใช้เมธอด set_ylim หรือฟังก์ชัน plt.ylim เช่น
plt.ylim หรือ set_ylim นี้อาจเขียนแทนด้วยเมธอด set_rlim ก็ได้ นอกจากนี้ยังอาจใช้เมธอด set_rmax และ set_rmin เพื่อกำหนดขอบเขตได้ด้วย
เวลาที่ใช้ระบบพิกัดฉากถ้าไม่ได้ตั้งอะไรจะมีเส้นกริดขึ้นมาโดยอัตโนมัติ เราสามารถลบเส้นกริดได้โดยใช้เมธอด grid ใส่ค่า 0 ให้
หรือหากต้องการปรับเส้นกริดให้เป็นไปตามที่ต้องการก็ทำได้ในลักษณะเดียวกับพิกัดฉาก เช่น
นอกจากนี้ก็ยังสามารถใช้ฟังก์ชัน plt.tick_params หรือเมธอด tick_params เพื่อปรับคุณสมบัติต่างๆของตัวเลขขีดบอก เช่นสีและขนาด
วาดกราฟและแผนภาพชนิดอื่นๆ
เช่นเดียวกับกราฟเส้น แผนภาพอื่นๆอีกหลายชนิดก็สามารถวาดในระบบพิกัดเชิงขั้วได้ ตัวอย่าง
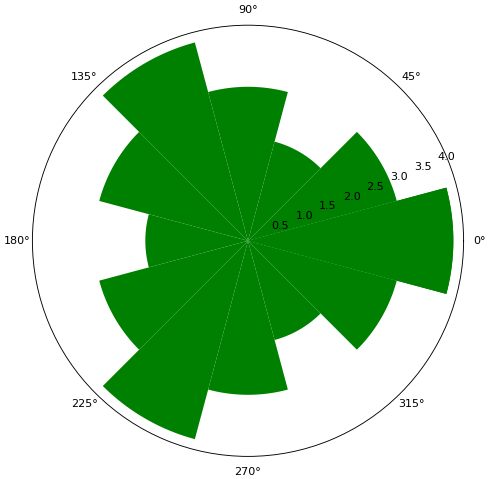
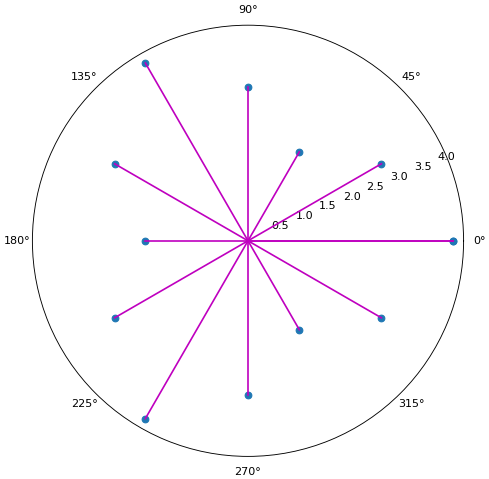
ตัวอย่างแผนภูมิแท่งและกราฟไม้ขีดไฟ
กราฟระบายสีระหว่างช่วง

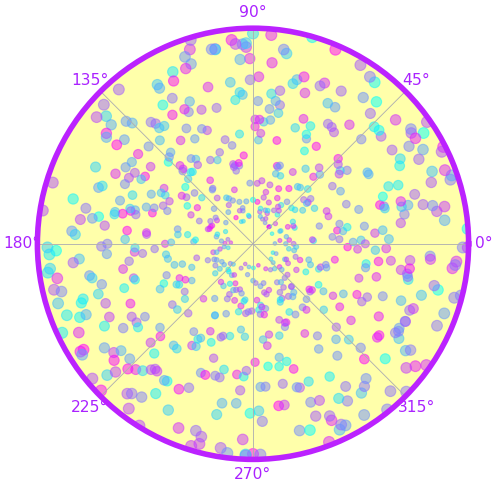
แผนภาพการกระจาย
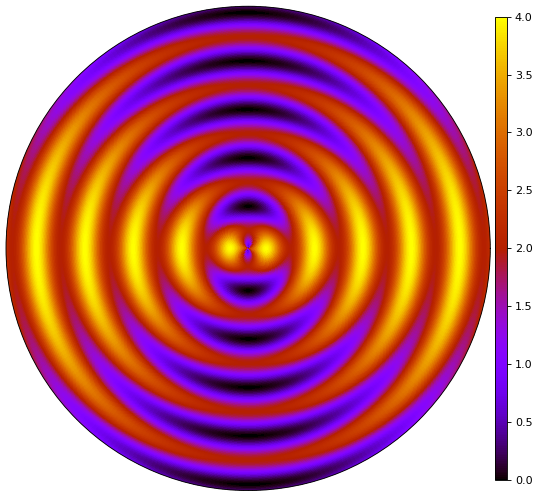
แผนภาพไล่สี
คอนทัวร์
เส้นกระแส
อ้างอิง
แต่หากต้องการทำให้ทุกอย่างอยู่ในระบบพิกัดเชิงขั้ว matplotlib ก็สามารถทำได้เช่นกัน
วาดกราฟในพิกัดเชิงขั้ว
การเขียนให้อยู่ในรูปพิกัดเชิงขั้วทำได้โดยกำหนดที่ตัว axes โดยตอนสร้าง axes ขึ้นมาให้ใส่คีย์เวิร์ดว่า polar=1 หรือไม่ก็ projection='polar'
จากนั้นเวลาวาดกราฟก็ใช้คำสั่งวาดแบบเดียวกับที่ใช้กันมาในระบบพิกัดฉาก แต่ค่าที่ต้องใส่จะใช้อาร์กิวเมนต์ตัวแรกเป็นค่ามุม และตัวหลังเป็นระยะห่างจากใจกลาง
ค่ามุมมีหน่วยเป็นเรเดียน ดังนั้นหากจะใส่หน่วยเป็นองศาก็ต้องแปลงก่อน โดยอาจใช้ฟังก์ชัน np.radians ช่วย
ตัวอย่าง วาดกราฟซึ่งมีระยะห่างจากใจกลางเพิ่มตามมุม
import numpy as np
import matplotlib.pyplot as plt
mum = np.linspace(0,360,361)
r = mum
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.plot(np.radians(mum),r)
plt.show()
import matplotlib.pyplot as plt
mum = np.linspace(0,360,361)
r = mum
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.plot(np.radians(mum),r)
plt.show()
แค่นี้ก็ออกมาเป็นพิกัดเชิงขั้วอย่างง่ายแล้ว

ตรงนี้หากเราตัดบรรทัด plt.axes(polar=1) ออกไปแล้วลองวาดใหม่ผลที่ได้ก็จะได้เป็นกราฟเส้นตรงธรรมดา

โดยในที่นี้แกนนอนคือมุม แกนตั้งคือระยะห่างจากใจกลาง จะเห็นว่าดูแล้วก็เหมือนกับว่าพิกัดเชิงขั้วคือการเอากราฟนี้ไปวาดใหมโดย เปลี่ยนแกนนอนเป็นค่ามุมและแกนตั้งเป็นระยะห่างจากใจกลางนั่นเอง
พิกัดเชิงขั้วถ้าหากวนครบ 360 องศาก็จะกลับมาอยู่ที่มุมเดิม ดังนั้นจะเห็นกราฟที่วนซ้อนกันไปเรื่อยๆได้ กราฟ cos ธรรมดาในระบบพิกัดฉากพอมาอยู่ในระบบพิกัดเชิงขั้วก็กลายเป็นลวดลายสวยงามแบบ นี้ได้
mum = np.linspace(0,3600,3601)
r = 1+np.cos(np.radians(mum*1.1))
plt.figure(figsize=[9,6])
plt.subplot(121)
plt.plot(np.radians(mum),r)
plt.subplot(122,polar=1)
plt.plot(np.radians(mum),r)
plt.subplots_adjust(0.05,0.05,0.97,0.97,0.1,0.1)
plt.show()
r = 1+np.cos(np.radians(mum*1.1))
plt.figure(figsize=[9,6])
plt.subplot(121)
plt.plot(np.radians(mum),r)
plt.subplot(122,polar=1)
plt.plot(np.radians(mum),r)
plt.subplots_adjust(0.05,0.05,0.97,0.97,0.1,0.1)
plt.show()

ที่จริงแล้วหากไม่ต้องการวาดให้อยู่ในรูปพิกัดเชิงขั้วเราอาจจะแปลงจาก r,θ เป็น x,y เองก็ได้ด้วยการคำนวณโดย x = rcosθ, y = rsinθ
ลองทำการคำนวณแปลงเป็น x,y แล้วพล็อตกราฟธรรมดาก็จะได้กราฟแบบเดียวกัน เพียงแต่อยู่ในระบบพิกัดฉาก
mum = np.linspace(0,3600,3601)
plt.figure(figsize=[7,7])
r = 1+np.cos(np.radians(mum*1.1))
x = r*np.cos(np.radians(mum))
y = r*np.sin(np.radians(mum))
plt.plot(x,y)
plt.show()
plt.figure(figsize=[7,7])
r = 1+np.cos(np.radians(mum*1.1))
x = r*np.cos(np.radians(mum))
y = r*np.sin(np.radians(mum))
plt.plot(x,y)
plt.show()

การปรับแต่ง
โดยหลักแล้วกราฟในพิกัดเชิงขั้วก็สามารถปรับแต่งอะไรต่างๆได้ในลักษณะคล้ายกับของพิกัดฉาก แต่ก็มีความแตกต่างออกไปบ้างเล็กน้อย
ลองดูตัวอย่างเช่นการแก้ตำแหน่งขีดบอกค่านั้นทำได้โดยใช้ฟังก์ชัน plt.xticks กับ plr.yticks หรือด้วยเมธอด set_xticks กับ set_yticks ได้เหมือนกัน โดย xticks ในที่นี้จะเป็นขีดของมุม ส่วน yticks เป็นขีดของระยะห่างจากใจกลาง
mum = np.linspace(0,7200,3601)
r = 1+np.cos(np.radians(mum*1.05))
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFDDCC')
plt.xticks(np.radians(np.arange(0,360,30))) # ตั้งให้แสดงทุก 30 องศา
plt.yticks([]) # ใส่ลิสต์ว่างแล้วตัวเลขแนวรัศมีจะหายไป
ax.plot(np.radians(mum),r,'r')
plt.show()
r = 1+np.cos(np.radians(mum*1.05))
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFDDCC')
plt.xticks(np.radians(np.arange(0,360,30))) # ตั้งให้แสดงทุก 30 องศา
plt.yticks([]) # ใส่ลิสต์ว่างแล้วตัวเลขแนวรัศมีจะหายไป
ax.plot(np.radians(mum),r,'r')
plt.show()

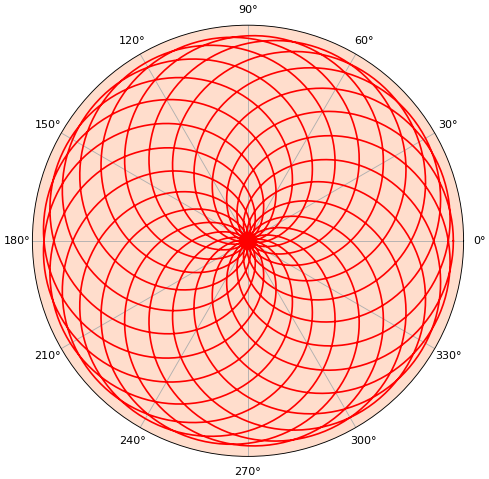
จะเห็นว่าค่า xticks ที่ป้อนเข้าไปนั้นต้องเป็นหน่วยเรเดียน แต่พอแสดงผลออกมาจริงๆกลับถูกเปลี่ยนให้เป็นหน่วยองศาโดยอัตโนมัติ
การเปลี่ยนการแสดงผลให้เป็นหน่วยเรเดียนหรือเป็นอะไรอื่นๆอาจทำได้โดยใช้ set_xticklabels
ลองพิมพ์เพิ่มลงไปตามนี้จะได้ค่าเป็นหน่วยเรเดียน
ax.set_xticklabels(np.radians(np.arange(0,360,30)))
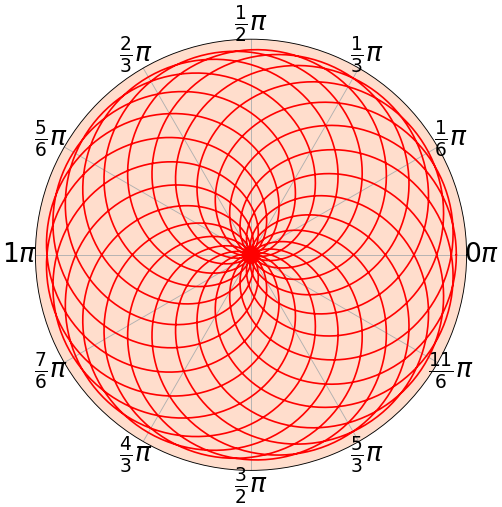
หรือลองใช้ latex เพื่อให้ดูสวยขึ้น เช่น พิมพ์ตามนี้เพิ่มเข้าไป
xtl = []
for x in np.arange(12):
if(x%6==0):
xtl += [r'$%d\pi$'%(x/6)]
elif(x%3==0):
xtl += [r'$\frac{%d}{2}\pi$'%(x/3)]
elif(x%2==0):
xtl += [r'$\frac{%d}{3}\pi$'%(x/2)]
else:
xtl += [r'$\frac{%d}{6}\pi$'%x]
ax.set_xticklabels(xtl,fontsize=24)
for x in np.arange(12):
if(x%6==0):
xtl += [r'$%d\pi$'%(x/6)]
elif(x%3==0):
xtl += [r'$\frac{%d}{2}\pi$'%(x/3)]
elif(x%2==0):
xtl += [r'$\frac{%d}{3}\pi$'%(x/2)]
else:
xtl += [r'$\frac{%d}{6}\pi$'%x]
ax.set_xticklabels(xtl,fontsize=24)

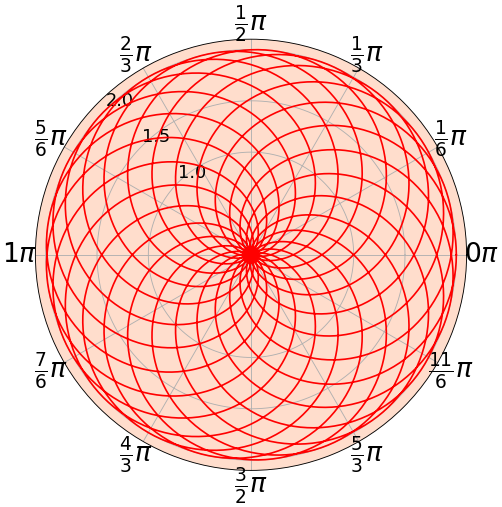
สำหรับค่าขีดบอกตำแหน่งในแนวรัศมีนั้นนอกจากจะปรับได้ด้วย set_yticks แล้วยังอาจใช้ set_rgrids ซึ่งจะดีกว่าตรงที่สามารถตั้งตำแหน่งที่จะวางได้ด้วย โดยใส่คีย์เวิร์ด angle หน่วยเป็นองศา
ax.set_rgrids([1,1.5,2],angle=135,fontsize=16)

นอกจากนี้หากต้องการปรับแค่ตำแหน่งมุมที่วางตัวเลขก็อาจแค่ใช้เมธอด set_rlabel_position โดยใส่ค่าตัวเลขเป็นหน่วยองศาลงไป เช่น
ax.set_rlabel_position(225)
แบบนี้ก็จะย้ายไปอยู่มุมซ้ายล่าง
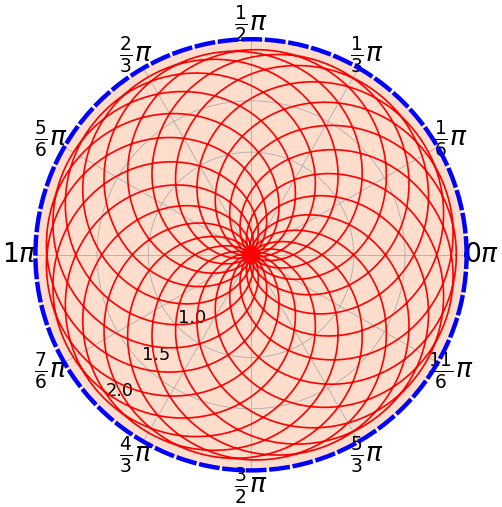
การปรับเส้นรอบวงให้ไปทำที่ออบเจ็กต์ในแอตทริบิวต์ของแกนซึ่งมีชื่อว่า spines['polar'] เราสามารถปรับอะไรต่างๆได้เช่นเดียวกับ spines['top'], spines['bottom'], spines['left'] และ spines['right'] ของระบบพิกัดฉาก แต่ในระบบพิกัดฉากมีแค่ spines['polar'] อันเดียวให้ปรับ
การปรับ แต่งทำได้คล้่ายกัน เช่น แต่งสีโดย set_color ปรับความกว้างด้วย set_lw ปรับรูปแบบเส้นด้วย set_ls หรือทำให้หายไปด้วย set_visible(0)
ax.spines['polar'].set_color('b')
ax.spines['polar'].set_lw(4)
ax.spines['polar'].set_ls('--')
ax.spines['polar'].set_lw(4)
ax.spines['polar'].set_ls('--')

ส่วนการปรับขอบเขตการแสดงผลนั้นระบบพิกัดเชิงขั้วจะไม่มีอิสระเท่ากับพิกัดฉาก เพราะยังไงมุมก็ไล่จาก 0 ถึง 360 สิ่งที่ปรับได้มีเพียง r ต่ำสุดและสูงสุดเท่านั้น
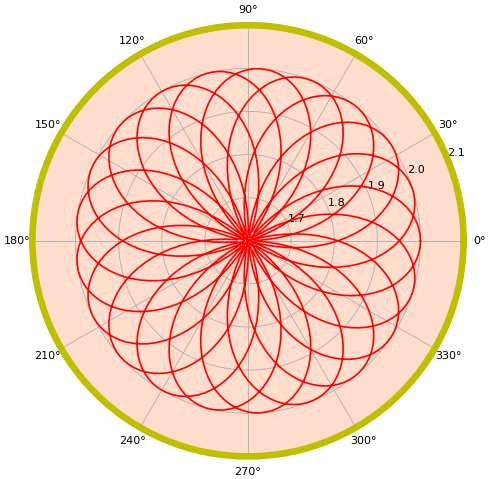
การปรับ r สูงสุดทำได้โดยใช้เมธอด set_ylim หรือฟังก์ชัน plt.ylim เช่น
mum = np.linspace(0,7200,3601)
r = 1+np.cos(np.radians(mum*1.05))
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFDDCC')
ax.set_xticks(np.radians(np.arange(0,360,30)))
ax.spines['polar'].set_color('y')
ax.spines['polar'].set_lw(6)
plt.ylim([1.6,2.1]) # หรือ ax.set_ylim([1.6,2.1])
ax.plot(np.radians(mum),r,'r')
plt.show()
r = 1+np.cos(np.radians(mum*1.05))
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFDDCC')
ax.set_xticks(np.radians(np.arange(0,360,30)))
ax.spines['polar'].set_color('y')
ax.spines['polar'].set_lw(6)
plt.ylim([1.6,2.1]) # หรือ ax.set_ylim([1.6,2.1])
ax.plot(np.radians(mum),r,'r')
plt.show()

plt.ylim หรือ set_ylim นี้อาจเขียนแทนด้วยเมธอด set_rlim ก็ได้ นอกจากนี้ยังอาจใช้เมธอด set_rmax และ set_rmin เพื่อกำหนดขอบเขตได้ด้วย
ax.set_rmin(0)
ax.set_rmax(0.4)
ax.set_rmax(0.4)
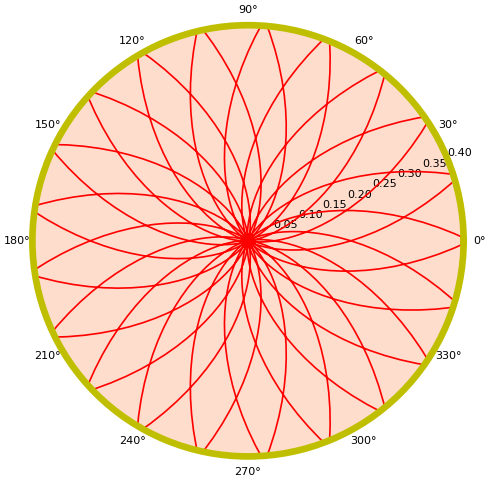
เวลาที่ใช้ระบบพิกัดฉากถ้าไม่ได้ตั้งอะไรจะมีเส้นกริดขึ้นมาโดยอัตโนมัติ เราสามารถลบเส้นกริดได้โดยใช้เมธอด grid ใส่ค่า 0 ให้
ax.grid(0)

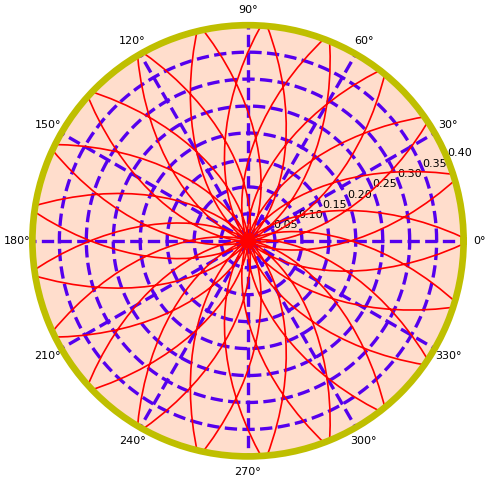
หรือหากต้องการปรับเส้นกริดให้เป็นไปตามที่ต้องการก็ทำได้ในลักษณะเดียวกับพิกัดฉาก เช่น
ax.grid(c='#5500EE', ls='--', lw=3)

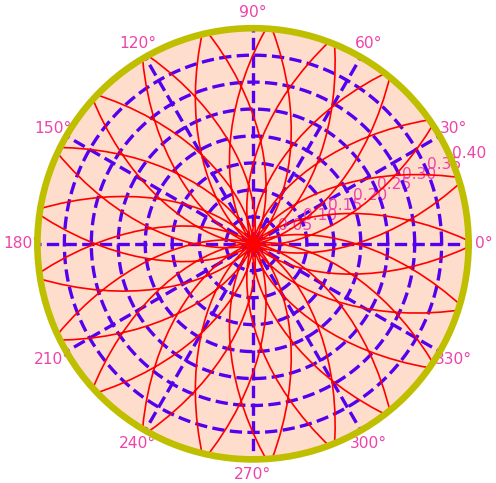
นอกจากนี้ก็ยังสามารถใช้ฟังก์ชัน plt.tick_params หรือเมธอด tick_params เพื่อปรับคุณสมบัติต่างๆของตัวเลขขีดบอก เช่นสีและขนาด
ax.tick_params(colors='#EE44AA',labelsize=14)

วาดกราฟและแผนภาพชนิดอื่นๆ
เช่นเดียวกับกราฟเส้น แผนภาพอื่นๆอีกหลายชนิดก็สามารถวาดในระบบพิกัดเชิงขั้วได้ ตัวอย่าง
ตัวอย่างแผนภูมิแท่งและกราฟไม้ขีดไฟ
mum = np.linspace(0,360,13)
r = 3+np.cos(np.radians(mum*3))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.bar(np.radians(mum),r,color='g',width=np.radians(30))
plt.grid(0)
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.stem(np.radians(mum),r,'m')
plt.grid(0)
plt.show()
r = 3+np.cos(np.radians(mum*3))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.bar(np.radians(mum),r,color='g',width=np.radians(30))
plt.grid(0)
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.stem(np.radians(mum),r,'m')
plt.grid(0)
plt.show()


กราฟระบายสีระหว่างช่วง
mum = np.linspace(0,360,3601)
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.yticks([]) # ลบเลขบอกค่าตามแนวรัศมี
r = [0]*5
for i in range(5):
r[i] = 2+i*2+np.cos(np.radians(mum*(5*2**i)))
cmap = plt.get_cmap('summer_r')
fc = cmap(i/4.)
if(i==0):
plt.fill_between(np.radians(mum),r[i],facecolor=fc,lw=0)
else:
plt.fill_between(np.radians(mum),r[i],r[i-1],facecolor=fc,lw=0)
plt.show()
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.yticks([]) # ลบเลขบอกค่าตามแนวรัศมี
r = [0]*5
for i in range(5):
r[i] = 2+i*2+np.cos(np.radians(mum*(5*2**i)))
cmap = plt.get_cmap('summer_r')
fc = cmap(i/4.)
if(i==0):
plt.fill_between(np.radians(mum),r[i],facecolor=fc,lw=0)
else:
plt.fill_between(np.radians(mum),r[i],r[i-1],facecolor=fc,lw=0)
plt.show()

แผนภาพการกระจาย
mum = np.linspace(0,720,721)
r = np.random.uniform(1,10,721)
c = np.random.uniform(0,1,721)
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFFFAA')
ax.set_yticks([])
ax.set_ylim([0,10])
ax.scatter(np.radians(mum),r,c=c,s=r*10,cmap='cool',alpha=0.5)
ax.spines['polar'].set_color('#BB22FF')
ax.spines['polar'].set_lw(5)
ax.tick_params(colors='#AA22FF',labelsize=14)
plt.show()
r = np.random.uniform(1,10,721)
c = np.random.uniform(0,1,721)
plt.figure(figsize=[7,7])
ax = plt.axes(polar=1,facecolor='#FFFFAA')
ax.set_yticks([])
ax.set_ylim([0,10])
ax.scatter(np.radians(mum),r,c=c,s=r*10,cmap='cool',alpha=0.5)
ax.spines['polar'].set_color('#BB22FF')
ax.spines['polar'].set_lw(5)
ax.tick_params(colors='#AA22FF',labelsize=14)
plt.show()

แผนภาพไล่สี
mum,r = np.meshgrid(np.linspace(0,360,361),np.linspace(0,1,401))
c = 2+np.cos(np.radians(mum*2))+np.sin(np.radians(r*1800-45))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.xticks([])
plt.yticks([])
plt.pcolormesh(np.radians(mum),r,c,cmap='gnuplot')
plt.colorbar(pad=0.01,aspect=40,fraction=0.05,shrink=0.9)
plt.subplots_adjust(0.05,0.05,0.97,0.97,0.1,0.1)
plt.show()
c = 2+np.cos(np.radians(mum*2))+np.sin(np.radians(r*1800-45))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.xticks([])
plt.yticks([])
plt.pcolormesh(np.radians(mum),r,c,cmap='gnuplot')
plt.colorbar(pad=0.01,aspect=40,fraction=0.05,shrink=0.9)
plt.subplots_adjust(0.05,0.05,0.97,0.97,0.1,0.1)
plt.show()

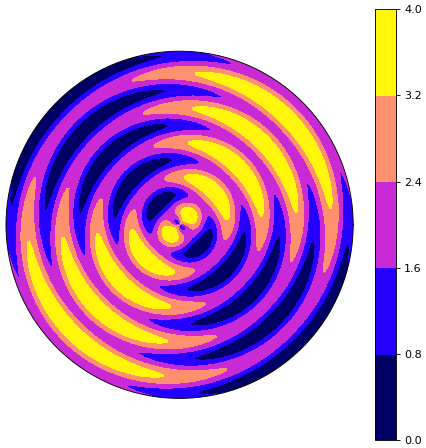
คอนทัวร์
mum,r = np.meshgrid(np.linspace(0,360,91),np.linspace(0,1,101))
c = 2+np.sin(np.radians(mum*2))+np.sin(np.radians(r*1800-45))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.xticks([])
plt.yticks([])
plt.contourf(np.radians(mum),r,c,5,cmap='gnuplot2')
plt.colorbar()
plt.show()
c = 2+np.sin(np.radians(mum*2))+np.sin(np.radians(r*1800-45))
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.xticks([])
plt.yticks([])
plt.contourf(np.radians(mum),r,c,5,cmap='gnuplot2')
plt.colorbar()
plt.show()

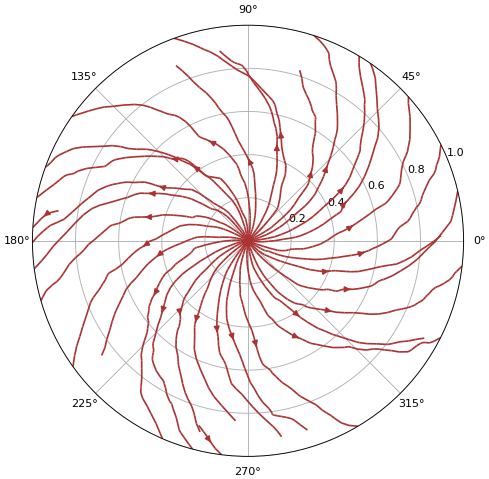
เส้นกระแส
mum,r = np.meshgrid(np.linspace(0,3600,1801),np.linspace(0,1,101))
u = r*0.1+np.random.rand(101,1801)
v = np.random.rand(101,1801)
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.ylim([0,1])
plt.streamplot(np.radians(mum),r,u,v,color='#AA3333')
plt.show()
u = r*0.1+np.random.rand(101,1801)
v = np.random.rand(101,1801)
plt.figure(figsize=[7,7])
plt.axes(polar=1)
plt.ylim([0,1])
plt.streamplot(np.radians(mum),r,u,v,color='#AA3333')
plt.show()

อ้างอิง
http://cordea.hatenadiary.com/entry/2014/09/23/181602
http://d.hatena.ne.jp/teruaki_enoto/20101109/1289337962
http://python.dogrow.net/?p=269
http://d.hatena.ne.jp/teruaki_enoto/20101109/1289337962
http://python.dogrow.net/?p=269