ต่อจาก บทที่ ๑๙

ในบทนี้จะพูดถึงการแจกแจงสติวเดนต์ที (学生t-分布, Student's t-distribution) ซึ่งเป็นการแจกแจงที่เกิดขึ้นเมื่อต้องการหาการแจกแจงความน่าจะเป็นของค่าที่แจกแจงแบบปกติโดยมีค่าส่วนเบี่ยงเบนมาตรฐาน σ หรือพารามิเตอร์ความเที่ยงตรง α=1/σ² ไม่แน่นอน




การการแจกแจงแบบปกติที่ σ มีความไม่แน่นอน

จากตรงนี้จะทำการจัดรูปสมการในลักษณะที่คล้ายกับบทที่แล้ว แค่คราวนี้พารามิเตอร์ที่มีความไม่แน่นอนคือส่วนเบี่ยงเบนมาตรฐาน σ ซึ่งเพื่อความสะดวกในที่นี้จะเขียนในรูปของพารามิเตอร์ความเที่ยงตรง α=1/σ²

เริ่มพิจารณาจากทฤษฎีบทของเกาส์ เช่นเดียวกับสมการ 19.6 แต่คราวนี้พารามิเตอร์เป็น α



เอาส่วนที่ไม่เกี่ยวข้องกับ x มารวมไว้ในค่าคงที่เช่นเคย

ค่าตัวแปร x แจกแจงความน่าจะเป็นแบบปกติเป็น


การแจกแจงความน่าจะเป็นของพารามิเตอร์ก็คือการแจกแจงความน่าจะเป็นภายหลัง ยกมาจากบทที่ ๑๖ ได้เป็น



แทนสมการ 20.2 และ 20.3 ลงในสมการ 20.1 จะได้



ผลที่ได้นี้ออกมาเป็นรูปของการแจกแจงแบบใหม่ซึ่งก็คือการแจกแจงสติวเดนต์ทีดังที่ได้กล่าวไว้ข้างต้นนั่นเอง




การแจกแจงสติวเดนต์ที

การแจกแจงสติวเดนต์ทีมีรูปทั่วไปเป็น


พารามิเตอร์ของการแจกแจงนี้คือ ν ซึ่งถูกเรียกว่าเป็นองศาเสรี (自由度, degree of freedom)

กราฟแสดงการแจกแจงเปรียบเทียบกรณีต่างๆ



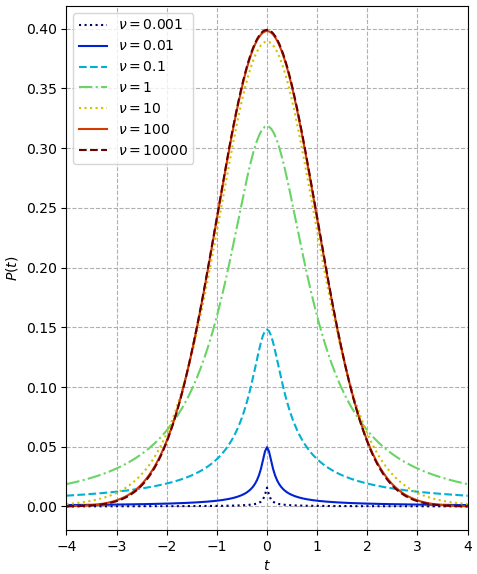
ลักษณะกราฟจะเป็นลักษณะสมมาตรที่มีใจกลางที่ 0 ค่า ν ยิ่งสูงจุดสูงสุด เมื่อค่าสูง ν ขึ้นจนเข้าใกล้อนันต์ก็จะกลายเป็นเทียบเท่ากับการแจกแจงแบบปกติไป

การแจกแจงสติวเดนต์ทีมีลักษณะสมมาตรเช่นเดียวกับการแจกแจงแบบปกติ ทั้งค่าคาดหมายและจุดกึ่งกลาง (ฐานนิยม) ล้วนอยู่ที่ตำแหน่ง 0 เช่นเดียวกับการแจกแจงปกติมาตรฐาน

ส่วนความแปรปรวนจะเป็น


ซึ่งถ้าค่ามากจนใกล้อนันต์ ความแปรปรวนก็จะเป็น 1 เช่นเดียวกับการแจกแจงแบบปกติมาตรฐาน

สมการ 20.4 จะได้ออกมาเป็นสมการ 20.5 หากเทียบแทนค่าตามนี้


โดยค่าคงที่คือ


แล้วจะได้ว่าการแจกแจงความน่าจะเป็นของ x เป็น


วาดกราฟแสดงการแจกแจงเปรียบเทียบกรณีที่ ν₀ และ β₀ เป็นค่าต่างๆ โดยให้ μ=5



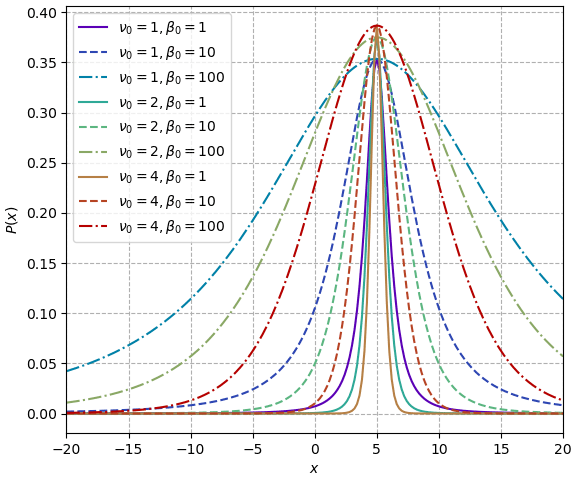
ในที่นี้ β₀ เป็นตัวปรับสัดส่วน ยิ่งค่ามากกราฟก็ยิ่งกว้าง ส่วน μ คือตำแหน่งในกลางของการแจกแจง




ความสัมพันธ์ระหว่างการแจกแจงสติวเดนต์ทีกับการแจกแจงไคกำลังสอง

ถ้า y เป็นตัวแปรสุ่มที่มีความน่าจะเป็นเป็นการแจกแจงแบบปกติมาตรฐาน และ z เป็นตัวแปรสุ่มที่มีความน่าจะเป็นเป็นการแจกแจงไคกำลังสองซึ่งมีองศาเสรีเป็น k แล้ว ค่า


จะมีความน่าจะเป็นเป็นการแจกแจงแบบสติวเดนต์ทีซึ่งมีองศาเสรีเป็น k เช่นกัน


ตัวอย่างการลองสุ่ม 10000 ตัวแล้วทำฮิสโทแกรม เมื่อให้ k=2 ภาพบนคือการแจกแจงปกติ ภาพกลางคือการแจกแจงไคกำลังสอง และภาพล่างสุดคือการแจกแจงที่ได้จากผลของสองการแจกแจงด้านบน ซึ่งจะเป็นการแจกแจงสติวเดนต์ที ส่วนเส้นกราฟแสดงฟังก์ชันการแจกแจงความหนาแน่นจริงๆ



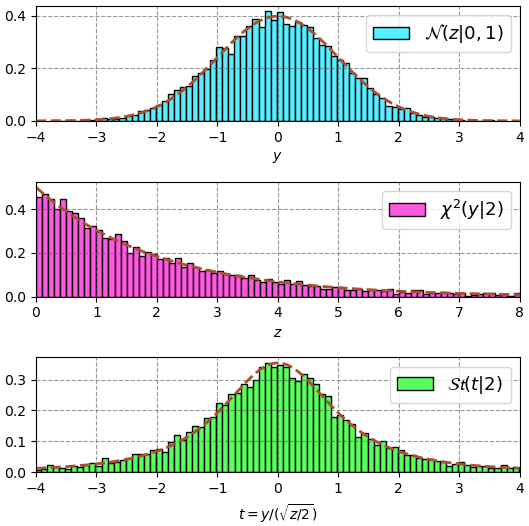
ลองทำเหมือนเดิมแต่ให้ k=3





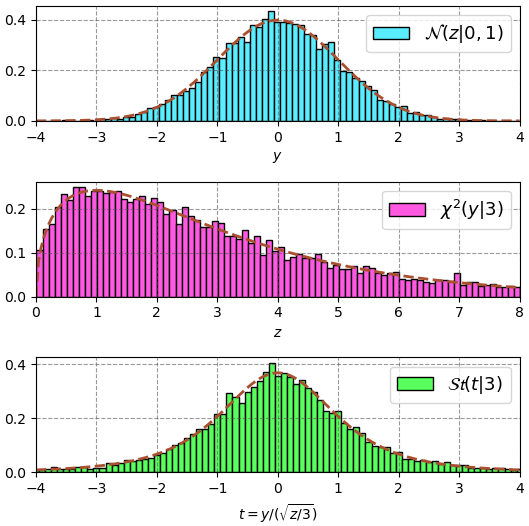
บทถัดไป >> บทที่ ๒๑

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文