การวิเคราะห์องค์ประกอบหลักด้วย sklearn
เขียนเมื่อ 2019/09/21 21:32
แก้ไขล่าสุด 2022/07/11 12:35
หลังจากที่ได้อธิบายหลักการของการวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis) หรือ PCA ไปแล้วใน https://phyblas.hinaboshi.com/20180727
และพูดถึงวิธีการคำนวณหาองค์ประกอบอย่างรวดเร็วโดยการแยกค่าเอกฐาน (奇异值分解, singular value decomposition) หรือ SVD https://phyblas.hinaboshi.com/20190916
คราวนี้จะมาใช้ sklearn ในการวิเคราะห์องค์ประกอบหลัก
sklearn มีฟังก์ชันที่ใช้ทำการวิเคราะห์องค์ประกอบหลัก คือ sklearn.decomposition.PCA
การคำนวณเพื่อหาองค์ประกอบภายในฟังก์ชันนี้ใช้ SVD ซึ่งคำนวณได้ค่อนข้างเร็วแม้จำนวนมิติของข้อมูลจะมาก
และปกติเวลาทำการวิเคราะห์องค์ประกอบหลักจะต้องทำให้ค่าเฉลี่ยของข้อมูลเป็น 0 ในทุกมิติก่อน แต่หากใช้ sklearn จุดกึ่งกลางจะถูกหาให้โดยอัตโนมัติ
ต่อไปจะเป็นคำอธิบายและยกตัวอย่างวิธีการใช้
ในบทความนี้จะไม่อธิบายหลักการของการวิเคราะห์องค์ประกอบหลัก เพราะได้เขียนไปแล้วในบทความข้างต้น บทความนี้จะเน้นที่การคำนวณโดยใช้ sklearn
ตัวอย่าง สร้างข้อมูล ๓ มิติแล้ววิเคราะห์องค์ประกอบหลัก เอาองค์ประกอบหลักมา ๒ มิติ
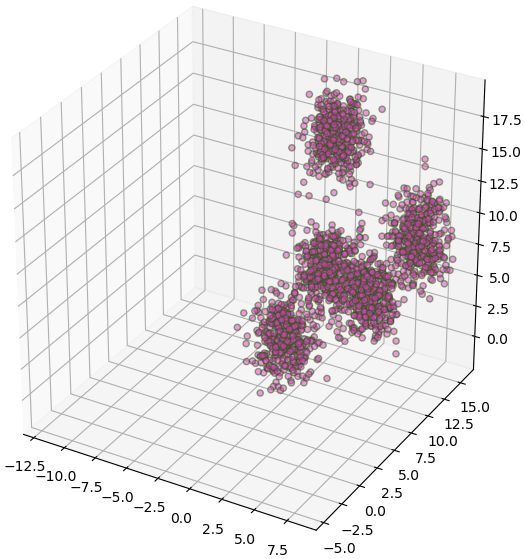
วิธีการใช้นั้นจะเริ่มจากสร้างออบเจ็กต์ของคลาส sklearn.decomposition.PCA โดยหากต้องการลดจำนวนมิติก็ให้กำหนดค่าจำนวนองค์ประกอบลงไปด้วย
จากนั้นก็ใช้เมธอด fit โดยใส่ข้อมูลที่ต้องการจะวิเคราะห์เข้าไป
สุดท้ายใช้เมธอด transform เพื่อแปลงข้อมูลให้อยู่ในระบบพิกัดขององค์ประกอบที่ได้มา
ในตัวอย่างนี้ X คือข้อมูลเดิม มี ๓ มิติ นำไปวิเคราะห์องค์ประกอบหลักด้วย fit แล้วใช้ transform เพื่อเป็น Xi ซึ่งเป็นข้อมูลในพิกัดองค์ประกอบ ซึ่งเหลือ ๒ มิติ
เมื่อสั่ง fit ไป ค่าที่ป้อนลงไปจะถูกใช้ในการคำนวณ SVD แล้วผลที่ได้จากการคำนวณต่างๆเก็บเอาไว้ในแอตทริบิวต์ต่างๆภายในออบเจ็กต์ซึ่งลงท้ายด้วย _ ซึ่งสามารถนำมาใช้ได้ ดังนี้
ลองดูค่าแต่ละตัวนี้
ได้
ทั้ง explained_variance_ หรือ explained_variance_ratio_ และ singular_values_ ล้วนเป็นอาเรย์จำนวนเท่ากับจำนวนองค์ประกอบที่เลือกเหลือไว้ บอกถึงความสำคัญขององค์ประกอบแต่ละตัว เรียงตามลำดับมากที่สุด
โดยที่ explained_variance_ratio_ เหมือนกับ explained_variance_ แค่ทำให้ผลรวมเหลือเป็น 1
ลองเทียบระหว่าง ๒ ค่านี้ดู
ผลรวมของ explained_variance_ratio_ จะเป็นตัวบอกว่ามิติที่เหลืออยู่นั้นรักษาข้อมูลเดิมไว้ได้ดีแค่ไหน
ค่าเข้าใกล้ 1 หมายความว่ามิติที่ตัดทิ้งไปนั้นไม่ได้สำคัญ แต่ถ้ายิ่งเลขน้อยแสดงว่าข้อมูลอยู่ในมิติที่ตัดทิ้งไปมาก พอตัดมิติไปข้อมูลจะเปลี่ยนไปจากเดิมมาก
ค่าผลรวมจะเป็น 1 ถ้าหากจำนวนมิติขององค์ประกอบเท่ากับข้อมูลก่อนแปลง
singular_values_ นั้นถ้ายกกำลังสองจะพบว่าอัตราส่วนของแต่ละค่าจะเท่ากับ explained_variance_
ส่วน components_ คืออาเรย์ที่บอกค่าน้ำหนักขององค์ประกอบแต่ละตัวภายในข้อมูลเดิม
ขนาดเป็น จำนวนองค์ประกอบที่กำหนด × จำนวนมิติเดิม
ค่าที่ได้มาในพิกัดใหม่จะมีค่าเฉลี่ยในทุกองค์ประกอบเป็น 0 เสมอ ไม่ว่าข้อมูลเดิมจะมีค่าเฉลี่ยในแต่ละมิติอยู่ตรงไหน
ที่ว่า sklearn จะทำการหาค่าเฉลี่ยของข้อมูลให้อัตโนมัติก่อนที่จะทำการคำนวณนั้น ค่าเฉลี่ยนั้นเก็บอยู่ที่ mean_ นั่นเอง ตอนที่แปลงกลับค่านี้ก็ถูกนำมาใช้
เมธอด fit นั้นการคำนวณภายในก็คือการเอาข้อมูลที่ใส่ไปมาลบค่าเฉลี่ยแล้ว
ในทางกลับกันสามารถแปลงข้อมูลกลับจากพิกัดขององค์ประกอบกลับเป็นข้อมูลในพิกัดเดิมได้โดยคูณ components_ แล้วก็บวกด้วย mean_ หรือใช้เมธอด .inverse_transform()
ลองทำการแปลงข้อมูลกลับ
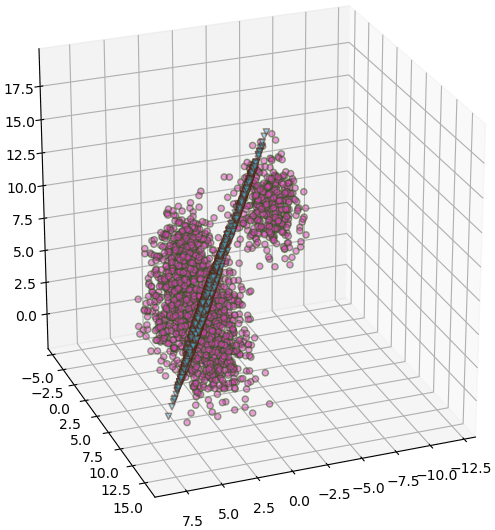
จะเห็นว่าค่าแปลงกลับที่ได้นี้เมื่อมาวาดในระบบพิกัดเดิมซึ่งเป็น ๓ มิติจะได้เป็นระนาบ เพราะเดิมทีเป็นข้อมูลที่ถูกลดรูปเหลือ ๒ มิติโดยทิ้งมิติที่สำคัญน้อยที่สุดไป
หากข้อมูลที่จะวิเคราะห์และแปลงเป็นตัวเดียวกันดังเช่นในตัวอย่างนี้สามารถใช้เมธอด fit_transform แทนที่จะใช้ fit แล้วค่อย transform อีกที
ลองสร้างข้อมูลใหม่คล้ายเดิม แต่แค่คราวนี้เปลี่ยนมาใช้ fit_transform แทน
และพูดถึงวิธีการคำนวณหาองค์ประกอบอย่างรวดเร็วโดยการแยกค่าเอกฐาน (奇异值分解, singular value decomposition) หรือ SVD https://phyblas.hinaboshi.com/20190916
คราวนี้จะมาใช้ sklearn ในการวิเคราะห์องค์ประกอบหลัก
sklearn มีฟังก์ชันที่ใช้ทำการวิเคราะห์องค์ประกอบหลัก คือ sklearn.decomposition.PCA
การคำนวณเพื่อหาองค์ประกอบภายในฟังก์ชันนี้ใช้ SVD ซึ่งคำนวณได้ค่อนข้างเร็วแม้จำนวนมิติของข้อมูลจะมาก
และปกติเวลาทำการวิเคราะห์องค์ประกอบหลักจะต้องทำให้ค่าเฉลี่ยของข้อมูลเป็น 0 ในทุกมิติก่อน แต่หากใช้ sklearn จุดกึ่งกลางจะถูกหาให้โดยอัตโนมัติ
ต่อไปจะเป็นคำอธิบายและยกตัวอย่างวิธีการใช้
ในบทความนี้จะไม่อธิบายหลักการของการวิเคราะห์องค์ประกอบหลัก เพราะได้เขียนไปแล้วในบทความข้างต้น บทความนี้จะเน้นที่การคำนวณโดยใช้ sklearn
ตัวอย่าง สร้างข้อมูล ๓ มิติแล้ววิเคราะห์องค์ประกอบหลัก เอาองค์ประกอบหลักมา ๒ มิติ
from sklearn.decomposition import PCA
from sklearn import datasets
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(33)
# สร้างข้อมูล
X,_ = datasets.make_blobs(2000,n_features=3,centers=5,center_box=(0,14))
X[:,2] *= 1.6
# วาดภาพข้อมูล ๓ มิติก่อนแปลง
plt.figure(figsize=[6,6],dpi=100)
lim = {xyz+'lim': (X[:,i].max()-(X.max()-X.min()),X[:,i].max()) for i,xyz in enumerate('xyz')} # ขอบเขต
ax = plt.axes([0,0,1,1],projection='3d',**lim)
ax.scatter(*X.T,c='#dd44bb',edgecolor='#225511',alpha=0.5)
# สร้างออบเจ็กต์คลาส PCA เพื่อทำการวิเคราะห์องค์ประกอบ
pca = PCA(2) # กำหนดจำนวนมิติที่เหลือเป็น ๒
pca.fit(X) # ป้อนข้อมูลเพื่อให้ทำการวิเคราะห์
Xi = pca.transform(X) # แปลงข้อมูล
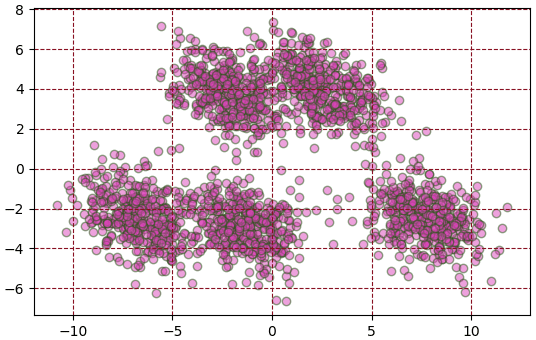
# วาดภาพข้อมูลหลังแปลง ซึ่งเป็น ๒ มิติ
plt.figure(dpi=100)
plt.axes(aspect=1)
plt.grid(ls='--',color='#881122')
plt.scatter(*Xi.T,c='#dd44bb',edgecolor='#225511',alpha=0.5)
plt.show()

วิธีการใช้นั้นจะเริ่มจากสร้างออบเจ็กต์ของคลาส sklearn.decomposition.PCA โดยหากต้องการลดจำนวนมิติก็ให้กำหนดค่าจำนวนองค์ประกอบลงไปด้วย
จากนั้นก็ใช้เมธอด fit โดยใส่ข้อมูลที่ต้องการจะวิเคราะห์เข้าไป
สุดท้ายใช้เมธอด transform เพื่อแปลงข้อมูลให้อยู่ในระบบพิกัดขององค์ประกอบที่ได้มา
ในตัวอย่างนี้ X คือข้อมูลเดิม มี ๓ มิติ นำไปวิเคราะห์องค์ประกอบหลักด้วย fit แล้วใช้ transform เพื่อเป็น Xi ซึ่งเป็นข้อมูลในพิกัดองค์ประกอบ ซึ่งเหลือ ๒ มิติ
เมื่อสั่ง fit ไป ค่าที่ป้อนลงไปจะถูกใช้ในการคำนวณ SVD แล้วผลที่ได้จากการคำนวณต่างๆเก็บเอาไว้ในแอตทริบิวต์ต่างๆภายในออบเจ็กต์ซึ่งลงท้ายด้วย _ ซึ่งสามารถนำมาใช้ได้ ดังนี้
| components_ | อาเรย์ค่าน้ำหนักขององค์ประกอบต่างๆ |
| explained_variance_ | ความบ่งบอกความแปรปรวน |
| explained_variance_ratio_ | อัตราความบ่งบอกความแปรปรวน |
| singular_values_ | ค่าเอกฐานที่คำนวณมาได้จาก SVD |
| mean_ | ค่าเฉลี่ยของข้อมูลเดิมในแต่ละมิติ |
| n_components_ | จำนวนองค์ประกอบหลัก |
| noise_variance_ | ค่าความแปรปรวนของคลื่นรบกวนภายในข้อมูล |
ลองดูค่าแต่ละตัวนี้
print('components_ =\n%s\n'%pca.components_)
print('explained_variance_ = %s\n'%pca.explained_variance_)
print('explained_variance_ratio_ = %s\n'%pca.explained_variance_ratio_)
print('singular_values_ = %s\n'%pca.singular_values_)
print('mean_ = %s\n'%pca.mean_)
print('n_components_ = %s\n'%pca.n_components_)
print('noise_variance_ = %s'%pca.noise_variance_)ได้
components_ =
[[-0.0036404 0.56933295 0.82209898]
[ 0.52655336 0.69999514 -0.48244001]]
explained_variance_ = [25.23336373 11.6322938 ]
explained_variance_ratio_ = [0.61504395 0.28352827]
singular_values_ = [224.59183887 152.48919736]
mean_ = [ 3.11679917 10.08830006 8.19599173]
n_components_ = 2
noise_variance_ = 4.161270420871972ทั้ง explained_variance_ หรือ explained_variance_ratio_ และ singular_values_ ล้วนเป็นอาเรย์จำนวนเท่ากับจำนวนองค์ประกอบที่เลือกเหลือไว้ บอกถึงความสำคัญขององค์ประกอบแต่ละตัว เรียงตามลำดับมากที่สุด
โดยที่ explained_variance_ratio_ เหมือนกับ explained_variance_ แค่ทำให้ผลรวมเหลือเป็น 1
ลองเทียบระหว่าง ๒ ค่านี้ดู
print(pca.explained_variance_/pca.explained_variance_ratio_) # ได้ [41.02692795 41.02692795]ผลรวมของ explained_variance_ratio_ จะเป็นตัวบอกว่ามิติที่เหลืออยู่นั้นรักษาข้อมูลเดิมไว้ได้ดีแค่ไหน
print(pca.explained_variance_ratio_.sum()) # ได้ 0.8985722151581703ค่าเข้าใกล้ 1 หมายความว่ามิติที่ตัดทิ้งไปนั้นไม่ได้สำคัญ แต่ถ้ายิ่งเลขน้อยแสดงว่าข้อมูลอยู่ในมิติที่ตัดทิ้งไปมาก พอตัดมิติไปข้อมูลจะเปลี่ยนไปจากเดิมมาก
ค่าผลรวมจะเป็น 1 ถ้าหากจำนวนมิติขององค์ประกอบเท่ากับข้อมูลก่อนแปลง
singular_values_ นั้นถ้ายกกำลังสองจะพบว่าอัตราส่วนของแต่ละค่าจะเท่ากับ explained_variance_
print(pca.explained_variance_/pca.singular_values_**2) # ได้ [0.00050025 0.00050025]ส่วน components_ คืออาเรย์ที่บอกค่าน้ำหนักขององค์ประกอบแต่ละตัวภายในข้อมูลเดิม
ขนาดเป็น จำนวนองค์ประกอบที่กำหนด × จำนวนมิติเดิม
ค่าที่ได้มาในพิกัดใหม่จะมีค่าเฉลี่ยในทุกองค์ประกอบเป็น 0 เสมอ ไม่ว่าข้อมูลเดิมจะมีค่าเฉลี่ยในแต่ละมิติอยู่ตรงไหน
ที่ว่า sklearn จะทำการหาค่าเฉลี่ยของข้อมูลให้อัตโนมัติก่อนที่จะทำการคำนวณนั้น ค่าเฉลี่ยนั้นเก็บอยู่ที่ mean_ นั่นเอง ตอนที่แปลงกลับค่านี้ก็ถูกนำมาใช้
เมธอด fit นั้นการคำนวณภายในก็คือการเอาข้อมูลที่ใส่ไปมาลบค่าเฉลี่ยแล้ว
(X-pca.mean_).dot(pca.components_.T) # เท่ากับ pca.transform(X)ในทางกลับกันสามารถแปลงข้อมูลกลับจากพิกัดขององค์ประกอบกลับเป็นข้อมูลในพิกัดเดิมได้โดยคูณ components_ แล้วก็บวกด้วย mean_ หรือใช้เมธอด .inverse_transform()
(Xi).dot(pca.components_)+pca.mean_ # เท่ากับ pca.inverse_transform(Xi)ลองทำการแปลงข้อมูลกลับ
plt.figure(figsize=[6,6],dpi=100)
ax = plt.axes([0,0,1,1],projection='3d',**lim)
ax.scatter(*X.T,c='#dd44bb',edgecolor='#225511',alpha=0.5)
X2 = pca.inverse_transform(Xi)
ax.scatter(*X2.T,c='#44bbdd',edgecolor='#552211',alpha=0.5,marker='v')
ax.view_init(25,69)
plt.show()
จะเห็นว่าค่าแปลงกลับที่ได้นี้เมื่อมาวาดในระบบพิกัดเดิมซึ่งเป็น ๓ มิติจะได้เป็นระนาบ เพราะเดิมทีเป็นข้อมูลที่ถูกลดรูปเหลือ ๒ มิติโดยทิ้งมิติที่สำคัญน้อยที่สุดไป
หากข้อมูลที่จะวิเคราะห์และแปลงเป็นตัวเดียวกันดังเช่นในตัวอย่างนี้สามารถใช้เมธอด fit_transform แทนที่จะใช้ fit แล้วค่อย transform อีกที
ลองสร้างข้อมูลใหม่คล้ายเดิม แต่แค่คราวนี้เปลี่ยนมาใช้ fit_transform แทน
np.random.seed(55)
X,_ = datasets.make_blobs(2000,n_features=3,centers=5,center_box=(0,14))
plt.figure(figsize=[6,6],dpi=100)
lim = {xyz+'lim': (X[:,i].max()-(X.max()-X.min()),X[:,i].max()) for i,xyz in enumerate('xyz')} # ขอบเขต
ax = plt.axes([0,0,1,1],projection='3d',**lim)
ax.scatter(*X.T,c='#bbdd44',edgecolor='#223366',alpha=0.5)
Xi = PCA(2).fit_transform(X) # ป้อนข้อมูลเพื่อให้ทำการวิเคราะห์ และแปลงทันที
plt.figure(dpi=100)
plt.axes(aspect=1)
plt.grid(ls=':',color='#663388')
plt.scatter(*Xi.T,c='#bbdd44',edgecolor='#223366',alpha=0.5)
plt.show()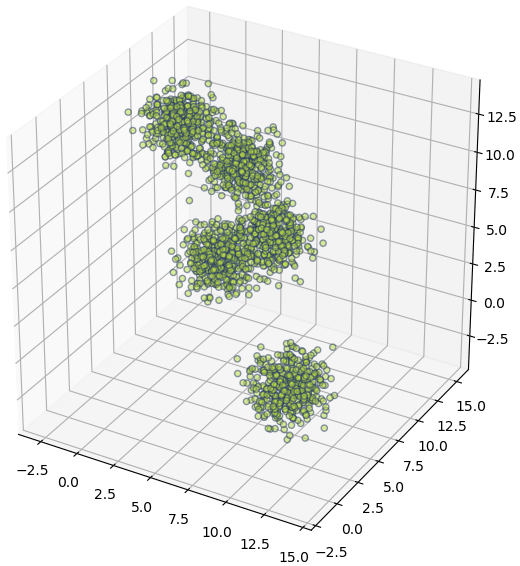
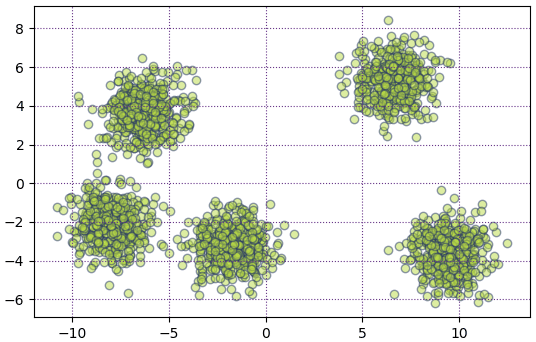
จะเห็นว่าพอใช้ fit_transform แล้วก็จะทำให้เขียนสั้นลง ลดขั้นตอนลงไปได้
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy