การวิเคราะห์องค์ประกอบหลัก (PCA) ด้วยการแยกค่าเอกฐาน (SVD)
เขียนเมื่อ 2019/09/16 20:50
แก้ไขล่าสุด 2022/07/11 12:33
ในบทความก่อนหน้านี้ได้เขียนถึงการวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) ไป https://phyblas.hinaboshi.com/20180727
โดยได้แสดงถึงว่าการวิเคราะห์องค์ประกอบหลักนั้นสามารถทำได้โดยหาเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector) ของเมทริกซ์ความแปรปรวนร่วมเกี่ยว (协方差矩阵, covariance matrix)
แต่ว่าในทางปฏิบัติแล้ว การคำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวเพื่อมาหากเวกเตอร์ลักษณะเฉพาะนั้นเป็นสิ่งที่กินเวลามาก โดยเฉพาะถ้าข้อมูลมีขนาดใหญ่
ในทางปฏิบัติแล้ว วิธีที่มักใช้แทนก็คือ การแยกค่าเอกฐาน (奇异值分解, singular value decomposition) หรือนิยมเรียกย่อๆว่า SVD
การทำ SVD นั้นง่ายกว่าการคำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวโดยตรง แต่สามารถได้ผลลัพธ์แบบเดียวกันนี้
หากใครใช้ฟังก์ชัน sklearn.decomposition.PCA ใน sklearn ที่จริงแล้วภายในนั้นก็คำนวณด้วย SVD เหมือนกัน
SVD คือการนำเมทริกซ์มาแยกเป็น ๓ ส่วน
X = UΣV*
โดยที่ X เป็นเมทริกซ์เดิม สมมุติว่ามี n×m (n แถว m หลัก)
U เป็นเมทริกซ์ขนาด n×n
Σ เป็นเมทริกซ์ขนาด n×m
V เป็นเมทริกซ์ขนาด m×m
โดยที่สัญลักษณ์ * หมายถึงเมทริกซ์สลับเปลี่ยนสังยุค (共轭转置, conjugate transpose)
ในที่นี้ขอมองข้ามเรื่องจำนวนจินตภาพไปเพราะใช้แต่เมทริกซ์ที่มีค่าเป็นจำนวนจริงอยู่แล้ว ดังนั้นไม่ต้องสนเรื่องการสังยุค (conjugate) แบบนี้ * ก็เป็นแค่ T คือเมทริกซ์สับเปลี่ยน (transpose) ธรรมดา คือแค่สลับแถวกับหลัก
ทั้ง U และ V เป็นเมทริกซ์เชิงตั้งฉาก (正交矩阵, orthogonal matrix)
Σ เป็นเมทริกซ์ที่มีค่าเฉพาะตัวในแนวทแยง ที่เหลือเป็น 0
ค่าในแนวทแยงของ Σ เรียกว่าเป็นค่าเอกฐาน (奇异值, singular value)
ก่อนจะอธิบายรายละเอียดมากกว่านี้ลองมาทำให้เห็นภาพได้ชัดขึ้นโดยการเขียนโปรแกรมคำนวณด้วยไพธอนจริงๆสักหน่อย
numpy มีฟังก์ชัน np.linalg.svd สามารถคำนวน SVD ได้ทันที ฟังก์ชันนี้มีอยู่ใน scipy ด้วย คือ scipy.linalg.svd จะใช้อันไหนก็ได้
ลองสร้างเมทริกซ์ขนาด 6×4 ขึ้นมาแล้วใช้ฟังก์ชันนี้ทำการคำนวณ SVD
ได้
np.linalg.svd นั้นจะให้ค่าออก ๓ ตัว โดยตัวแรกก็คือ U
ส่วนตัวที่ ๒ ที่ได้คือค่าเอกฐาน (SV) ซึ่งเป็นอาเรย์มิติเดียวซึ่งเป็นค่าแนวทแยงของ Σ สามารถนำมาแปลงเป็นเมทริกซ์เป็นเมทริกซ์ Σ ทีหลังได้ โดยตัวที่เหลือก็มีแต่ 0
ส่วนตัวที่ ๓ คือ V* ซึ่งในกรณีที่เป็นจำนวนจริงก็แค่เอาเมทริกซ์มาสับเปลี่ยนแถวกับหลัก คือ VT ในที่นี้ใช้ตัวแปรเป็น W แทน
เพื่อให้เห็นภาพชัดไปอีกแบบ ลองเอามาวาดแสดงด้วยสี ให้สีอ่อนแสดงค่ามาก สีเข้มคือค่าน้อย
X

U

Σ
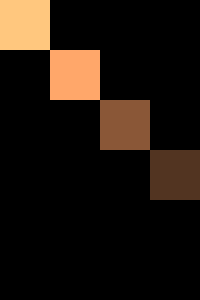
V*

V ที่ได้มานี้ก็คือเมทริกซ์ที่รวมเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector) ขององค์ประกอบ
ส่วน SV ก็คือตัวที่แสดงถึงอัตราความบ่งบอกความแปรปรวน (解释方差占比, variance explained ratio) ของแต่ละองค์ประกอบ
แล้ว UΣ ก็จะเทียบเท่ากับค่าของ X ในพิกัดขององค์ประกอบนั่นเอง เพราะ (UΣ)VT = X และ XV = UΣ
จากตรงนี้จะเห็นว่าผลที่ได้จาก SVD นั้นเทียบเคียงได้กับสิ่งที่เราต้องการจากการวิเคราะห์องค์ประกอบหลักเหมือนตอนที่คำนวณโดยหาเวกเตอร์ลักษณะเฉพาะของความปรวนร่วม
เพียงแต่ว่าวิธีการคำนวณเพื่อให้ได้มาซึ่งผลลัพธ์นั้นต่างกัน ความเร็วก็ต่างกันด้วย
เมื่อลองเปรียบเทียบดูแล้ว ถ้าจำนวนมิติของข้อมูลมีมากวิธีนี้จะคำนวณได้เร็วกว่า เพราะการคำนวณเมทริกซ์ความปรวนร่วมนั้นถ้ามิติมากจะต้องคำนวณสร้างเมทริกซ์ขนาดใหญ่เป็นจำนวนมิติกำลังสอง จำนวนมิติจึงมีผลต่อความเร็วอย่างมาก
ในขณะที่การคำนวณ SVD นั้นไม่ว่าจะนวนมิติมาก หรือจำนวนข้อมูลมาก ก็มีผลต่อความเร็วไม่ต่างกัน
ซึ่งที่จริงถ้าจำนวนมิติมีน้อยแล้วจำนวนของข้อมูลมีมาก วิธีการนี้กลับจะช้ากว่า
ตัวอย่างการใช้กับข้อมูลที่มีมิติมาก
ลองทดสอบกับข้อมูลที่มีมิติมากถึงหมื่นมิติดู โดยลดให้เหลือแค่ ๒ มิติแล้ววาดออกมาดู
ในตัวอย่างนี้จะสร้างคลาสในลักษณะเช่นเดียวกับที่สร้างไปใน https://phyblas.hinaboshi.com/20180727
เพียงแต่ว่าเปลี่ยนมาคำนวณด้วย SVD แทน
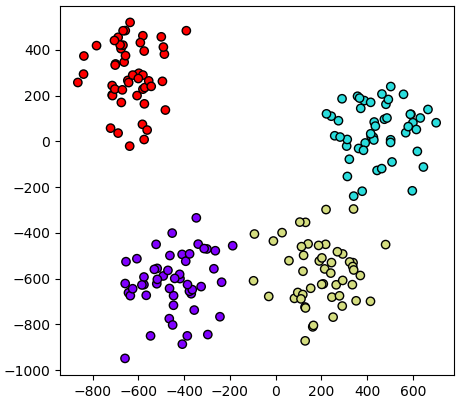
จะเห็นว่าแม้จะมีมากถึงหมื่นมิติแต่ก็คำนวณออกมาได้ในเวลาไม่นานนัก แต่ถ้าลองเปลี่ยนไปใช้วิธีสร้างเมทริกซ์ความแปรปรวนร่วมจะต้องคำนวณสร้างเมทริกซ์ขนาด "หมื่นคูณหมื่น" ซึ่งนอกจากจะช้าแล้วอาจ RAM ไม่พอได้ง่าย
การคำนวณ SVD ของแบบเมทริกซ์มากเลขศูนย์
บ่อยครั้งที่เวลาคำนวณหาองค์ประกอบหลักนั้นเราต้องการลดข้อมูลจากที่มีมิติมากให้เหลือมิติน้อย
ปกติแล้วเวลาคำนวณ SVD เราจะได้เมทริกซ์ V ขนาดจำนวนแถวและหลักเท่ากับจำนวนมิติของข้อมูล เช่นมี m มิติก็จะได้เมทริกซ์ m×m
แต่ว่าสุดท้ายก็จะคัดทิ้งเหลือองค์ประกอบเท่ากับจำนวนมิติที่ต้องการให้เหลือ คือ k ตัว นั่นคือใช้แค่เมทริกซ์ขนาด m×k เท่านั้น
หากรู้แน่อยู่แล้วว่าจะทิ้งเหลือกี่มิติ แบบนั้นถ้าใช้วิธีการคำนวณที่ไม่ต้องไปคำนวณในส่วนที่ยังไงเดี๋ยวก็จะต้องทิ้งอยู่แล้วเสียตั้งแต่แรกจะดีกว่า
ใน scipy มีวิธีที่จะทำแบบนั้นได้อยู่ คือใช้ฟังก์ชัน scipy.sparse.linalg.svds ในมอดูลย่อย scipy.sparse ซึ่งเป็นมอดูลย่อยที่เอาไว้จัดการเมทริกซ์ที่โล่งหร็อมแหร็ม
เมทริกซ์แบบนั้นเรียกว่า sparse matrix ส่วนศัพท์บัญญัติของไทยใช้คำว่า "เมทริกซ์มากเลขศูนย์" แม้จะไม่ได้แปลตรงตัว แต่ก็เป็นการแปลที่สื่อความหมายจริงๆ
sparse จริงๆถ้าแปลเป็นไทยก็คือ "หร็อมแหร็ม, เบาบาง, กระจัดกระจาย" ประมาณนั้น แต่ในที่นี้ก็คือหมายถึงเมทริกซ์ที่องค์ประกอบส่วนใหญ่เป็นเลข 0
รายละเอียดจะไม่พูดถึงมากตรงนี้ แต่สรุปง่ายๆก็คือ เมื่อใช้หลักการของเมทริกซ์มากเลขศูนย์ หรือเมทริกซ์หร็อมแหร็ม แล้วก็จะทำให้คำนวณ SVD ได้ด้วยความเร็วสูงขึ้นมาก
เราสามารถใช้ฟังก์ชัน scipy.sparse.linalg.svds แทน np.linalg.svd ได้
วิธีการใช้คล้ายๆกับ np.linalg.svd แต่ต่างกันตรงที่เราต้องกำหนดจำนวนมิติที่ต้องการเหลือไว้ตั้งแต่แรกเลย โดยใส่เป็นค่าอาร์กิวเมนต์ตัวที่ ๒ หรือจะใส่คีย์เวิร์ดเป็น k= ก็ได้
ตัวอย่าง ลองสร้างข้อมูลแสนมิติ แล้วคัดเหลือแค่ ๒ มิติ
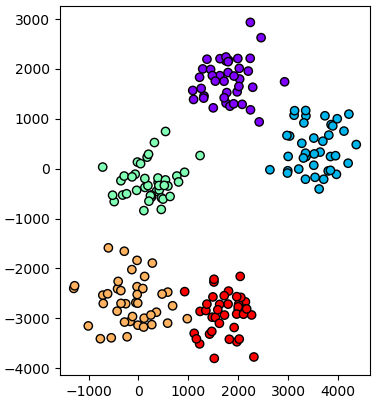
ถ้ามิติมากจริงๆยังไงก็ยิ่งช้า แต่ก็ถือว่าเป็นวิธีที่เร็วที่สุดแล้วหากต้องการวิเคราะห์องค์ประกอบของข้อมูลที่มีจำนวนมิติมากขนาดนั้น
เพียงแต่ถ้าข้อมูลไม่ได้มีขนาดใหญ่มาก การใช้ np.linalg.svd ก็ยังกลับจะเร็วกว่า
ถ้าใช้ฟังก์ชัน pca ของ sklearn นั้นภายในจะตรวจดูขนาดของข้อมูลให้อัตโนมัติ ถ้าข้อมูลใหญ่ก็จะใช้ sparse.linalg.svds ถ้าข้อมูลเล็กก็จะใช้ linalg.svd
ดังนั้นในการใช้งานจริงนั้นใช้ sklearn ไปเลยจะสะดวกที่สุด
สำหรับวิธีการใช้ sklearn เพื่อทำการวิเคราะห์องค์ประกอบหลักนั้นอ่านได้ใน https://phyblas.hinaboshi.com/20190921
โดยได้แสดงถึงว่าการวิเคราะห์องค์ประกอบหลักนั้นสามารถทำได้โดยหาเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector) ของเมทริกซ์ความแปรปรวนร่วมเกี่ยว (协方差矩阵, covariance matrix)
แต่ว่าในทางปฏิบัติแล้ว การคำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวเพื่อมาหากเวกเตอร์ลักษณะเฉพาะนั้นเป็นสิ่งที่กินเวลามาก โดยเฉพาะถ้าข้อมูลมีขนาดใหญ่
ในทางปฏิบัติแล้ว วิธีที่มักใช้แทนก็คือ การแยกค่าเอกฐาน (奇异值分解, singular value decomposition) หรือนิยมเรียกย่อๆว่า SVD
การทำ SVD นั้นง่ายกว่าการคำนวณเมทริกซ์ความแปรปรวนร่วมเกี่ยวโดยตรง แต่สามารถได้ผลลัพธ์แบบเดียวกันนี้
หากใครใช้ฟังก์ชัน sklearn.decomposition.PCA ใน sklearn ที่จริงแล้วภายในนั้นก็คำนวณด้วย SVD เหมือนกัน
SVD คือการนำเมทริกซ์มาแยกเป็น ๓ ส่วน
X = UΣV*
โดยที่ X เป็นเมทริกซ์เดิม สมมุติว่ามี n×m (n แถว m หลัก)
U เป็นเมทริกซ์ขนาด n×n
Σ เป็นเมทริกซ์ขนาด n×m
V เป็นเมทริกซ์ขนาด m×m
โดยที่สัญลักษณ์ * หมายถึงเมทริกซ์สลับเปลี่ยนสังยุค (共轭转置, conjugate transpose)
ในที่นี้ขอมองข้ามเรื่องจำนวนจินตภาพไปเพราะใช้แต่เมทริกซ์ที่มีค่าเป็นจำนวนจริงอยู่แล้ว ดังนั้นไม่ต้องสนเรื่องการสังยุค (conjugate) แบบนี้ * ก็เป็นแค่ T คือเมทริกซ์สับเปลี่ยน (transpose) ธรรมดา คือแค่สลับแถวกับหลัก
ทั้ง U และ V เป็นเมทริกซ์เชิงตั้งฉาก (正交矩阵, orthogonal matrix)
Σ เป็นเมทริกซ์ที่มีค่าเฉพาะตัวในแนวทแยง ที่เหลือเป็น 0
ค่าในแนวทแยงของ Σ เรียกว่าเป็นค่าเอกฐาน (奇异值, singular value)
ก่อนจะอธิบายรายละเอียดมากกว่านี้ลองมาทำให้เห็นภาพได้ชัดขึ้นโดยการเขียนโปรแกรมคำนวณด้วยไพธอนจริงๆสักหน่อย
numpy มีฟังก์ชัน np.linalg.svd สามารถคำนวน SVD ได้ทันที ฟังก์ชันนี้มีอยู่ใน scipy ด้วย คือ scipy.linalg.svd จะใช้อันไหนก็ได้
ลองสร้างเมทริกซ์ขนาด 6×4 ขึ้นมาแล้วใช้ฟังก์ชันนี้ทำการคำนวณ SVD
import numpy as np
X = np.arange(-4,20).reshape(6,4)/2
U,sv,W = np.linalg.svd(X)
Sigma = np.zeros_like(X)
Sigma[:len(sv),:len(sv)] = np.diag(sv)
print('X=\n%s'%X)
print('U=\n%s'%U)
print('Σ=\n%s'%Sigma)
print('V*=\n%s'%W)ได้
X=
[[-0.9330098 -1.2272592 -1.1769271 -0.71982633]
[-2.00659432 2.39830423 0.60754422 -0.90707789]
[-0.00334835 0.71909839 0.4503522 -1.11424495]
[-0.25129929 1.69495859 0.49591245 2.07755182]
[-0.60816189 -0.84689852 0.96693315 -1.37090087]
[-0.91821157 -1.25774444 -0.40389328 -1.07915852]]
U=
[[ 0.40403946 -0.13452204 0.65586452 0.11819427 -0.195199 -0.58002167]
[-0.4338776 -0.81503693 0.21835986 0.09622186 0.29604682 0.05368089]
[-0.03959412 -0.3152936 -0.42657657 0.41880222 -0.72824513 -0.106388 ]
[-0.63333423 0.17706933 0.29491611 -0.48910041 -0.48374194 -0.08563415]
[ 0.28073123 -0.35767022 -0.41518736 -0.70846344 0.02561177 -0.34395498]
[ 0.40867147 -0.2427489 0.28431862 -0.24543126 -0.33053053 0.72369647]]
Σ=
[[4.05145648 0. 0. 0. ]
[0. 3.40844577 0. 0. ]
[0. 0. 1.78739278 0. ]
[0. 0. 0. 1.06649963]
[0. 0. 0. 0. ]
[0. 0. 0. 0. ]]
V*=
[[ 0.02639931 -0.83676923 -0.23809852 -0.49237123]
[ 0.63311362 -0.3250715 -0.18742535 0.67702837]
[-0.6329527 -0.05263584 -0.67214738 0.38054993]
[ 0.44479334 0.43746456 -0.67557289 -0.39291846]]np.linalg.svd นั้นจะให้ค่าออก ๓ ตัว โดยตัวแรกก็คือ U
ส่วนตัวที่ ๒ ที่ได้คือค่าเอกฐาน (SV) ซึ่งเป็นอาเรย์มิติเดียวซึ่งเป็นค่าแนวทแยงของ Σ สามารถนำมาแปลงเป็นเมทริกซ์เป็นเมทริกซ์ Σ ทีหลังได้ โดยตัวที่เหลือก็มีแต่ 0
ส่วนตัวที่ ๓ คือ V* ซึ่งในกรณีที่เป็นจำนวนจริงก็แค่เอาเมทริกซ์มาสับเปลี่ยนแถวกับหลัก คือ VT ในที่นี้ใช้ตัวแปรเป็น W แทน
เพื่อให้เห็นภาพชัดไปอีกแบบ ลองเอามาวาดแสดงด้วยสี ให้สีอ่อนแสดงค่ามาก สีเข้มคือค่าน้อย
import matplotlib.pyplot as plt
for i,(a,s) in enumerate(zip([X,U,Sigma,W],['X','U','Σ','V*'])):
plt.figure(figsize=a.T.shape,dpi=50)
plt.axes([0,0,1,1])
plt.imshow(a,cmap='copper')
plt.axis('off')
plt.savefig('SVD_%s.png'%s)
plt.close()X

U

Σ
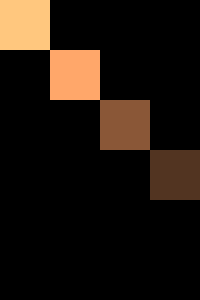
V*

V ที่ได้มานี้ก็คือเมทริกซ์ที่รวมเวกเตอร์ลักษณะเฉพาะ (本征向量, eigenvector) ขององค์ประกอบ
ส่วน SV ก็คือตัวที่แสดงถึงอัตราความบ่งบอกความแปรปรวน (解释方差占比, variance explained ratio) ของแต่ละองค์ประกอบ
แล้ว UΣ ก็จะเทียบเท่ากับค่าของ X ในพิกัดขององค์ประกอบนั่นเอง เพราะ (UΣ)VT = X และ XV = UΣ
จากตรงนี้จะเห็นว่าผลที่ได้จาก SVD นั้นเทียบเคียงได้กับสิ่งที่เราต้องการจากการวิเคราะห์องค์ประกอบหลักเหมือนตอนที่คำนวณโดยหาเวกเตอร์ลักษณะเฉพาะของความปรวนร่วม
เพียงแต่ว่าวิธีการคำนวณเพื่อให้ได้มาซึ่งผลลัพธ์นั้นต่างกัน ความเร็วก็ต่างกันด้วย
เมื่อลองเปรียบเทียบดูแล้ว ถ้าจำนวนมิติของข้อมูลมีมากวิธีนี้จะคำนวณได้เร็วกว่า เพราะการคำนวณเมทริกซ์ความปรวนร่วมนั้นถ้ามิติมากจะต้องคำนวณสร้างเมทริกซ์ขนาดใหญ่เป็นจำนวนมิติกำลังสอง จำนวนมิติจึงมีผลต่อความเร็วอย่างมาก
ในขณะที่การคำนวณ SVD นั้นไม่ว่าจะนวนมิติมาก หรือจำนวนข้อมูลมาก ก็มีผลต่อความเร็วไม่ต่างกัน
ซึ่งที่จริงถ้าจำนวนมิติมีน้อยแล้วจำนวนของข้อมูลมีมาก วิธีการนี้กลับจะช้ากว่า
ตัวอย่างการใช้กับข้อมูลที่มีมิติมาก
ลองทดสอบกับข้อมูลที่มีมิติมากถึงหมื่นมิติดู โดยลดให้เหลือแค่ ๒ มิติแล้ววาดออกมาดู
ในตัวอย่างนี้จะสร้างคลาสในลักษณะเช่นเดียวกับที่สร้างไปใน https://phyblas.hinaboshi.com/20180727
เพียงแต่ว่าเปลี่ยนมาคำนวณด้วย SVD แทน
from sklearn import datasets
class WikhroOngprakopLak:
def rianru(self,X):
_,sv,W = np.linalg.svd(X)
self.ver = sv/sv.sum()
self.V = W.T
def plaeng(self,X):
return X.dot(self.V)
def rianru_plaeng(self,X):
self.rianru(X)
return self.plaeng(X)
np.random.seed(2)
X,z = datasets.make_blobs(200,n_features=10000,centers=4,cluster_std=50)
wol = WikhroOngprakopLak()
wol.rianru(X)
Xi = wol.plaeng(X)[:,:2]
plt.axes(aspect=1)
plt.scatter(*Xi.T,c=z,cmap='rainbow',edgecolor='k')
plt.show()
จะเห็นว่าแม้จะมีมากถึงหมื่นมิติแต่ก็คำนวณออกมาได้ในเวลาไม่นานนัก แต่ถ้าลองเปลี่ยนไปใช้วิธีสร้างเมทริกซ์ความแปรปรวนร่วมจะต้องคำนวณสร้างเมทริกซ์ขนาด "หมื่นคูณหมื่น" ซึ่งนอกจากจะช้าแล้วอาจ RAM ไม่พอได้ง่าย
การคำนวณ SVD ของแบบเมทริกซ์มากเลขศูนย์
บ่อยครั้งที่เวลาคำนวณหาองค์ประกอบหลักนั้นเราต้องการลดข้อมูลจากที่มีมิติมากให้เหลือมิติน้อย
ปกติแล้วเวลาคำนวณ SVD เราจะได้เมทริกซ์ V ขนาดจำนวนแถวและหลักเท่ากับจำนวนมิติของข้อมูล เช่นมี m มิติก็จะได้เมทริกซ์ m×m
แต่ว่าสุดท้ายก็จะคัดทิ้งเหลือองค์ประกอบเท่ากับจำนวนมิติที่ต้องการให้เหลือ คือ k ตัว นั่นคือใช้แค่เมทริกซ์ขนาด m×k เท่านั้น
หากรู้แน่อยู่แล้วว่าจะทิ้งเหลือกี่มิติ แบบนั้นถ้าใช้วิธีการคำนวณที่ไม่ต้องไปคำนวณในส่วนที่ยังไงเดี๋ยวก็จะต้องทิ้งอยู่แล้วเสียตั้งแต่แรกจะดีกว่า
ใน scipy มีวิธีที่จะทำแบบนั้นได้อยู่ คือใช้ฟังก์ชัน scipy.sparse.linalg.svds ในมอดูลย่อย scipy.sparse ซึ่งเป็นมอดูลย่อยที่เอาไว้จัดการเมทริกซ์ที่โล่งหร็อมแหร็ม
เมทริกซ์แบบนั้นเรียกว่า sparse matrix ส่วนศัพท์บัญญัติของไทยใช้คำว่า "เมทริกซ์มากเลขศูนย์" แม้จะไม่ได้แปลตรงตัว แต่ก็เป็นการแปลที่สื่อความหมายจริงๆ
sparse จริงๆถ้าแปลเป็นไทยก็คือ "หร็อมแหร็ม, เบาบาง, กระจัดกระจาย" ประมาณนั้น แต่ในที่นี้ก็คือหมายถึงเมทริกซ์ที่องค์ประกอบส่วนใหญ่เป็นเลข 0
รายละเอียดจะไม่พูดถึงมากตรงนี้ แต่สรุปง่ายๆก็คือ เมื่อใช้หลักการของเมทริกซ์มากเลขศูนย์ หรือเมทริกซ์หร็อมแหร็ม แล้วก็จะทำให้คำนวณ SVD ได้ด้วยความเร็วสูงขึ้นมาก
เราสามารถใช้ฟังก์ชัน scipy.sparse.linalg.svds แทน np.linalg.svd ได้
วิธีการใช้คล้ายๆกับ np.linalg.svd แต่ต่างกันตรงที่เราต้องกำหนดจำนวนมิติที่ต้องการเหลือไว้ตั้งแต่แรกเลย โดยใส่เป็นค่าอาร์กิวเมนต์ตัวที่ ๒ หรือจะใส่คีย์เวิร์ดเป็น k= ก็ได้
ตัวอย่าง ลองสร้างข้อมูลแสนมิติ แล้วคัดเหลือแค่ ๒ มิติ
from scipy.sparse.linalg import svds
np.random.seed(137)
X,z = datasets.make_blobs(200,n_features=100000,centers=5,cluster_std=80)
U,sv,W = svds(X,2)
Xi = X.dot(W.T)
plt.axes(aspect=1)
plt.scatter(*Xi.T,c=z,cmap='rainbow',edgecolor='k')
plt.show()
ถ้ามิติมากจริงๆยังไงก็ยิ่งช้า แต่ก็ถือว่าเป็นวิธีที่เร็วที่สุดแล้วหากต้องการวิเคราะห์องค์ประกอบของข้อมูลที่มีจำนวนมิติมากขนาดนั้น
เพียงแต่ถ้าข้อมูลไม่ได้มีขนาดใหญ่มาก การใช้ np.linalg.svd ก็ยังกลับจะเร็วกว่า
ถ้าใช้ฟังก์ชัน pca ของ sklearn นั้นภายในจะตรวจดูขนาดของข้อมูลให้อัตโนมัติ ถ้าข้อมูลใหญ่ก็จะใช้ sparse.linalg.svds ถ้าข้อมูลเล็กก็จะใช้ linalg.svd
ดังนั้นในการใช้งานจริงนั้นใช้ sklearn ไปเลยจะสะดวกที่สุด
สำหรับวิธีการใช้ sklearn เพื่อทำการวิเคราะห์องค์ประกอบหลักนั้นอ่านได้ใน https://phyblas.hinaboshi.com/20190921
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> scipy