ต่อจาก บทที่ ๓

ในบทนี้จะว่าด้วยเรื่องการแจกแจงของความน่าจะเป็น โดยจะพิจารณาเฉพาะกรณีของค่าแบบไม่ต่อเนื่องก่อน สำหรับค่าแบบต่อเนื่องจะไปเขียนในบทที่ ๘




ตัวแปรสุ่มและการแจกแจงความน่าจะเป็น

เมื่อพิจารณาความน่าจะเป็นของเหตุการณ์บางอย่างที่แต่ละเหตุการณ์มีค่าเป็นตัวเลข เช่นทอยลูกเต๋าก็มี ๖​ หน้า อาจได้แต้ม 1,2,3,4,5,6 หรือแม้แต่การโยนเหรียญหัวก้อย อาจถือว่าได้หัวเป็น 1 ก้อยเป็น 0

ปริมาณที่มีค่าไม่แน่นอน อาจเป็นเท่าไหร่ก็ได้ขึ้นอยู่กับความน่าจะเป็นแบบนี้ เรียกว่าเป็น ตัวแปรสุ่ม (随机变量, random variable)

เช่นแต้มลูกเต๋าที่ทอยได้อาจออกมาเป็น 1,2,3,4,5,6 ถ้าเป็นลูกเต๋าทั่วไปที่โอกาสออกทุกหน้าเท่ากันคือ 1/6 อาจแจกแจงได้ในลักษณะนี้



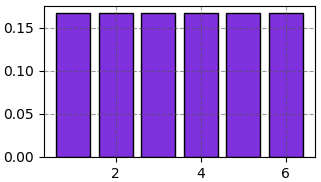
หรือถ้าหากเป็นลูกเต๋าที่มีการใส่ลูกเล่นบางอย่างทำให้แต่ละหน้ามีโอกาสได้ไม่เท่ากัน เช่น P(1)=1/10, P(2)=2/10, P(3)=1/10, P(4)=2/10, P(5)=3/10, P(6)=1/10 อาจเขียนการแจกแจงออกมาได้ในลักษณะนี้


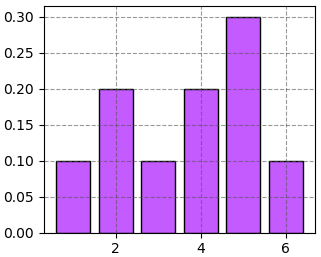
(ภาพ 4.2)

ตัวแปรสุ่มเป็นสิ่งที่ไม่รู้ค่าแน่ชัด ได้แค่พิจารณาว่าความน่าจะเป็นที่จะเป็นค่าเท่าใดมีมากแค่ไหน ดังนั้นลักษณะของการแจกแจงความน่าจะเป็นนั้นจึงเป็นคุณสมบัติที่สำคัญของตัวแปรสุ่ม




ค่าคาดหมายของตัวแปรสุ่ม

ค่าของตัวแปรสุ่มนั้นมีความไม่แน่นอน อย่างไรก็ตาม ถ้าหากมีการสุ่มค่าของตัวแปรสุ่มเดิมนั้นหลายครั้ง ค่าเฉลี่ยของค่าที่ได้ก็อาจลู่เข้าสู่ค่าที่แน่นอนค่าหนึ่ง ค่านั้นเรียกว่า ค่าคาดหมาย (期待值, expected value)

ค่าคาดหมายคำนวณได้จากผลรวมของผลคูณระหว่างค่าและความหนาแน่นของความเป็นไปได้ที่จะได้ค่านั้น

ค่าคาดหมายมักเขียนแทนด้วย E(ค่า) เมื่อเขียนเป็นสูตรคำนวณก็จะได้ว่า


ในที่นี้ k คือค่าแต่ละค่าที่มีความน่าจะเป็นอยู่ และ P(X=k) คือความน่าจะเป็นที่จะเป็นค่านั้น

เช่นกรณีทอยลูกเต๋าก็จะได้ว่า


ถ้า X เป็นแต้มที่ทอยได้บนลูกเต๋า ในกรณีลูกเต๋าที่ทุกหน้ามีโอกาสได้เท่ากันก็จะได้ค่าคาดหมายเป็น


สามารถลองพิสูจน์ได้โดยลองทอยลูกเต๋าดูจริงๆหลายๆครั้ง จะพบว่าค่าเฉลี่ยที่ได้ก็จะอยู่ที่ประมาณ 3.5 หรือก็คือมีแต้มรวมอยู่ที่ 3.5×n เมื่อ n เป็นจำนวนครั้งที่โยน

ลองทดลองสุ่มดูโดยใช้ฟังก์ชัน randint() ในมอดูล random ใช้สุ่มจำนวนเต็มในช่วงที่กำหนด

import random
n = 1000 # จำนวนครั้ง
x_ruam = 0 # ผลรวม บวกเพิ่มในแต่ละรอบ
for i in range(1,n+1):
    x = random.randint(1,6) # สุ่มค่าตั้งแต่ 1 ถึง 6
    print(f'รอบที่ {i} ได้ {x}') # แสดงค่าที่สุ่มได้ในแต่ละรอบ
    x_ruam += x
print('x รวมเป็น', x_ruam)
print('x เฉลี่ยเป็น', x_ruam/n)

ผลที่ได้จะออกมาในลักษณะนี้ (อาจต่างไปขึ้นอยู่กับผลการสุ่ม)

รอบที่ 1 ได้ 5
รอบที่ 2 ได้ 3
...
...(รอบอื่นๆ ขอละไว้)
...
รอบที่ 999 ได้ 6
รอบที่ 1000 ได้ 4
x รวมเป็น 3532
x เฉลี่ยเป็น 3.532

ผลที่ได้ควรจะได้ x เฉลี่ยอยู่ที่ประมาณ 3.5 ลองรันทดสอบดูหลายๆครั้งได้ และยิ่งเพิ่มจำนวน n ก็ยิ่งมีโอกาสได้ใกล้เคียงนี้มากขึ้น แต่ถ้าจำนวน n น้อยลงอาจได้ค่าที่ต่างไปจาก 3.5 มาก

แต่ถ้าเป็นในกรณีที่ลูกเต๋าแต่ละหน้ามีโอกาสออกไม่เท่ากัน เช่นมีการกระจายแบบในภาพ 4.2 แบบนี้ก็จะได้ค่าคาดหมายเป็น


ลองจำลองกรณีแบบนี้โดยใช้การเขียนโปรแกรมดู สำหรับกรณีที่ความน่าจะเป็นของแต่ละตัวเลขไม่เท่ากันแบบนี้อาจใช้ฟังก์ชัน choice() โดยใส่ลิสต์ของค่าที่ต้องการไปตามสัดส่วนจำนวนที่มีโอกาสออก

import random
p = [1,2,2,3,4,4,5,5,5,6] # ตัวเลือกที่มีโอกาสออก
n = 1000 # จำนวนครั้ง
x_ruam = 0 # ผลรวม บวกเพิ่มในแต่ละรอบ
for i in range(n):
    x = random.choice(p) # สุ่มค่าจากลิสต์ที่เตรียมไว้
    print(f'รอบที่ {i} ได้ {x}') # แสดงค่าที่สุ่มได้ในแต่ละรอบ
    x_ruam += x
print('x รวมเป็น', x_ruam)
print('x เฉลี่ยเป็น', x_ruam/n)

ผลที่ได้คราวนี้ค่าเฉลี่ยควรจะอยู่ที่ประมาณ 3.7 และผลรวมอยู่ที่ประมาณ 3700




ค่าคาดหมายของค่าที่คำนวณจากตัวแปรสุ่ม

เมื่อมีการนำตัวแปรสุ่มมาใช้คำนวณอะไรบางอย่าง ค่าที่ได้ก็จะมีความไม่แน่นอน จึงเป็นตัวแปรสุ่มเช่นกัน และก็จะมีการแจกแจงความน่าจะเป็นเช่นกัน แต่ค่าคาดหมายของค่าใหม่ที่ได้นั้นเป็นสิ่งที่สามารถคำนวณได้ไม่ยาก

ถ้า g(X) เป็นฟังก์ชันอะไรบางอย่างของ X ค่าคาดหมายสามารถคำนวณได้เช่นเดียวกับเมื่อคำนวณค่าคาดหมายของ X เพียงแค่เปลี่ยน X เป็น g(X)


ค่าคาดหมายของ 2 ตัวแปรที่บวกกันอยู่สามารถแยกออกมาได้

เช่น ค่าคาดหมายของกำลังสองของแต้มบนลูกเต๋าที่มีความน่าจะเป็นของทั้ง ๖ หน้าเท่ากัน


ลองเขียนโค้ดเพื่อทดลองบวกหาค่าดูจริงๆได้

import random
n = 10000 # จำนวนครั้ง
x2_ruam = 0 # ผลรวมของ x**2 บวกเพิ่มในแต่ละรอบ
for i in range(1,n+1):
    x = random.randint(1,6) # สุ่มค่าตั้งแต่ 1 ถึง 6
    x2_ruam += x**2
print('x รวมเป็น', x2_ruam) # ได้ 152582
print('x เฉลี่ยเป็น', x2_ruam/n) # ได้ 15.2582

ผลที่ได้ใกล้เคียงกับที่คำนวณไว้



ค่าคาดหมายของผลบวกระหว่างตัวแปรสุ่มสามารถแยกคิดได้

เมื่อ X และ Y เป็นตัวแปรสุ่ม จะได้ว่า


และค่าคงที่ใดๆที่บวกหรือคูณ X อยู่ สามารถดึงออกมาจากค่าคาดหมายได้ ดังนั้นเมื่อ c เป็นค่าคงที่ใดๆ ได้ว่า


และ


นั่นคือคิดค่าคาดหมายของ X เสร็จแล้วค่อยเอามาบวกหรือคูณค่าคงที่ได้

แต่ผลคูณระหว่างตัวแปรสุ่มจะสามารถแยกได้ในกรณีที่ตัวแปรทั้ง 2 มีความน่าจะเป็นที่เป็นอิสระต่อกันเท่านั้น

นั่นคือ ถ้า X และ Y เป็นตัวแปรสุ่มที่เป็นอิสระต่อกัน จะได้ว่า


ตัวอย่างเช่นค่าคาดหมายของผลคูณระหว่างลูกเต๋า 2 ลูก แต่ละลูกมีค่าคาดหมายเป็น 3.5 และค่าของลูกหนึ่งไม่ได้มีผลต่ออีกลูก ดังนั้นจึงได้ว่า


แต่ถ้าไม่เป็นอิสระต่อกันก็ไม่สามารถแยกแบบนี้ได้




ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานของตัวแปรสุ่ม

นอกจากค่าคาดหมายแล้ว คุณสมบัติที่สำคัญอีกอย่างของตัวแปรสุ่มก็คือค่าความแปรปรวน (方差, variance) และส่วนเบี่ยงเบนมาตรฐาน (标准差, standard deviation) ซึ่งเป็นค่าที่บอกว่าการกระจายของค่ามีขอบเขตกว้างแค่ไหน

ค่าความแปรปรวนของตัวแปรสุ่ม X มักเขียนแทนด้วย V(X) แบบนี้

การคำนวณค่าความแปรปรวนต้องเริ่มจากคำนวณค่าคาดหมาย E(X) จากนั้นนำค่าคาดหมายนี้มาพิจารณา คำนวณค่าคาดหมายของผลต่างกำลังสองของค่าคาดหมาย


ส่วนค่าส่วนเบี่ยงเบนมาตรฐาน มักเขียนแทนด้วย σ (ซิกมาเล็ก) คือรากที่สองของความแปรปรวน

จะใช้ค่าความแปรปรวนหรือส่วนเบี่ยงเบนมาตรฐานก็ได้ ความหมายไม่ต่างกันมาก โดยส่วนเบี่ยงเบนมาตรฐานจะเห็นภาพได้ชัดกว่าเพราะจะมีหน่วยเดียวกับค่าที่พิจารณาอยู่ เพียงแต่การคำนวณจะต้องถอดรากสอง ในขณะที่ความแปรปรวนคำนวณง่ายกว่า สำหรับบางกรณีถ้าใช้แค่ค่าความแปรปรวนได้ก็จะประหยัดการคำนวณได้มากกว่า

เพื่อให้เห็นภาพว่าค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานนี้เป็นค่าที่บอกถึงอะไร มีไว้เพื่ออะไร ขอยกตัวอย่าง เช่นพิจารณาคะแนนสอบของนักเรียนห้องหนึ่ง มี 50 คน คะแนนให้เป็นเลขจำนวนเต็มตั้งแต่ 0 ถึง 10 มีการแจกแจงดังนี้



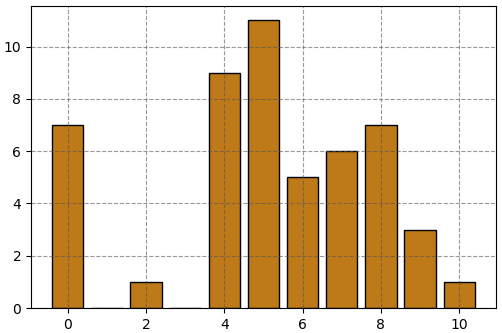
แบบนี้ถ้าถามว่าสุ่มใบคะแนนสอบขึ้นมาใบหนึ่งจะคาดได้ว่าจะได้ใบที่มีคะแนนเท่าไหร่ ค่านั้นก็คือค่าคาดหมาย

ลองเขียนโปรแกรมหาค่าคาดหมายได้ดังนี้

khanaen = [0,1,2,3,4,5,6,7,8,9,10] # ค่าคะแนน ไล่ตั้งแต่ 0 ถึง 10
mi = [7,0,1,0,9,11,5,6,7,3,1] # แต่ละคะแนนมีคนได้กี่คน
n = sum(mi) # จำนวนรวมมี 50 คน
khanaen_ruam = 0
for i in range(11):
    khanaen_ruam += khanaen[i]*mi[i]
E = khanaen_ruam/n
print('ค่าคาดหมาย =', E) # ได้ ค่าคาดหมาย = 5.16

จากนั้นค่าความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานก็คำนวนได้โดย

ruam = 0
for i in range(11):
    ruam += ((khanaen[i]-E)**2)*mi[i]
V = ruam/n
print('ความแปรปรวน =', V) # ได้ ความแปรปรวน = 7.1344
σ = V**0.5
print('ส่วนเบี่ยงเบนมาตรฐาน =', σ) # ได้ ส่วนเบี่ยงเบนมาตรฐาน = 2.671029763967448

เอาผลที่ได้มาวาดต่อเติมลงในแผนภูมิแท่งเพื่อจะเข้าใจความหมายของค่าคาดหมายและส่วนเบี่ยงเบนมาตรฐาน



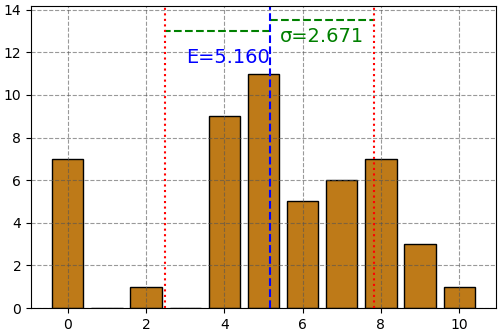
จะเห็นว่าค่าคาดหมายเป็นสิ่งที่แสดงถึงจุดใจกลางของการแจกแจงของค่า และส่วนเบี่ยงเบนมาตรฐานเป็นปริมาณที่แสดงให้เห็นภาพได้ว่าการกระจายของความน่าจะเป็นนั้นมากแค่ไหน

ถ้าลองเปลี่ยนข้อมูลชุดใหม่ซึ่งค่ามีการเกาะกลุ่มกันมาก ส่วนเบี่ยงเบนมาตรฐานก็จะน้อย



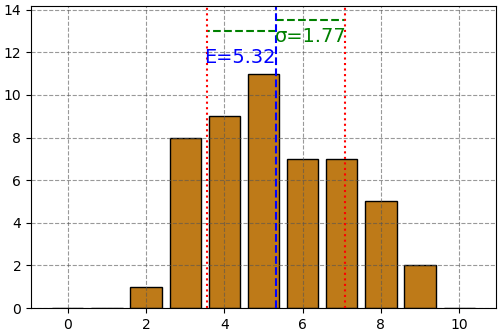
ในทางตรงข้าม ถ้าคะแนนกระจัดกระจายมาก ส่วนเบี่ยงเบนมาตรฐานก็จะมาก



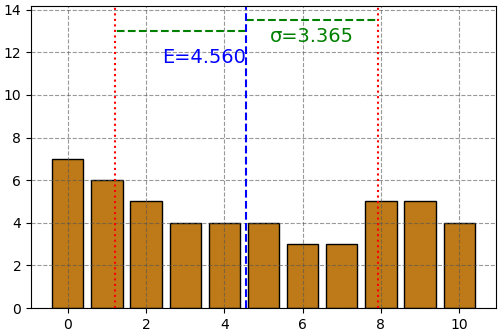
แบบนี้ต่อให้เราไม่ได้วาดภาพเพื่อแสดงการแจกแจง แค่ดูจากค่าคาดหมายกับส่วนเบี่ยงเบนมาตรฐานก็พอจะนึกภาพข้อมูลได้คร่าวๆแล้ว

ดังนั้นค่าคาดหมายกับส่วนเบี่ยงเบนมาตรฐาน (หรือความแปรปรวน) จึงเป็นคุณสมบัติที่สำคัญของตัวแปรสุ่ม มักถูกใช้งานอยู่อย่างกว้างขวาง




ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานของค่าที่คำนวณจากตัวแปรสุ่ม

หากค่าของตัวแปรสุ่มถูกบวกด้วยค่าคงที่ จะไม่มีผลต่อความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน

นั่นคือถ้า c เป็นค่าคงที่ จะได้ว่า


นั่นเพราะค่าคงที่ซึ่งมาเพิ่มให้กับทุกค่าเท่ากันหมดย่อมไม่มีผลเปลี่ยนแปลงการแจกแจงของค่า

แต่สำหรับกรณีที่คูณด้วยค่าคงที่ การแจกแจงก็เปลี่ยนแปลงโดยคูณเพิ่มไปด้วย ความแปรปรวนนั้นมีหน่วยเป็นยกกำลังสอง ดังนั้นค่าคงที่จึงยกกำลังสอง


ส่วนเบี่ยงเบนมาตรฐานจะได้เป็นค่าสัมบูรณ์ของค่าคงที่นั้น





กฎว่าด้วยจำนวนมาก

ดังที่ได้กล่าวไปแล้วว่าถ้าหากทำการสุ่มค่าหลายครั้ง ค่าเฉลี่ยของค่าที่ได้จะมีค่าเข้าใกล้ค่าคาดหมาย

นี่เป็นหลักการที่เรียกว่า กฎว่าด้วยจำนวนมาก (大数定律, law of large numbers)

อย่างเช่นเมื่อทอยลูกเต๋า ค่าคาดหมายคือ 3.5 ถ้าทอยแค่ไม่กี่ทีค่าเฉลี่ยที่ได้อาจต่างไปจาก 3.5 มาก แต่ถ้าทอยหลายๆลูกเข้าในที่สุดก็จะเข้าใกล้ 3.5

ลองเขียนโปรแกรมสุ่มค่าแต้มลูกเต๋าตั้งแต่ 1 ลูกไปจนถึง 2000 ลูก ทำซ้ำดู 20 ครั้ง

import random
# ทำซ้ำ 20 ครั้ง
for i in range(1,21):
    ruam = 0 # ผลรวม
    chalia = [] # ลิสต์เก็บค่าเฉลี่ยในแต่ละขั้น
    # ไล่ทำตั้งแต่ลูกแรก ไปจนถึงลูกที่ 2000
    for n in range(1,2000+1):
        ruam += random.randint(1,6) # บวกรวมไปเรื่อยๆ
        chalia += [ruam/n] # ค่าเฉลี่ยในแต่ละขั้นคือผลรวมหารด้วยจำนวนขณะนั้น
    
    # แสดงค่าเฉลี่ยตั้งแต่ใช้ 1 ลูกไปจนถึงใช้ 2000 ลูก ที่ได้ในแต่ละรอบ
    print('รอบที่ ',i,'ได้:\n',chalia)

ผลที่ได้เมื่อนำมาวาดกราฟก็จะออกมาในลักษณะนี้



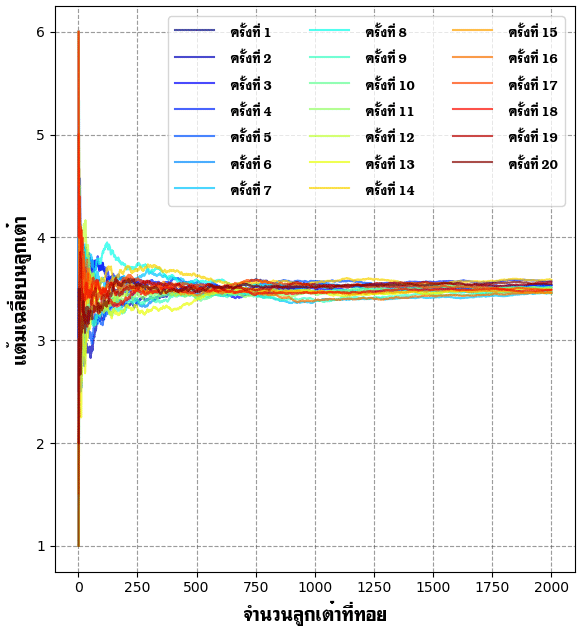
จะเห็นได้ว่าในแต่ละครั้งช่วงที่โยนไม่กี่ลูกค่าเฉลี่ยอาจกระจายอยู่ตั้งแต่ 1 ถึง 6 แต่ยิ่งโยนหลายลูกก็จะลู่เข้า 3.5 ไม่ว่าจะลองซ้ำกี่ครั้งก็เห็นผลแบบนี้

ทำไมยิ่งลองจำนวนมากแล้วค่าเฉลี่ยจะลู่เข้าสู่ค่าคาดหมาย ลองพิสูจน์ดูได้ดังนี้

ให้ X_i เป็นแต้มลูกเต๋าลูกที่ i ที่ทอยได้ ดังนั้นค่าเฉลี่ย X̄ ของแต้มลูกเต๋าเมื่อทอย n ครั้งจะได้


หากทดลองซ้ำหลายๆครั้ง แล้วคำนวณหาค่าคาดหมายของ X̄


ในเมื่อแต่ละครั้งที่ทอยก็มีโอกาสจะได้ค่าเป็นค่าคาดหมาย ดังนั้นค่าคาดหมายของผลรวมของทุกค่าก็คือค่าคาดหมายของ X คูณด้วยจำนวน n


ดังนั้นค่าคาดหมายของค่าเฉลี่ยก็เท่ากับค่าคาดหมายของตัวแปรสุ่มนั้นเอง

คำนวณค่าความแปรปรวนของ X̄ ก็ได้ในทำนองเดียวกัน


ระวังว่าในที่นี้ n ดึงออกมาจากใน V() กลายเป็น n² ตามหลักการคำนวณคูณกับค่าคงที่ของความแปรปรวน

จากผลจะเห็นได้ว่าค่าคาดหมายของค่าเฉลี่ยไม่ต่างไปจากค่าคาดหมายของตัวแปรสุ่มนั้น แต่ความแปรปรวนจะยิ่งลดลงเมื่อมีการทดลองมากขึ้น โดยแปรผกผันกับจำนวนครั้ง n

ถ้าพิจารณาค่าส่วนเบี่ยงเบนมาตรฐานก็จะเป็น


ดังนั้นกฎว่าด้วยจำนวนมากนี้นอกจากจะบอกว่าค่าเฉลี่ยของผลที่ได้จะลู่เข้่าสู่ค่าคาดหมายแล้ว ยังบอกอีกว่ายิ่งจำนวนที่ทดลองมากก็จะยิ่งลู่เข้ามาก โดยส่วนเบี่ยงเบนมาตรฐานจะแปรผกผันกับรากที่สองของจำนวนครั้ง n

ส่วนเบี่ยงเบนมาตรฐานลดลงก็คือมีการกระจัดกระจายของค่าลดลง ยิ่งเห็นได้ชัดว่าลู่เข้าสู่ค่าไหน

ซึ่งก็ตรงกับสามัญสำนึกในชีวิตประจำวันที่ว่ายิ่งทดลองซ้ำเป็นจำนวนมากก็ยิ่งมั่นใจในผลลัพธ์ได้มากขึ้น

แต่ว่าเนื่องจากเป็นรากที่สองของจำนวน n ดังนั้นจึงไม่ใช่เรื่องง่ายนัก เช่นว่าเพื่อจะให้ได้ผลที่แน่นอนขึ้น 10 เท่าก็ต้องทดลองถึง 100 ครั้ง เป็นต้น

ถ้าทดลองอนันต์ครั้ง คือ n -> ∞ แบบนี้ส่วนเบี่ยงเบนมาตรฐานก็เข้าสู่ 0 หมายความว่า X̄ เป็นค่านั้นแน่นอนไม่มีคลาดเคลื่อน

แต่ในชีวิตจริงไม่มีทางที่จะทดลองอะไรเป็นอนันต์ครั้งได้จริง ดังนั้นไม่ว่าจะวัดอะไรก็ตาม ย่อมมีความคลาดเคลื่อนเสมอ แค่เราสามารถลดความคลาดเคลื่อนได้โดยเพิ่มจำนวนครั้งที่ทดลอง



บทถัดไป >> บทที่ ๕

~ 自我介绍 ~

目录

从日本来的名言

python 模块 -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 机器学习 -- 神经网络

javascript

蒙古语

语言学

maya

概率论

与日本相关的日记

与中国相关的日记 -- 与北京相关的日记 -- 与香港相关的日记 -- 与澳门相关的日记

与台湾相关的日记

与北欧相关的日记

与其他国家相关的日记

qiita

其他日志

按类别分日志

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 查看日志

　 最近

　 推荐日志

各月日志

找更早以前的日志

ไทย

日本語

中文