ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๓: ความน่าจะเป็นก่อนและหลังเหตุการณ์และทฤษฎีบทของเบย์
เขียนเมื่อ 2020/07/25 19:07
แก้ไขล่าสุด 2024/10/03 19:36
ต่อจาก บทที่ ๒
ในบทนี้จะว่าด้วยความน่าจะเป็นที่เปลี่ยนแปลงไปตามเหตุการณ์ก่อนและหลังจากที่รู้ข้อมูลเพิ่มเติมหรือสถานการณ์เปลี่ยนแปลงไป ซึ่งตรงนี้จะนำไปสู่หลักการของความน่าจะเป็นและสถิติแบบเบส์
ความน่าจะเป็นก่อนและหลังเหตุการณ์
เมื่อพิจารณาถึงความน่าจะเป็นของเหตุการณ์บางอย่างอยู่ แต่เราเกิดรู้เงื่อนไขเพิ่มเติมหรือสถานการณ์บางอย่างได้เปลี่ยนแปลงไป แบบนั้นความน่าจะเป็นก็อาจเปลี่ยนแปลงไปได้
ยกตัวอย่างเช่น มีหลุมอยู่ 3 หลุม หนึ่งในนั้นมีสมบัติซ่อนอยู่
(囗)(囗)(国)
แบบนี้ถ้าเลือกโดยที่ไม่รู้อะไรเลยโอกาสที่จะเจอสมบัติก็คือ 1/3
ทีนี้สมมุติว่าพอดีเรามีเครื่องมือตรวจสอบ แต่เครื่องมือนี้ไม่ได้แม่นนัก ตรวจ 5 ครั้งจะผิดสักครั้งหนึ่ง นั่นคือความน่าจะเป็นที่จะผิดเป็น 1/5
พอเราลองเลือกหลุมหนึ่งจาก 3 หลุม แล้วใช้เครื่องตรวจสอบดูเครื่องตรวจบอกว่าหลุมนั้นมีสมบัติอยู่จริง
แบบนี้ความน่าจะเป็นที่หลุมที่เราเลือกนั้นจะมีสมบัติอยู่จริงๆจะกลายเป็นเท่าไหร่?
ค่อยๆพิจารณาโดยวาดรูปแบ่งพื้นที่ ประกอบ
เริ่มแรก โอกาสที่จะมีสมบัติอยู่จริงคือ 1/3 ก็แบ่งพื้นที่ออก 1:2 แบบนี้
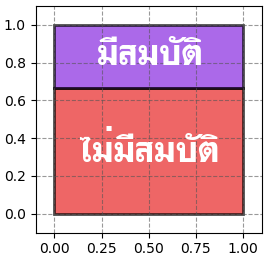
จากนั้นใช้เครื่องตรวจ โอกาสที่เครื่องจะบอกว่าตรวจเจอหรือไม่ขึ้นอยู่กับว่ามีสมบัติจริงหรือเปล่า โอกาสถูกเป็น 4/5 หมายความว่าถ้ามีสมบัติโอกาสที่ผลตรวจจะบอกว่าเจอก็เป็น 4/5 ของในนั้น แต่ถ้าในนั้นไม่มีสมบัติอยู่โอกาสที่ผลตรวจจะบอกว่าเจอก็เป็น 1/5 ลองวาดภาพแบ่งใหม่ได้ดังนี้
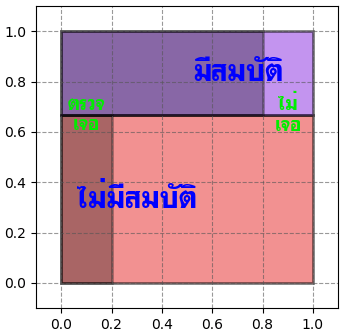
ทีนี้เราได้ใช้เครื่องมือตรวจแล้วเครื่องบอกว่าตรวจเจอ งั้นความเป็นไปได้ในส่วนที่ว่าตรวจไม่เจอก็หายไป เหลือแค่ตรงส่วนที่ตรวจเจอ
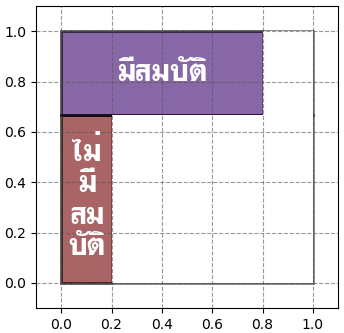
ดังนั้นโอกาสที่หลุมนั้นจะมีสมบัติอยู่จริงๆก็คือพื้นที่ส่วนที่เหลือและบอกว่ามีสมบัติ เทียบกับพื้นที่ทั้งหมดที่เหลืออยู่
ดังนั้นแสดงว่าหลังจากที่ได้ผลการตรวจมาแล้ว พบว่าความน่าจะเป็นที่จะมีสมบัติอยู่กลายเป็น 2/3
แสดงว่าแม้จะรู้ว่าเดิมทีโอกาสเจอสมบัติมีน้อยเป็นแค่ 1/3 เท่านั้น แต่ถ้าเชื่อตามที่เครื่องนี้บอก โอกาสก็กลายเป็น 2/3
แต่ในทางตรงกันข้าม ถ้าหากเครื่องตรวจบอกว่าไม่มี ก็จะกลายเป็นแบบนี้
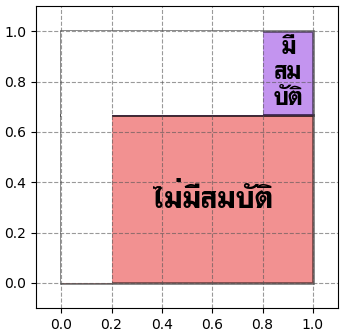
เท่ากับว่าจากที่เดิมความเป็นไปได้ก็น้อยอยู่แล้วพอเครื่องตรวจมาช่วยย้ำผลว่าไม่มี โอกาสที่จะมีก็เลยกลายเป็นริบหรี่กว่าเดิม
สรุปก็คือ เมื่อได้ข้อมูลเพิ่มเติม ไม่ว่าจะเป็นไปในทางใด ความน่าจะเป็นของเหตุการณ์ต่างๆก็จะเปลี่ยนแปลงไปได้
ความน่าจะเป็นจากข้อมูลเดิมที่มีอยู่ก่อนที่จะได้ข้อมูลใหม่เพิ่มเติมเรียกว่าเป็น ความน่าจะเป็นก่อนหน้า (先验概率, prior probability) หรือเป็นความน่าจะเป็นตั้งต้น
ส่วนความน่าจะเป็นหลังจากได้ข้อมูลใหม่มาแล้วจะเรียกว่า ความน่าจะเป็นภายหลัง (后验概率, posterior probability)
ในที่นี้ความน่าจะเป็นก่อนหน้าก็คือ 1/3 ส่วนความน่าจะเป็นภายหลัง กรณีที่เครื่องตรวจบอกว่าเจอจะเป็น 2/3 ถ้าเครื่องตรวจบอกว่าไม่เจอจะเป็น 1/9
ทฤษฎีบทของเบส์
จากตัวอย่างปัญหาข้างต้นนี้อาจดูซับซ้อน ต้องวาดภาพนึกภาพตาม ถ้าปัญหายิ่งซับซ้อนขึ้นก็จะยิ่งนึกภาพตามยากขึ้น ปัญหาส่วนใหญ่จะมานั่งวาดภาพไล่คิดตลอดแบบนี้ไม่ได้
แต่หากเข้าใจแล้วก็จะพบว่าการพิจารณาความน่าจะเป็นในลักษณะนี้ได้นำไปสู่ข้อสรุปที่อาจคำนวณเป็นสูตรได้ว่า
สมการนี้เรียกว่าทฤษฎีบทของเบส์ (贝叶斯定理, Bayes' theorem) เป็นสูตรที่มีประโยชน์เวลาที่ต้องการมองค้นย้อนจากผลไปหาเหตุ
ในกรณีตัวอย่างปัญหาหลุมสมบัติกับเครื่องตรวจสมบัติดังที่ยกมาข้างต้นนี้เรามีผลลัพธ์ก็คือผลการตรวจของเครื่องตรวจ แต่สิ่งที่ต้องการจะรู้ก็คือความเป็นไปได้ที่จะมีสมบัติอยู่จริงๆ
ในที่นี้หากให้ A เป็นเหตุการณ์ที่เครื่องตรวจบอกว่ามีสมบัติ ส่วน B เป็นเหตุการณ์ที่มีสมบัติอยู่จริง แบบนี้เมื่อแทนข้อมูลที่มีอยู่ลงไปในสมการนี้ก็จะสามารถคำนวณได้ทันที
P(A|B) ในที่นี้คือโอกาสที่เครื่องจะตรวจพบว่ามีสมบัติจริงๆในกรณีที่มีสมบัติอยู่จริง ซึ่งโจทย์ก็กำหนดมาว่าความแม่นของเครื่องเป็น 4/5
P(B) คือความน่าจะเป็นเดิมที่จะมีสมบัติอยู่จริง ซึ่งก็คือ 1/3
P(A) คือความน่าจะเป็นที่เครื่องจะตรวจเจอ ซึ่งก็คือผลรวมความน่าจะเป็นระหว่างกรณีที่ตรวจเจอทั้งที่ไม่มีสมบัติอยู่จริงและกรณีที่ตรวจเจอในขณะที่มีสมบัติอยู่จริง
เมื่อแทนลงในสมการแล้ว การคำนวณจึงออกมาเป็นดังที่แสดงในตัวอย่างข้างต้นนั่นเอง
ส่วนที่มีของสูตรนี้ก็คือมาจากความสัมพันธ์ระหว่างความน่าจะเป็นแบบมีเงื่อนไขกับความน่าจะเป็นร่วม นั่นคือ
ดังนั้น
เป็นสูตรที่มีที่มาที่ไปไม่ซับซ้อน แต่ใช้ประโยชน์ได้อย่างกว้างขวาง
ในที่นี้ P(B) คือความน่าจะเป็นก่อนหน้า ส่วน P(B|A) คือความน่าจะเป็นภายหลัง ดังนั้นประโยชน์ของสูตรนี้ก็คือทำให้เราสามารถคำนวณความน่าจะเป็นภายหลังได้จากความหน้าจะเป็นก่อนหน้าที่มีอยู่
ความน่าจะเป็นเปลี่ยนไปตามข้อมูลที่มี
จากแนวคิดข้างต้นนี้นำไปสู่หลักแนวคิดของ การอนุมานแบบเบส์ (贝叶斯推断, Bayesian inference)
คือการที่มองว่าความน่าจะเป็นจะเปลี่ยนไปตามข้อมูลที่เราได้มา และเปลี่ยนไปได้เรื่อยๆเมื่อมีข้อมูลใหม่เข้ามา ดังนั้นความน่าจะเป็นขึ้นอยู่กับข้อมูลที่เรารู้อยู่ขณะนั้น
อย่างไรก็ตาม ที่จริงแล้วเรื่องของความน่าจะเป็นนี้ออกจะเป็นเชิงปรัชญาที่มีการถกเถียงกันมากมายเช่นกัน โดยคนที่ค้านแนวคิดแบบเบส์จะมองว่าความน่าจะเป็นนั้นเป็นสิ่งที่อยู่ในตัวเหตุการณ์นั้นๆ ไม่ควรจะขึ้นกับสิ่งที่เรารู้
ปัญหาที่มักจะยกขึ้นมาก็คือ การที่ความน่าจะเป็นตั้งต้นที่ถูกกำหนดขึ้นนั้นมีผลต่อความน่าจะเป็นภายหลัง
แต่ความน่าจะเป็นตั้งต้นเองก็อาจเป็นสิ่งที่ขึ้นอยู่กับสิ่งที่เรารู้มาเช่นกัน
เช่นในตัวอย่างเรื่องหลุมสมบัติข้างต้นนี้ ถ้าหากข้อมูลเริ่มแรกที่เรามีนั้นเปลี่ยนไป เช่นว่าจริงๆแล้วใน 3 หลุมนี้มี 2 หลุมที่มีสมบัติอยู่ แบบนี้ความน่าจะเป็นเริ่มต้นจะกลายเป็น 2/3 ลองวาดภาพดูใหม่จะกลายเป็นแบบนี้
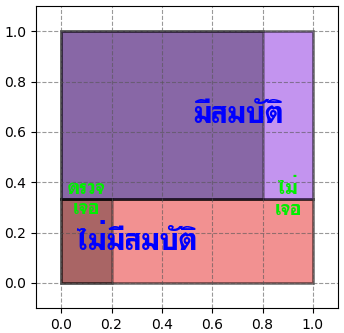
แบบนี้หลังจากที่ใช้เครื่องตรวจ (ซึ่งให้มีความแม่นเป็น 4/5 เท่าเดิม) แล้วเครื่องบอกว่ามีสมบัติอยู่ ความน่าจะเป็นก็จะกลายเป็น
ซึ่งต่างจากกรณีเดิมที่ค่าความน่าจะเป็นตั้งต้นเดิมเป็น 1/3 ซึ่งจะได้ผลความน่าจะเป็นภายหลังเป็น 2/3
และลองคิดอีกกรณี คือถ้าเครื่องตรวจบอกว่าไม่เจอก็จะเป็น
ซึ่งต่างจากกรณีที่ความน่าจะเป็นตั้งต้นเป็นแบบเดิมที่บอกว่าจะเป็น 1/9
แล้วถ้าหากข้อมูลเริ่มแรกบอกว่าทั้ง 3 หลุมมีสมบัติอยู่ล่ะ? แบบนี้จะใช้เครื่องตรวจหรือไม่ความน่าจะเป็นที่จะมีสมบัติก็เป็น 1 คือยังไงก็มีแน่นอน
ซึ่งจากมุมมองของหลักสถิติและความน่าจะเป็นแบบดั้งเดิมนั้นคือจะฟังดูแปลกที่ว่าการรับรู้ของคนไปมีผลให้ความน่าจะเป็นเปลี่ยนแปลงไปได้ ทั้งที่ผลของเหตุการณ์บางอย่างควรจะได้ถูกกำหนดตายตัวอยู่แล้วไม่ว่าเราจะรู้หรือไม่ก็ตาม
ดังนั้นจึงบอกว่าเรื่องของความน่าจะเป็นนั้นมีความเกี่ยวพันกับปรัชญา เมื่อคิดให้ดีโลกนี้ประหลาด พวกเรื่องเชิงปรัชญาเช่นนี้ ยิ่งคิดแล้วก็อาจจะยิ่งแปลกใจเหมือนจะยิ่งไม่เข้าใจอะไร
แต่ถึงอย่างนั้นก็เห็นได้ชัดว่าการรู้ข้อมูลอะไรมากขึ้นช่วยให้เราคาดเดาทำนายอะไรได้แม่นยำมากขึ้น แนวคิดแบบเบส์นี้จึงถูกใช้อย่างกว้างขวางในการวิจัยทางวิทยาศาสตร์
ยิ่งมีข้อมูลมากก็ยิ่งเรียนรู้และทำนายได้ถูกต้องขึ้น นี่เป็นพื้นฐานแนวคิดของการเรียนรู้ของเครื่องนั่นเอง ดังนั้นจะเห็นได้ถึงความเชื่อมโยงระหว่างความน่าจะเป็นของเบส์กับหลักการเรียนรู้ของเครื่อง
ความน่าจะเป็นภายหลังกลายเป็นความน่าจะเป็นก่อนหน้าของการทดลองครั้งต่อไป
ประโยชน์จากการอนุมานของเบส์ทำให้เราคำนวณความน่าจะเป็นของเหตุการณ์โดยดูจากข้อมูลเดิมที่มีและข้อมูลที่ได้มาใหม่
แล้วเมื่อได้ข้อมูลใหม่มาแล้วทำให้ความน่าจะเป็นเปลี่ยนแปลงไปอีก ความน่าจะเป็นภายหลังที่ได้นั้นสามารถเอามาใช้เป็นความน่าจะเป็นก่อนหน้าของการทดลองครั้งต่อไป และสามารถทำซ้ำๆไปเรื่อยๆซึ่งจะเห็นความเปลี่ยนแปลงของความน่าจะเป็นไปเรื่อยๆได้
เพื่อจะให้เห็นภาพมากขึ้นจึงขอยกอีกตัวอย่างหนึ่ง
สมมุติว่ามีไหอยู่ 2 ใบ ใส่บอลไว้ 10 ลูก ขนาดเท่ากันทั้งหมด ไห ก. มีสีเขียว 8 ลูก สีแดง 2 ลูก ไห ข. มีสีเขียว 4 ลูก สีแดง 6 ลูก
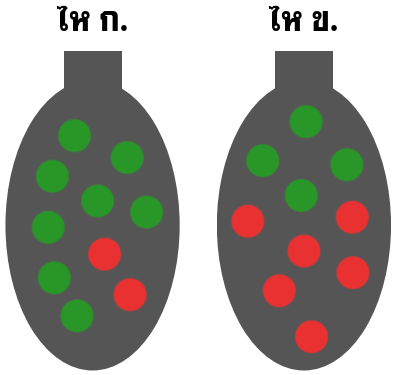
ถ้าหากว่าต้องสุ่มหยิบบอลขึ้นมาลูกหนึ่งจากไหใบหนึ่ง โดยเราไม่รู้ว่าไหใบไหนคือไห ก. หรือ ข. ความน่าจะเป็นที่จะหยิบได้ลูกสีเขียวเป็นเท่าใด?
และอีกคำถามคือ ถ้าผลประกฏว่าหยิบออกมาแล้วได้ลูกสีเขียว ถามว่าความน่าจะเป็นที่ไหใบนั้นจะเป็นไห ก. เป็นเท่าใด? และถ้าหยิบลูกบอลจากไหใบเดิมต่ออีกความน่าจะเป็นที่จะหยิบได้ลูกสีเขียวกลายเป็นเท่าใด?
ในตัวอย่างนี้ โอกาสหยิบได้บอลสีอะไรนั้นขึ้นอยู่กับว่าเราหยิบจากไหใบไหน แต่ปัญหาคือตอนแรกเราไม่รู้ด้วยซ้ำว่าไหที่เลือกเป็นไหใบไหน แบบนี้จึงต้องพิจารณาโอกาสที่จะเป็นไหแต่ละใบไปด้วย
จากข้อมูลที่ว่ามีใบหนึ่งเป็นไห ก. ใบหนึ่งเป็น ข. หมายความทั้ง 2 มีโอกาสเป็น 1/2 ทั้งคู่ แบบนี้
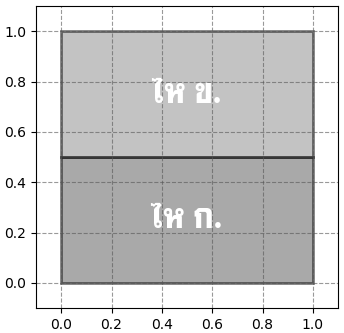
ทีนี้ถ้าหากหยิบไห ก. โอกาสได้สีเขียวคือ 8/10 ถ้าหยิบไห ข. โอกาสที่ได้สีเขียวคือ 4/10 ดังนั้นภาพจะกลายเป็นแบบนี้
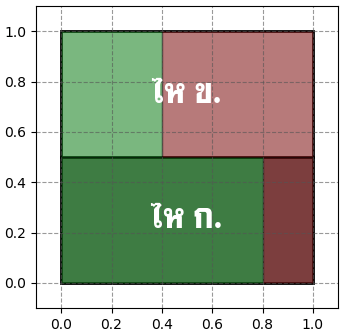
ดังนั้นจะได้ว่าโอกาสที่จะหยิบได้สีเขียวคือ
จากนั้นถ้าลองหยิบขึ้นมาลูกหนึ่งแล้วพบว่าได้สีเขียว ผลที่ได้นี้จะต้องมีผลต่อโอกาสที่จะเป็นไห ก. หรือ ข. โดยจะเกิดการตัดผลในส่วนที่หยิบได้สีแดงออก และพิจารณาส่วนที่เหลือ
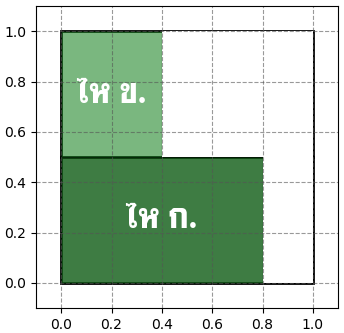
ดังนั้นความน่าจะเป็นที่จะเป็นไห ก. จึงกลายเป็น
เอาส่วนที่เหลือมาเขียนเป็นสัดส่วนพื้นที่ตามความน่าจะเป็นใหม่ได้แบบนี้
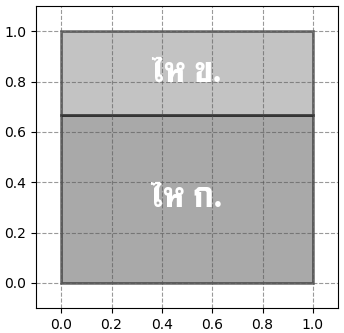
เมื่อหยิบลูกบอลจากไหใบเดิมอีกที ถ้าไหนี้เป็นไห ก. ก็จะเหลือสีเขียว 7 ลูกจาก 9 ลูกถ้าเป็นไห ข. ก็จะเหลือสีเขียว 3 ลูกจาก 9 ลูก ดังนั้นแบ่งพื้นที่ใหม่ก็กลายเป็นแบบนี้
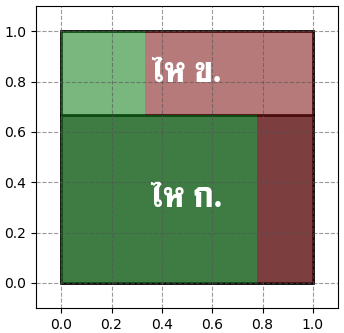
โอกาสที่จะหยิบได้สีเขียวอีกจึงกลายเป็น
สมมุติว่าถ้าหยิบอีกครั้งแล้วยังคงได้สีเขียวอีก คราวนี้
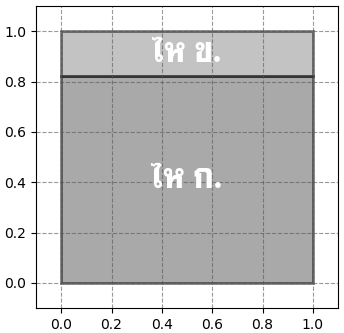
จากตัวอย่างนี้จะเห็นว่าถ้าเราไม่รู้ว่าไหนี้เป็นใบไหนก็ไม่รู้ว่าความน่าจะเป็นที่จะหยิบได้เป็นเท่าไหร่ ก็ต้องมาดูว่าความน่าจะเป็นที่จะเป็นไหใบไหนเป็นเท่าใดด้วย
แต่เมื่อหยิบบอลไปทีนึงแล้วรู้ผลก็จะทำให้เดาได้ง่ายขึ้นว่าไหใบนี้ควรจะเป็นใบไหน และนำความน่าจะเป็นที่ได้มาใหม่นี้ไปคำนวณความน่าจะเป็นในการหยิบครั้งต่อไปอีกที
บทถัดไป >> บทที่ ๔