ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๒: มองความน่าจะเป็นว่าเป็นเหมือนการแบ่งพื้นที่
เขียนเมื่อ 2020/07/25 19:06
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๑
ในบทนี้จะแนะนำพื้นฐานของเรื่องความน่าจะเป็น โดยอาศัยวาดภาพแสดงเปรียบเทียบความน่าจะเป็นว่าเป็นพื้นที่เพื่อให้เห็นภาพ
มองภาพโดยรวมของความน่าจะเป็นจากการโยนเหรียญและทอยลูกเต๋า
เมื่อพูดถึงความน่าจะเป็นแล้วสิ่งที่มักจะนึกถึงเป็นตัวอย่างที่เห็นภาพง่ายๆก็คือเช่นการโยนเหรียญหรือทอยลูกเต๋า
เวลาโยนเหรียญขึ้นไปแล้วดูว่าจะหงายหน้าไหนขึ้น สำหรับเหรียญธรรมดาทั่วไปถ้าไม่ได้ใส่ลูกเล่นพิสดารอะไรลงไป ความน่าจะเป็นที่จะหงายหน้าหัวหรือก้อยก็ควรจะเท่ากัน นั่นคือครึ่งๆ

ในศาสตร์ความน่าจะเป็นโดยทั่วไปแล้วจะถือว่าความน่าจะเป็นของแต่ละเหตุการณ์ที่เป็นไปได้เป็นจำนวนบวกที่มีค่าไม่เกิน 1 และทุกเหตุการณ์รวมกันเป็น 1
ดังนั้นเมื่อบอกว่าโยนเหรียญโอกาสออกหัวก้อยครึ่งๆ หมายความว่าความน่าจะเป็นคือ 1/2 ทั้งคู่
โดยทั่วไปเพื่อให้นึกภาพได้ มักเปรียบเทียบเป็นเหมือนกับการแบ่งพื้นที่ โดยพื้นที่รวมทั้งหมดคือ 1
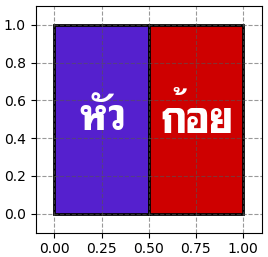
ในทางคณิตศาสตร์มักเขียนแสดงความน่าจะเป็นของเหตุการณ์ต่างๆในลักษณะนี้
วิธีเขียนเป็น
P(เงื่อนไข) = ค่าความน่าจะเป็น แบบนี้เป็นหลักสากลที่ใช้กันทั่วไป บางที่อาจเขียน p()
ตัวพิมพ์เล็ก หรือเขียนเป็น Pr() หรือ Prob() ก็มี แต่ส่วนใหญ่จะเขียนเป็น P() แบบนี้
ในบทความนี้เองก็จะเขียนแบบนี้ตลอดด้วยส่วนกรณีของการทอยลูกเต๋าซึ่งโดยทั่วไปมี 6 หน้า
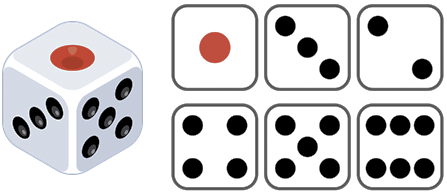
โอกาสออกแต่ละหน้าเท่ากันก็ควรจะเป็นแบบนี้
ถ้าวาดเป็นการแบ่งพื้นที่ดูก็อาจจะเป็นแบบนี้
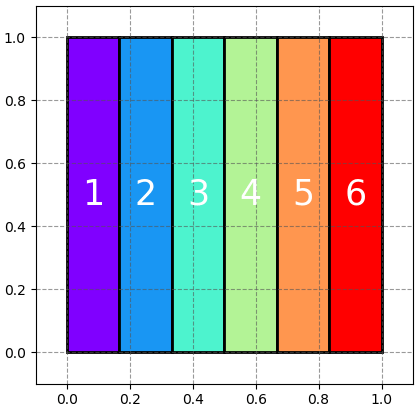
นอกจากนี้ยังอาจพิจารณาเหตุการณ์ต่างๆที่รวมถึงหลายหน้าพร้อมกันเช่น
- ได้เลขคี่: คือได้ 1,3,5
- ได้มากกว่า 3: คือได้ 4,5,6
- ได้ 2 ขึ้นไป: คือได้ 2,3,4,5,6
อาจเขียนสมาชิกของเหตุการณ์ในรูปของเซ็ต เช่น {1,3,5}, {4,5,6}, {2,3,4,5,6} แบบนี้
ความน่าจะเป็นของเหตุการณ์เหล่านี้ก็จะเป็น
ยิ่งไปกว่านั้น บางทีโลกนี้ก็อาจไม่ได้เรียบง่ายแบบนั้น เช่นถ้ามีใครใช้วิธีการอะไรบางอย่างทำให้หน้าเหรียญหน้าหนึ่งมีโอกาสออกมากกว่าอีกหน้า เช่นโอกาสออกหัวเหลือแค่ 2/5 ออกก้อย 3/5
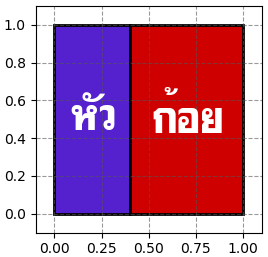
ลูกเต๋าเองก็อาจมีการเล่นตุกติกให้บางหน้ามีโอกาสออกมากว่าหน้าอื่น เช่นความน่าจะเป็นกลายเป็นแบบนี้
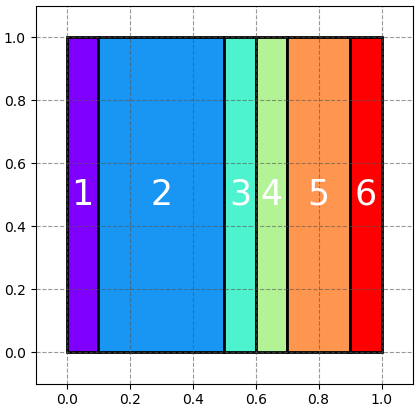
ถ้าเป็นแบบนี้ ความน่าจะเป็นของเหตุการณ์เหล่านี้ก็ต้องเปลี่ยนไป โดยรวมจากพื้นที่ที่แบ่งแบบใหม่นี้
จะเห็นได้ว่าเมื่อเทียบความน่าจะเป็นเป็นการแบ่งพื้นที่แล้วจะช่วยให้นึกภาพได้เข้าใจได้ง่ายขึ้น
ทดลองสุ่มด้วยไพธอน
เพื่อให้เห็นภาพการสุ่ม ลองจำลองการทอยลูกเต๋าได้โดยเขียนโปรแกรม ซึ่งในภาษาไพธอนมีมอดูล random ใช้สำหรับสุ่มค่าตัวเลข
import random
n = 100 # จำนวนลูกเต๋าที่จะโยน
natao = [] # ลิสต์สำหรับเก็บค่าหน้าเต๋าที่ได้
for i in range(n):
natao += [random.randint(1,6)] # ทำการสุ่มแล้วเก็บค่าที่ได้ลงลิสต์
print(natao) # แสดงค่าจะได้ตัวเลขออกมาแบบสุ่มในลักษณะประมาณนี้
[1, 5, 2, 5, 4, 6, 2, 4, 1, 1, 1, 4, 5, 1, 2, 2, 4, 3, 2, 2, 1, 5,
4, 2, 5, 6, 4, 5, 4, 3, 6, 6, 2, 2, 1, 3, 3, 4, 3, 4, 1, 1, 5, 1, 3, 6, 3, 6, 3, 5, 3, 3, 6, 1, 5, 6, 3, 4, 6, 6, 6,
1, 5, 2, 2, 2, 3, 2, 4, 3, 2, 1, 4, 1, 4, 6, 1, 4, 6, 4, 2, 6, 3, 2, 5, 5, 6, 5, 3, 3, 2, 5, 5, 1, 5, 3, 3, 2, 3, 4]
ในการนับจำนวนของแต่ละตัวภายในลิสต์อาจใช้ฟังก์ชัน Counter จากมอดูล collections ซึ่งจะได้จำนวนของแต่ละค่าออกมาโดยเรียงตามลำดับ (สำหรับรายละเอียดวิธีใช้ Counter มีเขียนไว้ใน https://phyblas.hinaboshi.com/20200413 ดูเพิ่มเติมได้)
from collections import Counter
print(Counter(natao))ได้
Counter({3: 19, 2: 18, 1: 16, 5: 16, 4: 16, 6: 15})
ต่อไปลองดูกรณีที่ความน่าจะเป็นของแต่ละตัวเลขไม่เท่ากัน แบบนี้อาจใช้ฟังก์ชัน choice() โดยใส่ลิสต์ของค่าที่ต้องการไปตามสัดส่วนจำนวนที่มีโอกาสออก
import random
from collections import Counter
p = [1,2,2,2,2,3,4,5,5,6] # ลิสต์ที่ใส่เลขเป็นจำนวนตามความน่าจะเป็นที่จะออก
n = 100
natao = []
for i in range(n):
natao += [random.choice(p)] # สุ่มตัวเลขจากในลิสต์
print(natao) # ดูผลที่ได้
print(Counter(natao)) # นับจำนวนจะได้ตัวเลขสุ่มออกมาประมาณนี้
[1, 5, 6, 2, 6, 5, 2, 3, 5, 4, 1, 3, 1, 5, 4, 2, 5, 2, 3, 2, 6, 2, 5, 2, 5, 1, 3, 2, 3, 2, 6, 1, 2, 2, 2, 2, 3, 2,
2, 2, 3, 2, 4, 4, 2, 2, 4, 5, 6, 6, 4, 2, 6, 6, 2, 2, 5, 2, 2, 2, 2, 4, 2, 2, 1, 5, 2, 5, 5, 2, 3, 5, 5, 2, 5, 1, 2,
2, 6, 5, 1, 2, 2, 6, 5, 2, 3, 2, 5, 2, 3, 6, 2, 2, 4, 4, 2, 2, 5, 1]
Counter({2: 42, 5: 19, 6: 11, 3: 10, 1: 9, 4: 9})
Counter({2: 42, 5: 19, 6: 11, 3: 10, 1: 9, 4: 9})
นี่เป็นผลที่ได้จากการลองครั้งหนึ่ง ถ้าลองซ้ำๆหลายครั้งดูผลที่ได้ก็จะได้ต่างกันออกไปไม่เหมือนกัน
ความน่าจะเป็นร่วม
ต่อมาลองพิจารณาความสัมพันธ์ของ 2 เหตุการณ์ขึ้นไปที่อาจเกิดพร้อมกัน
ปกติเมื่อเขียน
P(เหตุการณ์ ก., เหตุการณ์ ข.) แบบนี้ จะหมายถึงความน่าจะเป็นที่จะเกิดเหตุการณ์ ก.
พร้อมกับเหตุการณ์ ข.เช่น สำหรับลูกเต๋าธรรมดาที่มีโอกาสออกทุกหน้าเท่ากัน ความน่าจะเป็นที่จะทอยลูกเต๋าได้มากกว่า 2 แต่น้อยกว่า 5 (ซึ่งก็คือ 3, 4) อาจเขียนได้เป็น
ความน่าจะเป็นที่จะเกิด 2 เหตุการณ์ขึ้นไปพร้อมกันแบบนี้เรียกว่าความน่าจะเป็นร่วม (联合概率, joint probability)
อาจวาดเป็นภาพได้ในลักษณะนี้
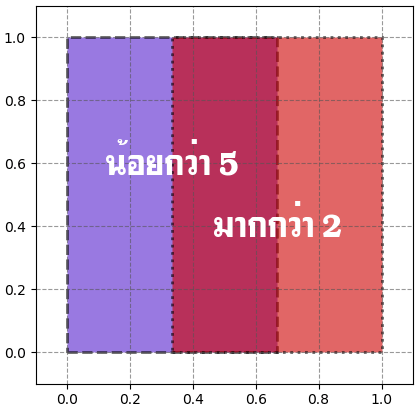
โดยความน่าจะเป็นร่วมก็คือพื้นที่ส่วนที่ซ้อนทับกันนั่นเอง
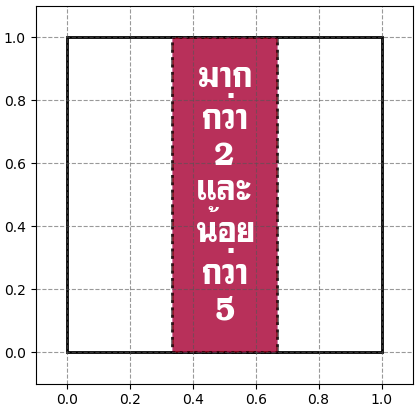
ถ้ามองว่าเหตุการณ์เป็นเหมือนเซ็ต ก็คือการนำเซ็ตมาอินเทอร์เซ็กต์ (相交, intersect) กัน ซึ่งมักเขียนโดยใช้ตัวดำเนินการ ∩ คั่น
ความน่าจะเป็นร่วมจะไม่มากไปกว่าความน่าจะเป็นของเหตุการณ์หนึ่งๆแยกกัน เพราะมีเงื่อนไขมากขึ้น ความน่าจะเป็นก็ต้องลดลง หรืออย่างมากก็เท่าเดิม
เหตุการณ์บางอย่างไม่อาจเกิดขึ้นพร้อมกันได้ เรียกว่าเป็นเหตุการณ์ที่ไม่เกิดร่วมกัน (互斥, mutually exclusive) แบบนี้ความน่าจะเป็นร่วมก็จะเป็น 0 เช่น
ความเป็นอิสระจากกันของเหตุการณ์
หากเหตุการณ์อย่างหนึ่งที่เกิดขึ้นไม่ได้ทำให้ความน่าจะเป็นของอีกเหตุการณ์เปลี่ยนแปลงไปเลย แบบนี้เรียกว่าเป็นอิสระต่อกัน (独立, independent)
ในกรณีนีแบบนี้ ความน่าจะเป็นร่วมของทั้ง 2 เหตุการณ์จะเท่ากับความน่าจะเป็นของทั้ง 2 เหตุการณ์คูณกัน
นั่นคือ ถ้า A และ B เป็นเหตุการณ์ที่เป็นอิสระต่อกัน จะได้ว่า
ตัวอย่างเช่นโยนเหรียญไปด้วย ทอยลูกเต๋าไปด้วย อย่างละอัน ความน่าจะเป็นที่จะได้เหรียญออกหัวกับความน่าจะเป็นที่ทอยลูกเต๋าได้มากกว่า 4 ไม่ได้เกี่ยวข้องอะไรกัน
ดังนั้น
อาจเขียนภาพเป็นการแบ่งพื้นที่แสดงได้ในลักษณะนี้
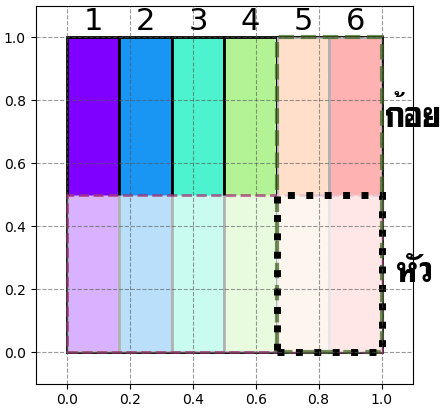
ดูแล้วช่วยให้พอเห็นภาพว่าเหตุการณ์ที่เป็นอิสระจากกันก็เหมือนกับพื้นที่ที่ต่างคนต่างแบ่งอยู่คนละแกนแบบนี้ ในที่นี้แกนตั้งเป็นการโยนเหรียญ แกนนอนเป็นหน้าลูกเต๋า จะเห็นว่าสัดส่วนพื้นที่ที่เหลือได้จากการเอามาคูณกันแบบนั้นเลย
ถ้ามีกี่เหตุการณ์ที่เป็นอิสระต่อกันก็คูณกันไปเท่านั้น เช่นโยนเหรียญ 3 ครั้ง
แต่ถ้าทั้ง 2 เหตุการณ์ไม่ได้เป็นอิสระต่อกันจะไม่สามารถนำมาคูณกันได้แบบนี้ ดังนั้นการคูณนี้จะทำได้ภายใต้เงื่อนไขที่ว่าเหตุการณ์เป็นอิสระต่อกันเท่านั้น
ถ้าหากพบว่า
แบบนี้ก็แสดงว่าเหตุการณ์ A และ B ไม่เป็นอิสระต่อกัน
เช่น พิจารณาความน่าจะเป็นที่ลูกเต๋าจะได้มากกว่า 3 และลูกเต๋าลูกเดียวกันนี้จะได้เลขคู่
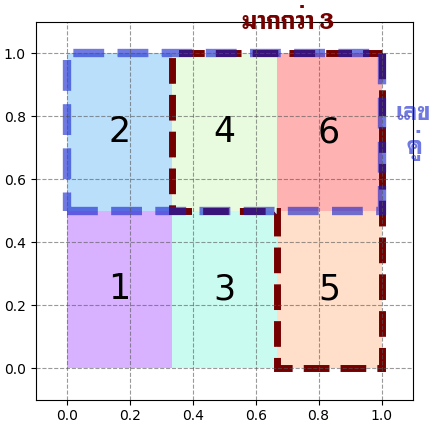
ความน่าจะเป็นแบบมีเงื่อนไข
หากต้องการหาความน่าจะเป็นที่จะเกิดเหตุการณ์หนึ่ง ในขณะที่เกิดอีกเหตุการณ์หนึ่งไปด้วย แบบนี้เรียกว่าความน่าจะเป็นแบบมีเงื่อนไข (条件概率, conditional probability)
ปกติความน่าจะเป็นแบบมีเงื่อนไขจะเขียนในรูปแบบนี้
โดยใช้เครื่องหมาย "|" กั้นแบบนี้ ซึ่งต่างจากกรณีของความน่าจะเป็นร่วมที่จะใช้จุลภาค "," กั้น วิธีการเขียนแบบนี้ใช้เป็นสากล ควรจะทำความเข้าใจความแตกต่างเมื่อเห็นสัญลักษณ์วิธีการเขียน
ความน่าจะเป็นแบบมีเงื่อนไขสามารถคำนวณได้จากความน่าจะเป็นร่วมได้โดย
ถ้าอธิบายเป็นคำพูดก็คือ โอกาสที่จะเกิดเหตุการณ์ A เมื่อเกิดเหตุ B เท่ากับโอกาสที่จะเกิดเหตุการณ์ A และ B พร้อมกัน หารด้วยโอกาสที่จะเกิดเหตุการณ์ B
ยกตัวอย่างเช่น ดูความน่าจะเป็นของการที่ลูกเต๋าที่มีค่าน้อยกว่า 4 จะเป็นเลขคี่ และความน่าจะเป็นที่ลูกเต๋าที่มีค่าน้อยกว่า 4 จะเป็นเลขคู่
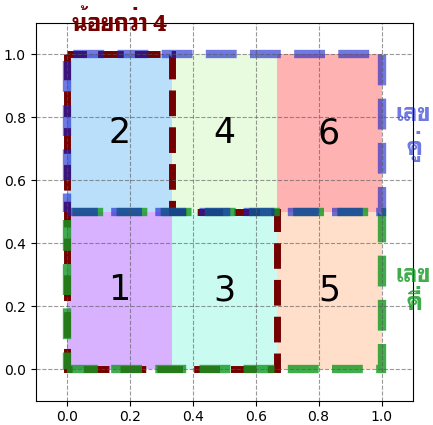
ดูจากขนาดของพื้นที่แล้วก็จะเห็นว่า
ความน่าจะเป็นแบบมีเงื่อนไขได้จากการหารค่าความจะเป็นที่เป็นเงื่อนไข ดังนั้นค่าจึงไม่น้อยไปกว่าความน่าจะเป็นร่วม และความน่าจะเป็นร่วมก็จะไม่มากไปกว่าความน่าจะเป็นของแต่ละเหตุการณ์ ดังนั้นความน่าจะเป็นแบบมีเงื่อนไขก็จะไม่มากไปกว่า 1
ความน่าจะเป็นแบบมีเงื่อนไขอาจจะมีค่ามากขึ้นหรือน้อยลงจากความน่าจะเป็นของเหตุการณ์นั้นเดี่ยวๆโดยไม่มีเงื่อนไขก็ได้ คือ P(A|B) อาจมากหรือน้อยกว่า P(A) และอาจมากหรือน้อยกว่า P(B)
ซึ่งนั่นหมายความว่าการมีเงื่อนไขอาจทำให้ความน่าจะเป็นของเหตุการณ์เพิ่มขึ้นหรือลดลงก็ได้ แล้วแต่เงื่อนไขที่เข้ามา
เช่นนึกถึงเหตุการณ์ที่ว่าเราทอยลูกเต๋าแล้วดูความน่าจะเป็นที่จะได้เลขคู่หรือเลขคี่ แบบนี้ถ้าไม่รู้อะไรเลย ความน่าจะเป็นคือ 1/2 ทั้งคู่
แต่ถ้าก่อนที่จะดูผลที่ออกจริงๆมีคนมาบอกเราว่าหน้าลูกเต๋าได้น้อยกว่า 4 แบบนั้นความน่าจะเป็นที่จะเป็นเลขคี่ก็จะกลายเป็น 2/3 ซึ่งเพิ่มขึ้น และความน่าจะเป็นที่จะเป็นเลขคู่ก็ลดลงกลายเป็น 1/3
สำหรับเหตุการณ์ที่ไม่อาจเกิดพร้อมกันได้ ความน่าจะเป็นร่วมก็เป็น 0 ดังนั้นความน่าจะเป็นแบบมีเงื่อนไขก็จะเป็น 0 ไปด้วย
ความน่าจะเป็นแบบมีเงื่อนไขเมื่อเหตุการณ์เป็นอิสระต่อกัน
ถ้าเหตุการณ์ A และ B เป็นอิสระต่อกัน แบบนั้นแล้วจะได้ว่า
นั่นคือไม่ว่าเหตุการณ์ B จะเกิดขึ้นหรือเปล่าก็ไม่มีผลต่อความน่าจะเป็นของเหตุการณ์ A เพราะเป็นเหตุการณ์ที่เป็นอิสระจากกัน
ยกตัวอย่างเช่นการโยนเหรียญกับทอยลูกเต๋าอย่างละอัน
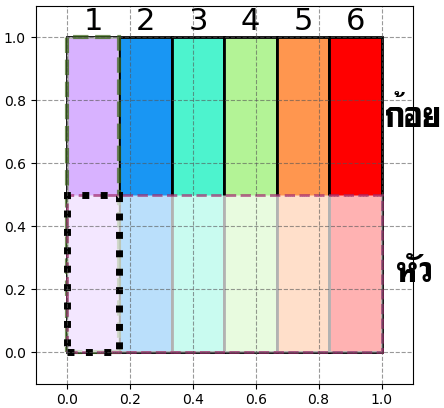
คือลูกเต๋าจะออกหน้าไหนก็ไม่สน ยังไงโอกาสที่เหรียญจะได้หัวก็เป็น 1/2 อยู่ดี นี่คือตัวอย่างของเหตุการณ์ที่ไม่ได้เกี่ยวข้องกับอีกเหตุการณ์
บทถัดไป >> บทที่ ๓