ต่อจาก บทที่ ๗

ในบทนี้จะเข้าสู่เรื่องของความน่าจะเป็นของปริมาณที่เป็นค่าต่อเนื่อง ซึ่งเป็นเนื้อหาที่มีความเป็นนามธรรมเข้าใจยากกว่าปริมาณที่เป็นค่าไม่ต่อเนื่องดังในบทที่ผ่านมา




อะไรคือต่อเนื่องกับไม่ต่อเนื่อง

ในบทที่ผ่านมาเป็นการพูดถึงปริมาณที่นับได้แน่นอน มีจุดชัดเจนว่าจะมีค่าเท่าใดได้บ้าง และพิจารณาแค่ค่าที่มีอยู่และความเป็นไปได้ของค่านั้น เช่นแต้มลูกเต๋า จำนวนไอเท็มที่ดร็อปได้

ปริมาณแบบนั้นเรียกว่าเป็นค่าไม่ต่อเนื่อง (离散, discrete)

ค่าไม่ต่อเนื่องมีจำนวนแน่นอน ส่วนใหญ่จะเป็นจำนวนเต็ม แต่ก็ไม่จำเป็น เช่นถ้าพูดถึงคะแนนสอบซึ่งมีการให้ 0.5 ด้วย แบบนั้นคะแนนสอบก็ถือเป็นค่าไม่ต่อเนื่องได้

แต่ปริมาณทั่วไปหลายสิ่งที่พบในธรรมชาติไม่ได้เป็นเช่นนั้น เช่นเวลา (วินาที) น้ำหนัก (กก.) ส่วนสูง (ซม.) ระยะทาง (กม.) ฯลฯ ค่าอาจเป็นเท่าไหร่ก็ได้ ไม่มีค่าที่เรียกว่าพอดีเป๊ะเท่านั้นจริงๆ

เช่นถ้าบอกว่าหนัก 50 กิโลกรัม ปกติแล้วก็ไม่ได้หมายความว่าหนัก 50 เป๊ะ แค่หนักประมาณเท่านั้น ถ้าไปวัดให้ละเอียดอาจจะเป็น 50.01234567 มีทศนิยมค่าเล็กๆซึ่งถูกปักทิ้งอยู่อีกมากมายไม่สิ้นสุด

ปริมาณแบบนี้เรียกว่าเป็นค่าต่อเนื่อง (连续, continuous)

อาจนึกภาพประมาณนี้



นอกจากนี้แล้ว ตัวค่าความน่าจะเป็นเองก็ถือเป็นปริมาณต่อเนื่องเช่นกัน เพราะมีค่าเท่าไหร่ก็ได้ตั้งแต่ 0 ถึง 1 และเรื่องของ "ความน่าจะเป็นของความน่าจะเป็น" ก็เป็นเนื้อหาสำคัญอย่างหนึ่งที่น่ากล่าวถึงเช่นกัน

เมื่อมาคิดเรื่องของความน่าจะเป็นสำหรับค่าต่อเนื่อง จะมีวิธีคิดที่ต่าไปต่างค่าแบบไม่ต่อเนื่อง แม้ส่วนใหญ่จะเทียบเคียงกันได้ แต่มักจะยากกว่า เป็นนามธรรมมากกว่า ต้องใช้จินตนาการเพิ่มเติมมากกว่า




ฟังก์ชันความหนาแน่นของความน่าจะเป็น

เมื่อพูดถึงเรื่องความน่าจะเป็นของค่าต่อเนื่อง ประเด็นน่าสนใจที่มักจะพูดถึงก็คือการที่ค่าความน่าจะเป็นของจุดใดๆจะเป็น 0 เสมอ

สาเหตุเนื่องจากว่าค่าต่อเนื่องไม่มีค่าใดๆที่เป็นค่าเป๊ะๆ ดังนั้นถ้าคิดจะหาค่าความน่าจะเป็นของค่าใดค่าหนึ่งที่แน่นอน ก็ย่อมจะได้ 0 เสมอ


แต่ความน่าจะเป็นเป็นสิ่งที่ต้องรวมกันหมดแล้วได้ 1 ถ้ามีแต่ 0 บวกกันแล้วจะกลายเป็น 1 ได้อย่างไร? นี่เป็นความจริงอย่างหนึ่งที่ชวนให้สับสน แต่โลกนี้ก็เต็มไปด้วยอะไรที่เหนือสามัญสำนึกแบบนี้อยู่มากมายจริงๆ

เมื่อค่าไม่ได้เป็นจุดๆที่ไม่ต่อเนื่องที่จะแยกได้ชัดแบบนี้จึงไม่มีความหมายอะไรที่จะหาความน่าจะเป็นของค่านั้นพอดี แต่จะพิจารณาเป็นช่วงๆแทน เช่น P(50 กก. ≤ น้ำหนัก ≤ 55 กก.) หรือ P(160 ซม. ≤ สูง ≤ 165 ซม.) แบบนี้จึงจะมีค่า

เมื่อพูดถึงการแจกแจงความน่าจะเป็นของค่าแบบต่อเนื่อง ความน่าจะเป็นในแต่ละช่วงมักจะคำนวณโดยพิจารณาจากฟังก์ชันความหนาแน่นของความน่าจะเป็น (概率密度函数, probability density function) ซึ่งเป็นตัวบอกว่าในบริเวณนั้นมีความน่าจะเป็นเท่าใด

ให้ f_X(x) เป็นฟังก์ชันความหนาแน่นของความน่าจะเป็น จะได้ว่าความน่าจะเป็นในช่วงระหว่าง a ถึง b เป็นปริพันธ์จำกัดเขต (definite integral) ในช่วง a ถึง b


หากวาดกราฟของ f_X(x) แล้ว ความน่าจะเป็นภายในช่วงก็จะเท่ากับพื้นที่ใต้กราฟในช่วงนั้น



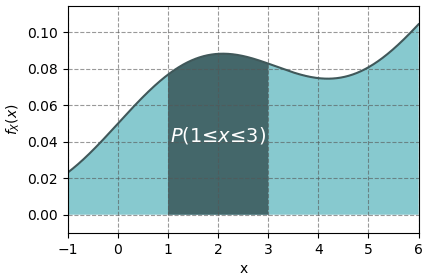
ความน่าจะเป็นรวมทั้งหมดต้องได้ 1 ดังนั้นผลรวมของพื้นที่ไต้กราฟทั้งหมดตั้งแต่ -∞ ไปจนถึง ∞ ก็จะต้องเป็น 1 เสมอ





การแจกแจงเอกรูปต่อเนื่อง

เพื่อเป็นตัวอย่างวิธีการใช้ฟังก์ชันการแจกแจงความหนาแน่นเพื่อคำนวณความน่าจะเป็น เริ่มจากขอยกตัวอย่างรูปแบบการแจกแจงความหนาแน่นความน่าจะเป็นที่เข้าใจง่ายที่สุด นั่นก็คือ การแจกแจงเอกรูปต่อเนื่อง (连续型均勻分布, continuous uniform distribution)

คำว่า "เอกรูป" อาจฟังดูไม่คุ้น แต่ก็แปลได้ตรงตัว "เอก" คือ 1 "รูป" ก็คือรูป จึงหมายถึงเป็นการแจงที่มีอยู่รูปแบบเดียวตลอดทั้งหมดในขอบเขตช่วงหนึ่ง

ถ้าฟังก์ชัน f_X แจกแจงแบบเอกรูปต่อเนื่อง จะได้ว่า


ที่มีตัวหาร b-a อยู่ก็เพื่อให้พื้นที่ใต้กราฟรวมได้เท่ากับ 1

เมื่อวาดกราฟก็จะออกมาเป็นลักษณะที่ราบสูงแบบนี้



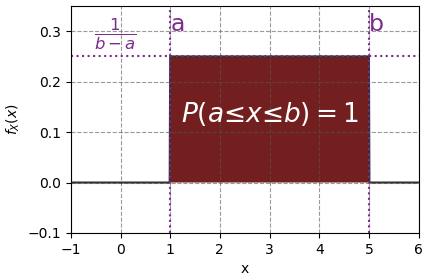
โดยทั่วไปการแจกแจงจะอยู่แค่ในช่วงใดช่วงหนึ่งที่แน่นอนเท่านั้น เพราะพื้นที่ใต้กราฟต้องรวมแล้วได้ค่าจำกัดเท่ากับ 1 ดังนั้นความสูงของที่ราบก็จะแปรผกผันกับความกว้างของที่ราบ

ในที่นี้ใช้เครื่องหมายน้อยกว่าหรือเท่ากับ (≤) ก็จริง แต่จริงๆจะใช้น้อยกว่า (<) ก็ไม่ต่างกัน เพราะไม่มีค่าที่จุดนั้นพอดีอยู่แล้ว

การแจกแจงแบบนี้พบได้ในชีวิตประจำวันในหลายกรณีด้วย ยกตัวอย่างเช่น ลองนึกถึงรูเล็ต (roulette) อุปกรณ์พนันที่โยนบอลลงไปในวงกลม ดูว่าบอลตกช่องไหน



เพียงแต่ว่ารูเล็ตโดยทั่วไปจะมีการแบ่งเป็นช่องชัดเจน เช่นในรูปนี้เป็นตัวเลขตั้งแต่ 0 ถึง 36 ซึ่งถ้าเป็นแบบนี้ก็ถือเป็นการแจกแจงเอกรูปเหมือนกัน แต่ค่าเป็นค่าไม่ต่อเนื่องจึงกลายเป็นการแจกแจงเอกรูปแบบไม่ต่อเนื่อง (离散型均匀分布, discrete uniform distribution)

ดังนั้นให้นึกถึงรูเล็ตที่ไม่มีช่องกั้น เช่นสมมุติว่าเอาบอลไปโยนลงในหมวกแบบที่ผีดิบจีน เจียงซือ (僵尸jiāng shī) ชอบใส่ ก็ได้


เจียงซือ! (ที่มาของภาพ)

เมื่อโยนบอลลงไปในหมวกของเจียงซือ บอลจะไปตกอยู่ตรงตำแหน่งมุมเท่าไหร่ก็มีโอกาสพอๆกัน ดังนั้นการแจกแจงความน่าจะเป็นจึงได้เป็น


ในไพธอนมีฟังก์ชัน uniform() ในมอดูล random เอาไว้ใช้สุ่มค่าต่อเนื่องโดยมีความน่าจะเป็นสม่ำเสมอภายในช่วงที่ต้องการได้

สมมุติว่าโยนบอล 100 ครั้ง จากนั้นแสดงผลด้วย matplotlib ดู

import matplotlib.pyplot as plt
import random
  
mum = []
for i in range(100):
    # สุ่มมุมตั้งแต่ 0 ถึง 360
    mum += [random.uniform(0,360)]

# วาดกราฟ
plt.xlim(-10,370) # กำหนดขอบเขตแกน x
plt.yticks([]) # ไม่ต้องแสดงแกน y
for i in range(100):
    # วาดเส้นตามตำแหน่งที่สุ่มได้
    plt.axvline(mum[i],alpha=0.2)
plt.show()

จะได้กราฟแบบนี้ออกมา ซึ่งมีการกระจายของค่าอย่างสม่ำเสมอในช่วง 0 ถึง 360 อาจมีบางส่วนหนาแน่นบ้างเพราะมีความไม่แน่นอน แต่โดยรวมแล้วกระจายสม่ำเสมอ






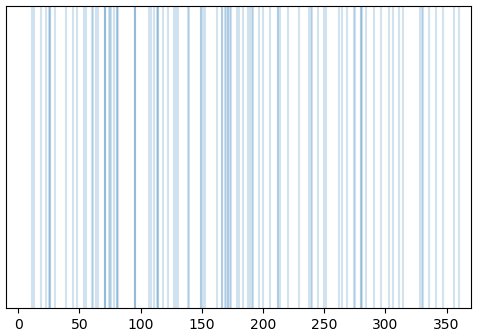
ค่าคาดหมาย

เช่นเดียวกับในกรณีของค่าไม่ต่อเนื่อง ค่าคาดหมายเป็นคุณสมบัติอย่างหนึ่งที่สำคัญสำหรับการแจกแจงของค่าแบบต่อเนื่องเช่นกัน

ค่าคาดหมายของตัวแปรสุ่มที่เป็นค่าต่อเนื่องคำนวณได้จากปริพันธ์ของค่าตั้งแต่ -∞ ถึง ∞ คูณด้วยฟังก์ชันความหนาแน่น


โดยภาพรวมแล้วก็คล้ายๆกับกรณีค่าไม่ต่อเนื่อง แต่เปลี่ยนจากผลรวม (Σ) เป็นปริพันธ์ (∫)

ตัวอย่างเช่น สมมุติว่ามีฟังก์ชันความหนาแน่นความน่าจะเป็นเป็นแบบเอกรูปดังนี้




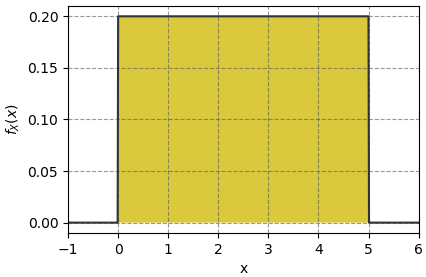
ค่าคาดหมายคำนวณได้ว่า


สำหรับฟังก์ชันเอกรูปแบบนี้แน่นอนว่าค่าคาดหมายก็คือที่ใจกลางที่ราบสูง

ส่วนค่าคาดหมายของ g(X) ซึ่งเป็นฟังก์ชันของ X ก็สามารถคำนวณจากฟังก์ชันความหนาแน่นความน่าจะเป็นของ X ได้โดย


ตัวอย่าง สมมุติว่าฟังก์ชันความหนาแน่นความน่าจะเป็นเป็นดังนี้




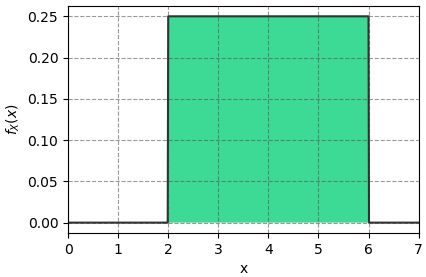
หากต้องการคำนวณค่าคาดหมายของ X² จะได้ว่า





ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน

ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานมีวิธีคิดที่เหมือนกับกรณีค่าไม่ต่อเนื่อง นั่นคือ


เพียงแต่เวลาคำนวณจะใช้การหาปริพันธ์

ตัวอย่าง มีฟังก์ชันการแจกแจงความหนาแน่นดังนี้




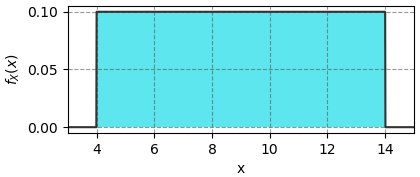
เริ่มจากคำนวณหาค่าคาดหมาย E(X)


คำนวณความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน





ฟังก์ชันแจกแจงความหนาแน่นสะสม

ปริมาณอีกอย่างที่มักใช้อธิบายการแจกแจงความหนาแน่นของค่าต่อเนื่องก็คือ ฟังก์ชันแจกแจงสะสม (累积分布函数, cumulative distribution function) ซึ่งเป็นค่าที่ได้จากการหาปริพันธ์ของฟังก์ชันแจกแจงความน่าจะเป็นตั้งแต่ -∞ ไปจนถึงค่านั้น

ฟังก์ชันแจกแจงสะสม F_X ที่ตำแหน่ง a คำนวณได้โดย


ในขณะที่ฟังก์ชันความหนาแน่นความน่าจะเป็นมักใช้เป็น f เล็ก ฟังก์ชันแจกแจงสะสมจะใช้ F ใหญ่

ค่า F_X(a) แสดงถึงความน่าจะเป็นรวมของค่าตั้งแต่ -∞ จนถึง a


ดังนั้น


และความน่าจะเป็นของช่วงตั้งแต่ a ถึง b ก็คือ


ตัวอย่างเช่น ให้


ดังนั้นจะได้ว่า







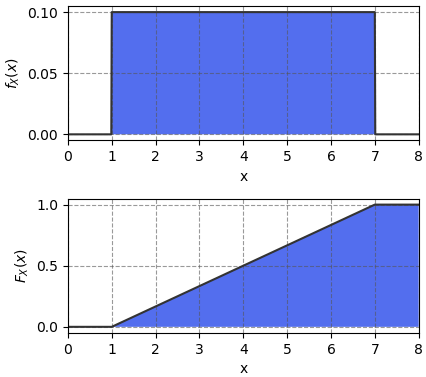
การหาฟังก์ชันความหนาแน่นของความน่าจะเป็นจากฟังก์ชันแจกแจงความหนาแน่นสะสม

เมื่อ F_X เป็นปริพันธ์ของ f_X ดังนั้น f_X ก็เป็นอนุพันธ์ของ F_X


ดังนั้นเมื่อรู้ฟังก์ชันแจกแจงความหนาแน่นสะสม ก็เอามาหาอนุพันธ์เพื่อจะหาฟังก์ชันความหนาแน่นของความน่าจะเป็นได้

ตัวอย่างเช่น ถ้าฟังก์ชันแจกแจงความหนาแน่นสะสมเป็นแบบนี้


จะได้ว่าฟังก์ชันความหนาแน่นของความน่าเป็นคือ


หากวาดกราฟดูก็จะได้แบบนี้





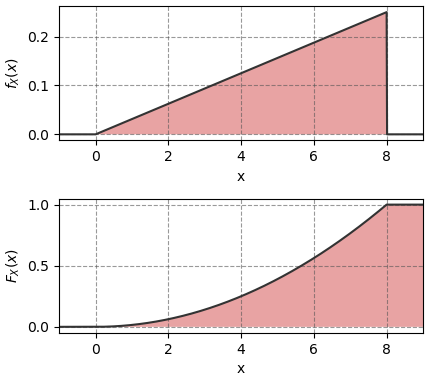
บทถัดไป >> บทที่ ๙

~ 自我介绍 ~

目录

从日本来的名言

python 模块 -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 机器学习 -- 神经网络

javascript

蒙古语

语言学

maya

概率论

与日本相关的日记

与中国相关的日记 -- 与北京相关的日记 -- 与香港相关的日记 -- 与澳门相关的日记

与台湾相关的日记

与北欧相关的日记

与其他国家相关的日记

qiita

其他日志

按类别分日志

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --MATLAB --SQL --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม --สเตเบิลดิฟฟิวชัน ---comfyui -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ -ซางะ -นางาซากิ -คุมาโมโตะ -โออิตะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ -ออสเตรเลีย ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม เรื่องแต่ง บันทึก

　 查看日志

　 最近

　 推荐日志

各月日志

找更早以前的日志

ไทย

日本語

中文