ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๗: การแจกแจงปัวซง
เขียนเมื่อ 2020/07/25 19:11
แก้ไขล่าสุด 2022/07/10 21:01
ต่อจาก บทที่ ๖
ในบทนี้จะยกตัวอย่างการแจกแจงอีกแบบที่พบได้บ่อย นั่นคือการแจกแจงปัวซง
โยนลูกเต๋า n ครั้ง จะออกหน้าหนึ่งกี่ครั้ง?
ลองคิดถึงสถานการณ์ที่มีการสุ่มความน่าจะเป็นสม่ำเสมอกันตลอด เช่นกรณีลูกเต๋าซึ่งมีโอกาสออก 6 หน้าเท่ากัน
งั้นถ้าหากเราทอยลูกเต๋า n ครั้ง จะออกหน้าไหนกี่ครั้ง? แน่นอนว่าโอกาสเท่ากันก็ควรจะได้หน้าละ n/6 เป็นธรรมดา
แต่ว่าในการลองจริงๆก็อย่างที่รู้กันว่าการสุ่มมีโอกาสได้จำนวนครั้งเท่าไหร่ก็ได้ โอกาสได้ n/6 ครั้งมีเยอะสุดก็จริง แต่ก็อาจได้จำนวนอื่น ซึ่งมีโอกาสน้อยกว่าลดหลั่นลงไป
หากพิจารณาการแจกแจงของจำนวนครั้งที่จะลูกเต๋าหน้าใดหน้าหนึ่ง การแจกแจงนั้นจะเป็น การแจกแจงปัวซง (泊松分布, Poisson distribution)
ก่อนอื่นเริ่มจากทดลองจริงๆดู สมมุติว่าทอยลูกเต๋าทั้งหมด 60 ลูกแล้วสนแค่ว่าทอยได้ 1 กี่ครั้ง ลองทำแบบนี้่ซ้ำกันสักหมื่นครั้ง ผลที่ได้จะเป็นเท่าไหร่กี่ครั้ง?
ลองเขียนโดยใช้ฟังก์ชัน Counter() ของมอดูล collections เป็นตัวนับดู
import random
from collections import Counter
kk = [] # ลิสต์เก็บจำนวนลูกเต๋าที่ทอยได้ 1 ในแต่ละครั้ง
for i in range(10000):
k = 0
# ทอยลูกเต๋า 60 ลูก
for j in range(60):
# สุ่มหน้าเต๋า
natao = random.randint(1,6)
# ถ้าได้ 1 ก็บวกเพิ่ม
if(natao==1):
k += 1
kk += [k]ได้
Counter({10: 1388, 9: 1303, 11: 1206, 8: 1170, 12: 1036, 7: 903, 13: 734, 6: 554, 14: 502, 5: 313, 15: 304, 16: 191, 4: 147, 17: 113, 3: 46, 18: 43, 19: 21, 20: 12, 2: 7, 21: 3, 1: 2, 22: 1, 23: 1})จะเห็นว่าที่เจอเยอะที่สุดก็คือแถวๆ 10 ลูก ซึ่งก็เป็นไปตามที่คาด ถ้าให้ทายว่าลูกเต๋า 60 ลูกจะออกแต้ม 1 สักกี่หน้าก็ย่อมต้องเป็น 10 โอกาสเป็นไปได้มากสุดอยู่แล้ว
นำมาวาดแผนภูมิแท่งแสดงการแจกแจงจะได้แบบนี้
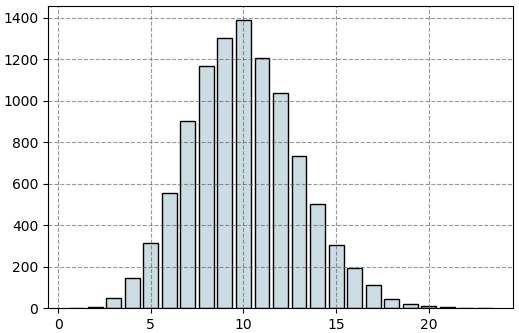
ผลที่ได้ในลักษณะนี้นี่คือการแจกแจงปัวซง
ที่มาของการแจกแจงปัวซง
ต่อมาลองพยายามหาดูว่าการแจกแจงแบบนี้จะอธิบายเป็นสมการได้อย่างไร
ที่จริงแล้วการแจกแจงปังซงก็คือการแจกแจงทวินามในกรณีที่ทำซ้ำเป็นอนันต์ครั้งนั่นเอง
การแจกแจงทวินามคือการแจกแจงของความน่าจะเป็นที่จะทำสำเร็จ k ครั้งจากการทดลองที่มีความน่าจะเป็น p ทั้งหมด n ครั้ง ซึ่งจะได้การแจกแจงความน่าจะเป็นเป็นดังนี้
...(8.1)
ค่าคาดหมายของการแจกแจงทวินามคือผลคูณระหว่างจำนวนครั้งที่ลองกับความน่าจะเป็นที่จะสำเร็จ
เมื่อคิดถึงเหตุการณ์ที่มีโอกาสเกิดขึ้นเท่าๆกันทั้งหมดจำนวนเยอะมาก n→∞ ความน่าจะเป็นของแต่ละเหตุการณ์ก็จะเป็นค่าเล็กมากเข้าใกล้ 0 ด้วย p→0
อย่างไรก็ตาม ในที่นี้ค่าคาดหมาย E(k) ซึ่งเป็นผลคูณระหว่าง n กับ p จะสามารถเป็นจำนวนที่มีค่าคงตัวได้ ซึ่งจะเป็นค่าที่บอกถึงความถี่ของการที่จะเกิดเหตุการณ์ที่สำเร็จนั้นขึ้น
แทนค่าคาดหมายนี้ด้วย λ จะได้ว่า
จากนั้นแทนค่า p ในสมการ (8.1) จะได้ว่า
ตรงนี้ถ้าหาก n เป็นจำนวนที่มากเข้าใกล้อนันต์จะได้ว่า
ดังนั้น
และจากนิยามของค่า e
จะได้ว่า
และเมื่อ n เป็นจำนวนมากๆ (n-k)/n ก็จะเข้าใกล้ 1 ดังนั้นจึงได้ว่า
และนี่ก็คือรูปทั่วไปของการแจกแจงปัวซง แสดงความน่าจะเป็นที่เหตุการณ์ที่มีค่าความคาดหมายเป็น λ จะเกิดขึ้นสำเร็จ k ครั้ง
เช่นในกรณีทอยลูกเต๋าถ้าโยน 6 ครั้งจะมีโอกาสได้แต่ละหน้าเท่ากันเป็น 1/6 ดังนั้นหากลองคิดกรณีที่โยน 60 ครั้งแล้ว λ=10
เขียนโปรแกรมให้คำนวณตามสมการนี้แสดงการแจกแจงในกรณีของลูกเต๋าได้ดังนี้
import math
λ = 10 # ค่าคาดหมายของเหตุการณ์
pk = [] # ลิสต์เก็บความน่าจะเป็นที่จะได้ k รอบ
for k in range(30+1):
pk += [(λ**k)*math.exp(-λ)/math.factorial(k)]
print(pk)ได้
[4.5399929762484854e-05, 0.00045399929762484856, 0.0022699964881242427, 0.007566654960414142, 0.018916637401035354, 0.03783327480207071, 0.06305545800345118, 0.09007922571921599, 0.11259903214901998, 0.1251100357211333, 0.1251100357211333, 0.11373639611012118, 0.09478033009176766, 0.07290794622443666, 0.05207710444602619, 0.03471806963068413, 0.021698793519177577, 0.012763996187751515, 0.007091108993195286, 0.0037321626279975192, 0.0018660813139987594, 0.0008886101495232189, 0.00040391370432873584, 0.00017561465405597208, 7.317277252332172e-05, 2.9269109009328688e-05, 1.125734961897257e-05, 4.169388747767619e-06, 1.4890674099170067e-06, 5.134715206610368e-07, 1.7115717355367894e-07]ซึ่งวาดเป็นกราฟได้แบบนี้
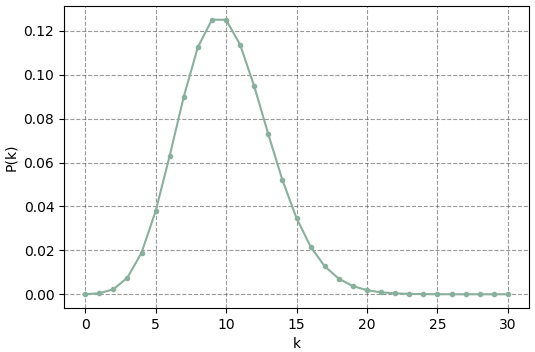
ลักษณะการแจกแจงเป็นไปตามการทดลองสุ่มจริงในตัวอย่างที่แล้ว
หากลองวาดกราฟแสดงการแจกแจงที่ค่า λ ต่างกันตั้งแต่ 1 ไปจนถึง 30 จะได้
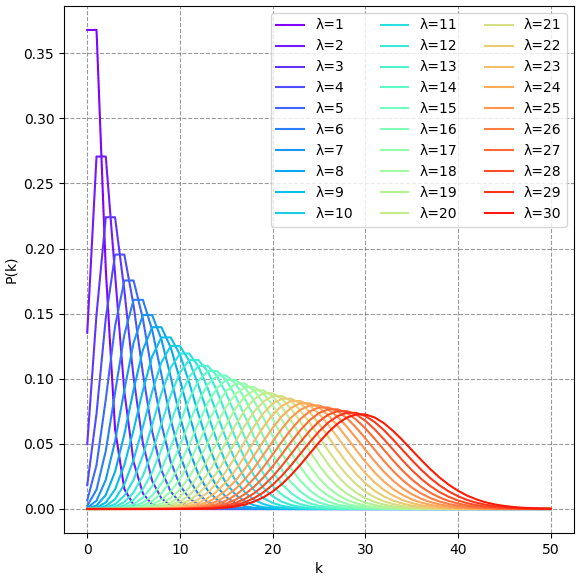
ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานของการแจกแจงปัวซง
การแจกแจงปัวซงนั้นนอกจากค่าคาดหมายจะเป็น λ แล้ว ความแปรปรวนก็เท่ากับ λ ด้วย
วิธีพิสูจน์
ตัวอย่างเพิ่มเติม
ตัวอย่างประโยชน์ของการทำความเข้าใจการแจกแจงปัวซงอย่างหนึ่งที่เจอบ่อยก็คือ เช่นวิเคราะห์จำนวนคนเข้าสถานที่ในช่วงเวลาหนึ่ง
สมมุติเหตุการณ์ว่ามีโรงละครแห่งหนึ่งขายตั๋วการแสดงได้ทั้งหมด 450 ใบ ดังนั้นจึงคาดได้ว่าจะมีคนมาดูทั้งหมด 450 คน แต่การแสดงจัดทั้งหมด 9 รอบ แล้วตั๋วที่ซื้ออาจจะใช้เพื่อเข้าดูรอบไหนก็ได้ ดังนั้นบางรอบอาจมีคนเยอะหรือคนน้อยก็ได้ งั้นในกรณีแบบนี้ควรจะเตรียมที่นั่งไว้สักกี่ที่เพื่อจะให้เพียงพอสำหรับแต่ละรอบ
สำหรับกรณีนี้แน่นอนว่าจำนวนคนในเฉลี่ยแต่ละรอบคือ 50 แต่ก็ต้องมีบางรอบที่คนเข้ามามากหรือน้อยกว่านั้น ถ้าเตรียมไว้แค่ 50 ที่ย่อมจะไม่พอ
ถ้าคิดว่าโอกาสที่คนจะเข้ามาดูแต่ละรอบนั้นมากพอๆกันแล้ว การแจกแจงความน่าจะเป็นของจำนวนคนเข้าชมในแต่ละรอบก็จะเป็นการแจกแจงปัวซง
โดย λ เป็นค่าคาดหมาย (หรือก็คือจำนวนโดยเฉลี่ย) ที่น่าจะในแต่ละรอบ กรณีนี้ λ = 450/9 = 50
ลองวาดกราฟแสดงค่าฟังก์ชันการแจกแจงปัวซงดูก็จะออกมาในลักษณะนี้
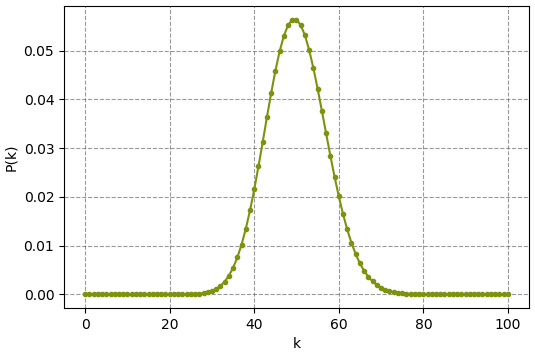
ซึ่งจากกราฟจะพอเห็นได้ว่าส่วนใหญ่ก็จะอยู่ที่ 50 แต่พอสูงถึง 70 ก็เริ่มแทบจะเป็นไปไม่ได้แล้ว
ผลรวมของความน่าจะเป็นในแต่ละค่า k ตั้งแต่ 0 ไปจนถึง k จะแสดงถึงค่าความน่าจะเป็นที่จะมีจำนวนคนไม่เกิน k ดังนั้น
อาจลองเขียนโปรแกรมคำนวณฟังก์ชันการแจกแจงปัวซงแล้วใช้เพื่อคำนวณความน่าจะเป็นสะสมของค่าในช่วง 70-80 ดูได้ดังนี้
import math
λ = 50 # ค่าคาดหมายของเหตุการณ์
pk = [] # ลิสต์เก็บความน่าจะเป็นที่จะได้ k รอบ
for k in range(100+1):
pk += [(λ**k)*math.exp(-λ)/math.factorial(k)]
for k in range(70,80+1):
print('ความน่าจะเป็นที่คนจะเกิน %d ='%k,1-sum(pk[:k+1]))ได้
ความน่าจะเป็นที่คนจะเกิน 70 = 0.0029707355180791373
ความน่าจะเป็นที่คนจะเกิน 71 = 0.0020102676766792227
ความน่าจะเป็นที่คนจะเกิน 72 = 0.0013432761201515042
ความน่าจะเป็นที่คนจะเกิน 73 = 0.000886432588283248
ความน่าจะเป็นที่คนจะเกิน 74 = 0.0005777545262101169
ความน่าจะเป็นที่คนจะเกิน 75 = 0.0003719691514946222
ความน่าจะเป็นที่คนจะเกิน 76 = 0.00023658403655024696
ความน่าจะเป็นที่คนจะเกิน 77 = 0.0001486716242486974
ความน่าจะเป็นที่คนจะเกิน 78 = 9.231751379901176e-05
ความน่าจะเป็นที่คนจะเกิน 79 = 5.6650355286569365e-05
ความน่าจะเป็นที่คนจะเกิน 80 = 3.4358381216237355e-05จากผลการคำนวณก็จะเห็นได้ว่าโอกาสที่คนจะเกิน 70 คนมีแค่ 0.3% เท่านั้น ดังนั้นเตรียมแค่ 70 ที่ก็อาจจะพอ แต่ถ้าต้องการให้แน่นอนกว่านี้อาจเตรียมมากกว่านี้เพื่อให้ความน่าจะเป็นที่จะคนเกินมาลดลง ต้องการความมั่นใจแค่ไหนก็ดูจากผลที่คำนวณนี้ได้
คราวนี้ลองเขียนโปรแกรมเพื่อจำลองสถานการณ์โดยสุ่มดูสักหมื่นครั้ง
import random
from collections import Counter
kk = []
for i in range(10000):
k = 0
# ลูกค้า 900
for j in range(450):
# สุ่มว่าจะเข้าชมการแสดงรอบไหน
h = random.randint(1,9)
# ถ้าได้ 1 ก็บวกเพิ่ม
if(h==1):
k += 1
kk += [k]
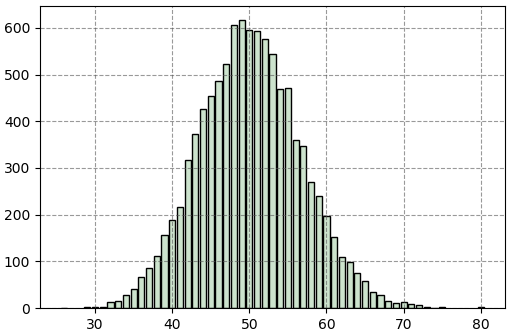
print(Counter(kk))ได้
Counter({49: 616, 48: 606, 50: 596, 51: 593, 52: 577, 53: 543, 47: 522, 46: 487, 55: 472, 54: 468, 45: 453, 44: 426, 43: 373, 56: 359, 57: 346, 42: 318, 58: 270, 59: 239, 41: 216, 60: 197, 40: 189, 39: 157, 61: 152, 38: 112, 62: 110, 63: 98, 37: 85, 64: 75, 36: 66, 65: 57, 35: 40, 66: 35, 67: 27, 34: 27, 33: 15, 68: 14, 70: 13, 32: 13, 69: 10, 71: 8, 72: 6, 73: 2, 29: 2, 30: 2, 80: 2, 31: 2, 75: 2, 26: 1, 74: 1})ผลการแจกแจงออกมาในลักษณะใกล้เคียงกับกราฟที่ได้จากการคำนวณ
บทถัดไป >> บทที่ ๘