ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๖: การแจกแจงแบบเรขาคณิตและการแจกแจงทวินามเชิงลบ
เขียนเมื่อ 2020/07/25 19:10
แก้ไขล่าสุด 2023/08/26 13:16
ต่อจาก บทที่ ๕
ในบทที่แล้วได้กล่าวถึงการแจกแจงทวินามไปแล้ว สำหรับบทนี้จะเป็นเรื่องการทดลองแบบแบร์นุลลี ซึ่งนำไปสู่การแจกแจงแบบเรขาคณิตกับการแจกแจงทวินามเชิงลบ ซึ่งเป็นเรื่องที่ต่อยอดมาจากการแจกแจงทวินาม
การทดลองแบบแบร์นุลลี
การแจกแจงทวินามในกรณีที่ n=1 ซึ่งหมายถึงทำการทดลองเพียงครั้งเดียว จะเป็นกรณีพิเศษที่เรียกว่าการแจกแจงแบร์นุลลี (伯努利分布, Bernoulli distribution)
ค่า k ต้องไม่เกิน n ในที่นี้เมื่อ n เป็น 1 ดังนั้น k เป็นได้แค่ 0 หรือ 1 เท่านั้น
ซึ่งอธิบายถึงกรณีที่ทดลองทำอะไรสักอย่างแล้วมีผลลัพธ์อยู่แค่ ๒ อย่างคือสำเร็จกับล้มเหลว โดยมีความน่าจะเป็นที่จะสำเร็จเป็น p และความน่าจะเป็นที่จะล้มเหลวก็จะเป็น 1-p
การทดลองแบบนี้เรียกว่า การทดลองแบบแบร์นุลลี (伯努利试验, Bernoulli trial)
จำนวนครั้งที่โยนเหรียญกว่าจะออกหัวสักครั้ง
หากทำการทดลองแบบแบร์นุลลีซ้ำๆกันหลายครั้ง ความน่าจะเป็นของจำนวนครั้งที่จะต้องทำเพื่อให้สำเร็จสักครั้งหนึ่งจะมีการแจกแจงเป็นลักษณะที่เรียกว่า การแจกแจงแบบเรขาคณิต (几何分布, geometric distribution)
การแจกแจงแบบเรขาคณิตเป็นฟังก์ชันที่บอกว่าหากทำการทดลองที่มีความน่าจะเป็นที่จะสำเร็จเป็น p จะต้องทำไปกี่ครั้งจึงจะสำเร็จสักครั้ง
ลองเริ่มจากคิดถึงกรณีง่ายๆเช่นโยนเหรียญหัวก้อย โอกาสได้หัวเป็น 0.5
เมื่อโยนเหรียญครั้งแรก ความน่าจะเป็นที่จะได้หัวเป็น 0.5 ครั้งอยู่แล้ว ดังนั้นความน่าจะเป็นที่จะโยน 1 ครั้งแล้วสำเร็จเลยก็จะเป็น 0.5 และมีความน่าจะเป็นที่จะล้มเหลวแล้วต้องโยนครั้งที่ 2 ต่อเป็น 0.5
ถ้าโยนครั้งที่ 2 ความน่าจะเป็นที่จะได้หัวก็เป็น 0.5 อีกเช่นกัน ดังนั้นความน่าจะเป็นที่จะสำเร็จในขั้นนี้ก็เป็น 0.5 คูณกับ 0.5 เป็น 0.25 ส่วนความน่าจะเป็นที่จะล้มเหลวตรงนี้ก็เป็น 0.25 เช่นกัน
ดังนั้นจะเห็นแนวโน้มว่าจะเป็นอย่างไรต่อไป นั่นคือหากให้ k เป็นจำนวนครั้งที่ทำจนสำเร็จ จะได้ว่า
ซึ่งดูจากสมการแล้วจะเข้าใจได้ไม่ยาก
ลองเขียนโปรแกรมแสดงการคำนวณตามสูตรตั้งแต่ k=1 ไปจนถึง k=10
p = 0.5
pk = []
for k in range(1,10+1):
pk += [p*(1-p)**(k-1)]
print(pk)ได้
[0.5, 0.25, 0.125, 0.0625, 0.03125, 0.015625, 0.0078125, 0.00390625, 0.001953125, 0.0009765625]วาดเป็นกราฟจะได้ว่า
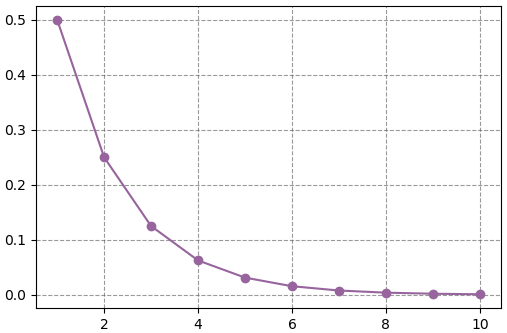
คราวนี้ลองเขียนโปรแกรมแสดงการทดลองจริงๆ โดยใช้ฟังก์ชัน Counter จากมอดูล collections เป็นตัวนับจำนวนผลที่ได้ (รายละเอียดวิธีใช้ https://phyblas.hinaboshi.com/20200413)
import random
from collections import Counter
pk = []
for i in range(1000):
k = 0
samret = 0
while(samret==0):
k += 1
if(random.randint(0,1)==1):
samret = 1
pk += [k]
print(Counter(pk))ได้
Counter({1: 504, 2: 254, 3: 120, 4: 60, 5: 29, 6: 17, 7: 6, 8: 6, 9: 1, 12: 1, 11: 1, 15: 1})หากวาดแผนภูมิแท่งแสดงการแจกแจงของผลที่ได้จะได้
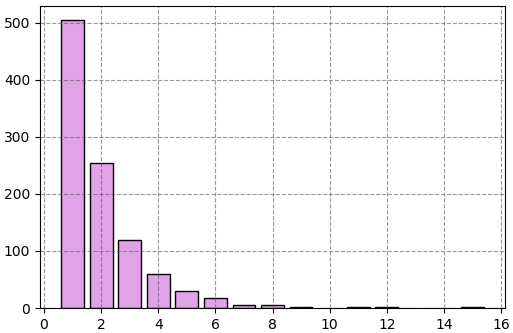
จะเห็นว่าการแจกแจงเป็นไปตามกราฟข้างต้น มีบางอันที่ฟลุกมากซึ่งกว่าจะสำเร็จก็ปาเข้าไปสิบกว่าครั้ง ซึ่งโอกาสเกิดมีน้อยกว่า 1 ใน 1000
จำนวนครั้งที่ทำกว่าจะสำเร็จสักครั้ง
ตัวอย่างที่ผ่านมาเป็นกรณีโยนเหรียญซึ่งมีความน่าจะเป็นเป็น 0.5 แต่หากมาลองคิดถึงกรณีทั่วไปที่ p เป็นค่าใดๆตั้งแต่ 0 ถึง 1 โอกาสที่จะสำเร็จในครั้งที่ k จะเป็น
นี่เป็นรูปแบบทั่วไปของการแจกแจงแบบเรขาคณิต
ซึ่งถ้าแทน p=0.5 ก็จะกลับไปสู่สมการกรณีโยนเหรียญ
ลองยกตัวอย่างเช่นว่ากำลังเล่นเกม RPG แล้วเราพยายามจะล่าไอเท็มจากมอนสเตอร์ตัวหนึ่ง โดยไอเท็มมีโอกาสดร็อปเป็น p แบบนี้จะต้องโค่นมอนสเตอร์ไปสักกี่ตัวจึงจะได้ไอเท็มที่ต้องการสักที?
ลองเขียนโปรแกรมให้แสดงการจากแจงเมื่อ p เป็นค่าต่างๆ
for i in range(1,100+1,5):
p = i*0.005
pk = []
for k in range(1,10+1):
pk += [p*(1-p)**(k-1)]
print(pk)หากวาดกราฟจะได้แบบนี้
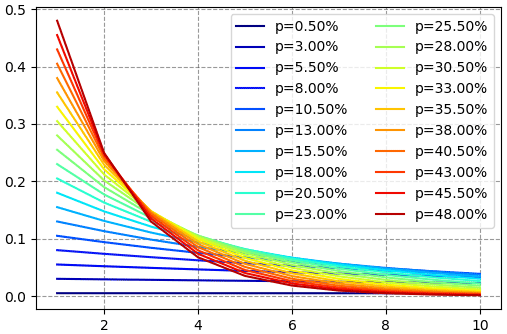
จะเห็นว่า k=1 คือได้ตั้งแต่ครั้งแรกเลยมีค่าสูงสุดเสมอ แต่ยิ่ง p น้อยโอกาสที่จะได้ตั้งแต่ครั้งแรกก็ยิ่งลดลง
ลองทดลองสุ่มดูจริงๆ ในกรณีที่ p=0.1
import random
from collections import Counter
p = 0.1
pk = []
for i in range(1000):
k = 0 # จำนวนครั้งที่ทำจนกว่าจะสำเร็จ
drop = 0 # 0 คือยังไม่สำเร็จ ถ้าสำเร็จแล้วจะเป็น 1
while(drop==0):
k += 1
# สุ่มเลข 1 ถึง 100 ถ้าได้ต่ำกว่า p คูณ 100 ก็ถือว่าสำเร็จ
if(random.randint(1,100)<=p*100):
drop = 1
pk += [k]
print(Counter(pk))ได้
Counter({1: 89, 2: 85, 4: 81, 3: 77, 5: 69, 6: 59, 7: 53, 8: 50, 9: 44, 10: 40, 13: 37, 15: 26, 12: 26, 14: 25, 16: 24, 11: 24, 20: 16, 17: 15, 18: 15, 26: 13, 23: 13, 19: 11, 21: 11, 28: 9, 25: 8, 29: 7, 27: 7, 33: 6, 32: 6, 34: 5, 22: 5, 36: 5, 30: 5, 43: 4, 24: 4, 35: 4, 39: 3, 45: 3, 31: 3, 38: 2, 49: 2, 42: 1, 50: 1, 46: 1, 48: 1, 40: 1, 37: 1, 63: 1, 41: 1, 44: 1})วาดแผนภูมิแท่งแสดงการแจกแจง
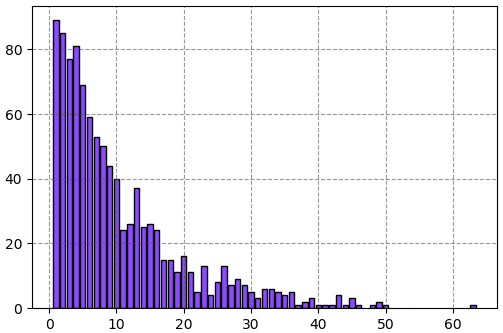
ค่าคาดหมายและความแปรปรวนของการแจกแจงแบบเรขาคณิต
ค่าคาดหมายของการแจกแจงแบบเรขาคณิตจะได้เป็น
ซึ่งก็สามารถเข้าใจที่มาได้ง่ายๆ ว่าเป็นเพราะหากเราทำการทดลองที่มีความน่าจะเป็นที่จะสำเร็จเป็น p ทำซ้ำๆหลายๆครั้งโดยเฉลี่ยแล้วก็ควรจะสำเร็จในครั้งที่ 1/p
ส่วนความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานจะได้เป็น
ตัวอย่างเช่นถ้าไปตีมอนสเตอร์ที่มีความน่าจะเป็นที่จะได้ไอเท็มที่ต้องการเป็น 1% จะคำนวณได้ว่า
ลองวาดภาพแสดงการแจกแจงพร้อมกับค่าคาดหมายและส่วนเบี่ยงเบนมาตรฐานจะได้แบบนี้
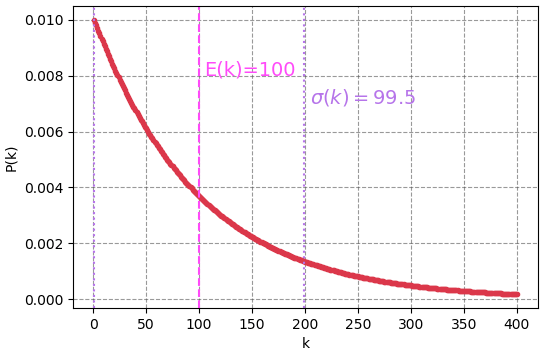
หมายความว่าน่าจะต้องตีประมาณ 100 ตัวจึงจะได้ อาจได้เร็วหรือช้ากว่านั้นแล้วแต่โชค ซึ่งความน่าจะเป็นว่าจะได้ในครั้งที่เท่าไหร่ก็แจกแจงตามนี้
การแจกแจงทวินามเชิงลบ
ที่จริงแล้วการแจกแจงแบบเรขาคณิตนั้นเป็นกรณีพิเศษของ การแจกแจงทวินามเชิงลบ (负二项分布, negative binomial distribution)
การแจกแจงทวินามเชิงลบเป็นการแจกแจงที่แสดงถึงความน่าจะเป็นที่จะสำเร็จ r ครั้งจากการทดลองทั้งหมด k ครั้ง
ซึ่งจะเห็นว่าลักษณะสมการออกมาคล้ายกับการแจกแจงทวินาม
และหากแทน r=1 ก็จะเป็นการแจกแจงแบบเรขาคณิต
กล่าวคือการแจกแจงแบบเรขาคณิตจะบอกว่าเมื่อไหร่จะสำเร็จครั้งแรก ส่วนการแจกแจงทวินามเชิงลบจะบอกว่าเมื่อไหร่จะสำเร็จครั้งที่ r
ค่าคาดหมายของการแจกแจงทวินามเชิงลบจะได้เป็น
ส่วนความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานจะได้เป็น
ยกตัวอย่างเช่นถ้าโค่นมังกรตัวหนึ่งได้จะมีโอกาสได้ลูกแก้มังกรอยู่ 2% เราต้องการลูกแก้วมังกรทั้งหมด r ลูก แบบนี้ควรจะต้องโค่นมังกรสักกี่ตัว?
ลองเขียนโปรแกรมคำนวณโดยให้ p=0.02 แล้วดูผลการแจกแจงที่ค่า r ต่างๆตั้งแต่ 1 ถึง 10
import math
p = 0.02
plt.figure(figsize=[6,4])
for r in range(1,10+1):
pk = []
for k in range(1,1000+1):
c = math.factorial(k+r-1)/(math.factorial(k)*math.factorial(r-1))
pk += [c*p**r*(1-p)**k]
print(pk) # แสดงค่าความน่าจะเป็นในกรณีของแต่ละค่า rวาดกราฟได้แบบนี้
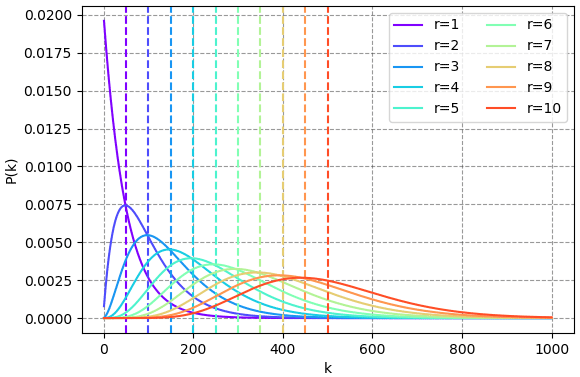
โดยในที่นี้เส้นประแนวตั้งแสดงถึงค่าคาดหมาย จะเห็นว่ามีค่ามากกว่าจุดสูงสุดเล็กน้อย โดยห่างออกไปไป 1/p ในที่นี้คือ 50
ต่อมาลองเขียนโค้ดเพื่อทำการสุ่มแล้วดูการแจกแจงที่ได้จริงๆ โดยลองดูกรณีที่ต้องการลูกแก้วมังกรทั้งหมด 7 ลูก
แต่ครั้งนี้ตัวเลขกระจายไปถึงค่าค่อนข้างสูง ดังนั้นจะขอแบ่งเป็นช่วงละ 20 แล้วนับรวมเป็นฮิสโทแกรมโดยใช้ฟังก์ชัน hist() ของ matplotlib วาด (รายละเอียดวิธีใช้เขียนไว้ใน numpy & matplotlib เบื้องต้น บทที่ ๑๓)
โค้ดเขียนได้ดังนี้
import random
import matplotlib.pyplot as plt
p = 0.02 # ความน่าจะเป็นที่จะดร็อปลูกแก้วมังกร
r = 7 # จำนวนลูกแก้วมังกรที่ต้องการ
pk = [] # ลิสต์เก็บจำนวนครั้งที่ทำจนกว่าจะได้
# ทำซ้ำหมื่นครั้ง
for i in range(10000):
k = 0 # จำนวนครั้งที่โค่นมังกร
n_drop = 0 # จำนวนครั้งที่ดร็อปลูกแก้วมังกร
# วนซ้ำจนกว่าจะได้ลูกแก้วมังกรครบ 7 ลูก
while(n_drop<r):
k += 1
# สุ่มค่าถึง 100 ถ้าได้ค่าไม่เกิน 100 คูณ p ก็ถือว่าดร็อปได้
if(random.randint(1,100)<=100*p):
n_drop += 1
pk += [k] # เก็บบันทึกเลขจำนวนครั้ง
plt.hist(pk,50) # วาดฮิสโทแกรม
plt.show()ได้ฮิสโทแกรมออกมาดังนี้ ซึ่งเป็นไปตามลักษณะกราฟแสดงการแจกแจงกรณีที่ r=7
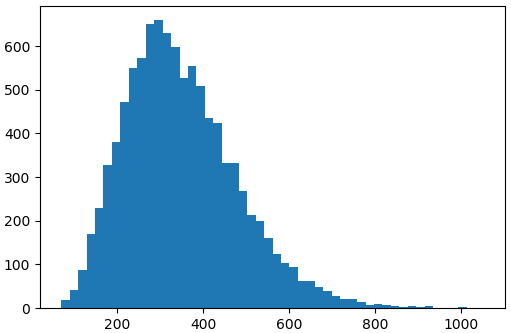
บทถัดไป >> บทที่ ๗