ต่อจาก บทที่ ๔

บทที่แล้วได้พูดถึงการแจกแจงความน่าจะเป็นของค่าแบบไม่ต่อเนื่องไปแล้ว สำหรับในบทนี้จะพูดถึงตัวอย่างการแจกแจงความน่าจะเป็นรูปแบบหนึ่งที่พบได้บ่อยและเข้าใจได้ไม่ยาก นั่นคือการแจกแจงทวินาม (二项分布, binomial distribution)




การแจกแจงผลการโยนเหรียญ

ก่อนจะพูดถึงว่าการแจกแจงทวินามคืออะไร ขอเริ่มจากยกตัวอย่างการแจกแจงผลการโยนเหรียญ ซึ่งเป็นตัวอย่างการแจกแจงทวินามในรูปแบบที่ง่ายที่สุด

สมมุติว่ามีเหรียญ n เหรียญซึ่งมีโอกาสโยนแล้วได้หัวหรือก้อยเป็น 1/2 เท่ากัน ผลรวมจำนวนครั้งที่จะโยนได้หัวควรจะเป็นเท่าใด

กรณีนี้จำนวนครั้งที่โยนได้หัวคือตัวแปรสุ่ม เพราะขึ้นอยู่กับว่าโยนเหรียญ n ครั้งออกอะไรบ้าง แต่ละค่าก็มีความน่าจะเป็นต่างกันไป

สมมุติว่า ◎ แทนหัส ◯ แทนก้อย โยนเหรียญ 1 ครั้งมีโอกาสจะได้ 2 กรณีคือเหรียญนั้นเป็น ◎ กับ ◯

ให้ P(k) เป็นความน่าจะเป็นที่จะโยนเหรียญได้หัว k ครั้ง กรณีโยนเหรียญครั้งเดียวจะได้ว่า


ถ้าโยน 2​ ครั้งก็จะแบ่งเป็น 4 กรณี คือ ◎◎, ◎◯, ◯◎, ◯◯ ดังนั้นความน่าจะเป็นจะกลายเป็น


ถ้าโยน 3 ครั้งก็จะมี 8 กรณีคือ ◎◎◎, ◎◎◯, ◎◯◎, ◎◯◯, ◯◎◎, ◯◎◯, ◯◯◎, ◯◯◯ ดังนั้นความน่าจะเป็นจะกลายเป็น


ถ้าโยน 4 ครั้งก็จะมี 16 กรณีคือ
◎◎◎◎, ◎◎◎◯, ◎◎◯◎, ◎◎◯◯,
◎◯◎◎, ◎◯◎◯, ◎◯◯◎, ◎◯◯◯,
◯◎◎◎, ◯◎◎◯, ◯◎◯◎, ◯◎◯◯,
◯◯◎◎, ◯◯◎◯, ◯◯◯◎, ◯◯◯◯

ดังนั้นความน่าจะเป็นจะกลายเป็น


ไล่มาถึงตรงนี้ก็จะพอนึกภาพได้ออกว่าการแจกแจงแนวโน้มจะเป็นอย่างไรเมื่อเพิ่มจำนวนเหรียญขึ้นไป

หากโยนเหรียญ n ครั้งความน่าจะเป็นที่จะได้หัว k ครั้งเป็น


โดย C(n,k) คือจำนวนวิธีการในการจัดหมู่ (combination) ซึ่งคำนวณได้โดย


โดยเครื่องหมายตกใจในที่นี้หมายถึงแฟกทอเรียล

ในไพธอนมีฟังก์ชัน factorial() ในมอดูล math เอาไว้คำนวณค่าแฟทอเรียลได้ ลองเอามาใช้เขียนโปรแกรมเพื่อแสดงการแจกแจงตั้งแต่ n=1 ไปจนถึง n=9 ดูได้ดังนี้

import math
# n คือจำนวนเหรียญทั้งหมด
for n in range(1,9+1):
    n_hua = [] # ลิสต์เก็บความถี่ในแต่ละกรณีจำนวนที่ได้หัว k ตัว
    # k คือจำนวนเหรียญที่จะได้หัว
    for k in range(0,n+1):
        c = math.factorial(n)/(math.factorial(k)*math.factorial(n-k))
        n_hua += [c/2**n]
    print('n =',n,':',n_hua) # แสดงผล

ได้

n = 1 : [0.5, 0.5]
n = 2 : [0.25, 0.5, 0.25]
n = 3 : [0.125, 0.375, 0.375, 0.125]
n = 4 : [0.0625, 0.25, 0.375, 0.25, 0.0625]
n = 5 : [0.03125, 0.15625, 0.3125, 0.3125, 0.15625, 0.03125]
n = 6 : [0.015625, 0.09375, 0.234375, 0.3125, 0.234375, 0.09375, 0.015625]
n = 7 : [0.0078125, 0.0546875, 0.1640625, 0.2734375, 0.2734375, 0.1640625, 0.0546875, 0.0078125]
n = 8 : [0.00390625, 0.03125, 0.109375, 0.21875, 0.2734375, 0.21875, 0.109375, 0.03125, 0.00390625]
n = 9 : [0.001953125, 0.017578125, 0.0703125, 0.1640625, 0.24609375, 0.24609375, 0.1640625, 0.0703125, 0.017578125, 0.001953125]

ลักษณะเหมือนเป็นพีรามิดซ้อนกันไปเรื่อยๆ

หากเอาค่าที่ได้นี้มาวาดกราฟแสดงการแจกแจงจะได้เป็นแบบนี้



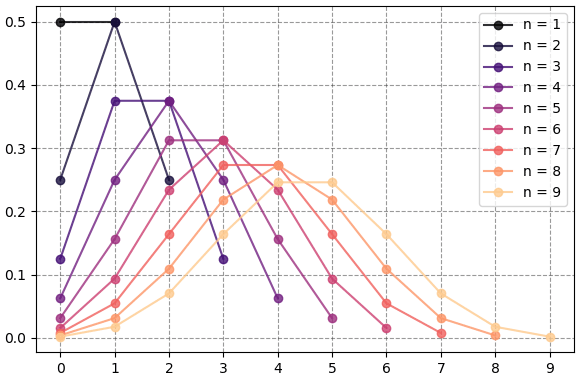
กราฟที่ได้จะมีลักษณะสมมาตรซ้ายขวา โดยค่าสูงสุดของกราฟจะอยู่ตรงกลาง กรณีแบบนี้ค่าคาดหมายก็จะอยู่ตรงกลางซึ่งเป็นจุดสูงสุดด้วย ซึ่งจะเห็นได้ว่าจุดสูงสุดอยู่ที่ n/2

ลองมาทดลองสุ่มจริงๆโดยใช้ randint ดู

import random
n = 9 # จำนวนเหรียญ
p = [0]*(n+1) # ลิสต์เก็บค่าความถี่ของจำนวนที่ออกหัวที่ได้ตั้งแต่ 0 ถึง n
# ทำซ้ำ 10000 ครั้ง
for i in range(10000):
    n_hua = 0 # จำนวนครั้งที่ออกหัว
    # ทำซ้ำ n ครั้ง
    for j in range(n):
        # สุ่ม 0 (ก้อย) หรือ 1 (หัว) ถ้าได้หัวก็บวกเพิ่ม
        n_hua += random.randint(0,1)
    # วนครบ n ครั้ง ได้จำนวนครั้งที่ออกหัว n_hua
    p[n_hua] += 1 # เพิ่มความถี่สำหรับจำนวนหัว n_hua ที่ได้นั้น
print(p) # แสดงผลความถี่สุดท้ายของแต่ละค่าที่ได้ออกมา

ได้

13, 177, 691, 1690, 2441, 2447, 1652, 703, 158, 28]

ถ้าวาดเป็นแผนภูมิแท่งแสดงก็จะได้แบบนี้



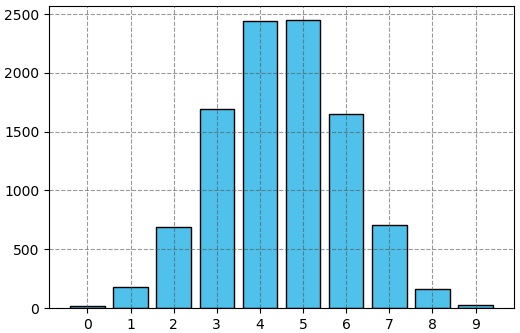
จะเห็นว่าการแจกแจงเป็นไปตามความน่าจะเป็นกรณี n=9 ซึ่งได้คำนวณไว้ข้างต้น

ลองปรับค่าจำนวนเหรียญ n ก็จะได้การแจกแจงที่ต่างกันออกไปตามที่ควรจะเป็น




การแจกแจงผลการโยนลูกเต๋า

ต่อไปจะพูดถึงที่มาของการแจกแจงแบบนี้ และขยายความไปสู่กรณีทั่วไปมากขึ้น

ที่จริงแล้วผลที่ได้นี้เป็นไปตามทฤษฎีบททวินาม (binomial theorem) ซึ่งว่าด้วยการแจกแจงของ (x+y)ⁿ


ซึ่งจะได้ว่า


ในที่นี้ x แสดงถึงเหรียญที่ออกหัว y แสดงถึงเหรียญที่ออกก้อย โดยเลขชี้กำลังของ x แสดงถึงจำนวนเหรียญที่ออกหัว ดังนั้นสัมประสิทธิ์ของแต่ละพจน์จะแสดงความถี่ของการออกเป็นจำนวนครั้งเท่านั้น

ซึ่งสัมประสิทธิ์นี้ก็คือ C(n,k) ดังนั้นเมื่อหารด้วยจำนวนเหตุการณ์ทั้งหมด ซึ่งก็คือ 2ⁿ ก็จะเป็นความน่าจะเป็นที่จะออกหัวเป็นจำนวนครั้งเท่านั้น


การโยนเหรียญหัวก้อยนั้นเป็นตัวอย่างกรณี ๒ ทางเลือกที่มีโอกาสเท่าๆกันคือ 1/2 แต่เหตุการณ์โดยทั่วไปอาจมีความน่าจะเป็นในการเกิดขึ้นเป็นเท่าไหร่ก็ได้ตั้งแต่ 0 ถึง 1

ยกตัวอย่างเช่นทอยลูกเต๋าแล้วพิจารณาเหตุการณ์ที่จะได้ 1 กับเหตการณ์ที่จะได้แต้มอื่น แบบนี้ความน่าจะเป็นที่จะทอยได้ 1 คือ


กรณีนี้จะต่างจากกรณีโยนเหรียญตรงที่โอกาสมีแค่ 1/6 ไม่ใช่ 1/2 โอกาสไม่ได้เท่ากัน ดังนั้นจะแจกแจงแบบกรณีโยนเหรียญไม่ได้

การโยนเหรียญนั้นเทียบได้กับ ((x+y)/2)ⁿ แต่ถ้าโอกาสไม่เท่ากันก็จะเปลี่ยนเป็นตามสัดส่วนนั้น เช่นกรณีลูกเต๋าก็จะเป็น


ลองเขียนโปรแกรมแสดงการแจกแจงเช่นเดียวกับกรณีโยนเหรียญ

import math
for n in range(1,24+1):
    n_dai1 = [] # ลิสต์เก็บความถี่
    # k คือจำนวนหน้าลูกเต๋าที่ออกแต้ม 1
    for k in range(0,n+1):
        c = math.factorial(n)/(math.factorial(k)*math.factorial(n-k))
        n_dai1 +=[c*((1/6)**k)*((5/6)**(n-k))]
    print('n = %d:\n'%n, n_dai1)

ค่าที่แสดงออกมาจะมีเยอะมาก ในที่นี้ของไม่นำมาแสดงตรงนี้ แต่หากวาดกราฟก็จะได้เช่นนี้



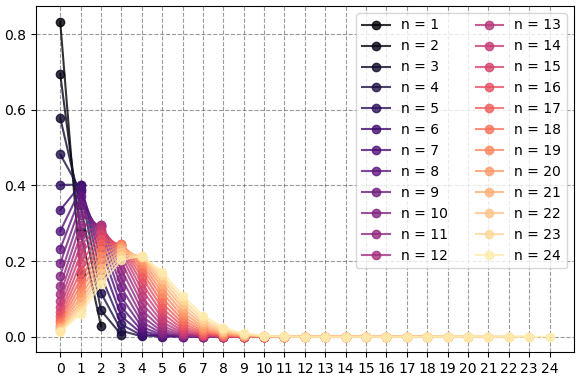
การแจกแจงส่วนใหญ่จะอยู่ในส่วนของจำนวนน้อยๆ โดยจุดสูงสุดในกรณีที่ลูกเต๋าเป็น 6,12,18,24 คือ 1,2,3,4 ตามลำดับ ซึ่งก็เป็นไปตามสามัญสำนึกที่ว่าถ้าโอกาส 1/6 โยน 6 ครั้งก็ควรจะได้ครั้งหนึ่ง

คราวนี้จำลองการโยนลูกเต๋าดู

import random
n = 24 # จำนวนเหรียญ
p = [0]*(n+1) # ลิสต์เก็บค่าความถี่ของจำนวนที่หน้าเต๋าได้แต้ม 1 ได้ตั้งแต่ 0 ถึง n
# ทำซ้ำ 10000 ครั้ง
for i in range(10000):
    n_dai1 = 0 # บวกสะสมจำนวนครั้งที่ได้แต้ม 1
    for j in range(n):
        # สุ่มเลข 1-6 ถ้าได้ 1 ก็บวกเพิ่ม
        if(random.randint(1,6)==1):
            n_dai1 += 1
    p[n_dai1] += 1
print(p) # แสดงผลความถี่สุดท้ายของแต่ละค่าที่ได้ออกมา

ได้

[116, 626, 1372, 2075, 2153, 1706, 1076, 539, 208, 88, 31, 8, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

ซึ่งก็สอดคล้องกับการกระจายความน่าจะเป็นที่คำนวณได้ และจะเห็นว่าตัวหลังๆเป็น 0 หมดเพราะความเป็นไปได้ต่ำมาก

นำมาวาดแผนภูมิแท่งแสดงความถี่ก็จะได้แบบนี้






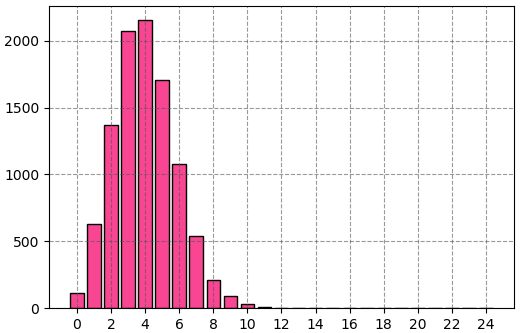
รูปทั่วไปของการแจกแจงทวินาม

จากตัวอย่างกรณีโยนเหรียญและทอยลูกเต๋า สามารถนำไปสู่กรณีที่ทั่วไปกว่านั้น คือหากแบ่งเป็นเกิดกับไม่เกิดเหตุการณ์ที่พิจารณา โดยมีค่าความน่าจะเป็นที่จะเกิดเหตุการณ์เป็น p การแจกแจงจะได้เป็น


นำมาลองแจกแจงจนถึง 5 จะได้เป็นลักษณะแบบนี้


ดังนั้นความน่าจะเป็นที่จะได้ผลที่ต้องการ k ครั้งก็จะเป็นไปตามสัมประสิทธิ์ที่นำหน้า นั่นคือ


นี่ก็คือรูปทั่วไปของการแจกแจงความน่าจะเป็นแบบทวินาม

ตรงนี้ถ้า p=1/2 ก็จะกลับไปสู่สมการของกรณีการโยนเหรียญหัวก้อย

ถ้า n=1 จะเป็นกรณีเฉพาะที่เรียกว่าเป็นการแจกแจงแบร์นุลลี (伯努利分布, Bernoulli distribution)





การแจกแจงเหตุการณ์ที่มีโอกาสเกิดขึ้นเป็น p

ยกตัวอย่างสถานการณ์เช่นเวลาที่เล่นเกมที่มีการตีมอนสเตอร์ เมื่อชนะเสร็จก็จะมีโอกาสดร็อปไปเท็ม สมมุติว่าเมื่อฆ่ามังกรได้มีโอกาสได้เขียวมังกรอยู่ 5% (หรือ 1/20) ถ้าฆ่ามังกรไป n ตัวจะได้เขี้ยวมังกรสักกี่อัน

ใช้สูตรแจกแจงทวินามมาคำนวณอีกเช่นเคย คราวนี้ p=1/20 ลองดูกรณีที่ n เป็น 10,20,...,200

import math
p = 1/20
for n in range(10,200+1,10):
    n_drop = []
    for k in range(0,n+1): # k คือจำนวนไอเท็มที่ดร็อปได้
        c = math.factorial(n)/(math.factorial(k)*math.factorial(n-k))
        n_drop +=[c*(p**k)*((1-p)**(n-k))]    
    print('n = %d:\n'%n, n_drop)

ผลที่ได้ถ้านำมาวาดกราฟก็จะได้แบบนี้ ในที่นี้ขอแสดงแค่ช่วงจนถึง k=20 แม้ว่าค่าจริงๆจะมีถึง 200 เพราะถัดจากตรงนี้ไปก็แทบเป็น 0 หมดแล้ว



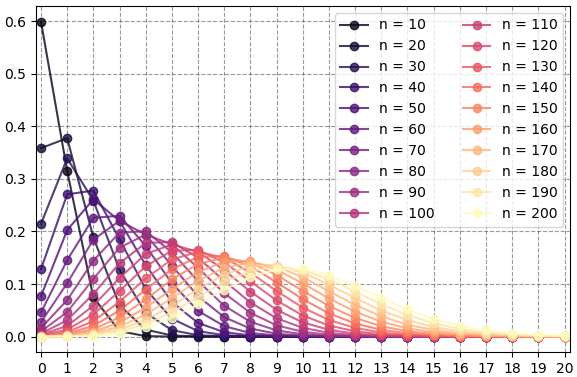
คราวนี้ก็ทดลองเขียนโปรแกรมสุ่มดูจริงๆอีก

import random
n = 200 # จำนวนมอนสเตอร์ที่จัดการไป
p = [0]*(30+1) # ลิสต์เก็บจำนวนที่ดร็อปได้ เอาถึงแค่ 30 ก็พอ
# ทำซ้ำ 10000 ครั้ง
for i in range(10000):
    n_drop = 0 # บวกสะสมจำนวนครั้งที่ดร็อปได้
    for j in range(n):
        # สุ่มเลข 1-100 ถ้าได้ไม่เกิน 5 ถือว่าได้
        if(random.randint(1,100)<=5):
            n_drop += 1
    if(n_drop<=30): # บันทึกเฉพาะที่ไม่เกิน 30
        p[n_drop] += 1
print(p) # แสดงผลความถี่สุดท้ายของแต่ละค่าที่ได้ออกมา

ได้

[0, 5, 21, 63, 171, 382, 639, 956, 1090, 1242, 1259, 1197, 959, 708, 541, 339, 185, 133, 60, 22, 19, 4, 3, 1, 1, 0, 0, 0, 0, 0, 0]

ถ้านำมาวาดแผนภูมิแท่งดูการแจกแจงก็จะได้



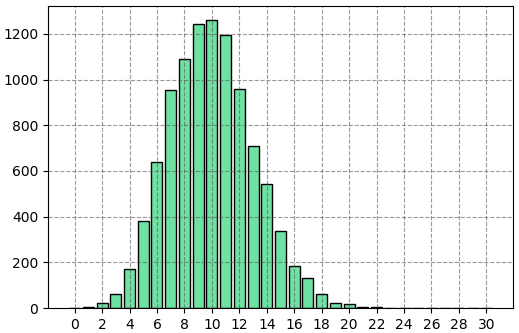
ค่าสูงสุดอยู่ที่ 10 สอดคล้องกับที่ควรจะเป็นว่าถ้าโอกาสดร็อป 1/20 จัดการไป 200 ก็จะได้มา 200/20=10




ค่าคาดหมายของการแจกแจงทวินาม

ถ้านำการแจกแจงทวินาม n ครั้งที่ความน่าจะเป็น p มาหาค่าคาดหมายจะได้


ถ้า np เป็นจำนวนเต็ม ตรงนั้นก็จะเป็นจุดยอดสูงสุดด้วย

ซึ่งตรงนี้แสดงให้เห็นว่า หากทำอะไรที่มีโอกาสทำสำเร็จได้ 1 ใน n พอทำไป n ครั้งก็ควรจะต้องทำสำเร็จ 1 ครั้ง ถ้าทำ 2n ครั้งก็จะสำเร็จ 2 ครั้ง ซึ่งก็ตรงกับสามัญสำนึก ส่วนโอกาสที่จะได้เป็นจำนวนอื่นก็ลดหลั่นลงไปจากนี้ จะเป็นเท่าใดก็ดูได้จากการแจกแจง

วิธีพิสูจน์






ค่าความแปรปรวนของการแจกแจงทวินาม

ค่าความแปรปรวนของการแจกแจงทวินามคือ


พิสูจน์ได้ดังนี้


โดยค่าคาดหวัง E(k)=np




บทถัดไป >> บทที่ ๖

~ เกี่ยวกับเรา ~

สารบัญ

รวมคำแปลวลีเด็ดจากญี่ปุ่น

ภาษา python มอดูลต่างๆ -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch การเรียนรู้ของเครื่อง -- โครงข่าย      ประสาทเทียม

ภาษา javascript

ภาษา mongol

ภาษาศาสตร์

maya

ความน่าจะเป็น

บันทึกในญี่ปุ่น

บันทึกในจีน -- บันทึกในปักกิ่ง -- บันทึกในฮ่องกง -- บันทึกในมาเก๊า

บันทึกในไต้หวัน

บันทึกในยุโรปเหนือ

บันทึกในประเทศอื่นๆ

qiita

บทความอื่นๆ

บทความแบ่งตามหมวด

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --sql --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา บันทึก เรื่องแต่ง ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม

　 ค้นหาบทความ

　 บทความล่าสุด

　 บทความแนะนำ

บทความแต่ละเดือน

ค้นบทความเก่ากว่านั้น

ไทย

日本語

中文