ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๙: การแจกแจงความน่าจะเป็นที่ขึ้นกับตัวแปรสองตัวขึ้นไป
เขียนเมื่อ 2020/07/27 07:07
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๘
ในบทนี้ยังอยู่ที่เรื่องของการแจกแจงความน่าจะเป็นของค่าแบบต่อเนื่องต่อจากบทที่แล้ว คราวนี้จะว่าด้วยการแจกแจงที่ขึ้นอยู่กับตัวแปร 2 ตัวขึ้นไป
ในที่นี้จะยกตัวอย่างกรณีที่มีตัวแปร 2 ตัว ซึ่งสามารถวาดให้มองเห็นภาพได้ ส่วนกรณีที่มีตัวแปรมากกว่า 2 ตัวอาจจินตนาการภาพได้ยาก แต่ก็สามารถต่อยอดไปได้
การแจกแจงความน่าจะเป็นร่วม
ในบทแล้วได้พิจารณาการแจกแจงที่ขึ้นอยู่กับตัวแปรตัวเดียว ซึ่งสามารถนึกภาพง่ายๆได้ว่ามีฟังก์ชันแจกแจงเป็นกราฟ แล้วพื้นที่ใต้กราฟก็จะเป็นความน่าจะเป็นของช่วงนั้น ซึ่งก็หาได้จากปริพันธ์
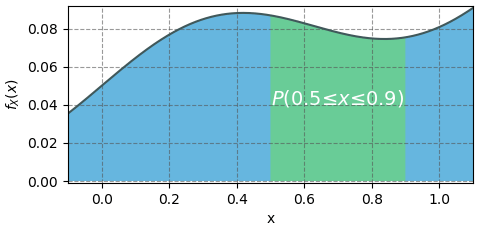(ภาพ 9.1)
(สมการ 9.1)
คราวนี้ลองจินตนาการถึงกรณีที่ขึ้นกับตัวแปร 2 ตัว
เมื่อมี 2 ตัวแปร เวลาจะวาดกราฟจึงเป็นสองมิติ แต่พอจะวาดค่าของฟังก์ชันแจกแจงความหนาแน่นด้วยจึงอยู่ในรูปของสามมิติแบบนี้
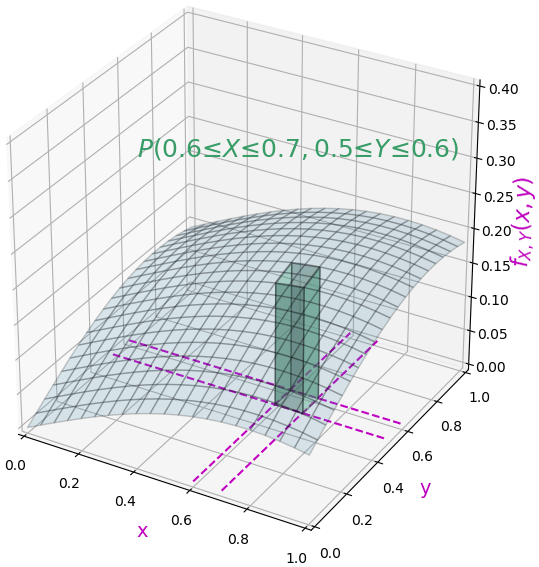
แบบนี้ค่าความน่าจะเป็นของค่าในช่วง x และ y ที่กำหนดก็คือปริมาตรใต้กราฟ ซึ่งคำนวณได้โดยการหาปริพันธ์ในช่วงโดยคิดทั้ง x และ y
ขอบเขตในที่นี้กำหนดทั้งใน x และ y พร้อมกัน จึงหมายความว่าเป็นความน่าจะเป็นร่วม เวลาเขียนจะใช้จุลภาค (,) คั่นเพื่อแสดงให้เห็นว่าดูขอบเขตของทั้ง x และ y
ความน่าจะเป็นรวมทั้งหมดต้องเป็น 1 ดังนั้นพื้นที่ใต้กราฟรวมก็เป็น 1 ปริพันธ์ตั้งลบอนันต์ถึงอนันต์ก็ต้องได้ 1
หากต้องการหาความน่าจะเป็นโดยดูแค่ค่า x อย่างเดียวในขณะที่ y จะเป็นค่าใดๆนั้นก็ทำได้โดยหาปริพันธ์ของ y ตลอดช่วง
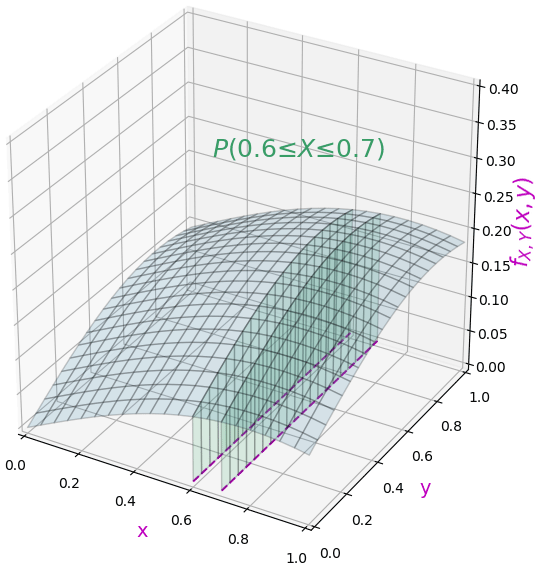
ซึ่งพอไม่สนการแจกแจงในแกน y แบบนี้อาจมองว่า f กลายเป็นแค่ฟังก์ชันของ x เท่านั้น แล้วจะเขียนได้ว่า
แล้วก็จะได้ว่า
ซึ่งก็จะกลับไปสู่สมการ 9.1 แล้วก็จะกลับไปเขียนเป็นสองมิติอย่างในภาพ 9.1 ได้
ในทางกลับกันถ้าจะมองแค่การแจกแจงในแกน y โดยไม่สนใจแกน x ก็จะกลายเป็นแบบนี้
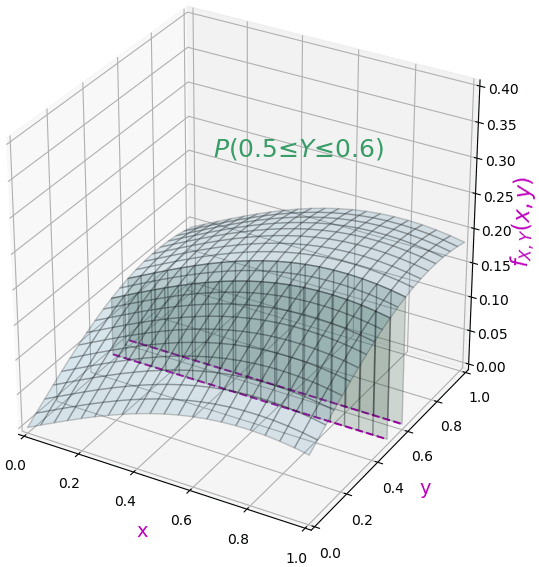
การแจกแจงความน่าจะเป็นแบบมีเงื่อนไข
จากตัวอย่างที่ผ่านมาเราได้พิจารณาฟังก์ชันแจกแจงที่ขึ้นอยู่กับ 2 ตัวแปรไปในขณะเดียวกันคือ x และ y และเมื่อต้องการพิจารณาแค่ตัวแปรใดตัวหนึ่งก็ให้ทำการหาปริพันธ์ของอีกตัวแปรหนึ่งตลอดตั้งแต่ลบอนันต์ถึงอนันต์
แต่นอกจากนี้แล้ว ยังสามารถสร้างฟังก์ชันแจกแจงความน่าจะเป็นของตัวแปรตัวเดียวโดยที่พิจารณาให้อีกตัวแปรอยู่แค่ในช่วงที่กำหนดได้
หากต้องการหาความน่าจะเป็นตาม x โดยที่พิจารณา y แค่ช่วงใดช่วงหนึ่ง อาจเขียนภาพได้ในลักษณะนี้
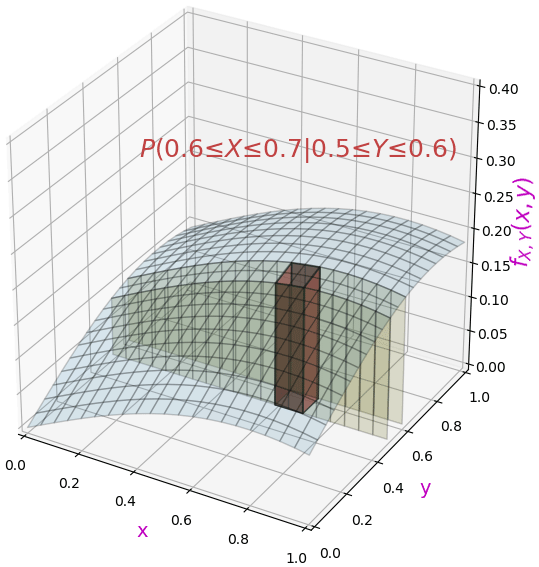
แบบนี้เป็นความน่าจะเป็นแบบมีเงื่อนไข ที่ X อยู่ในช่วง x1 ถึง x2 โดยมีเงื่อนไขคือค่า Y อยู่ระหว่าง y1 ถึง y2 ซึ่งก็คือความน่าจะเป็นร่วมของทั้ง X และ Y หารด้วยความน่าจะเป็นเฉพาะ Y ก็จะคิดได้ว่าเป็นปริมาตรส่วนสีแดงหารด้วยส่วนสีเหลือง
ซึ่งสามารถทำเป็นฟังก์ชันแจกแจงของ X เฉพาะในช่วง y1 ถึง y2 ได้
แล้วความน่าจะเป็นที่ X จะอยู่ในช่วง x1 ถึง x2 เมื่อ Y อยู่ระหว่าง y1 ถึง y2 ก็จะคำนวณได้ด้วยฟังก์ชันแจกแจงความน่าจะเป็นอันนี้
นอกจากนี้ ที่จริงค่าของตัวแปรอีกตัวอาจไม่จำเป็นต้องเป็นขอบเขตก็ได้ แต่เป็นค่าค่าหนึ่ง
เช่นถ้าพิจารณาความน่าจะเป็นแค่ที่ Y=y1 อาจได้ว่า
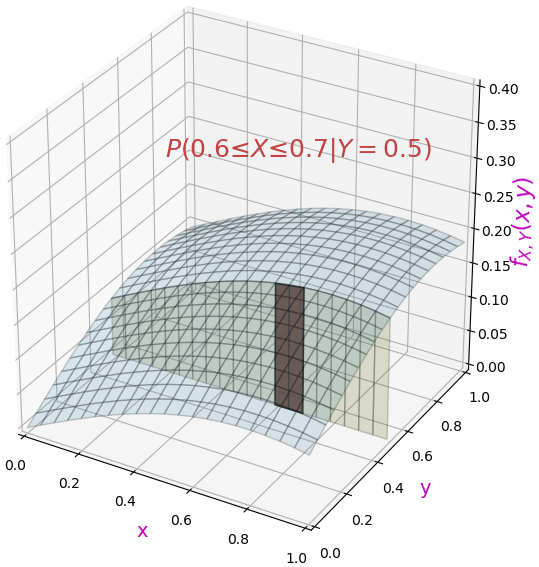
ซึ่งที่จริงแล้วในกรณีฟังก์ชันต่อเนื่องแบบนี้การจะมาคิดความน่าจะเป็นที่ค่าค่าหนึ่งนั้นจะต้องได้ 0 เสมอ เพราะจากภาพถ้าดูเป็นปริมาตร ไม่ว่าจะส่วนสีแดงหรือสีเหลืองก็แบนเป็นแผ่น จึงเข้าใกล้ 0 ทั้งนั้น
แต่เพราะเข้าใกล้ 0 เช่นกัน ผลหารระหว่างส่วนสีแดงกับสีเหลืองก็มีค่าได้ ซึ่งก็คือดูจากพื้นที่ของหน้าตัดตรงนั้นนั่นเอง
ดังนั้นความว่าจะเป็นเมื่อ Y=y1 หาได้ว่า
โดย
และในทำนองเดียวกัน ถ้าพิจารณาการแจกแจงความน่าจะเป็นตาม Y โดยที่ X เท่ากับค่าหนึ่ง ก็จะเป็น
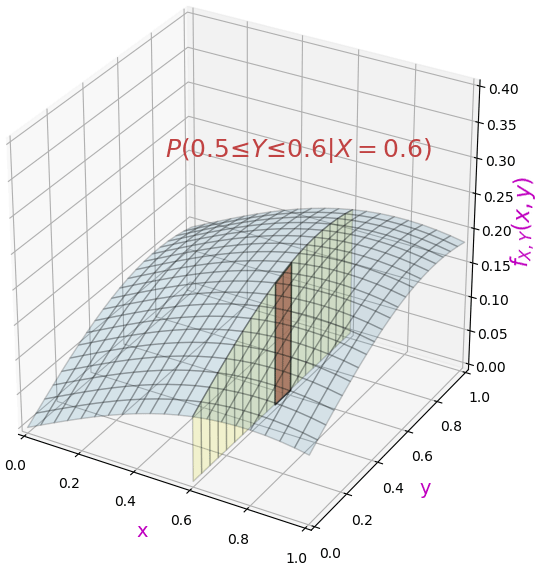
ความเป็นอิสระจากกัน
ถ้าการแจกแจงตามตัวแปรหนึ่งไม่ได้มีผลต่อการแจกแจงตามในอีกตัวแปร นั่นคือเป็นอิสระต่อกัน สามารถแยกส่วนของฟังก์ชันการแจกแจงของทั้ง 2 ตัวแปรออกจากกันได้
ตัวอย่างเช่น
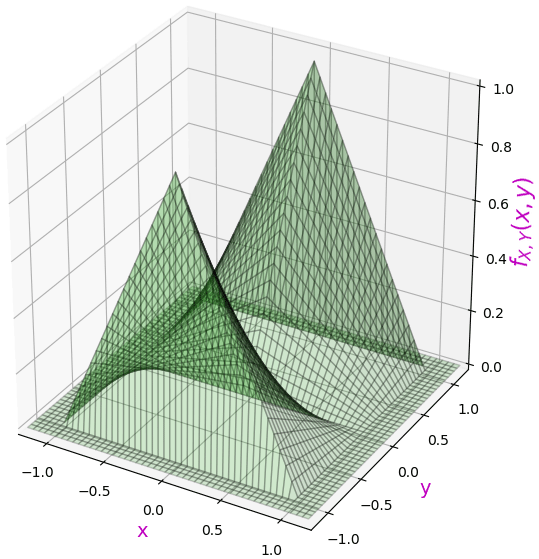
ถ้าลองดูการแจกแจงตาม x ที่ค่า y ค่าต่างๆ ก็จะเห็นว่ามีความแตกต่างเป็นจำนวนเท่าแน่นอน เหมือนคูณด้วยค่าคงที่บางอย่างเท่านั้น
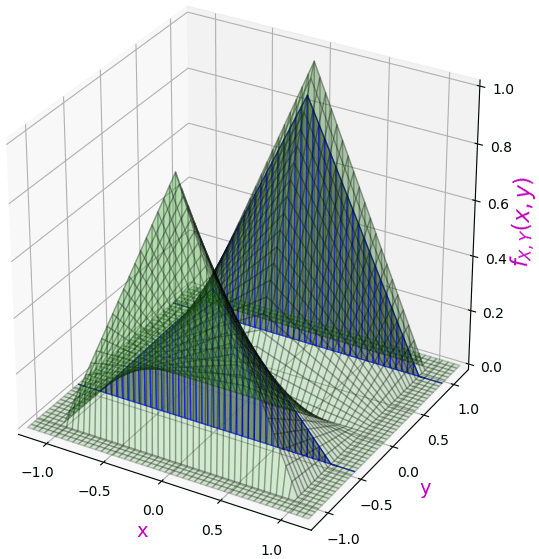
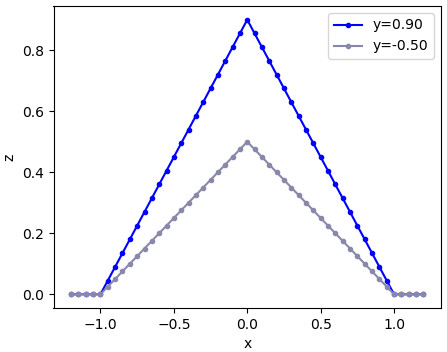
เมื่อลองดูการแจกแจงตาม y ที่ค่า x ค่าต่างๆก็เช่นกัน
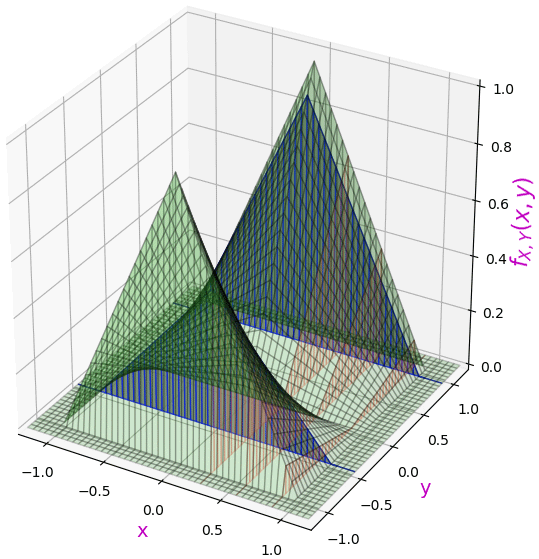
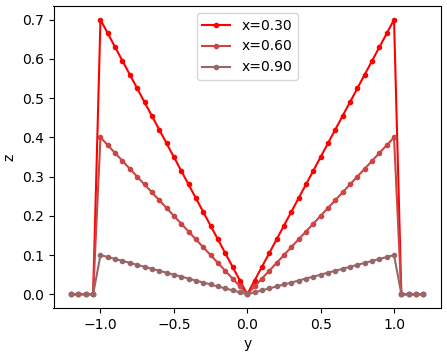
ดังนั้นกรณีแบบนี้สามารถแยกฟังก์ชันแจกแจงตาม x และตาม y ออกจากกันได้
ค่าคาดหมาย
ฟังก์ชันแจกแจงของ 2 ตัวแปรก็สามารถคำนวณค่าคาดหมายได้ในทำนองเดียวกันกับกรณีตัวแปรเดียว
g(X,Y) เป็นฟังก์ชันใดๆของ X และ Y ค่าคาดหมายของ g(X,Y) คำนวณได้โดย
เช่น ค่าคาดหมายของ X และ Y เป็น
ตัวอย่างเช่น ถ้าฟังก์ชันแจกแจงความน่าจะเป็นเป็นดังนี้
ถ้าหาค่าคาดหมายของ XY จะได้
บทถัดไป >> บทที่ ๑๐