ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๐: การแจกแจงแบบเลขชี้กำลัง
เขียนเมื่อ 2020/07/27 14:41
แก้ไขล่าสุด 2023/08/26 13:22
ต่อจาก บทที่ ๙
ตั้งแต่บทที่ ๘ ได้เริ่มทำความเข้าใจเกี่ยวกับการการแจกแจงความหนาแน่นของความน่าจะเป็นของค่าแบบต่อเนื่องไปแล้ว
บทนี้จะเป็นเรื่องของการแจกแจงของค่าต่อเนื่องรูปแบบหนึ่งที่พบได้บ่อย นั่นคือการแจกแจงแบบเลขชี้กำลัง (指数分布, exponential distribution)
ระยะห่างของการเกิดเหตุการณ์แบบสุ่ม
สมมุติว่ามีเหตุการณ์บางอย่างที่เกิดขึ้นในช่วงเวลาหนึ่งในแบบสุ่ม โดยความน่าจะเป็นที่จะเกิดเหตุการณ์ในแต่ละช่วงจะมีพอๆกันหมดภายในช่วง หรือก็คือเป็นการแจกแจงแบบเอกรูป
หากคิดง่ายๆแล้วโดยทั่วไประยะห่างระหว่างเหตุการณ์โดยเฉลี่ยควรจะเป็นระยะเวลาหารด้วยจำนวนเหตุการณ์ แต่ในการสุ่มขึ้นมาจริงๆจะพบว่ามีบางช่วงห่างกันมากหรือน้อยกว่าค่าเฉลี่ย
การแจกแจงค่าระยะห่างของเหตุการณ์นั้นจะเป็นการแจกแจงแบบเลขชี้กำลัง
ยกตัวอย่างเช่น ฝูงนกอพยพ 3600 ตัวบินผ่านเข้าชายแดนประเทศมา มีคนจับเวลาไว้ว่าตั้งแต่นกตัวแรกเริ่มผ่านมาจนตัวสุดท้ายผ่านไปใช้เวลาทั้งหมด 10 ชั่วโมง ถามว่าระยะเวลาที่แต่ละตัวผ่านนั้นจะเว้นช่วงห่างกันแค่ไหน
10 ชั่วโมงก็คือ 36000 มีนก 3600 ตัว ดังนั้นโดยเฉลี่ยแล้วแต่ละตัวควรจะเว้นช่วงกันประมาณ 36000/3600 = 10 วินาที
ลองทดลองสุ่มแล้ววาดฮิสโทแกรมแจกแจง
import random
wela = [] # เก็บเวลาที่แต่ละตัวผ่าน
n = 3600 # สุ่ม 3600 ครั้ง
t = 36000 # ในระยะเวลา 36000 วินาที
for i in range(n):
# ค่าเวลาอยู่ในช่วงตั้งแต่ 0 ถึง 36000
wela += [random.uniform(0,t)]
# จัดเรียงลำดับใหม่ตามค่าเวลา
wela = sorted(wela)
wenwang = [] # ดูระยะห่างทีละคู่
for i in range(1,n):
# เวลาลำดับที่ i ลบด้วยเวลาลำดับที่ i-1
wenwang += [wela[i]-wela[i-1]]
print('ระยะห่างเฉลี่ย = %.2f'%(sum(wenwang)/(n-1))) # ได้ 10.00
plt.xlabel('ระยะห่างเวลา',family='Tahoma')
plt.ylabel('จำนวน',family='Tahoma')
# วาดฮิสโทแกรม
plt.hist(wenwang,100,ec='#000000')
plt.show()ผลที่ได้จะเห็นการแจกแจงที่มีลักษณะลดหลั่นลงไปเรื่อยๆแบบเลขชี้กำลัง
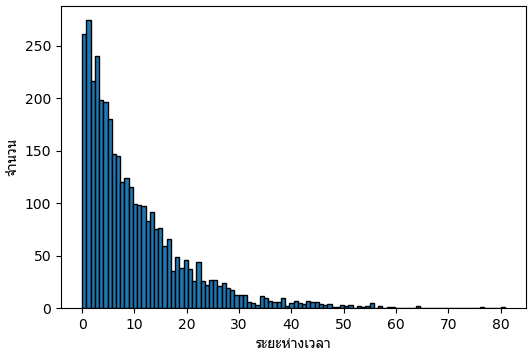
ฟังก์ชันความหนาแน่นของความน่าจะเป็นและฟังก์ชันแจกแจงความหนาแน่นสะสม
เมื่อได้เห็นการแจกแจงจากการทดลองสุ่มจริงไปแล้ว คราวนี้ลองมาดูสมการที่จะมาอธิบายผลลัพธ์ที่ได้นั้น ซึ่งก็คือการแจกแจงแบบเลขชี้กำลัง
หากเหตุการณ์เกิดโดยเฉลี่ย λ ครั้งเมื่อเวลาผ่านไป 1 วินาที (หรือหน่วยเวลาใดๆก็ได้) แล้ว
ฟังก์ชันความหนาแน่นของความน่าจะเป็นที่จะเว้นระยะห่างเป็น x วินาทีคือ
โดย x ≥ 0 นอกนั้นจะเป็น 0 หมด
จะเห็นว่ารูปแบบการแจกแจงเข้าใจได้ง่าย คือลดลงเรื่อยๆแบบเลขชี้กำลัง
ส่วนฟังก์ชันแจกแจงความหนาแน่นสะสมก็จะบอกถึงความน่าจะเป็นในช่วงตั้งแต่ 0 ไปจนถึงค่านั้นๆ คำนวณได้จากปริพันธ์ของฟังก์ชันแจกแจงความหนาแน่น ได้เป็น
ที่จริงการคำนวณ FX(X) ควรต้องเริ่มจาก -∞ แต่เพราะค่าที่ x ติดลบนั้นเป็น 0 หมด จึงเริ่มจาก 0
หากนำมาวาดกราฟของ fX(X) และ FX(X) เทียบที่ค่า λ ต่างๆก็จะได้แบบนี้
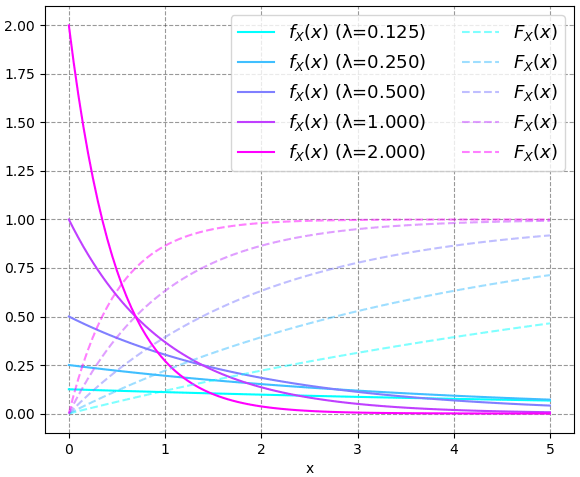
สำหรับกรณีนกบินในตัวอย่างตอนต้นบทนั้นนกแต่ละตัวเว้นช่วงกันโดยเฉลี่ย 10 วินาที ดังนั้น λ=1/10
ค่าคาดหมายและความแปรปรวนของการแจกแจงแบบเลขชี้กำลัง
ค่าความคาดหมาย ของการแจกแจงแบบเลขชี้กำลังคือ
ซึ่งก็มองภาพออกได้ไม่ยากว่าเป็นเพราะ λ คือจำนวนครั้งที่เหตุการณ์จะเกิดในหน่วยเวลาหนึ่ง ดังนั้นโดยเฉลี่ยแล้วระยะห่างระหว่างแต่ละครั้งก็ต้องเป็น 1/λ
ส่วนความแปรปรวนและส่วนเบี่ยงเบนมาตรฐานเป็น
นั่นคือส่วนเบี่ยงเบนมาตรฐานเองก็มีค่าเป็น 1/λ ซึ่งก็คือระยะห่างเฉลี่ยระหว่างเหตุการณ์แต่ละครั้ง
ความสัมพันธ์ระหว่างการแจกแจงแบบเลขชี้กำลังกับการแจกแจงปัวซง
การแจกแจงแบบเลขชี้กำลังมีความเกี่ยวพันกับการแจกแจงปัวซง ซึ่งได้เขียนถึงไปในบทที่ ๗
ความสัมพันธ์ระหว่างการแจกแจงแบบเลขชี้กำลังและการแจกแจงปัวซงนั้นมีลักษณะคล้ายความสัมพันธ์ระหว่าการแจกแจงทวินามและการแจกแจงปัวซง
ที่จริงแล้วการแจกแจงทั้งสองนั้นเกิดขึ้นพร้อมกันในสถานการณ์เดียวกัน แค่มองคนละสิ่งกัน
สมมุติว่าเรากำลังพิจารณาจำนวนคนเข้าเว็บในแต่ละวัน โดยพบว่าเฉลี่ยแล้ววันหนึ่งมีคนเข้าวันละ 12000 ครั้ง
ในที่นี้หากพิจารณาระยะเวลาที่เว้นระหว่างการเข้าแต่ละครั้งก็จะเป็นการแจกแจงแบบเลขชี้กำลัง
และหากแบ่งช่วงเวลาเป็นนาที (1 วันมี 24×60=1440 นาที) แล้วดูว่าแต่ละนาทีมีคนเข้ากี่คน จะได้การแจกแจงปัวซง
ลองเขียนโค้ดจำลองสถานการณ์ขึ้นดู เริ่มจากสุ่มค่าเวลาในหน่วยนาทีเป็นค่าต่อเนื่องตั้งแต่ 0 ถึง 1440 ออกมา 12000 ค่า ในแต่ละครั้งก็วาดเส้นแสดงเวลา พร้อมกับบันทึกว่าอยู่ในรอบไหน
import random
import matplotlib.pyplot as plt
n = 12000 # จำนวนรวม
t = 1440 # เวลาในหนึ่งวัน (นาที)
wela = []
chuang = [0]*t # ลิสต์นับจำนวนแต่ละช่วง
plt.figure(figsize=[6,2])
plt.xlim([0,t])
plt.yticks([])
for i in range(n):
w = random.uniform(0,t) # สุ่มเวลา
# วาดเส้นแสดงตำแหน่งเวลาที่สุ่มได้
plt.axvline(w,alpha=0.01,color='#8a3bc7')
wela += [w] # เก็บค่าเวลาที่สุ่มได้ครั้งนั้น
chuang[int(w)] += 1 # อยู่ในช่วงนาทีไหนก็บวกจำนวนช่วงนั้นไป
plt.show()จะได้รูปที่แสดงการกระจายตัวของเส้นเวลา 12000 เส้น ซึ่งค่อนข้างสม่ำเสมอ
จากนั้นใช้ Counter เพื่อนับว่ามีช่วงนาทีที่มีจำนวนครั้งที่เข้าเป็นแต่ละจำนวนอยู่เท่าไหร่
from collections import Counter
nap = Counter(chuang)
print(nap)ได้
Counter({7: 201, 8: 190, 9: 183, 6: 171, 10: 151, 5: 135, 11: 108, 12: 81, 4: 50, 13: 49, 3: 35, 14: 31, 15: 21, 2: 11, 16: 9, 17: 8, 1: 3, 21: 1, 20: 1, 18: 1})เมื่อวาดภาพก็จะได้การแจกแจงปัวซง
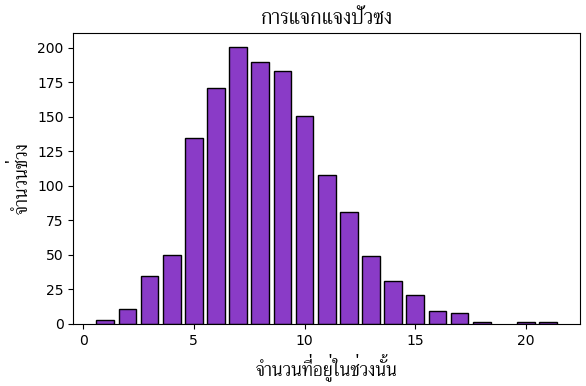
จากนั้นเรียงลำดับเวลาแล้วดูการแจกแจงของระยะเวลาเว้นช่วงก็จะได้การแจกแจงแบบเลขชี้กำลัง
wela = sorted(wela) # เรียงตามลำดับเวลา
wenwang = [] # ลิสต์เก็บระยะห่างแต่ละคู่
for i in range(1,n):
wenwang += [wela[i]-wela[i-1]] # เวลาลำดับที่ i ลบด้วยเวลาลำดับที่ i-1
plt.title('การแจกแจงแบบเลขชี้กำลัง',family='Tahoma',size=14)
plt.xlabel('ระยะห่างเวลา (นาที)',family='Tahoma',size=14)
plt.ylabel('จำนวนของแต่ละช่วง',family='Tahoma',size=14)
# วาดฮิสโทแกรม
plt.hist(wenwang,60,color='#8a3bc7',ec='#000000')
plt.show()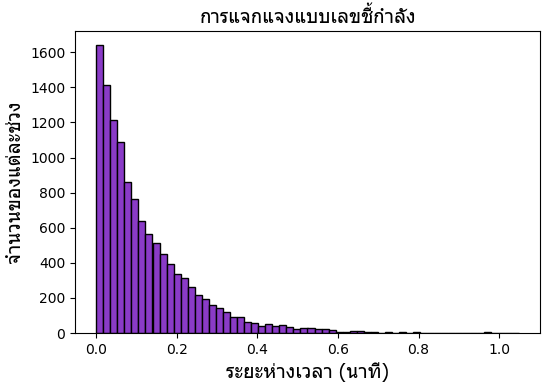
บทถัดไป >> บทที่ ๑๑