ต่อจาก บทที่ ๑๐

ในบทนี้จะว่าด้วยเรื่องของความน่าจะเป็นแบบเบย์ และนำไปสู่เรื่องของการแจกแจงเบตา ซึ่งเป็นการแจกแจงความน่าจะเป็นของค่าต่อเนื่องอีกแบบหนึ่ง




ความน่าจะเป็นที่เปลี่ยนแปลงไปตามวิธีคิดแบบเบย์

ก่อนที่จะเข้าเรื่องของการแจกแจงเบตาซึ่งเป็นหัวข้อหลัก ขอเริ่มอธิบายเรื่องความน่าจะเป็นแบบเบย์ ต่อจากที่ได้เขียนถึงไปในบทที่ ๓ โดยเริ่มจากยกตัวอย่าง

สมมุติว่าในโลกแฟนตาซีแห่งหนึ่งมีมังกรอยู่ 3 พันธุ์ ในที่นี้ขอตั้งชื่อว่าพันธุ์ α (อัลฟา), β (เบตา), γ (แกมมา) โดยที่สัดส่วนจำนวนเพศผู้กับเพศเมียต่างกันมาก คือ

• พันธุ์ α: เพศผู้ 75% เพศเมีย 25%
• พันธุ์ β: เพศผู้ 50% เพศเมีย 50%
• พันธุ์ γ: เพศผู้ 25% เพศเมีย 75%

วันหนึ่งนักเดินทางคนหนึ่งกำลังผจญภัยในหุบเขาแล้วไปเจอรังไข่ของมังกรซึ่งมีไข่อยู่หลายใบเข้าโดยไม่รู้ว่าเป็นมังกรพันธุ์อะไร แต่จู่ๆไข่ใบหนึ่งก็ฟักขึ้นมาเป็นมังกรเพศเมีย ถามว่าตัวนี้น่าจะมีความน่าจะเป็นที่จะเป็นมังกรพันธุ์ α,β,γ อยู่แค่ไหน

โดยสมมุติว่าเราไม่มีข้อมูลมาก่อนด้วยว่าแถวนี้มีโอกาสเจอพันธุ์ไหนมากกว่ากัน จึงถือว่ามีโอกาสเจอเท่ากันหมด และทั้งไข่และตัวอ่อนก็หน้าตาเหมือนกันจึงแยกพันธุ์ไม่ออก จึงได้แต่ตัดสินจากเพศของไข่ที่ออกมา

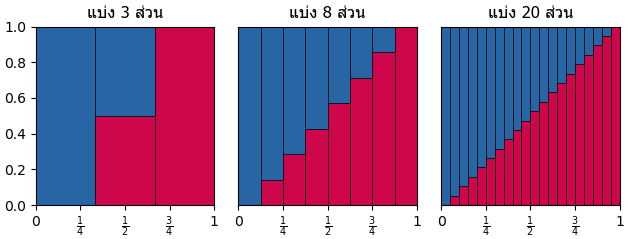
เริ่มจากลองวาดภาพแบ่งพื้นที่ความน่าจะเป็นดูเหมือนอย่างที่แสดงในบทที่ ๓

ตอนแรกเมื่อไม่มีข้อมูลอะไร โอกาสเป็นทั้ง 3 พันธุ์มีเท่ากัน อย่างละ 1/3 ดังนั้นแบ่งพื้นที่ออกเป็น 3 ส่วนเท่ากัน จากนั้นระบายสีตามสัดส่วนของเพศ โดยด้านบนสีน้ำเงินเป็นสัดส่วนของเพศผู้ ด้านล่างสีแดงเป็นของเพศเมีย สีแสดงถึงความน่าจะเป็นที่จะเจอเพศผู้หรือเพศเมีย



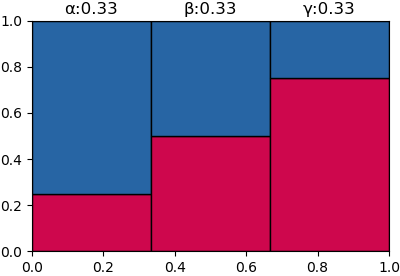
จากนั้นพอเราเห็นไข่มังกรออกมาเป็นเพศเมีย ก็ทำให้รู้แล้วว่าเป็นไปตามด้านล่าง ดังนั้นความน่าจะเป็นจึงกลายเป็น

• พันธุ์ α: 1/3×1/4 = 1/12
• พันธุ์ β: 1/3×1/2 = 1/6
• พันธุ์ γ: 1/3×3/4 = 1/4

พื้นที่รวมตอนนี้เหลือแค่ 0.5 ของพื้นที่เดิม จากนั้นปรับความน่าจะเป็นให้รวมกันเป็น 1 โดยหารด้วย 0.5 ก็จะได้

• พันธุ์ α: 1/6
• พันธุ์ β: 1/3
• พันธุ์ γ: 1/2

นำมาวาดภาพโดยปรับพื้นที่ใหม่ ตอนนี้ความน่าจะเป็นที่จะเป็นพันธุ์ γ เพิ่มขึ้นมาจนสูงสุด เพราะมีเพศเมียมากกว่า ส่วนความน่าจะเป็นที่จะเป็นพันธุ์ α ก็ต่ำลงมาก



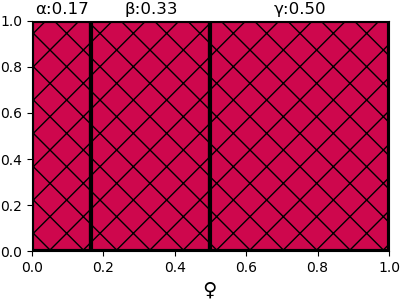
ตอนนี้ความน่าจะเป็นที่จะเป็นแต่ละพันธุ์ต่าไงจากเดิมแล้ว คราวนี้ถ้าหากมีไข่อีกใบฟักขึ้น ความน่าจะเป็นที่จะออกมาเป็นเพศผู้เพศเมียก็จะกลายเป็นแบ่งแบบนี้



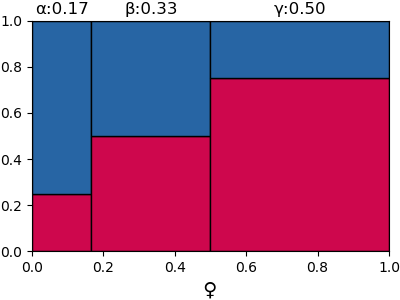
สมมุติว่าใบที่ 2 ฟักได้เพศผู้ คราวนี้ก็เขียนแบ่งพื้นที่ใหม่ตามสัดส่วนของพื้นที่ส่วนสีน้ำเงิน ตอนนี้กลายเป็นว่ามีเพศผู้เพศเมียอย่างละตัวแล้ว พันธุ์ β จึงมีความน่าจะเป็นมากสุดเพราะเป็นพันธุ์ที่มีเพศผู้กับเพศเมียเท่ากัน



ความน่าจะเป็นที่ใบต่อไปจะเป็นเพศผู้หรือเพศเมียก็เปลี่ยนไปอีก ความน่าจะเป็นของใบที่ 3 จะเป็นแบบนี้



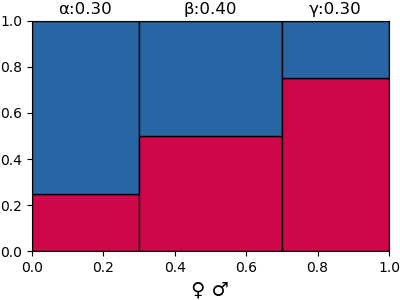
สมมุติว่าใบที่ 3 นี้ออกมาเป็นเพศผู้อีก คราวนี้จะกลายเป็นความน่าจะเป็นของพันธุ์ α สูงสุดแทน



พิจารณาความน่าจะเป็นของใบที่ 4 ต่อไปก็เป็นแบบนี้



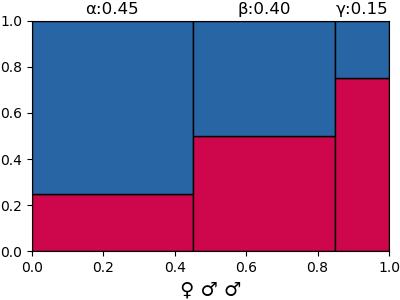
สมมุติว่าครั้งที่ 4 นี้ออกมาเป็นตัวเมีย



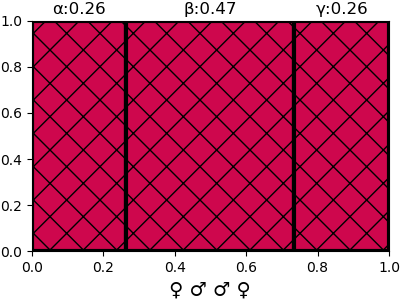
ดูใบที่ 5 ต่อไป



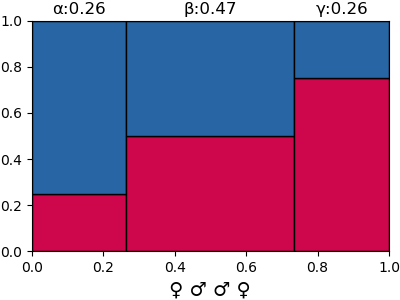
สมมุติว่าครั้งที่ 5 นี้เป็นเพศเมียอีกแล้ว ความน่าจะเป็นก็เปลี่ยนไปเป็นแบบนี้



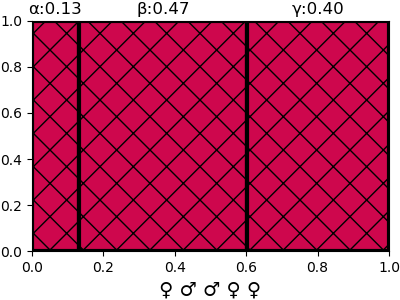
ดูความน่าจะเป็นของใบที่ 6 ต่อก็จะได้



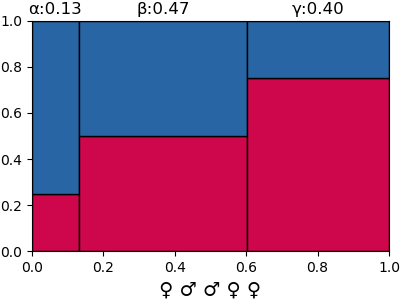
สมมุติว่าตัวที่ 6 ฟักออกมาเป็นเพศเมียอีก ความน่าจะเป็นของก็จะกลายเป็นแบบนี้



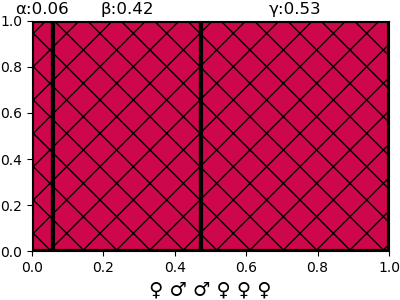
แล้วก็ทำอย่างนี้ซ้ำๆไปเรื่อยๆเมื่อมีไข่มังกรฟักขึ้นมาอีก

จะเห็นว่าความน่าจะเป็นเปลี่ยนไปเรื่อยๆตามข้อมูลที่เรามีอยู่ สิ่งที่เรารู้นั้นเปลี่ยนแปลงความน่าจะเป็นจากที่มีอยู่เดิม นี่คือหลักการความน่าจะเป็นของเบย์

อาจลองเขียนโปรแกรมไพธอนจำลองสถานการณ์ได้ดังนี้

# โอกาสที่จะได้เพศเมียของแต่ละพันธุ์
m = {'α':1/4,
     'β':1/2,
     'γ':3/4}

# ความน่าจะเป็นตั้งต้น
p = {'α':1/3,
     'β':1/3,
     'γ':1/3}

# เพศของไข่ที่ฟักออกมาตามลำดับ
khai = [1,0,0,1,1,1] # 0 เพศผู้, 1 เพศเมีย
for i in range(len(khai)):
    # ปรับค่าความน่าจะเป็นใหม่โดยแยกกรณีตามผลที่ได้ว่าเป็นเพศไหน
    if(khai[i]==1): # กรณีได้เพศเมีย
        p['α'] = p['α']*m['α']
        p['β'] = p['β']*m['β']
        p['γ'] = p['γ']*m['γ']
    else: # กรณีได้เพศผู้
        p['α'] = p['α']*(1-m['α'])
        p['β'] = p['β']*(1-m['β'])
        p['γ'] = p['γ']*(1-m['γ'])
    
    ppp = p['α']+p['β']+p['γ'] # ผลรวมใหม่หลังแบ่งใหม่
    # ปรับความน่าจะเป็นให้รวมกันได้ 1
    p['α'] /= ppp
    p['β'] /= ppp
    p['γ'] /= ppp
    print(p) # แสดงความน่าจะเป็นใหม่หลังปรับแล้วในแต่ละรอบ

ได้

{'α': 0.16666666666666666, 'β': 0.3333333333333333, 'γ': 0.5}
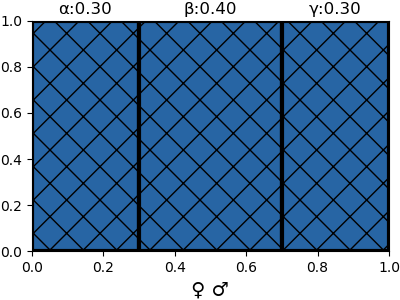
{'α': 0.30000000000000004, 'β': 0.4, 'γ': 0.30000000000000004}
{'α': 0.45000000000000007, 'β': 0.4, 'γ': 0.15000000000000002}
{'α': 0.2647058823529412, 'β': 0.47058823529411764, 'γ': 0.2647058823529412}
{'α': 0.1323529411764706, 'β': 0.47058823529411764, 'γ': 0.3970588235294118}
{'α': 0.05844155844155844, 'β': 0.4155844155844156, 'γ': 0.5259740259740261}

ผลจากตรงนี้สามารถเอาไปวาดเป็นภาพแบ่งพื้นที่ได้เป็นไปตามภาพข้างบน




ความน่าจะเป็นของความน่าจะเป็น

จากตัวอย่างเรื่องมังกรที่ยกมาข้างต้นนั้นจะเห็นความน่าจะเป็นที่จะได้เพศไหนเปลี่ยนไปตามพันธุ์ของมังกร พอดูผลที่ได้ว่าเป็นเพศไหนก็ทำให้ความน่าจะเป็นที่จะเป็นพันธุ์ไหนเปลี่ยนไปอีก แล้วก็ทำให้ความน่าจะเป็นที่จะเป็นแต่ละเพศเปลี่ยนไปด้วย

อย่างไรก็ตาม ตัวอย่างข้างต้นนี้เป็นกรณีที่เรามีรูปแบบของคำตอบเตรียมไว้ในใจอยู่แล้ว คือตั้งต้นมาก็รู้ว่ามีมังกร 3 พันธุ์ที่มีลักษณะแบบนี้

แต่ปัญหาในชีวิตจริงส่วนใหญ่แล้วมักไม่ได้มีตัวเลือกคำตอบอย่างจำกัดแบบนี้ เช่นถ้ามังกรสามารถมีความน่าจะเป็นเพศผู้หรือเพศเมียมากแค่ไหนก็เป็นไปได้เราก็ไม่รู้อะไรมาก่อน แบบนั้นก็อาจจะพิจารณาว่าถ้ามีความน่าจะเป็นอยู่เท่าไหร่จะมีโอกาสได้เพศผู้เพศเมียมากแค่ไหน

แต่จริงๆแล้วความน่าจะเป็นเป็นค่าใดๆก็ได้ เป็นค่าแบบต่อเนื่อง ถ้าจะแบ่งจริงๆก็ควรจะได้เป็นอนันต์ส่วน ดังนั้นถ้าจะแบ่งจริงๆก็จะต้องแยกคิดเป็นอนันต์กรณี ลองนึกภาพว่าค่อยๆแบ่งย่อยละเอียดขึ้นไปเรื่อยๆแบบนี้ จนเข้าใกล้อนันต์ส่วน



เมื่อลองมาคิดปัญหาเดิมเรื่องเพศของมังกรใหม่ แค่คราวนี้ไม่แบ่งเป็นพันธุ์ α β γ แล้วแต่มองว่าความน่าจะเป็นที่สัดส่วนเพศผู้เพศเมียจะเป็นเท่าไหร่นั้นมีค่าเท่าไหร่

วิธีการคำนวณอาจจะทำแบบเดียวกับตัวอย่างที่แล้วที่แบ่งเป็น 3 ส่วน โดยคราวนี้แบ่งกรณีความน่าจะเป็นออกเยอะๆเป็นหลายๆค่า

แต่การจะแบ่งคิดเป็นอนันต์แบบนั้นย่อมเป็นไปไม่ได้ แต่เราสามารถจำลองให้เห็นภาพใกล้เคียงโดยใช้การแบ่งเป็นจำนวนเยอะๆ

ในที่นี้ขอแสดงตัวอย่างโดยแบ่งค่าความน่าจะเป็นออกเป็น 0,0.01,0.02,...0.99,1 ทั้งหมด 101 ส่วน

หากลองคิดเหมือนตัวอย่างด้านบน แค่เปลี่ยนเป็นแบ่ง 101 ส่วนตามนี้ อาจเขียนโค้ดจำลองกรณีนี้ได้ดังนี้

n = 100 # จำนวนขีดที่จะแบ่ง
m = [i/n for i in range(n+1)] # สัดส่วนที่จะเป็นเพศเมียของแต่ละตัว
p = [1/(n+1)]*(n+1) # ความน่าจะเป็นตั้งต้นทั้ง 101 ตัว เริ่มแรกให้เท่ากันหมด โดยหารตามจำนวนช่วงที่แบ่ง เป็น 1/101

# เพศของไข่ที่ฟักออกมาตามลำดับ (ให้เหมือนตัวอย่างด้านบน)
khai = [1,0,0,1,1,1]
for i in range(len(khai)):
    # ไล่ปรับค่าความน่าจะเป็นของแต่ละกรณีไปตามผลที่ได้
    for t in range(n+1):
        if(khai[i]==1): # ถ้าได้เพศเมีย
            p[t] = p[t]*m[t]
        else: # ถ้าได้เพศผู้
            p[t] = p[t]*(1-m[t])
    
    p_ruam = sum(p) # รวมความน่าจะเป็นใหม่
    # หารด้วยความน่าจะเป็นรวมเพื่อให้รวมเป็น 1 เหมือนเดิม
    for t in range(n+1):
        p[t] /= p_ruam
    print(p) # แสดงความน่าจะเป็นหลังจากปรับแต่ละรอบ

ผลที่ได้แต่ละรอบจะได้ลิสต์ที่มีตัวเลขแสดงค่าความน่าจะเป็นของทั้ง 101 กรณี ซึ่งเปลี่ยนไปเรื่อยๆในแต่ละรอบ ในที่นี้ขอละไว้ไม่แสดงผลเพราะยาวมาก แต่จะขอเอามาวาดเป็นกราฟแทน

หากเอาผลที่ได้มาวาดเป็นกราฟแสดงการแจกแจงความหนาแน่นของความน่าจะเป็น โดยให้แนวนอนเป็นค่าอัตราส่วนที่เป็นเพศเมีย แนวตั้งคือความน่าจะเป็นที่จะเป็นอัตราส่วนเท่านั้น ดังนั้นเริ่มแรกยังไม่รู้อะไรถือว่าความน่าจะเป็นที่จะเป็นแต่ละเพศมีค่าเท่ากันหมด แต่เมื่อตัวแรกออกมาเป็นเพศเมียก็จะวาดกราฟได้เป็นแบบนี้



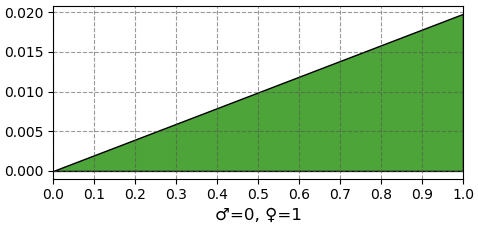
ซึ่งก็สมเหตุสมผลว่าในเมื่อผลตัวแรกออกมาเป็นเพศเมีย หมายความว่าความน่าจะเป็นที่นี่จะเป็นมังกรที่มีสัดส่วนเพศเมียมากก็มากกว่า กราฟจึงเอียงไปทางนี้

หลังจากนั้นถ้าไข่ใบที่ 2 ออกมาเป็นเพศผู้ ความน่าจะเป็นก็กลายมาเป็นแบบนี้



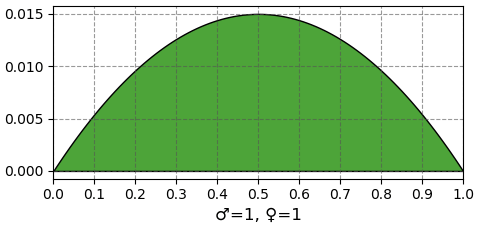
หลังจากใบที่ 3 ออกมาเป็นเพศผู้



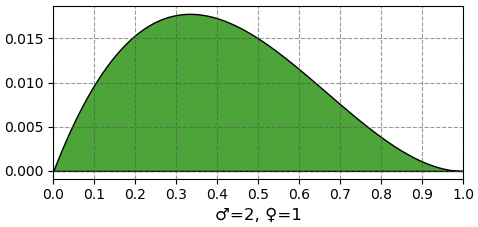
หลังจากใบที่ 4 ออกมาเป็นเพศเมีย



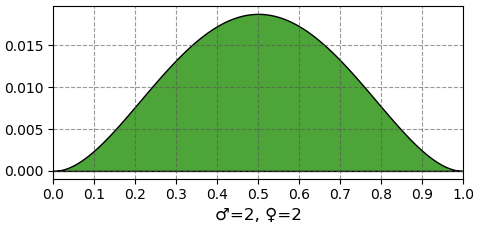
หลังจากใบที่ 5 ออกมาเป็นเพศเมีย



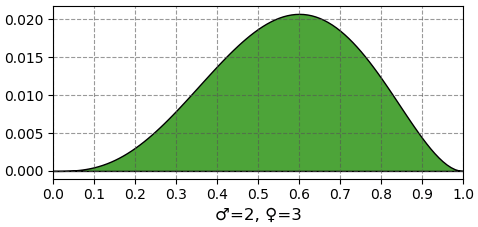
หลังจากใบที่ 6 ออกมาเป็นเพศเมีย



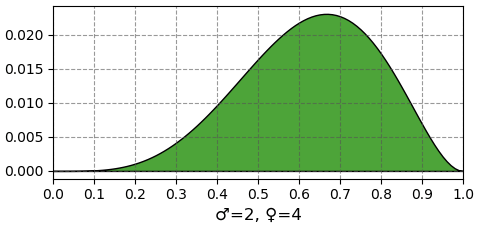
จะเห็นกราฟการแจกแจงความน่าจะเป็นของแต่ละกรณีความน่าจะเป็นซึ่งเปลี่ยนไปเรื่อยๆตามข้อมูลที่มีในแต่ละขั้นหลังจากที่เห็นผลแต่ละครั้ง

การแจกแจงที่ได้ตามตัวอย่างนี้เป็นลักษณะของการแจกแจงแจงเบตา (beta distribution)




การแจกแจงเบตา

เมื่อเราพิจารณาถึงเหตุการณ์บางอย่างที่ไม่รู้ว่ามีความน่าจะเป็นอยู่เท่าไหร่ โดยดูจากผลลัพธ์ที่ออกมาโดยพิจารณาตามแนวคิดแบบเบย์ ความน่าจะเป็นที่จะมีความน่าจะเป็นเป็นค่านั้นๆจะมีลักษณะการแจกแจงเป็นฟังก์ชันเบตา

โดยเราจะได้ฟังก์ชันความหนาแน่นของความน่าจะเป็นของความน่าจะเป็นเป็นดังนี้


โดยที่ α-1 แทนจำนวนครั้งที่เกิดเหตุการณ์ที่พิจารณาขึ้นสำเร็จ และ β-1 แทนจำนวนครั้งที่เหตุการณ์ตามที่พิจารณานั้นเกิดขึ้นไม่สำเร็จ จากการทำการทดลอง (α-1)+(β-1) ครั้ง

หรือจะเปลี่ยนจากสำเร็จและล้มเหลวเป็นใช้คำว่าเป็นผลบวกกับผลลบก็ได้ หากเทียบกับในตัวอย่างเรื่องมังกรข้างต้นนี้ α-1 คือจำนวนครั้งที่มังกรออกมาเป็นเพศเมีย ส่วน β-1 คือจำนวนครั้งที่ได้มังกรเพศผู้

* อนึ่ง ให้ระวังว่าสูตรการแจกแจงได้กำหนดให้จำนวนครั้งเป็น α-1, β-1 ไม่ใช่เป็น α, β ดังนั้นเมื่อเริ่มต้นแรกสุดจำนวนทดลองเป็น 0 ครั้งก็จะเป็น α=1, β=1 ไม่ได้เริ่มที่ 0

* และที่จริงแล้วค่าของ α,β ในการแจกแจงเบตานั้นอาจไม่จำเป็นต้องเป็นจำนวนเต็ม แต่ในที่นี้จะขอพิจารณาในกรณีแค่เป็นจำนวนเต็ม เพราะในที่นี้ α-1 และ β-1 แทนจำนวนครั้ง ซึ่งเป็นจำนวนเต็มอยู่แล้ว

ส่วน B(α,β) ในที่นี้คือฟังก์ชันเบตา ซึ่งเป็นค่าคงตัวที่ขึ้นกับค่าของห α และ β

ค่าของฟังก์ชันเบตาเมื่อ α และ β เป็นจำนวนเต็ม ฟังก์ชันเบตาจะคำนวณได้ว่า


หากลองวาดกราฟการแจกแจงเบตาที่ค่า α และ β ต่างๆจะได้เป็นลักษณะดังนี้



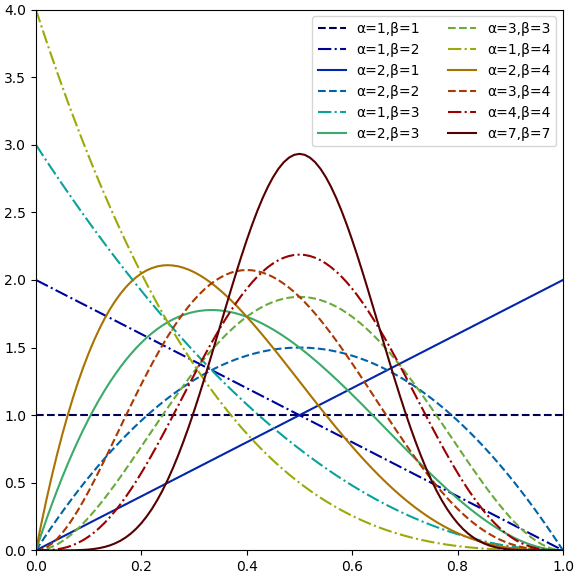
กรณี α=1,β=1 หมายถึงยังไม่ได้เริ่มทดลองอะไรไป กราฟจะเป็นเส้นตรงอยู่ที่ 1 คือทุกค่ามีโอกาสเท่ากันหมด

แต่เมื่อทดลองไปแล้ว 1 ครั้ง สำเร็จ 1 ครั้งก็จะได้ α=2,β=1 ก็เป็นกราฟเส้นตรงที่ไล่จาก 0 ขึ้นไป ในทางกลับกันถ้าล้มเหลวก็จะเป็น α=1,β=2 เป็นกราฟเส้นตรงที่เฉียงไปอีกทาง

จุดสูงสุดของกราฟจะเป็นไปตามสัดส่วนของจำนวนครั้งที่ได้กับไม่ได้ เช่นถ้าทำ 3 ครั้ง ได้ 1 ครั้ง จุดสูงสุดก็ต้องอยู่ที่ 1/3 ถ้าได้ 2 ครั้งก็จะอยู่ที่ 2/3 เป็นต้น

นั่นคือจุดสูงสุดสามารถคำนวณได้จากค่า α,β เป็นดังนี้


จะเห็นว่ากรณีที่ผลได้ตามที่ต้องการและไม่ต้องการเป็นจำนวนเท่ากัน เช่น α=β=2, α=β=3 ค่าสูงสุดจะอยู่ตรงกลางของกราฟ แสดงว่าโอกาสที่ความน่าจะเป็นนั้นจะเป็น 0.5 มีมากที่สุด แต่การแจกแจงก็ต่างกันไป ยิ่ง α และ β ยิ่งไปกองอยู่ตรงกลางๆมากขึ้น

ส่วนค่าคาดหมายของการแจกแจงเบตาจะคำนวณได้เป็น





ว่าด้วยเรื่องการแจกแจงความน่าจะเป็นตั้งต้น

แนวคิดเรื่องความน่าจะเป็นแบบเบย์นั้นจะพิจารณาถึงเรื่องของความน่าจะเป็นก่อนหน้าและความน่าจะเป็นภายหลัง

ความน่าจะเป็นก่อนหน้าก็คือความน่าจะเป็นที่เรามีอยู่เดิมแล้วก่อนที่จะเริ่มทำการทดลอง

ซึ่งในตัวอย่างที่ผ่านมา ตอนแรกเริ่มไม่มีข้อมูลอะไรเลย จึงมองว่าการแจกแจงความน่าจะเป็นอยู่ที่ 1 เท่ากันทั้งหมด โดยทั่วไปสามารถมองได้ว่าเป็นการคาดการณ์ตั้งต้นที่ดูสมเหตุสมผลที่สุด

แต่จริงๆแล้วความน่าจะเป็นตั้งต้นนี้แล้วแต่คนกำหนด ซึ่งก็ไม่จำเป็นต้องเริ่มจากเท่ากันหมดแบบนั้นเสมอไป หากเรามีข้อมูลบางอย่างที่ทำให้คิดว่าความน่าจะเป็นโน้มเอียงไปในทางค่อนข้างมาก การแจกแจงเริ่มต้นก็อาจเริ่มเอียงไปทางฝั่งขวาก่อนก็ได้ ซึ่งการคำนวณก็จะต่างไป

แต่การที่การแจกแจงความน่าจะเป็นจะออกมาในรูปของการแจกแจงเบตาแบบนี้ ความน่าจะเป็นตั้งต้นเองก็ต้องเริ่มจากการแจกแจงเบตา ซึ่งค่าที่แจกแจงเป็น 1 เท่ากันหมดก็คือกรณี α=1,β=1 เป็นการแจกแจงเบตารูปแบบหนึ่งอยู่แล้ว

เมื่อทำการทดลองเพิ่มขึ้น การแจกแจงที่เปลี่ยนไปตามการทดลองแต่ละครั้งก็ยังคงเป็นฟังก์ชันเบตา โดยค่า α หรือ β ก็จะเพิ่มขึ้นไปเรื่อยๆตามจำนวนครั้งที่สำเร็จและล้มเหลว

ดังนั้นการเริ่มต้นแจกแจงความน่าจะเป็นเท่ากันหมดแบบนี้นอกจากจะคิดง่ายแล้วก็ยังทำให้การแจกแจงหลังจากนั้นเป็นไปตามการแจกแจงเบตา

นอกจากนี้แล้ว แม้จะไม่กำหนดการแจกแจงความน่าจะเป็นตั้งต้นแบบเท่ากันหมด เราก็อาจกำหนดเป็นการแจกแจงเบตาที่ค่าเริ่มต้นที่ไม่ใช่ α=1,β=1 ก็ได้

เช่นถ้าเดิมทีคิดว่าความน่าจะเป็นที่จะสำเร็จได้ควรจะมากกว่าอยู่แล้ว อาจเริ่มจาก α=2,β=1 หรือถ้าคิดว่าโอกาสไม่ได้มากกว่าก็อาจเริ่มจาก α=1,β=2 ซึ่งก็จะเทียบเท่ากับความน่าจะเป็นในกรณีที่ทดลองไปแล้ว 1 ครั้ง แม้ว่าจริงๆเราจะยังไม่เริ่มทดลอง

หรือถ้ามองว่าความน่าจะเป็นที่จะได้กับไม่ได้นั้นควรจะมีพอๆกันอยู่แล้ว ยังไงคงไม่มีทางที่จะเป็น 0 หรือ 1 ไปได้ แบบนั้นอาจเริ่มที่ α=2,β=2 ซึ่งมีค่าสูงสุดที่ 0.5

จากตัวอย่างที่ยกมานี้ ทำให้เห็นภาพได้ชัดขึ้นว่าหลักความน่าจะเป็นแบบเบย์นั้นดูเป็นอะไรที่ขึ้นกับมุมมองของคน โดยขึ้นอยู่กับประสบการณ์และข้อมูลที่มี การแจกแจงความน่าจะเป็นตั้งต้นมีผลต่อผลการคำนวณต่อๆไป

ซึ่งตรงนี้จึงทำให้ผู้ที่ไม่เห็นด้วยกับแนวคิดความน่าจะเป็นแบบเบย์มองว่าดูเป็นอะไรที่เลื่อนลอย คลุมเครือ

อย่างไรก็ตาม ก็เป็นความจริงที่ว่าแนวคิดความน่าจะเป็นแบบเบย์นั้นถูกใช้เพื่อสรุปผลการทดลองทางวิทยาศาสตร์ได้อย่างสมเหตุสมผลมาแล้วมากมาย

คนเราวิเคราะห์ความเป็นไปได้ของสิ่งต่างๆจากข้อมูลที่ตัวเองมีอยู่ ยิ่งมีข้อมูลมากก็ยิ่งจะทำนายได้แม่นยำมากขึ้น ในโลกยุคที่เราสามารถค้นข้อมูลข่าวสารมาวิเคราะห์ได้ง่ายเช่นตอนนี้ หลักความน่าจะเป็นแบบเบย์จึงได้ย่ิงแสดงผลงานให้เห็น และผู้คนก็มองเห็นความสำคัญมากยิ่งขึ้น




บทถัดไป >> บทที่ ๑๒

~ เกี่ยวกับเรา ~

สารบัญ

รวมคำแปลวลีเด็ดจากญี่ปุ่น

ภาษา python มอดูลต่างๆ -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch การเรียนรู้ของเครื่อง -- โครงข่าย      ประสาทเทียม

ภาษา javascript

ภาษา mongol

ภาษาศาสตร์

maya

ความน่าจะเป็น

บันทึกในญี่ปุ่น

บันทึกในจีน -- บันทึกในปักกิ่ง -- บันทึกในฮ่องกง -- บันทึกในมาเก๊า

บันทึกในไต้หวัน

บันทึกในยุโรปเหนือ

บันทึกในประเทศอื่นๆ

qiita

บทความอื่นๆ

บทความแบ่งตามหมวด

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --sql --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา บันทึก เรื่องแต่ง ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม

　 ค้นหาบทความ

　 บทความล่าสุด

　 บทความแนะนำ

บทความแต่ละเดือน

ค้นบทความเก่ากว่านั้น

ไทย

日本語

中文