opencv-python เบื้องต้น บทที่ ๑๖: การแบ่งเขตภาพโดยพิจารณาส่วนที่เชื่อมต่อกัน
เขียนเมื่อ 2020/06/28 19:15
แก้ไขล่าสุด 2024/02/22 10:23
ต่อจาก บทที่ ๑๕
นอกจากการตีกรอบโดยใช้เส้นเค้าโครงดังที่ได้เขียนถึงไปใน ๓ บทที่ผ่านมาแล้ว อีกวิธีที่ใช้ในการแบ่งเขตของภาพก็คือการติดป้ายหมายเลขบอกว่าจุดไหนคือส่วนของเขตไหน ซึ่งเป็นวิธีที่จะแนะนำในบทนี้
การแบ่งกลุ่มก้อนในภาพโดยแสดงเป็นหมายเลข
ใน opencv มีฟังก์ชัน cv2.connectedComponents() ซึ่งเอาไว้แบ่งเขตของภาพแล้วแปลงออกมาเป็นตัวเลขที่แสดงบอกว่าตรงจุดไหนเป็นส่วนของหมายเลขที่เท่าไหร่
วิธีใช้ใกล้เคียงกับ cv2.findContours() คือใช้กับภาพที่เป็นขาวดำ โดยฟังก์ชันนี้จะถือว่าค่า 0 (สีดำ) เป็นฉากหลัง และที่เหลือเป็นวัตถุ
ค่าที่ต้องใส่ในฟังก์ชันนี้มีแค่ตัวอาเรย์รูปภาพเท่านั้น จึงใช้ค่อนข้างง่าย
ค่าคืนกลับของฟังก์ชันนี้มี ๒ ตัว ตัวแรกคือจำนวนเขตที่แบ่งได้ ส่วนตัวหลังคือค่าตัวเลขที่แสดงว่าส่วนไหนเป็นของหมายเลขอะไร
ลองดูตัวอย่างการใช้ โดยเอาภาพมาตัดค่าเป็นขาวดำด้วย cv2.threshold() แล้วจึงใช้ cv2.connectedComponents() จากนั้นวาดผลลัพธ์ที่ได้ดู

rin16c01.jpg
import cv2
import numpy as np
import matplotlib.pyplot as plt
rin = cv2.imread('rin16c01.jpg') # อ่านภาพสี
# คัดแยกส่วนฉากหลัง
_,thresh = cv2.threshold(cv2.cvtColor(rin,cv2.COLOR_BGR2GRAY),10,255,0)
# ทำการแบ่งส่วน
n,lek = cv2.connectedComponents(thresh)
# แสดงผลการแบ่งส่วน
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()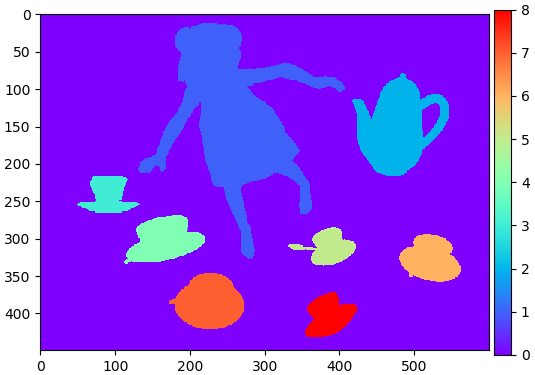
จะได้ค่าตัวเลขไล่ตั้งแต่ 0 ถึง 8 โดยฉากหลังจะเป็นค่า 0 แล้วก็ไล่ 1,2,3,... ไปตามลำดับ เรียงตามตำแหน่งที่เริ่มปรากฏ
การแบ่งกลุ่มก้อนพร้อมเอาข้อมูลของแต่ละกลุ่ม
ฟังก์ชัน cv2.connectedComponents() นั้นจะให้ข้อมูลแค่ว่าตำแหน่งไหนเป็นหมายเลขอะไร แต่ถ้าอยากได้ข้อมูลเพิ่มเติมมากกว่านี้ไปในขณะเดียวกันก็อาจใช้ฟังก์ชัน cv2.connectedComponentsWithStats()
วิธีใช้เหมือนกันกับ cv2.connectedComponents() แต่จะคืนค่าออกมา ๔ ตัว โดย ๒ ตัวแรกจะเหมือนกับใน cv2.connectedComponents() แต่เพิ่มมาอีก ๒ ตัวคือ
ตัวที่ ๓ เป็นข้อมูลที่บอกตำแหน่งขอบเขตของกลุ่ม โดยเขียนเป็น [x ซ้ายสุด, y บนสุด, ความกว้าง, ความสูง, พื้นที่รวม]
ตัวที่ ๔ แสดงตำแหน่ง x,y ของจุดเซ็นทรอยด์ของกลุ่ม
ตัวอย่าง ลองทำเหมือนภาพที่แล้ว แค่เปลี่ยนเป็นใช้ฟังก์ชัน cv2.connectedComponentsWithStats() แทน

gumi16c01.jpg
gumi = cv2.imread('gumi16c01.jpg')
_,thresh = cv2.threshold(cv2.cvtColor(gumi,cv2.COLOR_BGR2GRAY),15,255,0)
n,lek,stat,centroid = cv2.connectedComponentsWithStats(thresh)
print(stat)
print(centroid)ได้
[[ 0 0 600 450 209571]
[ 115 2 303 318 28451]
[ 38 105 79 167 7211]
[ 431 158 125 94 7038]
[ 143 226 60 88 3000]
[ 134 330 105 83 3980]
[ 300 331 112 110 6120]
[ 442 344 101 74 4629]]
[[304.95781859 224.22485458]
[255.3485642 147.80011247]
[ 72.01941478 204.67799196]
[491.31713555 210.42909918]
[173.482 273.263 ]
[192. 372.67060302]
[352.22957516 388.49803922]
[490.88139987 384.82458414]]ลองวาดภาพแสดงผลที่ได้พร้อมแสดงตำแหน่งเซ็นทรอยด์
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.scatter(centroid[:,0],centroid[:,1],c='k')
plt.show()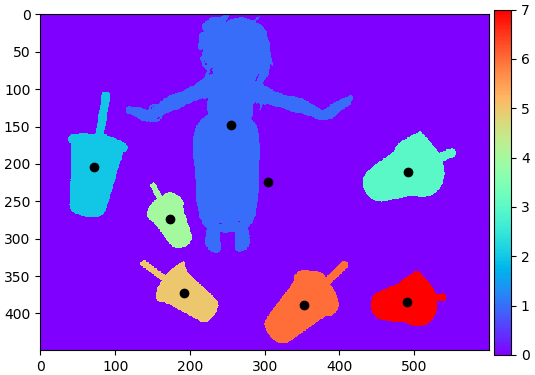
เอาตำแหน่งขอบเขตของภาพที่ได้ใช้ตีกรอบสี่เหลี่ยมล้อม พร้อมทั้งแสดงค่าพื้นที่ไว้ที่จุดเซ็นทรอยด์
ax = plt.axes()
plt.imshow(lek,cmap='rainbow')
for (x,y,w,h,a),(cx,cy) in zip(stat,centroid):
ax.add_patch(plt.Rectangle((x,y),w,h,fill=False,ec='k',lw=2,ls=':'))
plt.text(cx,cy,a,ha='center',color='k')
plt.tight_layout()
plt.show()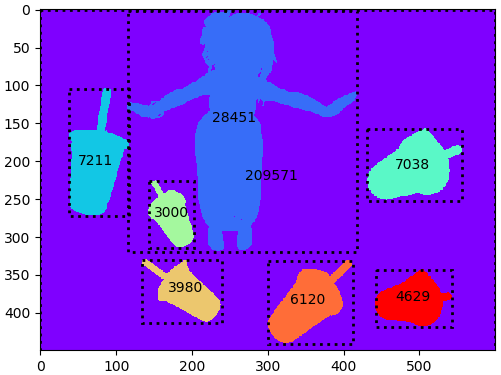
การหาความลึกของแต่ละส่วนในภาพ
นอกจากแบ่งเขตของภาพเพื่อแยกเอาตัววัตถุแล้ว ข้อมูลอีกอย่างที่สำคัญซึ่งอาจใช้บ่อยก็คือจุดไหนลึกเข้ามาในตัววัตถุมากแค่ไหน
ฟังก์ชัน cv2.distanceTransform() จะคำนวณหาความลึก (ระยะห่างต่ำสุดจากขอบนอก) ของแต่ละจุดภายในวัตถุในภาพ
ค่าที่ต้องใส่ในฟังก์ชันนี้คือ src, distanceType, markSize ตามลำดับ
distanceType คือชนิดวิธีวัดระยะห่าง ใส่เป็นแฟล็ก โดยทั่วไปจะใช้ cv2.DIST_L2 คือระยะทางแบบยุคลิดธรรมดา
ส่วน markSize อาจใส่เป็น 0, 3 หรือ 5
ตัวอย่างการใช้

teto16c01.jpg
teto = cv2.imread('teto16c01.jpg')
_,thresh = cv2.threshold(cv2.cvtColor(teto,cv2.COLOR_BGR2GRAY),5,255,0)
n,lek = cv2.connectedComponents(thresh)
dist = cv2.distanceTransform(thresh,cv2.DIST_L2,0)
plt.figure(figsize=[6,8.5])
plt.subplot(211)
plt.imshow(lek>0,cmap='copper')
plt.subplot(212)
plt.imshow(dist,cmap='jet')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()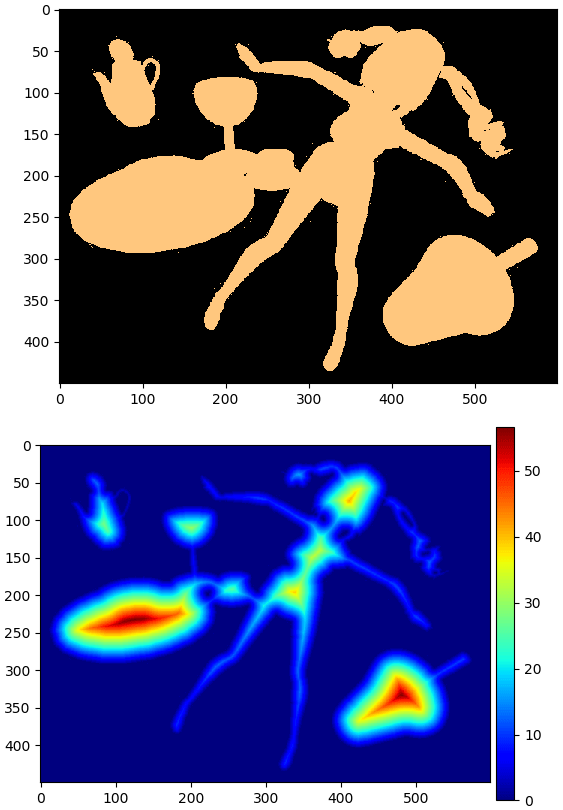
แบ่งเขตภาพด้วยวิธีการแบ่งสันปันน้ำ
ต่อไปจะแนะนำการใช้ฟังก์ชัน cv2.watershed() ซึ่งเป็นวิธีการหนึ่งที่ช่วยในการแบ่งเขตกลุ่มก้อนภายในภาพ
watershed แปลว่า "สันปันน้ำ" คือส่วนสันส่วนยอดของเทือกเขาที่เวลาฝนตกน้ำจะไหลแยกไปคนละฟากของเทือกเขาโดยมีสันตรงนี้เป็นจุดแบ่ง สันปันน้ำมักถูกใช้เป็นตัวแบ่งชายแดนระหว่างเขตหรือประเทศ
ภาพประกอบคือแนวสันปันน้ำบนเทือกเขาพนมดงรักบริเวณเขาพระวิหาร เส้นสีแดงคือสันปันน้ำ ลูกศรชี้ทิศทางการไหลของน้ำเมื่อฝนตกบนนี้ ด้านบนคือเขตประเทศไทย ด้านล่างคือกัมพูชา ตัวปราสาทอยู่ฝั่งไทยเมื่อแบ่งด้วยสันปันน้ำ
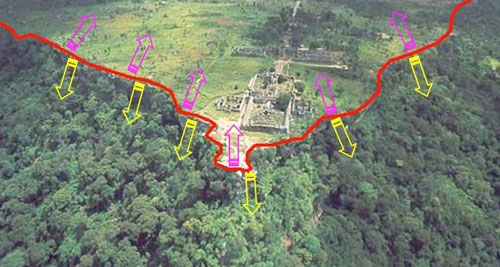
(ที่มาของภาพ)
แนวคิดตรงนี้เป็นที่มาของอัลกอริธึมสำหรับแบ่งเขตภาพ โดยใช้แนวคิดของสันปันน้ำในลักษณะเช่นนี้
ขอเริ่มอธิบายจากการยกตัวอย่างภาพที่เป็นปัญหาที่อาจต้องใช้ เช่นมีภาพแบบนี้ แล้วต้องการแบ่งบริเวณเพื่อแยกของชิ้นต่างๆออกจากกัน แต่ปัญหาคือมีบางส่วนที่เชื่อมติดกันอยู่

miku16c01.jpg
เอามาแบ่งด้วย cv2.connectedComponents() ดูเหมือนตัวอย่างอื่นๆข้างบน
miku = cv2.imread('miku16c01.jpg')
_,thresh = cv2.threshold(cv2.cvtColor(miku,cv2.COLOR_BGR2GRAY),10,255,0)
n,lek = cv2.connectedComponents(thresh)
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()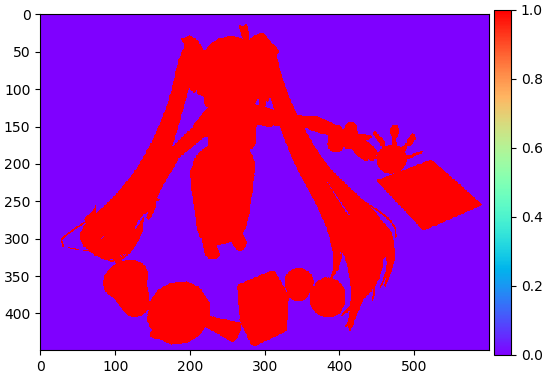
ผลที่ได้จะเห็นว่าแบ่งแล่้วได้เป็นบริเวณเดียวกันไปหมด เนื่องจากว่าแต่ละส่วนมีบริเวณที่เชื่อมติดกันอยู่เล็กน้อย
เพื่อที่จะกำจัดส่วนที่เชื่อมกัน อาจใช้ cv2.distanceTransform() เพื่อดูว่าส่วนไหนลึกจากขอบแค่ไหน
khwamluek = cv2.distanceTransform(thresh,cv2.DIST_L2,0)
plt.imshow(khwamluek,cmap='plasma')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()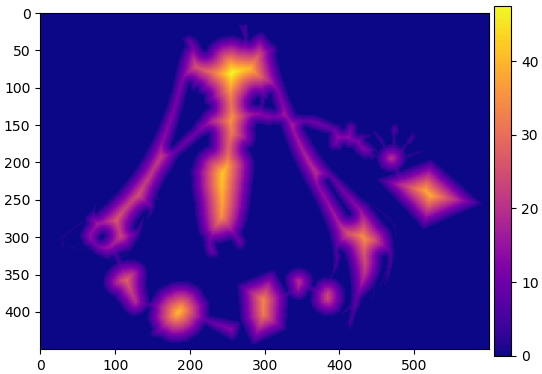
จากนั้นก็คัดเอาเฉพาะส่วนที่ห่างจากขอบมากพอเพื่อถือว่าเป็นส่วนที่แน่นอนว่าเป็นวัตถุ ในที่นี้กำหนดให้เป็น 0.16 เท่าของค่าสูงสุด (แต่ค่าที่เหมาะจริงๆควรจะเป็นเท่าไหร่อาจไม่มีคำตอบตายตัว ต้องลองผิดลองถูกดู)
watthu = np.where(khwamluek>khwamluek.max()*0.16,1,0)
plt.imshow(watthu,cmap='gray')
plt.tight_layout()
plt.show()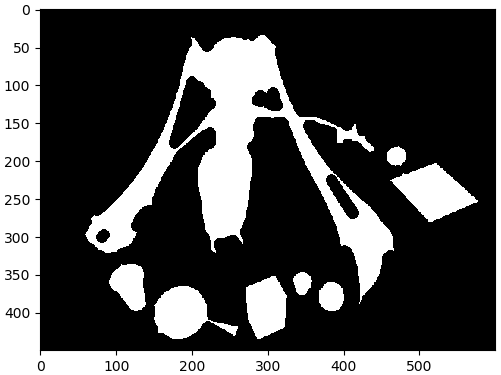
ทีนี้ก็จะได้แต่ละส่วนแยกกันทั้งหมด แต่สูญเสียส่วนขอบไปมาก ส่วนขอบที่เสียไปนี้จะไปเรียกกลับมาอีกทีภายหลังด้วย cv2.watershed()
ต่อมาแยกเอาส่วนที่แน่ชัดแล้วว่าเป็นฉากหลัง คือส่วนที่ได้ความลึกเป็น 0 จากนั้นเอามารวมกับส่วนที่เป็นวัตถุแน่นอน ให้มีค่าไปด้วย จะเหลือบริเวณรอยต่อสีดำตรงกลางแบ่งแยกบริเวณวัตถุกับฉากหลัง
chaklang = np.where(khwamluek==0,1,0)
nae = ((watthu+chaklang)!=0).astype(np.uint8)
plt.imshow(nae,cmap='gray')
plt.tight_layout()
plt.show()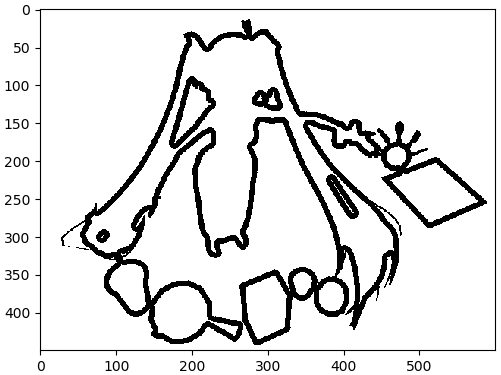
จากนั้นใช้ cv2.connectedComponents() ดูก็จะได้บริเวณของวัตถุและฉากหลังแยกกันทั้งหมด
n,lek = cv2.connectedComponents(nae)
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()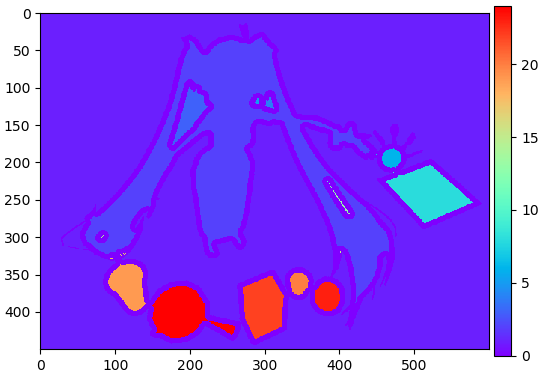
เพียงแต่ส่วนฉากหลังเองก็ถูกแยกย่อยออกมาหมดเช่นกัน ให้ทำการเปลี่ยนกลับเป็นค่าเลขเดียวกันโดยถมด้วยเลข 1 ไป
ส่วนบริเวณที่เป็นรอยต่อให้ทำเป็น -1
แต่ก่อนอื่นเอาทั้งหมดมา +2 ก่อนเพื่อให้แน่ใจว่าทุกตัวมีค่า 2 ขึ้นไป ก่อนที่จะกำหนดให้ส่วนฉากหลังเป็น 1 และรอยต่อเป็น -1
นอกจากนี้ก็จัดเรียงตัวเลขใหม่ให้ไล่ตั้งแต่ 2 ไปโดยไม่เว้นค่าไหนไป เสร็จแล้วก็จะได้แบบนี้
lek += 2
lek[chaklang==1] = 1
lek[nae==0] = -1
for i,n in enumerate(np.unique(lek)[1:],1):
lek[lek==n] = i
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()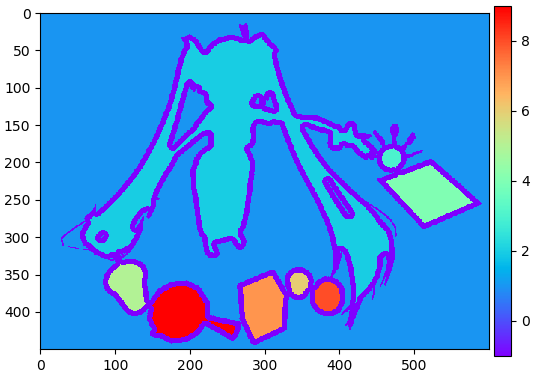
การที่เตรียมรอยต่อให้เป็น -1 และส่วนอื่นให้เห็น 1 ขึ้นไปนั้นเป็นการเตรียมการเพื่อจะใช้ cv2.watershed() นั่นเอง หน้าที่ของฟังก์ชันนี้ก็คือจะช่วยขยายพื้นที่ส่วนที่เป็นหมายเลข 1 ขึ้นไปให้ไปคลุมทับบริเวณรอยแบ่งซึ่งมีค่าเป็น -1
คราวนี้ได้เวลาใช้ cv2.watershed() แล้ว ค่าที่ต้องใส่ก็คือตัวรูปภาพเดิมที่เป็นภาพสีก่อนแปลง กับข้อมูลหมายเลขที่เตรียมไว้นี้ ตัวภาพเดิมจะเป็นตัวตัดสินว่าบริเวณหมายเลขใดจะไปท่วมส่วนไหน
lek = cv2.watershed(miku,lek)
plt.imshow(lek,cmap='rainbow')
plt.colorbar(pad=0.01)
plt.tight_layout()
plt.show()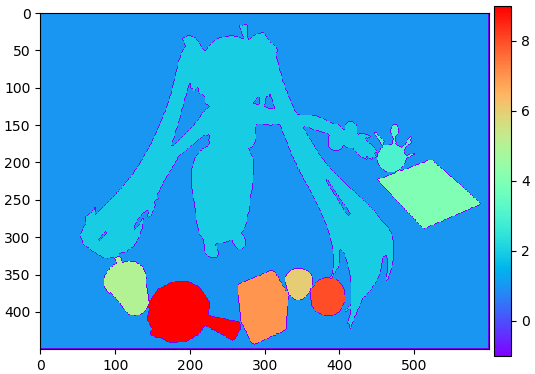
ผลที่ได้จะเป็นภาพที่บริเวณส่วนต่างๆถูกขยายไปจนทับส่วนรอยแบ่งจนเต็มเกือบหมด เหลือเพียงเส้นกั้นบางๆ จะเห็นว่าคราวนี้แต่ละสีครอบคลุมพื้นที่วัตถุแต่ละอันแยกกันหมด
สุดท้ายลองวาดเส้นเค้าโครงของแต่ละตัวทีละตัวแยกกัน
contour = []
for i in range(2,lek.max()+1):
c,_ = cv2.findContours((lek==i).astype(np.uint8),cv2.RETR_EXTERNAL,cv2.CHAIN_APPROX_SIMPLE)
contour.append(c[0])
n_contour = len(contour)
si = plt.get_cmap('rainbow')(np.arange(n_contour)/(n_contour-1))[:,[2,1,0]]*255
for i in range(n_contour):
miku = cv2.drawContours(miku,contour,i,si[i],2)
cv2.imwrite('miku16c09.jpg',miku)
เท่านี้ก็สามารถแบ่งวัตถุที่มีส่วนติดกันอยู่ออกจากกันได้สำเร็จ อาจมีส่วนที่ดูไม่สมบูรณ์อยู่บ้าง สามารถลองปรับค่าต่างๆแล้วลองใหม่หรือเพิ่มขั้นตอนอื่นๆเช่นการแปลงสัณฐาน อาจได้ผลที่ดีขึ้นได้
อ่านบทถัดไป >> บทที่ ๑๗
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> opencv-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib