โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๔: อนุพันธ์และกฎลูกโซ่ของอาเรย์
เขียนเมื่อ 2018/08/26 23:23
แก้ไขล่าสุด 2022/07/10 21:11
>> ต่อจาก บทที่ ๓
ในบทที่แล้วได้แนะนำวิธีการใช้ฟังก์ชันกระตุ้นฟังก์ชันกระตุ้นและการเคลื่อนลงตามความชันไป
เพื่อความง่ายในการเข้าใจจึงได้เขียนแยกพิจารณาข้อมูลทีละตัวแล้วค่อยนำมารวมกัน
แต่ในทางปฏิบัติแล้วที่จริงจะนิยมคำนวณในรูปแบบของอาเรย์มากกว่า ยิ่งหากไปต่อเรื่อยๆการคำนวณจะยิ่งซับซ้อน การอธิบายตัวแปรต่างๆในรูปของอาเรย์จะเหมาะสมกว่า
อีกทั้งในไพธอนการคำนวณแบบอาเรย์จะเร็วกว่าการวนซ้ำด้วย for มากเพื่อคำนวณทีละตัวมาก
เพียงแต่ว่ามีความยากในการทำความเข้าใจอยู่ บทนี้จะมาไล่ทำความเข้าใจไปช้าๆทีละขั้น
เริ่มแรก ในบทที่แล้วเราพิจารณาอนุพันธ์ของค่าเสียหายเทียบกับน้ำหนักทีละตัว คือ ∂J/∂wj แบบนี้
แต่คราวนี้จะพิจารณาในรูปของอาเรย์ คือ
..(4.1)
โดย m คือจำนวนตัวแปรต้น
ย้ำอีกรอบว่าสัญลักษณ์ลูกษรบนหัวใช้แสดงว่าเป็นอาเรย์หนึ่งมิติในแนวตั้ง (ก็คือเวกเตอร์) ถ้าหากใช้อักษรตัวหนาจะเป็นอาเรย์สองมิติ ส่วนตัวเอียงคือค่าเลขตัวเดียว
จะเห็นว่าอนุพันธ์ของปริมาณเลขตัวเดียว (สเกลาร์) เทียบกับอาเรย์ ผลที่ได้ก็จะเป็นการหาอนุพันธ์เทียบกับทุกตัวในอาเรย์ จะได้อาเรย์ขนาดเท่ากับอาเรย์นั้น
แล้วกฎลูกโซ่ก็ใช้ได้เหมือนกัน
..(4.2)
ในที่นี้ h เองก็เป็นอาเรย์
..(4.3)
ค่า J คำนวณจาก h แต่ละค่าได้โดย
..(4.4)
ดังนั้นได้ว่า
..(4.5)
a เองก็เป็นอาเรย์เช่นเดียวกับ h
..(4.6)
และเนื่องจาก a และ h เป็นปริมาณที่มีจำนวนตัวแปรเท่ากัน จึงนำทั้งอาเรย์มาคำนวณกันได้โดยตรง
..(4.7)
และจาก (4.5) และ (4.7) จะได้ว่า
..(4.8)
ต่อมาพิจารณาอนุพันธ์ของ a เทียบกับ w
a คำนวณจาก w และ b โดย
..(4.9)
อนึ่ง ในที่นี้เครื่องหมายด็อตจะหมายถึงการเอาอาเรย์มาคูณกันแบบเมทริกซ์ ในไพธอนใช้คำสั่ง np.dot() ในขณะที่ถ้าเอาตัวแปรมาต่อกันเฉยๆจะเป็นการเอาสมาชิกทั้งหมดมาคูณกันธรรมดา
ตรงนี้จะยากกว่าหน่อย เพราะ a กับ w เป็นอาเรย์หนึ่งมิติเหมือนกันก็จริง แต่ว่าความหมายของมิติต่างกัน a เป็นมิติของข้อมูลและตัว มีขนาดเป็น n ส่วน w เป็นมิติของแต่ละตัวแปรต้น มีขนาดเป็น m
ดังนั้นการหาอนุพันธ์ของ a เทียบกับ w จึงต้องเป็นการแจกแจงเกิดเป็นอาเรย์สองมิติแบบนี้
..(4.10)
ในที่นี้ a กระจายในแนวตั้ง w กระจายในแนวนอน ส่วนถ้าถามว่าอันไหนจะกลายเป็นแนวตั้งหรือแนวนอนนั้น ที่จริงอาจไม่ได้มีหลักตายตัวแต่แค่พิจารณาความสะดวกในการคำนวณเป็นหลัก
แล้วก็จะพบว่ามันมีค่าเท่ากับอาเรย์ x พอดี
..(4.11)
ส่วนอนุพันธ์เทียบ b นั้น เนื่องจาก b เป็นเลขตัวเดียวในขณะที่ a เป็นอาเรย์ จึงเป็นการหาอนุพันธ์ของ a แต่ละตัวเทียบกับ b ซึ่งจะเห็นว่าทุกตัวได้ 1 หมด ดังนั้นจะได้เป็น
..(4.12)
สุดท้ายก็แทนลงในสมการ (4.2) แต่ว่าตรงนี้จะมีปัญหานิดหน่อยก็คือ ขนาดของอาเรย์ไม่เท่ากัน คือ ∂J/∂ai เป็นอาเรย์หนึ่งมิติขนาด n ส่วน ∂ai/∂wj เป็นอาเรย์สองมิติขนาด n×m แต่ผลลัพธ์ที่ได้คือ ∂J/∂wj นั้นจะต้องมีขนาดเป็น m
เมื่อพิจารณาตรงนี้เราจึงรู้ได้ว่าเขียนในรูปคูณกันเฉยๆตามสมการ (4.2) นั้นไม่ถูกต้องนัก จริงๆแล้วควรจะอยู่ในรูปของการคูณเมทริกซ์ แบบนี้
..(4.13)
ที่รู้ว่าเป็นแบบนี้เพราะความสัมพันธ์ของขนาดเมทริกซ์เวลาคูณกันเป็น [m×n][n×1] = [m×1]
ก็คือขนาดมิติหลังของตัวแรกกับมิติแรกของตัวหลังจะต้องเท่ากัน และผลที่ได้จะเป็นอาเรย์ขนาดเท่ากับมิติแรกของตัวแรกและมิติหลังของตัวหลัง
ต่อมา ในทำนองเดียวกันก็สามารถพิจารณาหาอนุพันธ์ของค่าเสียหายเทียบกับ b ได้เป็น
..(4.14)
สุดท้ายก็นำค่าอนุพันธ์มาใช้ปรับค่า
..(4.15)
เขียนโปรแกรม
สร้างข้อมูลกลุ่มแบบนี้ขึ้นมาใช้เป็นตัวอย่าง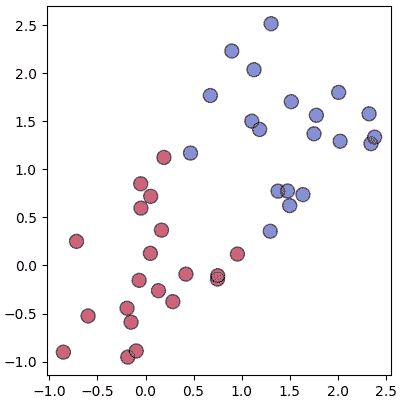
เราอาจเขียนโปรแกรมให้เรียนรู้ในลักษณะเดียวกับบทที่แล้วแต่เปลี่ยนมาใช้การคำนวณทั้งอาเรย์ได้เป็นแบบนี้
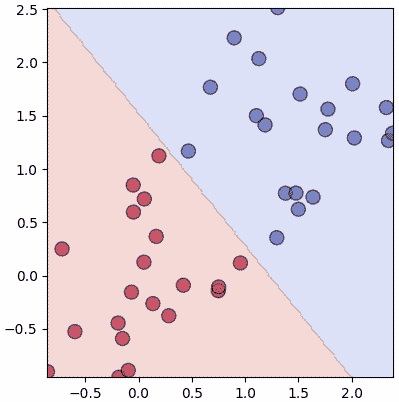
ดูแล้วเรียบง่ายกว่าเดิม ไม่ต้องมีวังวน for ซ้อนด้านในแล้ว แค่ใช้ dot กับ sum ในการคำนวณกับอาเรย์ได้เลย
ค่าเอนโทรปีและความสัดส่วนจะนวนที่ทายถูกในแต่ละรอบก็ได้ถูกบันทึกไว้ ลองนำมาวาดกราฟดูความเปลี่ยนแปลงได้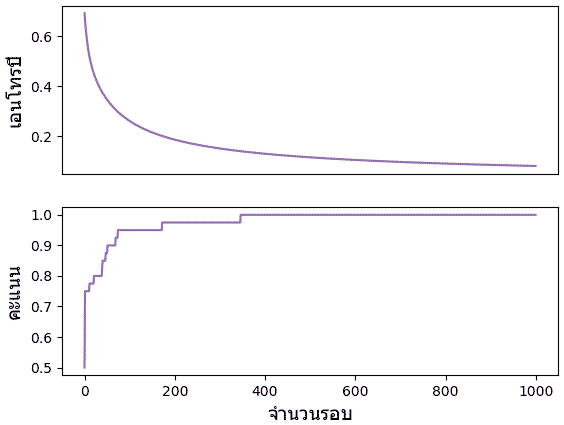
ลองแสดงเป็นภาพเคลื่อนไหวได้ดังนี้
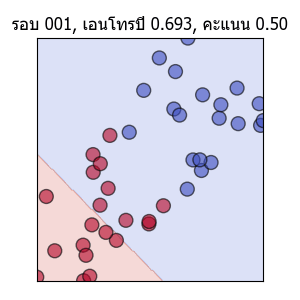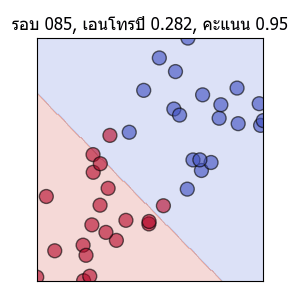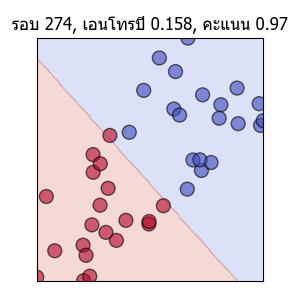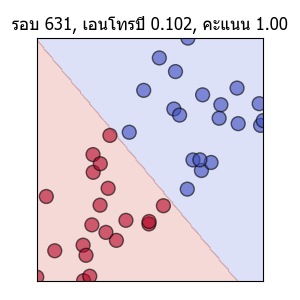
พอเส้นแบ่งพาดผ่านตรงกลาง คะแนนก็จะเป็น 1.0 แต่ความเปลี่ยนแปลงก็ยังมีต่อไปโดยเอนโทรปีจะยังคงลดลงได้อีก และเส้นก็ถูกปรับให้แบ่งอยู่ใกล้ตรงกลางมากขึ้นเรื่อยๆด้วย
เขียนเป็นคลาส
เพื่อความเป็นระเบียบต่อจากนี้ไปจะเขียนแบบจำลองการเรียนรู้ในรูปแบบของคลาส
วิธีการใช้ก็คือ
- สร้างออบเจ็กต์ของคลาส
- ป้อนข้อมูลให้เรียนรู้โดยใช้เมธอด .rianru()
- เมื่อเรียนรู้เสร็จก็นำมาใช้ทำนายผลได้ด้วยเมธอด .thamnai()
ขอทดสอบการใช้โดยใช้วิเคราะห์ข้อมูลที่สร้างขึ้นเองโดยใช้โค้ดในนี้ >> https://phyblas.hinaboshi.com/20180811
ข้อมูลสามารถโหลดได้จาก >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar
ข้อมูลนี้เป็นรูปร่างต่างๆ ๕ ชนิด จำนวนรูปละ 1000 รวมทั้งหมดเป็น 5000 ขนาด 25×25
ถ้าใครต้องการสร้างข้อมูลขึ้นเองก็ทำได้โดยใช้ฟังก์ชันจากในนั้น
อาจลองปรับขนาดหรือจำนวนแล้วลองใหม่ด้วยตัวเองดูได้ ใช้ข้อมูลต่างกันอาจเห็นผลอะไรต่างๆกันไป
ข้อมูลนี้มีรูปอยู่ ๕ ชนิด แต่เพอร์เซปตรอนที่เราสร้างในบทนี้มีไว้ใช้แค่แบ่งข้อมูล ๒ ชนิด ดังนั้นเราจะใช้แค่ ๒ ชนิดแรก รวมแล้ว 2000 รูป
ชนิดแรกคือวงกลม อยู่ในโฟลเดอร์ 0 ส่วนชนิดต่อมาคือสามเหลี่ยม อยู่ในโฟลเดอร์ 1 เราสามารถใช้ glob เพื่อทำการดึงชื่อไฟล์มาแล้วไล่เปิดด้วย plt.imread()
ตัวอย่างรูป
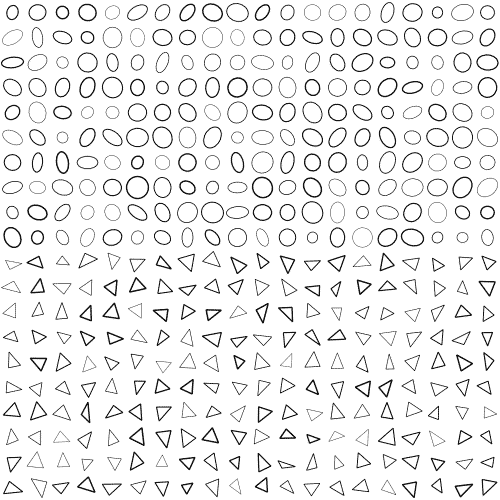
รูปมีขนาด 25×25 ดังนั้นประกอบขึ้นจาก 625 จุด ทั้ง 625 จุดนี้คือตัวแปรต้นที่จะนำมาใช้วิเคราะห์
แต่ภาพที่อ่านขึ้นมาเสร็จจะอยู่ในรูปของอาเรย์ขนาด (จำนวนรูป,25,25) ต้องปรับให้เป็น (จำนวนรูป,625) เพราะเราจะป้อนทุกจุดในฐานะข้อมูลตัวแปรนึง ไม่ได้สนตำแหน่งของจุด
นอกจากนี้ เราจะใช้แค่ชนิดละ 900 รูปในการเรียนรู้ และเก็บอีก 100 เอาไว้ใช้ทดสอบ
จะเห็นว่าแค่วิธีการง่ายๆเพอร์เซปตรอนชั้นเดียวแค่นี้ก็สามารถวิเคราะห์รูปภาพและจำแนกได้แม่นยำกว่า 90% แล้ว และการที่สามารถทายได้แม่นแม้แต่ข้อมูลที่ไม่ได้ใช้ในการฝึกด้วยก็แสดงให้เห็นว่าใช้ได้ดีจริง
โดยสรุปแล้ว การเข้าใจหลักการคำนวณของอาเรย์และเมทริกซ์นั้นอาจมีความซับซ้อนแต่ก็ค่อนข้างจำเป็นสำหรับการเข้าใจการคำนวณภายในโครงข่ายประสาทเทียม
>> อ่านต่อ บทที่ ๕
ในบทที่แล้วได้แนะนำวิธีการใช้ฟังก์ชันกระตุ้นฟังก์ชันกระตุ้นและการเคลื่อนลงตามความชันไป
เพื่อความง่ายในการเข้าใจจึงได้เขียนแยกพิจารณาข้อมูลทีละตัวแล้วค่อยนำมารวมกัน
แต่ในทางปฏิบัติแล้วที่จริงจะนิยมคำนวณในรูปแบบของอาเรย์มากกว่า ยิ่งหากไปต่อเรื่อยๆการคำนวณจะยิ่งซับซ้อน การอธิบายตัวแปรต่างๆในรูปของอาเรย์จะเหมาะสมกว่า
อีกทั้งในไพธอนการคำนวณแบบอาเรย์จะเร็วกว่าการวนซ้ำด้วย for มากเพื่อคำนวณทีละตัวมาก
เพียงแต่ว่ามีความยากในการทำความเข้าใจอยู่ บทนี้จะมาไล่ทำความเข้าใจไปช้าๆทีละขั้น
เริ่มแรก ในบทที่แล้วเราพิจารณาอนุพันธ์ของค่าเสียหายเทียบกับน้ำหนักทีละตัว คือ ∂J/∂wj แบบนี้
แต่คราวนี้จะพิจารณาในรูปของอาเรย์ คือ
..(4.1)
โดย m คือจำนวนตัวแปรต้น
ย้ำอีกรอบว่าสัญลักษณ์ลูกษรบนหัวใช้แสดงว่าเป็นอาเรย์หนึ่งมิติในแนวตั้ง (ก็คือเวกเตอร์) ถ้าหากใช้อักษรตัวหนาจะเป็นอาเรย์สองมิติ ส่วนตัวเอียงคือค่าเลขตัวเดียว
จะเห็นว่าอนุพันธ์ของปริมาณเลขตัวเดียว (สเกลาร์) เทียบกับอาเรย์ ผลที่ได้ก็จะเป็นการหาอนุพันธ์เทียบกับทุกตัวในอาเรย์ จะได้อาเรย์ขนาดเท่ากับอาเรย์นั้น
แล้วกฎลูกโซ่ก็ใช้ได้เหมือนกัน
..(4.2)
ในที่นี้ h เองก็เป็นอาเรย์
..(4.3)
ค่า J คำนวณจาก h แต่ละค่าได้โดย
..(4.4)
ดังนั้นได้ว่า
..(4.5)
a เองก็เป็นอาเรย์เช่นเดียวกับ h
..(4.6)
และเนื่องจาก a และ h เป็นปริมาณที่มีจำนวนตัวแปรเท่ากัน จึงนำทั้งอาเรย์มาคำนวณกันได้โดยตรง
..(4.7)
และจาก (4.5) และ (4.7) จะได้ว่า
..(4.8)
ต่อมาพิจารณาอนุพันธ์ของ a เทียบกับ w
a คำนวณจาก w และ b โดย
..(4.9)
อนึ่ง ในที่นี้เครื่องหมายด็อตจะหมายถึงการเอาอาเรย์มาคูณกันแบบเมทริกซ์ ในไพธอนใช้คำสั่ง np.dot() ในขณะที่ถ้าเอาตัวแปรมาต่อกันเฉยๆจะเป็นการเอาสมาชิกทั้งหมดมาคูณกันธรรมดา
ตรงนี้จะยากกว่าหน่อย เพราะ a กับ w เป็นอาเรย์หนึ่งมิติเหมือนกันก็จริง แต่ว่าความหมายของมิติต่างกัน a เป็นมิติของข้อมูลและตัว มีขนาดเป็น n ส่วน w เป็นมิติของแต่ละตัวแปรต้น มีขนาดเป็น m
ดังนั้นการหาอนุพันธ์ของ a เทียบกับ w จึงต้องเป็นการแจกแจงเกิดเป็นอาเรย์สองมิติแบบนี้
..(4.10)
ในที่นี้ a กระจายในแนวตั้ง w กระจายในแนวนอน ส่วนถ้าถามว่าอันไหนจะกลายเป็นแนวตั้งหรือแนวนอนนั้น ที่จริงอาจไม่ได้มีหลักตายตัวแต่แค่พิจารณาความสะดวกในการคำนวณเป็นหลัก
แล้วก็จะพบว่ามันมีค่าเท่ากับอาเรย์ x พอดี
..(4.11)
ส่วนอนุพันธ์เทียบ b นั้น เนื่องจาก b เป็นเลขตัวเดียวในขณะที่ a เป็นอาเรย์ จึงเป็นการหาอนุพันธ์ของ a แต่ละตัวเทียบกับ b ซึ่งจะเห็นว่าทุกตัวได้ 1 หมด ดังนั้นจะได้เป็น
..(4.12)
สุดท้ายก็แทนลงในสมการ (4.2) แต่ว่าตรงนี้จะมีปัญหานิดหน่อยก็คือ ขนาดของอาเรย์ไม่เท่ากัน คือ ∂J/∂ai เป็นอาเรย์หนึ่งมิติขนาด n ส่วน ∂ai/∂wj เป็นอาเรย์สองมิติขนาด n×m แต่ผลลัพธ์ที่ได้คือ ∂J/∂wj นั้นจะต้องมีขนาดเป็น m
เมื่อพิจารณาตรงนี้เราจึงรู้ได้ว่าเขียนในรูปคูณกันเฉยๆตามสมการ (4.2) นั้นไม่ถูกต้องนัก จริงๆแล้วควรจะอยู่ในรูปของการคูณเมทริกซ์ แบบนี้
..(4.13)
ที่รู้ว่าเป็นแบบนี้เพราะความสัมพันธ์ของขนาดเมทริกซ์เวลาคูณกันเป็น [m×n][n×1] = [m×1]
ก็คือขนาดมิติหลังของตัวแรกกับมิติแรกของตัวหลังจะต้องเท่ากัน และผลที่ได้จะเป็นอาเรย์ขนาดเท่ากับมิติแรกของตัวแรกและมิติหลังของตัวหลัง
ต่อมา ในทำนองเดียวกันก็สามารถพิจารณาหาอนุพันธ์ของค่าเสียหายเทียบกับ b ได้เป็น
..(4.14)
สุดท้ายก็นำค่าอนุพันธ์มาใช้ปรับค่า
..(4.15)
เขียนโปรแกรม
สร้างข้อมูลกลุ่มแบบนี้ขึ้นมาใช้เป็นตัวอย่าง
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(7)
X = np.random.normal(0,0.5,[40,2])
X[:20] += 1.5
z = np.zeros(40)
z[20:] += 1
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='k',alpha=0.6,cmap='coolwarm')
plt.show()
เราอาจเขียนโปรแกรมให้เรียนรู้ในลักษณะเดียวกับบทที่แล้วแต่เปลี่ยนมาใช้การคำนวณทั้งอาเรย์ได้เป็นแบบนี้
def sigmoid(x):
return 1/(1+np.exp(-x))
def ha_entropy(z,h):
return -(z*np.log(h)+(1-z)*np.log(1-h)).mean()
w = np.array([0,0.])
b = 0
eta = 0.1
entropy = []
khanaen = []
for o in range(1000):
a = np.dot(X,w) + b
h = sigmoid(a)
ga = (h-z)/len(z)
gw = np.dot(X.T,ga)
gb = ga.sum()
w -= eta*gw
b -= eta*gb
entropy.append(ha_entropy(z,h)) # เอนโทรปี
khanaen.append(((a>=0)==z).mean()) # คะแนน (สัดส่วนที่ทายถูก)
lins = np.linspace(-0.5,1.5,200)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
mh = np.dot(mX,w) + b
mz = (mh>=0).astype(int).reshape(200,-1)
plt.axes(aspect=1,xlim=(X[:,0].min(),X[:,0].max()),ylim=(X[:,1].min(),X[:,1].max()))
plt.contourf(mx,my,mz,cmap='coolwarm',alpha=0.2)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='k',alpha=0.6,cmap='coolwarm')
plt.show()
ดูแล้วเรียบง่ายกว่าเดิม ไม่ต้องมีวังวน for ซ้อนด้านในแล้ว แค่ใช้ dot กับ sum ในการคำนวณกับอาเรย์ได้เลย
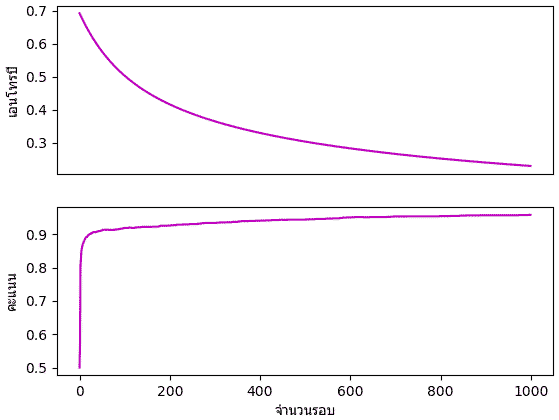
ค่าเอนโทรปีและความสัดส่วนจะนวนที่ทายถูกในแต่ละรอบก็ได้ถูกบันทึกไว้ ลองนำมาวาดกราฟดูความเปลี่ยนแปลงได้
plt.subplot(211,xticks=[])
plt.plot(entropy,'C4')
plt.ylabel(u'เอนโทรปี',family='Tahoma',size=14)
plt.subplot(212)
plt.plot(khanaen,'C4')
plt.ylabel(u'คะแนน',family='Tahoma',size=14)
plt.xlabel(u'จำนวนรอบ',family='Tahoma',size=14)
plt.show()
ลองแสดงเป็นภาพเคลื่อนไหวได้ดังนี้

พอเส้นแบ่งพาดผ่านตรงกลาง คะแนนก็จะเป็น 1.0 แต่ความเปลี่ยนแปลงก็ยังมีต่อไปโดยเอนโทรปีจะยังคงลดลงได้อีก และเส้นก็ถูกปรับให้แบ่งอยู่ใกล้ตรงกลางมากขึ้นเรื่อยๆด้วย
เขียนเป็นคลาส
เพื่อความเป็นระเบียบต่อจากนี้ไปจะเขียนแบบจำลองการเรียนรู้ในรูปแบบของคลาส
class ThotthoiLogistic:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.w = np.zeros(X.shape[1])
self.b = 0
self.entropy = []
self.khanaen = []
for i in range(n_thamsam):
a = self.ha_a(X)
h = sigmoid(a)
J = ha_entropy(z,h)
ga = (h-z)/len(z)
self.w -= self.eta*np.dot(ga,X)
self.b -= self.eta*ga.sum()
self.entropy.append(J)
khanaen = ((a>=0)==z).mean()
self.khanaen.append(khanaen)
def thamnai(self,X):
return (self.ha_a(X)>=0).astype(int)
def ha_a(self,X):
return np.dot(X,self.w) + self.bวิธีการใช้ก็คือ
- สร้างออบเจ็กต์ของคลาส
- ป้อนข้อมูลให้เรียนรู้โดยใช้เมธอด .rianru()
- เมื่อเรียนรู้เสร็จก็นำมาใช้ทำนายผลได้ด้วยเมธอด .thamnai()
ขอทดสอบการใช้โดยใช้วิเคราะห์ข้อมูลที่สร้างขึ้นเองโดยใช้โค้ดในนี้ >> https://phyblas.hinaboshi.com/20180811
ข้อมูลสามารถโหลดได้จาก >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar
ข้อมูลนี้เป็นรูปร่างต่างๆ ๕ ชนิด จำนวนรูปละ 1000 รวมทั้งหมดเป็น 5000 ขนาด 25×25
ถ้าใครต้องการสร้างข้อมูลขึ้นเองก็ทำได้โดยใช้ฟังก์ชันจากในนั้น
sangrup(n=5000,d=25,misi=0)อาจลองปรับขนาดหรือจำนวนแล้วลองใหม่ด้วยตัวเองดูได้ ใช้ข้อมูลต่างกันอาจเห็นผลอะไรต่างๆกันไป
ข้อมูลนี้มีรูปอยู่ ๕ ชนิด แต่เพอร์เซปตรอนที่เราสร้างในบทนี้มีไว้ใช้แค่แบ่งข้อมูล ๒ ชนิด ดังนั้นเราจะใช้แค่ ๒ ชนิดแรก รวมแล้ว 2000 รูป
ชนิดแรกคือวงกลม อยู่ในโฟลเดอร์ 0 ส่วนชนิดต่อมาคือสามเหลี่ยม อยู่ในโฟลเดอร์ 1 เราสามารถใช้ glob เพื่อทำการดึงชื่อไฟล์มาแล้วไล่เปิดด้วย plt.imread()
ตัวอย่างรูป
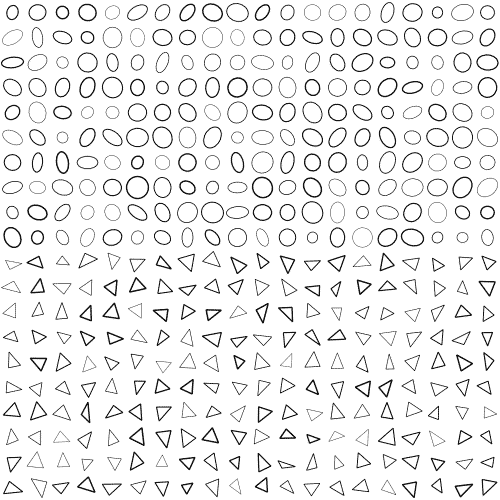
รูปมีขนาด 25×25 ดังนั้นประกอบขึ้นจาก 625 จุด ทั้ง 625 จุดนี้คือตัวแปรต้นที่จะนำมาใช้วิเคราะห์
แต่ภาพที่อ่านขึ้นมาเสร็จจะอยู่ในรูปของอาเรย์ขนาด (จำนวนรูป,25,25) ต้องปรับให้เป็น (จำนวนรูป,625) เพราะเราจะป้อนทุกจุดในฐานะข้อมูลตัวแปรนึง ไม่ได้สนตำแหน่งของจุด
นอกจากนี้ เราจะใช้แค่ชนิดละ 900 รูปในการเรียนรู้ และเก็บอีก 100 เอาไว้ใช้ทดสอบ
from glob import glob
d = 25
X1 = np.array([plt.imread(x) for x in glob('ruprang-raisi-25x25x1000x5/0/*.png')]).reshape(-1,625)
X2 = np.array([plt.imread(x) for x in glob('ruprang-raisi-25x25x1000x5/1/*.png')]).reshape(-1,625)
X = np.vstack([X1[:900],X2[:900]]) # คัดเฉพาะ 900 รูปแรกของแต่ละแบบ นำมารวมกัน
z = np.arange(2).repeat(900) # คำตอบ เลข 0 และ 1
tl = ThotthoiLogistic(eta=0.01) # สร้างออบเจ็กต์ของคลาสการถดถอยโลจิสติก
tl.rianru(X,z,n_thamsam=1000) # ทำการเรียนรู้
plt.subplot(211,xticks=[])
plt.plot(tl.entropy,'m')
plt.ylabel(u'เอนโทรปี',family='Tahoma')
plt.subplot(212)
plt.plot(tl.khanaen,'m')
plt.ylabel(u'คะแนน',family='Tahoma')
plt.xlabel(u'จำนวนรอบ',family='Tahoma')
plt.show()
# นำข้อมูล 100 ตัวที่เหลือมาลองทำนายผล แล้วเทียบกับคำตอบจริง
Xo = np.vstack([X1[900:],X2[900:]])
zo = np.arange(2).repeat(100)
print((tl.thamnai(Xo)==zo).mean()) # ได้ 0.92
จะเห็นว่าแค่วิธีการง่ายๆเพอร์เซปตรอนชั้นเดียวแค่นี้ก็สามารถวิเคราะห์รูปภาพและจำแนกได้แม่นยำกว่า 90% แล้ว และการที่สามารถทายได้แม่นแม้แต่ข้อมูลที่ไม่ได้ใช้ในการฝึกด้วยก็แสดงให้เห็นว่าใช้ได้ดีจริง
โดยสรุปแล้ว การเข้าใจหลักการคำนวณของอาเรย์และเมทริกซ์นั้นอาจมีความซับซ้อนแต่ก็ค่อนข้างจำเป็นสำหรับการเข้าใจการคำนวณภายในโครงข่ายประสาทเทียม
>> อ่านต่อ บทที่ ๕
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy