การจัดการกับจำนวนเชิงซ้อนใน python
เขียนเมื่อ 2016/06/08 23:34
แก้ไขล่าสุด 2022/07/16 19:42
ในเนื้อหาภาษาไพธอนเบื้องต้นบทที่ ๓ ซึ่งกล่าวถึงเรื่องตัวแปรและชนิดของข้อมูลไปนั้นได้แนะนำไปว่าภาษาไพธอนมี ชนิดข้อมูลชนิดจำนวนเชิงซ้อนอยู่ด้วย นั่นคือ complex
เพียงแต่ว่าตลอดเนื้อหาหลักนั้นแทบจะไม่มีการพูดถึงจำนวนเชิงซ้อนเลย นั่นเป็นเพราะว่าในการใช้งานโดยส่วนใหญ่นั้นมักจะไม่จำเป็นต้องใช้
อย่างไรก็ตามสำหรับงานวิจัยทางวิทยาศาสตร์แล้วบ่อยครั้งที่เราอาจต้องยุ่งกับ จำนวนเชิงซ้อน แม้ว่าจะเป็นสิ่งที่เข้าใจยากแต่ก็ไม่อาจเลี่ยงได้ ดังนั้นก็จำเป็นต้องมาเรียนรู้ไว้สักหน่อย
จำนวนเชิงซ้อนคือจำนวนที่ประกอบไปด้วยส่วนจริงและส่วนจินตภาพ
ในภาษาไพธอนส่วนจินตภาพถูกเขียนแทนด้วยตัว j ตามหลังตัวเลข
การสร้างจำนวนเชิงซ้อน
การสร้างข้อมูลชนิดจำนวนเชิงซ้อนขึ้นมาทำได้โดยพิมพ์ตัวเลขในรูปแบบส่วนจริงบวกส่วนจินตภาพ เช่น
ให้ระวังไว้ด้วยว่าแม้ส่วนจินตภาพจะมีค่า 1 ก็ไม่อาจละเลข 1 หน้าตัว j ได้ เพราะถ้าไม่มีเลขนำหน้าตัว j จะถูกตีความเป็นตัวแปรธรรมดาตัวหนึ่ง
ในไพธอน 3 จำนวนเชิงซ้อนยังสามารถสร้างขึ้นจากการนำจำนวนจริงติดลบมายกกำลังด้วย
แต่ถ้าทำแบบนี้ในไพธอน 2 จะขึ้นว่า ValueError: negative number cannot be raised to a fractional power
อีกวิธีในการสร้างคือใช้ฟังก์ชัน complex โดยใส่อาร์กิวเมนต์ตัวแรกเป็นส่วนจริง ตัวหลังเป็นส่วนจินตภาพ หรือถ้าใส่แค่ตัวเดียวก็จะได้ส่วนจินตภาพเป็น 0
แอตทริบิวต์และเมธอดภายในจำนวนเชิงซ้อน
จำนวนเชิงซ้อนประกอบด้วยส่วนจริงและส่วนจินตภาพ ซึ่งสามารถดูค่าได้โดยดูที่แอตทริบิวต์ real กับ imag
สำหรับการสังยุค (การกลับค่าความเป็นบวกลบของส่วนจินตภาพ) ทำได้โดยใช้เมธอด conjugate
การแสดงจำนวนเชิงซ้อนในรูปพิกัดเชิงขั้ว
จำนวนเชิงซ้อนนอกจากจะแสดงในรูป x+yi แล้วยังสามารถแสดงได้ในรูปของพิกัดเชิงขั้วดังนี้

โดยที่ r คือค่าสัมบูรณ์และ θ คือมุมเฟส
การจะแปลงเป็นพิกัดเชิงชั้วต้องใช้ฟังก์ชันจากมอดูล cmath ซึ่งเป็นมอดูลสำหรับจัดการกับจำนวนเชิงซ้อนโดยเฉพาะ
เราสามารถแปลงจำนวนเชิงซ้อนให้เขียนอยู่ในรูปของ r และ θ ได้โดยใช้ฟังก์ชัน polar ใน cmath
จะได้ทูเพิลที่มีสมาชิกตัวแรกเป็น r และตัวหลังเป็น θ โดยหน่วยมุมในที่นี้เป็นเรเดียน
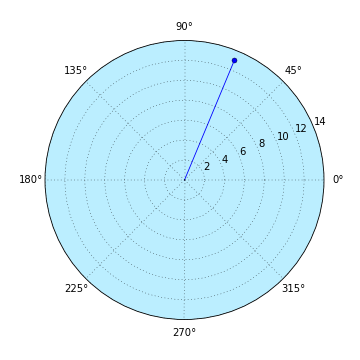
ภาพแสดงจำนวนเชิงซ้อนในระบบพิกัดเชิงขั้ว (วาดโดย matplotlib)
นอกจากนั้นเราอาจหาค่า r ด้วยฟังก์ชัน abs ซึ่งเป็นฟังก์ชันมาตรฐานก็ได้
ส่วน θ หาได้ด้วยฟังก์ชัน phase ใน cmath
และในทางกลับกันสามารถแปลงค่าที่เป็นพิกัดเชิงขั้วกลับเป็นรูป x+yi ได้ด้วยฟังก์ชัน rect ใน cmath
ฟังก์ชันอื่นๆใน cmath
มอดูล cmath นั้นประกอบไปด้วยฟังก์ชันที่เหมือนกันกับในมอดูล math มากมาย เช่น exp, log, sqrt, sin, asin, sinh เป็นต้น
ฟังก์ชันเหล่านี้สามารถทำงานได้เหมือนกับใน math เพียงแต่ว่าจะให้ผลลัพธ์เป็นข้อมูลชนิดจำนวนเชิงซ้อนเสมอ แม้ว่าจะไม่มีส่วนจินตภาพเกิดขึ้นเลยก็ตาม
ฟังก์ชันใน math นั้นโดยทั่วไปไม่สามารถใช้กับจำนวนเชิงซ้อนได้ หรือแม้แต่ฟังก์ชันที่ใช้จำนวนจริงแต่ควรให้ผลเป็นจำนวนเชิงซ้อนก็จะเกิดข้อ ผิดพลาด
เช่นฟังก์ชัน sqrt นั้นถ้าเป็นของ math จะไม่สามารถถอดรากจำนวนลบได้ ในขณะที่ใน cmath จะถอดรากแล้วได้จำนวนเชิงซ้อน
อ้างอิง
เพียงแต่ว่าตลอดเนื้อหาหลักนั้นแทบจะไม่มีการพูดถึงจำนวนเชิงซ้อนเลย นั่นเป็นเพราะว่าในการใช้งานโดยส่วนใหญ่นั้นมักจะไม่จำเป็นต้องใช้
อย่างไรก็ตามสำหรับงานวิจัยทางวิทยาศาสตร์แล้วบ่อยครั้งที่เราอาจต้องยุ่งกับ จำนวนเชิงซ้อน แม้ว่าจะเป็นสิ่งที่เข้าใจยากแต่ก็ไม่อาจเลี่ยงได้ ดังนั้นก็จำเป็นต้องมาเรียนรู้ไว้สักหน่อย
จำนวนเชิงซ้อนคือจำนวนที่ประกอบไปด้วยส่วนจริงและส่วนจินตภาพ
ในภาษาไพธอนส่วนจินตภาพถูกเขียนแทนด้วยตัว j ตามหลังตัวเลข
การสร้างจำนวนเชิงซ้อน
การสร้างข้อมูลชนิดจำนวนเชิงซ้อนขึ้นมาทำได้โดยพิมพ์ตัวเลขในรูปแบบส่วนจริงบวกส่วนจินตภาพ เช่น
z = 1+3j
print(z) # ได้ (1+3j)
print(type(z)) # ได้ <type 'complex'>
print(z) # ได้ (1+3j)
print(type(z)) # ได้ <type 'complex'>
ให้ระวังไว้ด้วยว่าแม้ส่วนจินตภาพจะมีค่า 1 ก็ไม่อาจละเลข 1 หน้าตัว j ได้ เพราะถ้าไม่มีเลขนำหน้าตัว j จะถูกตีความเป็นตัวแปรธรรมดาตัวหนึ่ง
ในไพธอน 3 จำนวนเชิงซ้อนยังสามารถสร้างขึ้นจากการนำจำนวนจริงติดลบมายกกำลังด้วย
print((-20)**0.5) # ได้ (2.7383934913210134e-16+4.47213595499958j)
แต่ถ้าทำแบบนี้ในไพธอน 2 จะขึ้นว่า ValueError: negative number cannot be raised to a fractional power
อีกวิธีในการสร้างคือใช้ฟังก์ชัน complex โดยใส่อาร์กิวเมนต์ตัวแรกเป็นส่วนจริง ตัวหลังเป็นส่วนจินตภาพ หรือถ้าใส่แค่ตัวเดียวก็จะได้ส่วนจินตภาพเป็น 0
print(complex(4,6.1)) # ได้ (4+6.1j)
print(complex(4)) # ได้ (4+0j)
print(complex(0,6.1)) # ได้ 6.1j
print(complex(4)) # ได้ (4+0j)
print(complex(0,6.1)) # ได้ 6.1j
แอตทริบิวต์และเมธอดภายในจำนวนเชิงซ้อน
จำนวนเชิงซ้อนประกอบด้วยส่วนจริงและส่วนจินตภาพ ซึ่งสามารถดูค่าได้โดยดูที่แอตทริบิวต์ real กับ imag
print((1+13j).real) # ได้ 1
print((1+13j).imag) # ได้ 13
print((1+13j).imag) # ได้ 13
สำหรับการสังยุค (การกลับค่าความเป็นบวกลบของส่วนจินตภาพ) ทำได้โดยใช้เมธอด conjugate
print((1+13j).conjugate()) # ได้ (1-13j)
การแสดงจำนวนเชิงซ้อนในรูปพิกัดเชิงขั้ว
จำนวนเชิงซ้อนนอกจากจะแสดงในรูป x+yi แล้วยังสามารถแสดงได้ในรูปของพิกัดเชิงขั้วดังนี้

โดยที่ r คือค่าสัมบูรณ์และ θ คือมุมเฟส
การจะแปลงเป็นพิกัดเชิงชั้วต้องใช้ฟังก์ชันจากมอดูล cmath ซึ่งเป็นมอดูลสำหรับจัดการกับจำนวนเชิงซ้อนโดยเฉพาะ
เราสามารถแปลงจำนวนเชิงซ้อนให้เขียนอยู่ในรูปของ r และ θ ได้โดยใช้ฟังก์ชัน polar ใน cmath
import cmath
print(cmath.polar(5+12j)) # ได้ (13.0, 1.176005207095135)
print(cmath.polar(5+12j)) # ได้ (13.0, 1.176005207095135)
จะได้ทูเพิลที่มีสมาชิกตัวแรกเป็น r และตัวหลังเป็น θ โดยหน่วยมุมในที่นี้เป็นเรเดียน
ภาพแสดงจำนวนเชิงซ้อนในระบบพิกัดเชิงขั้ว (วาดโดย matplotlib)

นอกจากนั้นเราอาจหาค่า r ด้วยฟังก์ชัน abs ซึ่งเป็นฟังก์ชันมาตรฐานก็ได้
print(abs(5+12j)) # ได้ 13.0
ส่วน θ หาได้ด้วยฟังก์ชัน phase ใน cmath
print(cmath.phase(5+12j)) # ได้ 1.1760052071
และในทางกลับกันสามารถแปลงค่าที่เป็นพิกัดเชิงขั้วกลับเป็นรูป x+yi ได้ด้วยฟังก์ชัน rect ใน cmath
print(cmath.rect(13,1.176005271)) # ได้ (4.99999923314+12.0000003195j)
ฟังก์ชันอื่นๆใน cmath
มอดูล cmath นั้นประกอบไปด้วยฟังก์ชันที่เหมือนกันกับในมอดูล math มากมาย เช่น exp, log, sqrt, sin, asin, sinh เป็นต้น
ฟังก์ชันเหล่านี้สามารถทำงานได้เหมือนกับใน math เพียงแต่ว่าจะให้ผลลัพธ์เป็นข้อมูลชนิดจำนวนเชิงซ้อนเสมอ แม้ว่าจะไม่มีส่วนจินตภาพเกิดขึ้นเลยก็ตาม
print(math.sin(1.3)) # ได้ 0.9974949866040544
print(cmath.sin(1.3)) # ได้ (0.9974949866040544+0j)
print(cmath.sin(1.3)) # ได้ (0.9974949866040544+0j)
ฟังก์ชันใน math นั้นโดยทั่วไปไม่สามารถใช้กับจำนวนเชิงซ้อนได้ หรือแม้แต่ฟังก์ชันที่ใช้จำนวนจริงแต่ควรให้ผลเป็นจำนวนเชิงซ้อนก็จะเกิดข้อ ผิดพลาด
เช่นฟังก์ชัน sqrt นั้นถ้าเป็นของ math จะไม่สามารถถอดรากจำนวนลบได้ ในขณะที่ใน cmath จะถอดรากแล้วได้จำนวนเชิงซ้อน
print(math.sqrt(-3)) # ได้ ValueError: math domain error
print(cmath.sqrt(-3)) # ได้ 1.7320508075688772j
print(cmath.sqrt(-3)) # ได้ 1.7320508075688772j
อ้างอิง