maya python เบื้องต้น บทที่ ๘: สร้างรูปทรงต่างๆให้หลากหลาย
เขียนเมื่อ 2016/03/10 17:31
แก้ไขล่าสุด 2021/09/28 16:42
ในบทแรกสุดได้แนะนำรูปทรงซึ่งง่ายสุดไปสองอย่างแล้ว นั่นคือทรงสี่เหลี่ยมและทรงกลม สำหรับในตอนนี้จะมาลองสร้างวัตถุอื่นๆหลากหลายขึ้นไปอีก นอกจากนี้จะแนะนำองค์ประกอบอื่นๆอีกมากขึ้น
รูปทรงอื่นๆทีจะแนะนำนั้นได้แก่
polyCylinder() ทรงกระบอก
polyCone() ทรงกรวย
polyPrism() ทรงปริซึม
polyPyramid() ทรงพีรามิด
polyPlane() พื้นระนาบสี่เหลี่ยม
จะเห็นว่าทั้งหมดนี้มีคำว่า poly นำหน้า คำสั่งเหล่านี้ทั้งหมดสำหรับสร้างวัตถุเป็นโพลิกอน แต่ว่าที่จริงแล้วนอกเหนือจากนี้ก็ยังมีคำสั่งที่ใช้ในการสร้างวัตถุชนิด "พื้นผิว NURBS" ซึ่งก็จะกล่าวถึงในตอนถัดๆไป อย่างไรก็ตามโดยทั่วไปแล้วโพลิกอนถูกใช้บ่อยกว่าพื้นผิวมากเนื่องจากความ สะดวกในการใช้งาน ดังนั้นจึงจะกล่าวถึงโพลิกอนเป็นหลัก
และจะสังเกตว่าหลังคำว่า poly นั้นตัวแรกต้องเป็นตัวพิมพ์ใหญ่เสมอ ถ้าพิมพ์ตัวเล็กจะไม่ทำงาน ต้องระวังด้วย ส่วนคำว่า poly นั้นจะพิมพ์ p เป็นตัวพิมพ์เล็กหรือใหญ่ก็ได้
polyCylinder() กับ polyCone() เป็นฟังก์ชันคำสั่งสร้างทรงกระบอกและทรงกรวย ตามลำดับ มีแฟล็กเหมือนกันหมด ได้แก่
ตัวอย่าง
ลองดูแล้วเทียบรูปทรงต่างๆที่ปรากฏขึ้นมา ซึ่งแต่ละอันมีขนาดเท่ากันแต่จำนวนส่วนที่แบ่งตามแนวต่างๆไม่เท่ากัน

สำหรับ sx นั้นถ้าหากมีค่าน้อยเกินไปวัตถุจะดูเหมือนไม่ค่อยกลม กลายเป็นเหมือนกับปริซึมหรือพีรามิดไป
polyPrism() เป็นฟังก์ชันคำสั่งสร้างทรงปริซึม แฟล็กเกี่ยวกับรูปร่างมีดังนี้
ตัวอย่าง ลองวนซ้ำสร้างปริซึมที่มีจำนวนด้านไม่เท่ากันขึ้นมาเปรียบเทียบกัน

polyPyramid() เป็นฟังก์ชันคำสั่งสร้างทรงพีรามิด แฟล็กเกี่ยวกับรูปร่างได้แก่
แฟล็กของพีรามิดจะคล้ายๆกับปริซึม ต่างกันตรงที่ไม่มี l ซึ่งคือความสูง นั่นเพราะความสูงจะเท่ากับความกว้างของด้าน
ส่วน polyPlane() เป็นฟังก์ชันคำสั่งสร้างระนาบสี่เหลี่ยม แฟล็กเกี่ยวกับรูปร่างได้แก่
ระนาบที่ได้จะมีอยู่ด้านเดียว หันขึ้นด้านบน
นอกจากนี้ก็ยังมีรูปทรงอื่นๆอีกเช่น
polyPipe() สร้างท่อ
polyTorus() สร้างทรงโดนัท
polyHelix() สร้างทรงเกลียว
เป็นต้น
ตอนนี้เราสามารถสร้างวัตถุขึ้นมาได้หลายชนิดแล้ว โดยที่สามารถปรับรูปร่างได้หลากหลาย
อย่างไรก็ตามก็ยังมีอีกอย่างหนึ่งซึ่งควรจะสามารถปรับได้แต่ยังไม่ได้พูดถึง นั่นคือตำแหน่งที่วัตถุหัน
ถ้าสังเกตมาจนถึงตอนนี้จะเห็นว่าวัตถุทั้งหมดที่สร้างขึ้นจะตั้งตรงโดยที่มีแกน y เป็นแกนหมุน สำหรับกรวยและพีรามิดจะหันปลายแหลมไปด้านบนตลอด
แต่ความจริงแล้วเราสามารถเปลี่ยนทิศที่รูปทรงนั้นหันไปได้ ด้วยการเติมแฟล็กเพิ่มเข้าไปอีกตัว นั่นคือ ax (axis) ซึ่งใช้ได้กับฟังก์ชันสร้างรูปทรงทั้งหมดที่กล่าวมาแล้ว
ax นั้นรับค่าเว็กเตอร์ชี้ทิศที่ต้องการให้เป็นแกนเป็นตัวแปรชนิดลิสต์ของจำนวนจริง ๓ ตัว เช่น
จะได้ทรงกระบอกที่หันไปในทิศเดียวกับเวกเตอร์ (1,1,1)
ลองใช้กับทรงกรวย หมุนดูให้เห็นหลายๆทิศเทียบกัน
ลองเปรียบเทียบทิศทางที่หันของทรงกรวยแต่ละอันดูจะพอเห็นภาพขึ้นมาได้

แฟล็ก ax นี้สนใจแค่ทิศของเว็กเตอร์ โดยไม่สนขนาด ดังนั้นหากสัดส่วนของค่าแต่ละพิกัดเท่ากันแล้วไม่ว่าจะค่ามากหรือน้อยวัตถุ ก็หันไปทิศเดียวกัน ดังนั้น
และ
ต่างได้วัตถุที่หันไปทางเดียวกัน เป็นต้น
โดยปกติแล้วถ้าไม่มีการใส่แฟล็กนี้ค่าตั้งต้นก็คือ [0,1,0] นั่นคือหันไปตามแกน y ด้านบวก ก็คือหันหัวขึ้น
ถ้าหากใส่เป็น ax=[1,0,0] ก็จะหันไปตามแนวแกน x
และถ้าใส่ ax=[0,0,1] ก็จะหันไปตามแนวแกน z เป็นต้น
ขอยกอีกตัวอย่างเพื่อให้เห็นภาพ เป็นการสร้างพีรามิดที่หันไปทั้ง ๖ ด้าน
ค่าต่างๆที่เราใส่ลงไปในแฟล็กตอนที่สร้างรูปทรงเหล่านี้ขึ้น หลังจากที่รูปทรงถูกสร้างขึ้นมาแล้วก็ไม่ได้หายไปไหน สามารถเปิดดูได้จากในแชนเนลบ็อกซ์ (チャネルボックス, channel box) และ แอตทริบิวต์อีดิเตอร์ (アトリビュートエディタ, attribute editor) ซึ่งอยู่ในแถบทางฝั่งขวาทั้งสองอัน

ลองสร้างวัตถุสักอย่างแล้วก็กดเปิดแอตทริบิวต์อีดิเตอร์
เช่น ลองกดสร้างทรงปริซึมห้าด้าน
จะเห็นว่ามีแถบให้เลือกอยู่หลายอัน แต่ละอันแทนสิ่งที่เรียกว่า "โหนด" อันแรกจะเห็นเป็นชื่อของวัตถุที่เราตั้งนั้นคือโหนดหลักของตัววัตถุ ซึ่งแสดงถึงคุณสมบัติภาพรวมของตัววัตถุ
ส่วนอันอื่นๆถัดไปเป็นโหนดที่เก็บคุณสมบัติอื่นๆ เช่น รูปร่าง สี ฯลฯ ซึ่งอาจมีเพิ่มขึ้นมาเรื่อยๆเมื่อใช้คำสั่งทำอะไรกับรูปทรงนี้ต่อไป แต่ในตอนเริ่มแรกวัตถุที่เพิ่งถูกสร้างขึ้นมาจากรูปทรงเริ่มต้นควรจะมี ๕ โหนด
เมื่อกดดูที่อันแรกคือโหนดหลักของวัตถุจะเห็นค่าที่แสดงตำแหน่ง มุมที่หมุน และมาตราส่วน
ตำแหน่งเริ่มต้นจะอยู่ที่ (0,0,0) แต่ถ้ามีการเคลื่อนย้ายวัตถุ เช่นด้วยการใช้ฟังก์ชัน move() ก็จะมีค่าเปลี่ยนแปลงไป หรือสามารถกดคลิกทีตัวเลขแล้วพิมพ์แก้ค่าได้เลย ส่วนค่าอื่นๆเช่นมุมที่หมุน และมาตรส่วนก็สามารถปรับค่าได้เช่นกัน แต่ตอนนี้จะยังไม่พูดถึง
ส่วนอันที่สองจะเห็นเป็นชื่อของวัตถุตามด้วย Shape ตรงส่วนนี้เป็นโหนดหนึ่งของวัตถุซึ่งถูกสร้างขึ้นมาพร้อมกัน ทำหน้าที่กำหนดรูปร่างของวัตถุตอนที่เรนเดอร์ ซึ่งตรงส่วนนี้จะขอยังไม่พูดถึงละเอียด
และส่วนอันที่ ๓ จะเป็นส่วนแสดงโหนดที่เก็บข้อมูลของรูปทรงที่ก่อตัวเป็นวัตถุนี้ ชื่อที่เห็นนี้ถูกตั้งโดยอัตโนมัติโดยไม่เกี่ยวกับชื่อวัตถุที่ตั้ง และไม่สามารถกำหนดตอนสร้างวัตถุได้ แต่ถ้าอยากเปลี่ยนก็สามารถทำได้ด้วยฟังก์ชัน rename()
สำหรับกรณีนี้ชื่อที่ได้คือ polyPrism1
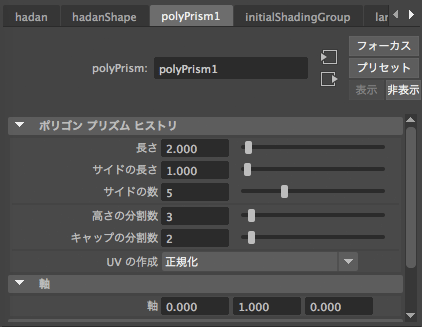
พอลองคลิกเข้ามาดูก็จะเห็นค่าองค์ประกอบต่างๆแสดงอยู่ตามภาพ นี่เป็นกรณีของทรงปริซึม
สามารถคลิกเข้าไปแก้ค่าแต่ละอันได้ แล้วรูปร่างของวัตถุก็จะเปลี่ยนไปตามค่าที่ใส่ เหมือนกับการใส่ค่าลงไปในแฟล็กตั้งแต่ตอนที่สร้าง
นอกจากนี้ก็ยังสามารถดูและแก้ค่าได้ผ่านทาง channel box ด้วย เพียงแต่จะมีรายละเอียดน้อยกว่า
หากต้องการทราบค่าเหล่านี้ด้วยการใช้ฟังก์ชันในไพธอนโดยที่ไม่ต้องมาเปิดดู attribute editor ก็สามารถทำได้ด้วยฟังก์ชัน getAttr() และหากต้องการเปลี่ยนค่าเหล่านี้ก็สามารถทำได้ด้วยการใช้ฟังก์ชัน setAttr()
ทั้งสองฟังก์ชันนี้จะอธิบายในบทถัดๆไป ตอนนี้จะยังไม่พูดถึง
โดยปกติเวลาที่ใช้ฟังก์ชันสร้างรูปทรงในการสร้างวัตถุขึ้นมาจะมีสิ่งที่เรียก ว่า "ประวัติศาสตร์" ซึ่งบอกให้รู้ว่าวัตถุนั้นมีจุดกำเนิดเริ่มสร้างมายังไง โดยจะเก็บไว้ในโหนดตามที่เห็นได้ใน attribute editor นี้ และทำให้สามารถกลับไปแก้ด้วยการเปลี่ยนค่าองค์ประกอบต่างๆของรูปทรงนั้นๆ
แต่หากมั่นใจว่าจะไม่มีการกลับมาแก้ตรงนี้อีกแล้วก็สามารถลบโหนดนี้ออกได้ โดยการเพิ่มแฟล็กลงไปอีกอย่างในตอนที่สร้าง แฟล็กนั้นคือ ch (constructionHistory)
ลองลบปริซึมอันเดิมแล้วพิมพ์
ผลที่ได้จะได้รูปทรงเหมือนเดิมทุกอย่าง แต่หากดูใน attribute editor จะเห็นว่าแถบโหนดของรูปทรงหายไป เหลืออยู่เพียง ๔ แถบเท่านั้น พอเป็นแบบนี้แล้วก็จะไม่สามารถแก้ไขรูปทรงได้
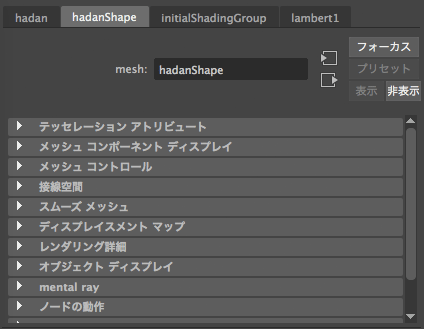
การใส่ ch=0 (ch=False) ลงไปมีความหมายว่าเราไม่ต้องการให้เก็บประวัติศาสตร์การสร้างไว้ วัตถุที่ได้จะไม่จำว่าตัวมันกำเนิดมาจากทรงปริซึม
โดยปกติถ้าไม่ได้ ใส่แฟล็ก ch ลงไปค่าตั้งต้นของแฟล็ก ch คือ 1 (True) หมายความว่าจะมีการเก็บประวัติการสร้างไว้ตลอดหากเราไม่ได้ระบุให้ ch=0
ตอนนี้ได้แนะนำฟังก์ชันสร้างรูปทรงต่างๆไปเยอะแล้ว อีกทั้งแนะนำแฟล็กที่สำคัญไปหลายอย่าง ทำให้สร้างรูปทรงพื้นฐานได้หลากหลายในระดับหนึ่ง ที่เหลือก็คือนำรูปทรงพื้นฐานเหล่านี้ไปแปลงรูปต่อเพื่อให้เป็นรูปร่างที่ ต้องการต่อไป
อ้างอิง
รูปทรงอื่นๆทีจะแนะนำนั้นได้แก่
polyCylinder() ทรงกระบอก
polyCone() ทรงกรวย
polyPrism() ทรงปริซึม
polyPyramid() ทรงพีรามิด
polyPlane() พื้นระนาบสี่เหลี่ยม
จะเห็นว่าทั้งหมดนี้มีคำว่า poly นำหน้า คำสั่งเหล่านี้ทั้งหมดสำหรับสร้างวัตถุเป็นโพลิกอน แต่ว่าที่จริงแล้วนอกเหนือจากนี้ก็ยังมีคำสั่งที่ใช้ในการสร้างวัตถุชนิด "พื้นผิว NURBS" ซึ่งก็จะกล่าวถึงในตอนถัดๆไป อย่างไรก็ตามโดยทั่วไปแล้วโพลิกอนถูกใช้บ่อยกว่าพื้นผิวมากเนื่องจากความ สะดวกในการใช้งาน ดังนั้นจึงจะกล่าวถึงโพลิกอนเป็นหลัก
และจะสังเกตว่าหลังคำว่า poly นั้นตัวแรกต้องเป็นตัวพิมพ์ใหญ่เสมอ ถ้าพิมพ์ตัวเล็กจะไม่ทำงาน ต้องระวังด้วย ส่วนคำว่า poly นั้นจะพิมพ์ p เป็นตัวพิมพ์เล็กหรือใหญ่ก็ได้
polyCylinder() กับ polyCone() เป็นฟังก์ชันคำสั่งสร้างทรงกระบอกและทรงกรวย ตามลำดับ มีแฟล็กเหมือนกันหมด ได้แก่
| h | (height) | ความสูง ค่าเป็นจำนวนจริงที่มากกว่า 0 ค่าตั้งต้นคือ 2 |
| r | (radius) | รัศมี ค่าเป็นจำนวนจริงที่มากกว่า 0 ค่าตั้งต้นคือ 1 |
| sx | (subdivisionsX) | จำนวนส่วนที่แบ่งตามแนวเส้นรอบวง ค่าเป็นจำนวนเต็ม มีค่าตั้งแต่ 3 ขึ้นไป ค่าตั้งต้นคือ 20 |
| sy | (subdivisionsY) | จำนวนส่วนที่แบ่งตามแนวตั้ง ค่าเป็นจำนวนเต็ม มีค่าตั้งแต่ 1 ขึ้นไป ค่าตั้งต้นคือ 1 |
| sz | (subdivisionsZ) | จำนวนส่วนที่แบ่งตามแนวรัศมี ค่าเป็นจำนวนเต็ม มีค่าตั้งแต่ 0 ขึ้นไป ค่าตั้งต้นคือ 1 |
ตัวอย่าง
i=1
while(i<6):
j=1
while(j<6):
k=1
while(k<6):
mc.polyCylinder(sx=i*5,sy=j,sz=k)
mc.move(3*i,3*j,10*k)
mc.polyCone(sx=i*5,sy=j,sz=k)
mc.move(3*i+20,3*j,10*k)
k+=1
j+=1
i+=1
while(i<6):
j=1
while(j<6):
k=1
while(k<6):
mc.polyCylinder(sx=i*5,sy=j,sz=k)
mc.move(3*i,3*j,10*k)
mc.polyCone(sx=i*5,sy=j,sz=k)
mc.move(3*i+20,3*j,10*k)
k+=1
j+=1
i+=1
ลองดูแล้วเทียบรูปทรงต่างๆที่ปรากฏขึ้นมา ซึ่งแต่ละอันมีขนาดเท่ากันแต่จำนวนส่วนที่แบ่งตามแนวต่างๆไม่เท่ากัน

สำหรับ sx นั้นถ้าหากมีค่าน้อยเกินไปวัตถุจะดูเหมือนไม่ค่อยกลม กลายเป็นเหมือนกับปริซึมหรือพีรามิดไป
polyPrism() เป็นฟังก์ชันคำสั่งสร้างทรงปริซึม แฟล็กเกี่ยวกับรูปร่างมีดังนี้
| ns | (numberOfSides) | จำนวนด้าน ค่าเป็นจำนวนเต็ม มีค่าตั้งแต่ 3 ขึ้นไป ค่าตั้งต้นคือ 3 |
| w | (sideLength) | ความกว้างของแต่ละด้าน ค่าเป็นจำนวนจริงบวก ค่าตั้งต้นคือ 0 |
| l | (length) | ความสูง (ความยาว) ของแท่งปริซึม ค่าเป็นจำนวนจริงบวก ค่ำตั้งต้นคือ 2 |
| sh | (subdivisionsHeight) | จำนวนส่วนที่แบ่งตามความสูง ค่าเป็นจำนวนเต็มมีค่าตั้งแต่ 1 ขึ้นไป ค่าต้นคือ 1 |
| sc | (subdivisionsCaps) | จำนวนส่วนที่แบ่งตามแนวรัศมีที่ฐาน ค่าเป็นจำนวนเต็มมีค่าตั้งแต่ 0 ขึ้นไป ค่าตั้งต้นคือ 0 |
ตัวอย่าง ลองวนซ้ำสร้างปริซึมที่มีจำนวนด้านไม่เท่ากันขึ้นมาเปรียบเทียบกัน
i=3
while(i<9):
mc.polyPrism(ns=i,sc=i-3)
mc.move(i*4,0,0)
i+=1
while(i<9):
mc.polyPrism(ns=i,sc=i-3)
mc.move(i*4,0,0)
i+=1

polyPyramid() เป็นฟังก์ชันคำสั่งสร้างทรงพีรามิด แฟล็กเกี่ยวกับรูปร่างได้แก่
| ns | (numberOfSides) | จำนวนด้าน ค่าเป็นจำนวนเต็ม มีค่าตั้งแต่ 3 ขึ้นไป ค่าตั้งต้นคือ 3 |
| w | (sideLength) | ความกว้างของแต่ละด้าน ค่าเป็นจำนวนจริงบวก ค่าตั้งต้นคือ 0 |
| sh | (subdivisionsHeight) | จำนวนส่วนที่แบ่งตามความสูง ค่าเป็นจำนวนเต็มมีค่าตั้งแต่ 1 ขึ้นไป ค่าต้นคือ 1 |
| sc | (subdivisionsCaps) | จำนวนส่วนที่แบ่งตามแนวรัศมีที่ฐาน ค่าเป็นจำนวนเต็มมีค่าตั้งแต่ 0 ขึ้นไป ค่าตั้งต้นคือ 0 |
แฟล็กของพีรามิดจะคล้ายๆกับปริซึม ต่างกันตรงที่ไม่มี l ซึ่งคือความสูง นั่นเพราะความสูงจะเท่ากับความกว้างของด้าน
ส่วน polyPlane() เป็นฟังก์ชันคำสั่งสร้างระนาบสี่เหลี่ยม แฟล็กเกี่ยวกับรูปร่างได้แก่
| w | (width) | ความกว้าง (ขนาดในแกน x) ค่าเป็นจำนวนจริงบวก ค่าตั้งต้นคือ 1 |
| h | (height) | ความยาว (ขนาดในแกน z) ค่าเป็นจำนวนจริงบวก ค่าตั้งต้นคือ 1 |
| sx | (subdivisionsX) | จำนวนส่วนที่แบ่งในแนวแกน x ค่าเป็นจำนวนเต็มตั้งแต่ 1 ขึ้นไป ค่าตั้งต้นคือ 10 |
| sy | (subdivisionsY) | จำนวนส่วนที่แบ่งในแนวแกน y ค่าเป็นจำนวนเต็มตั้งแต่ 1 ขึ้นไป ค่าตั้งต้นคือ 10 |
ระนาบที่ได้จะมีอยู่ด้านเดียว หันขึ้นด้านบน
นอกจากนี้ก็ยังมีรูปทรงอื่นๆอีกเช่น
polyPipe() สร้างท่อ
polyTorus() สร้างทรงโดนัท
polyHelix() สร้างทรงเกลียว
เป็นต้น
ตอนนี้เราสามารถสร้างวัตถุขึ้นมาได้หลายชนิดแล้ว โดยที่สามารถปรับรูปร่างได้หลากหลาย
อย่างไรก็ตามก็ยังมีอีกอย่างหนึ่งซึ่งควรจะสามารถปรับได้แต่ยังไม่ได้พูดถึง นั่นคือตำแหน่งที่วัตถุหัน
ถ้าสังเกตมาจนถึงตอนนี้จะเห็นว่าวัตถุทั้งหมดที่สร้างขึ้นจะตั้งตรงโดยที่มีแกน y เป็นแกนหมุน สำหรับกรวยและพีรามิดจะหันปลายแหลมไปด้านบนตลอด
แต่ความจริงแล้วเราสามารถเปลี่ยนทิศที่รูปทรงนั้นหันไปได้ ด้วยการเติมแฟล็กเพิ่มเข้าไปอีกตัว นั่นคือ ax (axis) ซึ่งใช้ได้กับฟังก์ชันสร้างรูปทรงทั้งหมดที่กล่าวมาแล้ว
ax นั้นรับค่าเว็กเตอร์ชี้ทิศที่ต้องการให้เป็นแกนเป็นตัวแปรชนิดลิสต์ของจำนวนจริง ๓ ตัว เช่น
ax=[1,1,1]
mc.polyCylinder(ax=ax)
mc.polyCylinder(ax=ax)
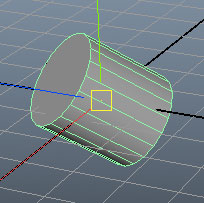
จะได้ทรงกระบอกที่หันไปในทิศเดียวกับเวกเตอร์ (1,1,1)

ลองใช้กับทรงกรวย หมุนดูให้เห็นหลายๆทิศเทียบกัน
i=0
while(i<6):
mc.polyCone(ax=[5-i,i,0])
mc.move(0,0,2*i)
i+=1
while(i<6):
mc.polyCone(ax=[5-i,i,0])
mc.move(0,0,2*i)
i+=1
ลองเปรียบเทียบทิศทางที่หันของทรงกรวยแต่ละอันดูจะพอเห็นภาพขึ้นมาได้

แฟล็ก ax นี้สนใจแค่ทิศของเว็กเตอร์ โดยไม่สนขนาด ดังนั้นหากสัดส่วนของค่าแต่ละพิกัดเท่ากันแล้วไม่ว่าจะค่ามากหรือน้อยวัตถุ ก็หันไปทิศเดียวกัน ดังนั้น
mc.polyCone(ax=[1,1,0])
และ
mc.polyCone(ax=[50,50,0])
ต่างได้วัตถุที่หันไปทางเดียวกัน เป็นต้น
โดยปกติแล้วถ้าไม่มีการใส่แฟล็กนี้ค่าตั้งต้นก็คือ [0,1,0] นั่นคือหันไปตามแกน y ด้านบวก ก็คือหันหัวขึ้น
ถ้าหากใส่เป็น ax=[1,0,0] ก็จะหันไปตามแนวแกน x
และถ้าใส่ ax=[0,0,1] ก็จะหันไปตามแนวแกน z เป็นต้น
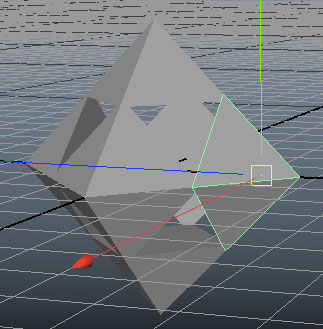
ขอยกอีกตัวอย่างเพื่อให้เห็นภาพ เป็นการสร้างพีรามิดที่หันไปทั้ง ๖ ด้าน
t = [[2,0,0],[0,2,0],[0,0,2],[-2,0,0],[0,-2,0],[0,0,-2]]
i=0
while(i<6):
mc.polyPyramid(ax=t[i],w=2,ns=4)
mc.move(t[i][0],t[i][1],t[i][2])
i+=1
i=0
while(i<6):
mc.polyPyramid(ax=t[i],w=2,ns=4)
mc.move(t[i][0],t[i][1],t[i][2])
i+=1

ค่าต่างๆที่เราใส่ลงไปในแฟล็กตอนที่สร้างรูปทรงเหล่านี้ขึ้น หลังจากที่รูปทรงถูกสร้างขึ้นมาแล้วก็ไม่ได้หายไปไหน สามารถเปิดดูได้จากในแชนเนลบ็อกซ์ (チャネルボックス, channel box) และ แอตทริบิวต์อีดิเตอร์ (アトリビュートエディタ, attribute editor) ซึ่งอยู่ในแถบทางฝั่งขวาทั้งสองอัน

ลองสร้างวัตถุสักอย่างแล้วก็กดเปิดแอตทริบิวต์อีดิเตอร์
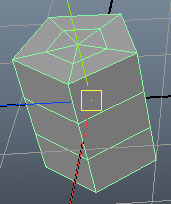
เช่น ลองกดสร้างทรงปริซึมห้าด้าน
mc.polyPrism(ns=5,l=2,w=1,sh=3,sc=2,n='hadan')

จะเห็นว่ามีแถบให้เลือกอยู่หลายอัน แต่ละอันแทนสิ่งที่เรียกว่า "โหนด" อันแรกจะเห็นเป็นชื่อของวัตถุที่เราตั้งนั้นคือโหนดหลักของตัววัตถุ ซึ่งแสดงถึงคุณสมบัติภาพรวมของตัววัตถุ

ส่วนอันอื่นๆถัดไปเป็นโหนดที่เก็บคุณสมบัติอื่นๆ เช่น รูปร่าง สี ฯลฯ ซึ่งอาจมีเพิ่มขึ้นมาเรื่อยๆเมื่อใช้คำสั่งทำอะไรกับรูปทรงนี้ต่อไป แต่ในตอนเริ่มแรกวัตถุที่เพิ่งถูกสร้างขึ้นมาจากรูปทรงเริ่มต้นควรจะมี ๕ โหนด
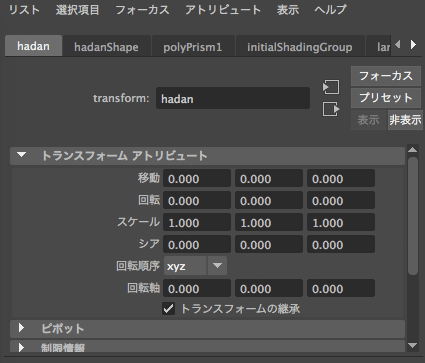
เมื่อกดดูที่อันแรกคือโหนดหลักของวัตถุจะเห็นค่าที่แสดงตำแหน่ง มุมที่หมุน และมาตราส่วน
ตำแหน่งเริ่มต้นจะอยู่ที่ (0,0,0) แต่ถ้ามีการเคลื่อนย้ายวัตถุ เช่นด้วยการใช้ฟังก์ชัน move() ก็จะมีค่าเปลี่ยนแปลงไป หรือสามารถกดคลิกทีตัวเลขแล้วพิมพ์แก้ค่าได้เลย ส่วนค่าอื่นๆเช่นมุมที่หมุน และมาตรส่วนก็สามารถปรับค่าได้เช่นกัน แต่ตอนนี้จะยังไม่พูดถึง
ส่วนอันที่สองจะเห็นเป็นชื่อของวัตถุตามด้วย Shape ตรงส่วนนี้เป็นโหนดหนึ่งของวัตถุซึ่งถูกสร้างขึ้นมาพร้อมกัน ทำหน้าที่กำหนดรูปร่างของวัตถุตอนที่เรนเดอร์ ซึ่งตรงส่วนนี้จะขอยังไม่พูดถึงละเอียด
และส่วนอันที่ ๓ จะเป็นส่วนแสดงโหนดที่เก็บข้อมูลของรูปทรงที่ก่อตัวเป็นวัตถุนี้ ชื่อที่เห็นนี้ถูกตั้งโดยอัตโนมัติโดยไม่เกี่ยวกับชื่อวัตถุที่ตั้ง และไม่สามารถกำหนดตอนสร้างวัตถุได้ แต่ถ้าอยากเปลี่ยนก็สามารถทำได้ด้วยฟังก์ชัน rename()
สำหรับกรณีนี้ชื่อที่ได้คือ polyPrism1

พอลองคลิกเข้ามาดูก็จะเห็นค่าองค์ประกอบต่างๆแสดงอยู่ตามภาพ นี่เป็นกรณีของทรงปริซึม
| 長さ | Length | ความยาว |
| サイドの長さ | Side Length | ความกว้างของแต่ละด้าน |
| サイドの数 | Number of Sides | จำนวนด้าน |
| 高さの分割数 | Height divisions | จำนวนส่วนที่แบ่งตามแนวความสูง |
| キャップの分割数 | Cap divisions | จำนวนส่วนที่แบ่งตามแนวรัศมี |
| 軸 | Axis | แกนหัน ประกอบด้วย ๓ ตัวเลข แทนองค์ประกอบในทิศ x y z |
สามารถคลิกเข้าไปแก้ค่าแต่ละอันได้ แล้วรูปร่างของวัตถุก็จะเปลี่ยนไปตามค่าที่ใส่ เหมือนกับการใส่ค่าลงไปในแฟล็กตั้งแต่ตอนที่สร้าง
นอกจากนี้ก็ยังสามารถดูและแก้ค่าได้ผ่านทาง channel box ด้วย เพียงแต่จะมีรายละเอียดน้อยกว่า
หากต้องการทราบค่าเหล่านี้ด้วยการใช้ฟังก์ชันในไพธอนโดยที่ไม่ต้องมาเปิดดู attribute editor ก็สามารถทำได้ด้วยฟังก์ชัน getAttr() และหากต้องการเปลี่ยนค่าเหล่านี้ก็สามารถทำได้ด้วยการใช้ฟังก์ชัน setAttr()
ทั้งสองฟังก์ชันนี้จะอธิบายในบทถัดๆไป ตอนนี้จะยังไม่พูดถึง
โดยปกติเวลาที่ใช้ฟังก์ชันสร้างรูปทรงในการสร้างวัตถุขึ้นมาจะมีสิ่งที่เรียก ว่า "ประวัติศาสตร์" ซึ่งบอกให้รู้ว่าวัตถุนั้นมีจุดกำเนิดเริ่มสร้างมายังไง โดยจะเก็บไว้ในโหนดตามที่เห็นได้ใน attribute editor นี้ และทำให้สามารถกลับไปแก้ด้วยการเปลี่ยนค่าองค์ประกอบต่างๆของรูปทรงนั้นๆ
แต่หากมั่นใจว่าจะไม่มีการกลับมาแก้ตรงนี้อีกแล้วก็สามารถลบโหนดนี้ออกได้ โดยการเพิ่มแฟล็กลงไปอีกอย่างในตอนที่สร้าง แฟล็กนั้นคือ ch (constructionHistory)
ลองลบปริซึมอันเดิมแล้วพิมพ์
mc.polyPrism(ns=5,l=2,w=1,sh=3,sc=2,n='hadan',ch=0)
ผลที่ได้จะได้รูปทรงเหมือนเดิมทุกอย่าง แต่หากดูใน attribute editor จะเห็นว่าแถบโหนดของรูปทรงหายไป เหลืออยู่เพียง ๔ แถบเท่านั้น พอเป็นแบบนี้แล้วก็จะไม่สามารถแก้ไขรูปทรงได้

การใส่ ch=0 (ch=False) ลงไปมีความหมายว่าเราไม่ต้องการให้เก็บประวัติศาสตร์การสร้างไว้ วัตถุที่ได้จะไม่จำว่าตัวมันกำเนิดมาจากทรงปริซึม
โดยปกติถ้าไม่ได้ ใส่แฟล็ก ch ลงไปค่าตั้งต้นของแฟล็ก ch คือ 1 (True) หมายความว่าจะมีการเก็บประวัติการสร้างไว้ตลอดหากเราไม่ได้ระบุให้ ch=0
ตอนนี้ได้แนะนำฟังก์ชันสร้างรูปทรงต่างๆไปเยอะแล้ว อีกทั้งแนะนำแฟล็กที่สำคัญไปหลายอย่าง ทำให้สร้างรูปทรงพื้นฐานได้หลากหลายในระดับหนึ่ง ที่เหลือก็คือนำรูปทรงพื้นฐานเหล่านี้ไปแปลงรูปต่อเพื่อให้เป็นรูปร่างที่ ต้องการต่อไป
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyCylinder.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyCone.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPrism.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPyramid.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPlane.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyCone.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPrism.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPyramid.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/polyPlane.html