[python] การสร้างเมทริกซ์ความสับสนเพื่อวิเคราะห์ผลการเรียนรู้ของเครื่อง
เขียนเมื่อ 2017/09/26 08:42
แก้ไขล่าสุด 2022/07/21 15:19
บทความนี้ต่อเนื่องจากบทความตอนที่แล้วที่ลองใช้การเรียนรู้ของเครื่องเพื่อจำแนกตัวเลขของข้อมูล MNIST https://phyblas.hinaboshi.com/20170924
โปรแกรมสามารถทายตัวเลขถูกได้มากกว่า 90% ซึ่งเป็นผลที่น่าพอใจ
แต่มีสิ่งที่น่าสนใจซึ่งน่ามาลองมาวิเคราะห์ดูได้ก็คือ เลขไหนทายถูกง่ายหรือยาก และมีการทายเลขไหนผิดไปเป็นเลขไหนมาก
เพื่อให้เห็นภาพชัดลองมาสร้างตารางเพื่อสรุปการทายถูกผิดซึ่งเรียกว่า เมทริกซ์ความสับสน (混淆矩阵, confusion matrix)
ชื่ออาจฟังดูแปลก แต่โดยรวมก็คือเป็นตารางที่สร้างขึ้นมาเพื่อสำหรับไว้ดูเทียบว่ามีการทายสับสนระหว่างตัวไหนกับตัวไหน เป็นวิธีการที่ดีในการวิเคราะห์ผลการทายการจัดหมวดหมู่
ต่อไปจะยกตัวอย่างการเขียนเมทริกซ์ความสับสน อย่างไรก็ตาม โค้ดต่อไปนี้มีตัวแปรที่ต่อเนื่องมาจากตอนที่แล้ว ได้แก่
- X_truat ตัวแปรต้นของชุดข้อมูลตรวจสอบ
- z_truat คำตอบของชุดข้อมูลตรวจสอบ
- tl ออบเจ็กต์ตัวทำถดถอยโลจิสติกที่ฝึกเรียบร้อยแล้ว
หากใครไม่ได้อ่านแล้วทำตามต่อเนื่องมาจากตอนที่แล้วก็ให้เอาโค้ดนี้มารัน จากนั้นค่อยตามขั้นตอนต่อไป
https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_mnist_2.py
การทำเมทริกซ์ค่าสับสนอาจทำได้โดยการเอาผลการทายกับผลเฉลยมาแปลงเป็นแบบวันฮ็อต แล้วก็เอามาคูณเมทริกซ์กัน แบบนี้
ได้
แนวตั้งคือคำตอบจริง แนวนอนคือผลที่ทาย ค่าที่อยู่ในแนวทแยงคือที่ทายถูก ไล่จากบนลงล่าง และซ้ายไปขวา จาก 0 ถึง 9 ตามลำดับ
จากตรงนี้จะเห็นว่ามีการทาย 4 ผิดเป็น 9 เยอะเป็นพิเศษ

รูปนี้คือเลข 4 ที่โปรแกรมทายผิดเป็นเลข 9 สำหรับมนุษย์ทั่วไปอาจดูออกโดยง่าย แต่ตัวโปรแกรมนี้เองอาจเรียนรู้ได้ไม่ถูกต้องสมบูรณ์จึงตัดสินผิดพลาดไปได้
เพื่อให้สร้างเมทริกซ์สับสนได้ง่ายขึ้นอาจใช้ sklearn ช่วยก็ได้
ใน sklearn มีเตรียมฟังก์ชันสำหรับทำตารางนี้ให้โดยอัตโนมัติ ใช้ได้ง่าย แค่ป้อนค่าคำตอบกับค่าที่ทายลงไป
แต่ว่าที่จริงฟังก์ชันที่คล้ายๆกันนี้เราอาจสามารถสร้างขึ้นเองได้ไม่ยากนัก โดยเขียนแค่ ๒ บรรทัด
นอกจากนี้แล้ว ขั้นตอนต่อไปเพื่อให้เห็นภาพชัดยิ่งขึ้นเราอาจลองมาวาดเป็นตารางระบายสีโดยใช้ matplotlib ด้วยได้
ลองเขียนฟังก์ชันแล้วใช้ดู ได้ดังนี้
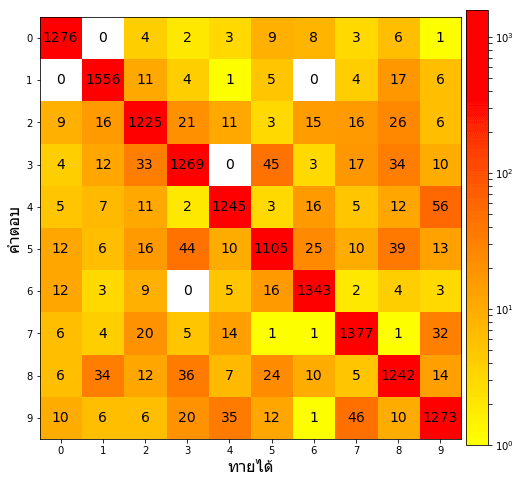
ในภาพนี้สีแดงคือมีจำนวนมาก ส่วนเหลืองคือมีน้อย เนื่องจากที่ทายถูกมีมากดังนั้นแนวทแยงจึงแดง
ในที่นี้เนื่องจากว่าค่าที่ถูกกับผิดต่างกันมากก็เลยใส่ log ลงไปด้วยเพื่อให้สีมีการกระจายตัวเห็นได้ชัดดี
ถ้าไม่ทำให้เป็น log ไปจะกลายเป็นแบบนี้
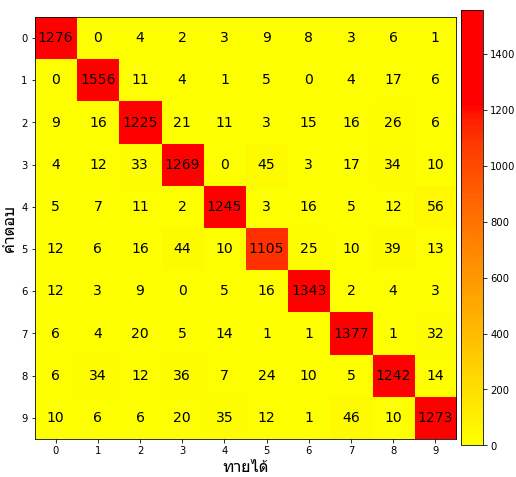
ส่วนที่ทายผิดนั้นแทบจะกลายเป็นสีเดียวกันทั้งหมด แบบนี้ดูยาก ดังนั้นแปลงเป็น log ดีกว่า
กล่าวโดยสรุปก็คือ การนำข้อผิดพลาดมาวิเคราะห์ให้เห็นภาพชัดนั้นก็เป็นทางหนึ่งในการหาทางปรับปรุงอะไรต่างๆ
ดังนั้นการใช้เมทริกซ์ความสับสนเพื่อวิเคราะห์ผลการเรียนรู้ของเครื่องก็เป็นวิธีหนึ่งที่ช่วยในการปรับปรุงโปรแกรมต่อไปได้
อ้างอิง
โปรแกรมสามารถทายตัวเลขถูกได้มากกว่า 90% ซึ่งเป็นผลที่น่าพอใจ
แต่มีสิ่งที่น่าสนใจซึ่งน่ามาลองมาวิเคราะห์ดูได้ก็คือ เลขไหนทายถูกง่ายหรือยาก และมีการทายเลขไหนผิดไปเป็นเลขไหนมาก
เพื่อให้เห็นภาพชัดลองมาสร้างตารางเพื่อสรุปการทายถูกผิดซึ่งเรียกว่า เมทริกซ์ความสับสน (混淆矩阵, confusion matrix)
ชื่ออาจฟังดูแปลก แต่โดยรวมก็คือเป็นตารางที่สร้างขึ้นมาเพื่อสำหรับไว้ดูเทียบว่ามีการทายสับสนระหว่างตัวไหนกับตัวไหน เป็นวิธีการที่ดีในการวิเคราะห์ผลการทายการจัดหมวดหมู่
ต่อไปจะยกตัวอย่างการเขียนเมทริกซ์ความสับสน อย่างไรก็ตาม โค้ดต่อไปนี้มีตัวแปรที่ต่อเนื่องมาจากตอนที่แล้ว ได้แก่
- X_truat ตัวแปรต้นของชุดข้อมูลตรวจสอบ
- z_truat คำตอบของชุดข้อมูลตรวจสอบ
- tl ออบเจ็กต์ตัวทำถดถอยโลจิสติกที่ฝึกเรียบร้อยแล้ว
หากใครไม่ได้อ่านแล้วทำตามต่อเนื่องมาจากตอนที่แล้วก็ให้เอาโค้ดนี้มารัน จากนั้นค่อยตามขั้นตอนต่อไป
https://github.com/phyblas/rianrupython/blob/master/kanrianrukhongkhrueang/thotthoi_mnist_2.py
การทำเมทริกซ์ค่าสับสนอาจทำได้โดยการเอาผลการทายกับผลเฉลยมาแปลงเป็นแบบวันฮ็อต แล้วก็เอามาคูณเมทริกซ์กัน แบบนี้
z_thamnai = tl.thamnai(X_truat)
z_thamnai_1h = (z_thamnai[:,None]==np.arange(10)).astype(int)
z_truat_1h = (z_truat[:,None]==np.arange(10)).astype(int)
conma = np.dot(z_truat_1h.T,z_thamnai_1h)
[print(c) for c in conma]ได้
[1276 0 4 2 3 9 8 3 6 1]
[ 0 1556 11 4 1 5 0 4 17 6]
[ 9 16 1225 21 11 3 15 16 26 6]
[ 4 12 33 1269 0 45 3 17 34 10]
[ 5 7 11 2 1245 3 16 5 12 56]
[ 12 6 16 44 10 1105 25 10 39 13]
[ 12 3 9 0 5 16 1343 2 4 3]
[ 6 4 20 5 14 1 1 1377 1 32]
[ 6 34 12 36 7 24 10 5 1242 14]
[ 10 6 6 20 35 12 1 46 10 1273]แนวตั้งคือคำตอบจริง แนวนอนคือผลที่ทาย ค่าที่อยู่ในแนวทแยงคือที่ทายถูก ไล่จากบนลงล่าง และซ้ายไปขวา จาก 0 ถึง 9 ตามลำดับ
จากตรงนี้จะเห็นว่ามีการทาย 4 ผิดเป็น 9 เยอะเป็นพิเศษ

รูปนี้คือเลข 4 ที่โปรแกรมทายผิดเป็นเลข 9 สำหรับมนุษย์ทั่วไปอาจดูออกโดยง่าย แต่ตัวโปรแกรมนี้เองอาจเรียนรู้ได้ไม่ถูกต้องสมบูรณ์จึงตัดสินผิดพลาดไปได้
เพื่อให้สร้างเมทริกซ์สับสนได้ง่ายขึ้นอาจใช้ sklearn ช่วยก็ได้
ใน sklearn มีเตรียมฟังก์ชันสำหรับทำตารางนี้ให้โดยอัตโนมัติ ใช้ได้ง่าย แค่ป้อนค่าคำตอบกับค่าที่ทายลงไป
from sklearn.metrics import confusion_matrix
conma = confusion_matrix(z_truat,z_thamnai)
[print(c) for c in conma]แต่ว่าที่จริงฟังก์ชันที่คล้ายๆกันนี้เราอาจสามารถสร้างขึ้นเองได้ไม่ยากนัก โดยเขียนแค่ ๒ บรรทัด
def confusion_matrix(z1,z2):
n = max(z1.max(),z2.max())+1
return np.dot((z1==np.arange(n)[:,None]).astype(int),(z2[:,None]==np.arange(n)).astype(int))นอกจากนี้แล้ว ขั้นตอนต่อไปเพื่อให้เห็นภาพชัดยิ่งขึ้นเราอาจลองมาวาดเป็นตารางระบายสีโดยใช้ matplotlib ด้วยได้
ลองเขียนฟังก์ชันแล้วใช้ดู ได้ดังนี้
def plotconma(conma,log=0):
n = len(conma)
plt.figure(figsize=[9,8])
plt.axes(xticks=np.arange(n),xticklabels=np.arange(n),yticks=np.arange(n),yticklabels=np.arange(n))
plt.xlabel(u'ทายได้',fontname='Tahoma',size=16)
plt.ylabel(u'คำตอบ',fontname='Tahoma',size=16)
for i in range(n):
for j in range(n):
plt.text(j,i,conma[i,j],ha='center',va='center',size=14)
if(log):
plt.imshow(conma,cmap='autumn_r',norm=mpl.colors.LogNorm())
else:
plt.imshow(conma,cmap='autumn_r')
plt.colorbar(pad=0.01)
plt.show()
plotconma(conma,log=1)
ในภาพนี้สีแดงคือมีจำนวนมาก ส่วนเหลืองคือมีน้อย เนื่องจากที่ทายถูกมีมากดังนั้นแนวทแยงจึงแดง
ในที่นี้เนื่องจากว่าค่าที่ถูกกับผิดต่างกันมากก็เลยใส่ log ลงไปด้วยเพื่อให้สีมีการกระจายตัวเห็นได้ชัดดี
ถ้าไม่ทำให้เป็น log ไปจะกลายเป็นแบบนี้
plotconma(conma,log=0)
ส่วนที่ทายผิดนั้นแทบจะกลายเป็นสีเดียวกันทั้งหมด แบบนี้ดูยาก ดังนั้นแปลงเป็น log ดีกว่า
กล่าวโดยสรุปก็คือ การนำข้อผิดพลาดมาวิเคราะห์ให้เห็นภาพชัดนั้นก็เป็นทางหนึ่งในการหาทางปรับปรุงอะไรต่างๆ
ดังนั้นการใช้เมทริกซ์ความสับสนเพื่อวิเคราะห์ผลการเรียนรู้ของเครื่องก็เป็นวิธีหนึ่งที่ช่วยในการปรับปรุงโปรแกรมต่อไปได้
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn