[python] ใช้ชุดข้อมูลไวน์เป็นตัวอย่างเพื่อเรียนรู้เรื่องการคัดเลือกค่าแทนลักษณะ
เขียนเมื่อ 2017/12/07 22:05
แก้ไขล่าสุด 2024/10/12 09:25
sklearn ได้มีการเตรียมข้อมูลชนิดต่างๆเอาไว้ให้มากมายสำหรับใช้ทดสอบหรือฝึกฝนการเรียนรู้ของเครื่อง
นอกจากชุดข้อมูลภาพตัวเลขของ MNIST ที่เคยแนะนำไปแล้ว https://phyblas.hinaboshi.com/20170920
ก็ยังมีข้อมูลจำนวนหนึ่งที่มีขนาดเล็กๆและถูกเก็บอยู่ภายในตัวมอดูลอยู่แล้วจึงดึงข้อมูลมาใช้ได้ทันที
ในที่นี้จะลองใช้ข้อมูลหนึ่งในนั้นซึ่งนิยมใช้กันมาก คือชุดข้อมูลไวน์ (wine dataset)

ชุดข้อมูลไวน์ประกอบไปด้วยข้อมูลค่าที่บอกค่าคุณสมบัติต่างๆของไวน์ พร้อมกับบอกว่าเป็นไวน์ชนิดไหน โดยมีการแบ่งเป็น ๓ ชนิด จำนวนข้อมูลมีทั้งหมด ๑๗๘ แถว
ค่าคุณสมบัติต่างๆนั้นมีจำนวนมาก รวมแล้วมีถึง ๑๓ ชนิด นั่นคือเป็นปัญหาที่มีมิติสูงถึง ๑๓ มิติ
เพื่อให้เห็นภาพ ลองดึงข้อมูลมาดูเป็นตัวอย่างแล้วดูว่าข้างในเป็นยังไงบ้าง ข้อมูลอยู่ในแอตทริบิวต์ .data ส่วนเลขชนิดของไวน์อยู่ใน .target
ค่าต่างๆทั้ง ๑๓ นั้นคือค่าของอะไรบ้างสามารถเห็นได้จากในแอตทริบิวต์ .feature_names
ได้
ทั้งหมดนี้คือคุณสมบัติที่จะเอามาใช้แบ่งชนิดของไวน์

เนื่องจากมีจำนวนมิติมาก จึงเหมาะที่จะถูกนำมาใช้เป็นตัวอย่างฝึกเรื่องการคัดเลือกค่าแทนลักษณะ (特征选择, feature selection) คือการเลือกว่าค่าคุณสมบัติอันไหนที่เป็นปัจจัยสำคัญในการทำให้คำตอบเปลี่ยนแปลงไปมากที่สุด
เพราะในจำนวนคุณสมบัติทั้ง ๑๓ อย่างนี้ ไม่ใช่ว่าแต่ละค่าจะสำคัญไปทั้งหมด อาจมีแค่บางค่าที่สำคัญเป็นพิเศษ แต่บางค่าอาจแทบไม่มีผลอะไรต่อคำตอบเลยก็เป็นได้
จริงอยู่ว่าพิจารณาปัจจัยต่างๆเยอะไว้ก่อนไม่เสียหาย แต่บางครั้งก็ทำให้แบบจำลองมีความซับซ้อนเกินไปจนเกิดการเรียนรู้เกินได้ อีกทั้งแน่นอนว่าตัวแปรเยอะก็ใช้เวลาคำนวณนานขึ้น ดังนั้นการพิจารณาลดมิติของปัญหาจึงมีความสำคัญเหมือนกัน
การคัดเลือกว่าคุณสมบัติไหนมีความสำคัญน่านำมาใช้นั้นมีอยู่หลายวิธีมาก ในที่นี้จะลองใช้วิธีการป่าสุ่ม ซึ่งเคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20171117
สำหรับแบบจำลองที่จะใช้ในการแบ่ง คราวนี้ขอเลือกใช้วิธีการเพื่อนบ้านใกล้สุด k ตัวใน sklearn https://phyblas.hinaboshi.com/20171031
และเพื่อให้ผลออกมามั่นใจได้มากขึ้นจะใช้การตรวจสอบแบบไขว้โดยฟังก์ชัน cross_val_score รายละเอียดเขียนไว้ใน https://phyblas.hinaboshi.com/20171020
เริ่มจาก ลองหาค่าความแม่นยำของแบบจำลองโดยใช้ตัวแปรทั้งหมด ๑๓ ตัว
Knn ในที่นี้ใช้ค่าตั้งต้นคือมีจำนวนเพื่อนบ้าน ๕ ตัว และใช้ cv=5 คือแบ่งข้อมูลเป็น ๕ ส่วนในการตรวจสอบแบบไขว้ ทำการคำนวณ ๕ ครั้ง หาความแม่นยำของทั้ง ๕ ครั้งแล้วเอามาเฉลี่ยกันพร้อมหาส่วนเบี่ยงเบนมาตรฐานด้วย
จากนั้นลองมาเร่ิมพิจารณาการลดมิติของปัญหาดูด้วยป่าสุ่ม โดยสุ่มสร้างต้นไม้ขึ้นมาสักร้อยต้น
ได้
ค่าที่ได้ออกมานี้ก็คือค่าความสำคัญของตัวแปรแต่ละตัวตามลำดับ ลองเอามาวาดเป็นแผนภูมิแท่งแสดงเพื่อให้เห็นชัดได้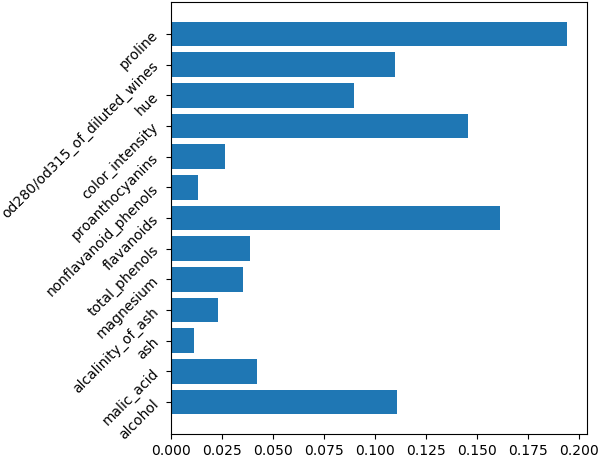
ทีนี้ลองเอาตัวแปรที่สำคัญสามอันดับแรกมาวาดกระจายในสามมิติดู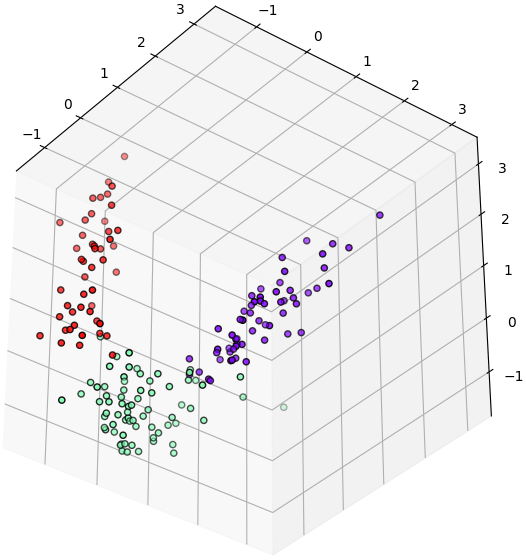
จะเห็นว่ามีการกระจายแบ่งเขตของทั้ง ๓ กลุ่มอย่างชัดเจน ซึ่งแสดงว่าแค่ใช้ ๓ ตัวแปรนี้เป็นตัวแบ่งก็สามารถแบ่งได้ดี
ในขณะที่หากลองเปลี่ยนเป็นวาดการกระจายของ ๓ กลุ่มที่ได้คะแนนน้อยที่สุดดู (แก้แค่บรรทัดแรก ที่เหลือเหมือนเดิม)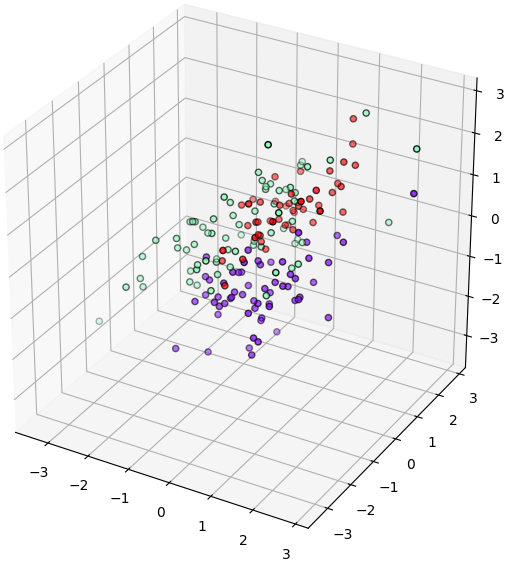
จะเห็นว่า ๓ กลุ่มปนเปกันแทบแยกออกจากกันไม่ได้
ต่อไปลองวาดกราฟเทียบดูว่าจำนวนตัวแปรที่ใช้จะมีผลต่อความแม่นยำของแบบจำลองแค่ไหน โดยตัวแปรในที่นี้เลือกเรียงตามลำดับคะแนนความสำคัญที่ได้มา คือถ้าใช้ตัวแปรตัวเดียวก็จะเลือกตัวที่มีความสำคัญสุด ถ้าเลือก ๒ ตัวก็หยิบตัวที่มีความสำคัญรองลงมามาใช้เพิ่ม ไล่ไปเรื่อยๆจนครบ ๑๓
ได้
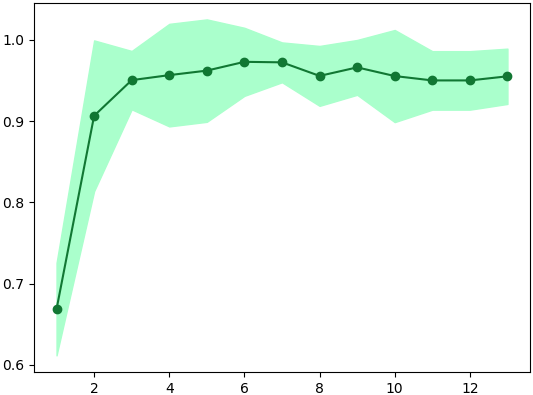
จากผลที่ได้ก็จะเห็นได้ว่าเมื่อใช้ตัวแปรแค่ ๖ หรือ ๗ ตัวแรกความแม่นยำที่ได้จะมากกว่าใช้ทั้ง ๑๓ ตัวเล็กน้อย
สรุปโดยรวมแล้วก็คือเมื่อทำการคัดตัวแปรที่เหมาะสมมาใช้ได้แล้ว ทีนี้ก็จะสามารถใช้ตัวแปรลดลง ลดมิติของปัญหา แบบจำลองก็ซับซ้อนน้อยลง การคำนวณก็ง่ายขึ้น แต่สามารถได้ความแม่นยำใกล้เคียงหรือมากขึ้นกว่าเดิมเล็กน้อย นี่คือความสำคัญของการคัดเลือกค่าแทนลักษณะ
นอกจากชุดข้อมูลภาพตัวเลขของ MNIST ที่เคยแนะนำไปแล้ว https://phyblas.hinaboshi.com/20170920
ก็ยังมีข้อมูลจำนวนหนึ่งที่มีขนาดเล็กๆและถูกเก็บอยู่ภายในตัวมอดูลอยู่แล้วจึงดึงข้อมูลมาใช้ได้ทันที
ในที่นี้จะลองใช้ข้อมูลหนึ่งในนั้นซึ่งนิยมใช้กันมาก คือชุดข้อมูลไวน์ (wine dataset)

ชุดข้อมูลไวน์ประกอบไปด้วยข้อมูลค่าที่บอกค่าคุณสมบัติต่างๆของไวน์ พร้อมกับบอกว่าเป็นไวน์ชนิดไหน โดยมีการแบ่งเป็น ๓ ชนิด จำนวนข้อมูลมีทั้งหมด ๑๗๘ แถว
ค่าคุณสมบัติต่างๆนั้นมีจำนวนมาก รวมแล้วมีถึง ๑๓ ชนิด นั่นคือเป็นปัญหาที่มีมิติสูงถึง ๑๓ มิติ
เพื่อให้เห็นภาพ ลองดึงข้อมูลมาดูเป็นตัวอย่างแล้วดูว่าข้างในเป็นยังไงบ้าง ข้อมูลอยู่ในแอตทริบิวต์ .data ส่วนเลขชนิดของไวน์อยู่ใน .target
from sklearn import datasets
wine = datasets.load_wine()
print(wine.data.shape) # ได้ (178, 13)
print(set(wine.target)) # ได้ {0, 1, 2}
print(wine.data[wine.target==0].shape) # ได้ (59, 13)
print(wine.data[wine.target==1].shape) # ได้ (71, 13)
print(wine.data[wine.target==2].shape) # ได้ (48, 13)ค่าต่างๆทั้ง ๑๓ นั้นคือค่าของอะไรบ้างสามารถเห็นได้จากในแอตทริบิวต์ .feature_names
print(wine.feature_names)
print(wine.data[0])ได้
['alcohol', 'malic_acid', 'ash', 'alcalinity_of_ash', 'magnesium', 'total_phenols', 'flavanoids', 'nonflavanoid_phenols', 'proanthocyanins', 'color_intensity', 'hue', 'od280/od315_of_diluted_wines', 'proline']
[ 1.42300000e+01 1.71000000e+00 2.43000000e+00 1.56000000e+01
1.27000000e+02 2.80000000e+00 3.06000000e+00 2.80000000e-01
2.29000000e+00 5.64000000e+00 1.04000000e+00 3.92000000e+00
1.06500000e+03]ทั้งหมดนี้คือคุณสมบัติที่จะเอามาใช้แบ่งชนิดของไวน์

เนื่องจากมีจำนวนมิติมาก จึงเหมาะที่จะถูกนำมาใช้เป็นตัวอย่างฝึกเรื่องการคัดเลือกค่าแทนลักษณะ (特征选择, feature selection) คือการเลือกว่าค่าคุณสมบัติอันไหนที่เป็นปัจจัยสำคัญในการทำให้คำตอบเปลี่ยนแปลงไปมากที่สุด
เพราะในจำนวนคุณสมบัติทั้ง ๑๓ อย่างนี้ ไม่ใช่ว่าแต่ละค่าจะสำคัญไปทั้งหมด อาจมีแค่บางค่าที่สำคัญเป็นพิเศษ แต่บางค่าอาจแทบไม่มีผลอะไรต่อคำตอบเลยก็เป็นได้
จริงอยู่ว่าพิจารณาปัจจัยต่างๆเยอะไว้ก่อนไม่เสียหาย แต่บางครั้งก็ทำให้แบบจำลองมีความซับซ้อนเกินไปจนเกิดการเรียนรู้เกินได้ อีกทั้งแน่นอนว่าตัวแปรเยอะก็ใช้เวลาคำนวณนานขึ้น ดังนั้นการพิจารณาลดมิติของปัญหาจึงมีความสำคัญเหมือนกัน
การคัดเลือกว่าคุณสมบัติไหนมีความสำคัญน่านำมาใช้นั้นมีอยู่หลายวิธีมาก ในที่นี้จะลองใช้วิธีการป่าสุ่ม ซึ่งเคยเขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20171117
สำหรับแบบจำลองที่จะใช้ในการแบ่ง คราวนี้ขอเลือกใช้วิธีการเพื่อนบ้านใกล้สุด k ตัวใน sklearn https://phyblas.hinaboshi.com/20171031
และเพื่อให้ผลออกมามั่นใจได้มากขึ้นจะใช้การตรวจสอบแบบไขว้โดยฟังก์ชัน cross_val_score รายละเอียดเขียนไว้ใน https://phyblas.hinaboshi.com/20171020
เริ่มจาก ลองหาค่าความแม่นยำของแบบจำลองโดยใช้ตัวแปรทั้งหมด ๑๓ ตัว
from sklearn.neighbors import KNeighborsClassifier as Knn
from sklearn.model_selection import cross_val_score as crovasco
wine = datasets.load_wine()
X,z = wine.data,wine.target
X = (X-X.mean(0))/X.std(0) # ปรับค่าตัวแปรต่างๆให้เป็นมาตรฐาน
khanaen = crovasco(Knn(),X,z,cv=5)
print('%.3f ± %.3f'%(khanaen.mean(),khanaen.std()))
# ได้ 0.955 ± 0.034Knn ในที่นี้ใช้ค่าตั้งต้นคือมีจำนวนเพื่อนบ้าน ๕ ตัว และใช้ cv=5 คือแบ่งข้อมูลเป็น ๕ ส่วนในการตรวจสอบแบบไขว้ ทำการคำนวณ ๕ ครั้ง หาความแม่นยำของทั้ง ๕ ครั้งแล้วเอามาเฉลี่ยกันพร้อมหาส่วนเบี่ยงเบนมาตรฐานด้วย
จากนั้นลองมาเร่ิมพิจารณาการลดมิติของปัญหาดูด้วยป่าสุ่ม โดยสุ่มสร้างต้นไม้ขึ้นมาสักร้อยต้น
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier as Rafo
np.random.seed(0)
rafo = Rafo(100)
rafo.fit(X,z)
print(rafo.feature_importances_)ได้
[ 0.15393774 0.03647811 0.01660083 0.03027144 0.03062104 0.04283046
0.16273435 0.00988292 0.02454873 0.12499868 0.09461291 0.1187603
0.15372249]ค่าที่ได้ออกมานี้ก็คือค่าความสำคัญของตัวแปรแต่ละตัวตามลำดับ ลองเอามาวาดเป็นแผนภูมิแท่งแสดงเพื่อให้เห็นชัดได้
plt.axes([0.3,0.05,0.65,0.9])
plt.barh(np.arange(13),rafo.feature_importances_)
plt.yticks(np.arange(13),wine.feature_names,rotation=45)
plt.show()
ทีนี้ลองเอาตัวแปรที่สำคัญสามอันดับแรกมาวาดกระจายในสามมิติดู
X3 = X[:,rafo.feature_importances_.argsort()[:-4:-1]]
plt.figure(figsize=[6,6])
minmax = X3.min(),X3.max()
ax = plt.axes([0,0,1,1],projection='3d',xlim=minmax,ylim=minmax,zlim=minmax)
ax.scatter(X3[:,0],X3[:,1],X3[:,2],c=z,edgecolor='k',cmap='rainbow')
plt.show()
จะเห็นว่ามีการกระจายแบ่งเขตของทั้ง ๓ กลุ่มอย่างชัดเจน ซึ่งแสดงว่าแค่ใช้ ๓ ตัวแปรนี้เป็นตัวแบ่งก็สามารถแบ่งได้ดี
ในขณะที่หากลองเปลี่ยนเป็นวาดการกระจายของ ๓ กลุ่มที่ได้คะแนนน้อยที่สุดดู (แก้แค่บรรทัดแรก ที่เหลือเหมือนเดิม)
X3 = X[:,rafo.feature_importances_.argsort()[:3]]
จะเห็นว่า ๓ กลุ่มปนเปกันแทบแยกออกจากกันไม่ได้
ต่อไปลองวาดกราฟเทียบดูว่าจำนวนตัวแปรที่ใช้จะมีผลต่อความแม่นยำของแบบจำลองแค่ไหน โดยตัวแปรในที่นี้เลือกเรียงตามลำดับคะแนนความสำคัญที่ได้มา คือถ้าใช้ตัวแปรตัวเดียวก็จะเลือกตัวที่มีความสำคัญสุด ถ้าเลือก ๒ ตัวก็หยิบตัวที่มีความสำคัญรองลงมามาใช้เพิ่ม ไล่ไปเรื่อยๆจนครบ ๑๓
riang = rafo.feature_importances_.argsort()[::-1]
khanaen = []
for i in range(1,14):
khanaen.append(crovasco(Knn(),X[:,riang[:i]],z,cv=5))
khanaen = np.array(khanaen)
mean = khanaen.mean(1)
std = khanaen.std(1)
plt.plot(np.arange(1,14),mean,'o-',color='#117733')
plt.fill_between(np.arange(1,14),mean-std,mean+std,color='#AAFFCC')
plt.show()
print(mean)ได้
array([ 0.66856033, 0.90644788, 0.95028314, 0.95645646, 0.96201201,
0.97282282, 0.97219573, 0.95550256, 0.96598657, 0.95532591,
0.94994701, 0.94994701])
จากผลที่ได้ก็จะเห็นได้ว่าเมื่อใช้ตัวแปรแค่ ๖ หรือ ๗ ตัวแรกความแม่นยำที่ได้จะมากกว่าใช้ทั้ง ๑๓ ตัวเล็กน้อย
สรุปโดยรวมแล้วก็คือเมื่อทำการคัดตัวแปรที่เหมาะสมมาใช้ได้แล้ว ทีนี้ก็จะสามารถใช้ตัวแปรลดลง ลดมิติของปัญหา แบบจำลองก็ซับซ้อนน้อยลง การคำนวณก็ง่ายขึ้น แต่สามารถได้ความแม่นยำใกล้เคียงหรือมากขึ้นกว่าเดิมเล็กน้อย นี่คือความสำคัญของการคัดเลือกค่าแทนลักษณะ
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> sklearn