[python] วิเคราะห์การถดถอยโดยใช้วิธีการเคอร์เนล
เขียนเมื่อ 2018/07/24 22:28
แก้ไขล่าสุด 2021/09/28 16:42
วิธีการเคอร์เนล (核方法, kernel method) หรือนิยมเรียกกันว่าลูกเล่นเคอร์เนล (核技巧, kernel trick) เป็นวิธีการที่ใช้อย่างกว้างขวางในเทคนิคการเรียนรู้ของเครื่อง
สำหรับบทความนี้จะมาอธิบายหลักการและการใช้วิธีการเคอร์เนลโดยละเอียด
หลักการ
การวิเคราะห์ปัญหาที่ไม่เป็นเชิงเส้นนั้นมีความซับซ้อน โดยทั่วไปหากสามารถเปลี่ยนปัญหาที่พิจารณาให้เป็นเชิงเส้นได้จะสามารถคิดอะไรๆได้ง่ายขึ้น
เช่นเมื่อพิจารณาความสัมพันธ์ระหว่างตัวแปรต้นและตัวแปรตามซึ่งมีความสัมพันธ์ที่ดูแล้วเป็นฟังก์ชันซับซ้อน แต่ถ้าเราใช้วิธีอะไรสักอย่างแปลงข้อมูลเหล่านี้ให้ไปอยู่ในปริภูมิอื่น มันอาจกลายเป็นเชิงเส้นขึ้นมาได้ มิติของปริภูมินั้นอาจสูงกว่า แต่ถ้าเป็นเชิงเส้นก็จะทำให้พิจารณาง่ายขึ้น
ภาพตัวอย่างคร่าวๆ ด้านบนคือปริภูมิเดิมของข้อมูลที่เราพิจารณาอยู่ตอนแรก ส่วนภาพล่างคือจุดข้อมูลเหล่านั้นภายในปริภูมิใหม่ สีเดียวกันกับด้านบนแสดงถึงจุดเดียวกันถูกแปลงมาเป็นจุดนั้นในด้านล่าง
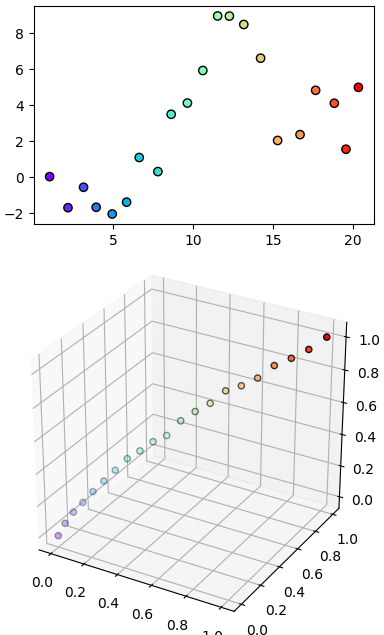
ในการใช้วิธีการเคอร์เนล ปริภูมิใหม่ที่ว่านี้เรียกว่าเป็นปริภูมิของเคอร์เนล ค่าในปริภูมิเคอร์เนลเป็นฟังก์ชันของจุดต่างๆในปริภูมิเดิม
ปริภูมิของเคอร์เนลที่ว่านี้ ถ้าจะพูดโดยละเอียดจริงๆก็คือเป็นปริภูมิชนิดที่เรียกว่า ปริภูมิฮิลแบร์ทเคอร์เนลเกิดซ้ำ (再生核希尔伯特空间, reproducing kernel Hilbert space)
อย่างไรก็ตามเรื่องนี้เป็นคณิตศาสตร์ระดับสูงเข้าใจยากพอสมควร เราไม่จำเป็นต้องลงลึกในรายละเอียดขนาดนั้นก็ได้ ให้เข้าใจว่าเป็นปริภูมิอะไรบางอย่างที่ต่างจากปริภูมิที่เราพิจารณาอยู่เดิม และการคำนวณในปริภูมินั้นทำให้การวิเคราะห์ข้อมูลสะดวกได้
วิธีการเคอร์เนลมีพื้นฐานมาจากการใช้ฟังก์ชันฐาน (基函数, basis function) ซึ่งเขียนถึงไปใน https://phyblas.hinaboshi.com/20180720
เนื้อหาในนี้จะต่อเนื่องจากพื้นฐานในบทความนั้น สมการต่างๆก็ยกมาจากในนั้นโดยอาจจะไม่ได้อธิบายซ้ำโดยละเอียดนัก ดังนั้นควรอ่านบทความนั้นมาก่อน
ปริภูมิเคอร์เนลได้จากการแปลงต่อมาจากปริภูมิของฟังก์ชันฐานลักษณะเฉพาะ ϕ อีกที
โดยนิยามฟังก์ชันใหม่ K เรียกว่าเป็นฟังก์ชันเคอร์เนล หรืออาจเรียกว่าเคอร์เนลเฉยๆ
..(1)
K เกิดจากผลคูณเวกเตอร์ ϕ ในปริภูมิของ ϕ หรือโดยทั่วไปมักเรียกว่าเป็นผลคูณภายใน (内积, inner product) ของปริภูมิ ϕ บางครั้งก็นิยมเขียนแทนด้วยกรอบลักษณะแบบนี้
..(2)
โดยทั่วไปถ้าปริภูมิ ϕ มีจำนวนมิติจำกัด เช่นมีจำนวนมิติ m มิติ ผลคูณภายในจะได้ว่า
..(3)
แต่ในวิธีการเคอร์เนลเรามักจะให้ ϕ มีจำนวนมิติเป็นอนันต์ ซึ่งผลคูณภายในจะเป็นการหาปริพันธ์แบบนี้
..(4)
มีมิติเป็นจำนวนอนันต์นี่เป็นยังไง คิดว่าอาจจะเป็นเรื่องที่จินตนาการได้ยาก ขอยกตัวอย่างฟังก์ชัน เช่นกรณีที่ฐาน ϕ เป็นฟังก์ชันเกาส์
..(5)
ในที่นี้ ξ จะหมายถึงจุดที่ใช้เป็นศูนย์กลาง ซึ่งตำแหน่งนี้อาจเป็นจุดใดๆบนปริภูมิของตัวแปรต้น x ดังนั้นจึงมีจำนวนเป็นอนันต์ จึงเรียกได้ว่าปริภูมิของ ϕ มีจำนวนมิติเป็นอนันต์
แบบนี้ผลคูณภายในจะกลายเป็น
..(6)
จะเห็นว่าเมื่อใช้ฟังก์ชันฐานเป็นฟังก์ชันเกาส์ ก็จะได้เคอร์เนลออกมาเป็นฟังก์ชันเกาส์ในลักษณะเดิม
เขียนเคอร์เนลเกาส์ใหม่ในรูปทั่วไปได้เป็น
..(7)
โดย
..(8)
โดย σ แสดงถึงขนาดความกว้าง ปกติฟังก์ชันโดยพื้นฐานแล้วจะถูกเขียนในรูป σ เพราะเห็นภาพชัดกว่า แต่เพื่อให้เขียนง่ายในที่นี้ใช้รูป γ
โดยทั่วไปเคอร์เนลเกาส์แบบนี้มักถูกเรียกว่า เคอร์เนลฟังก์ชันฐานแนวรัศมี (径向基函数核, Radial basis function kernel) และนิยมเรียกย่อๆว่า RBF
เพียงแต่ว่ากันในรายละเอียดจริงๆแล้ว RBF หมายถึงฟังก์ชันอะไรก็ได้ที่ใช้ฐานเป็นฟังก์ชันที่มีจุดศูนย์กลางและมีค่าเปลี่ยนแปลงตามระยะห่างจากใจกลาง ดังนั้นอาจไม่ใช่ฟังก์ชันเกาส์ เพียงแต่ปกติฟังก์ชันเกาส์ใช้กันทั่วไปมากที่สุด ดังนั้นพอพูดถึง RBF ก็จะหมายถึงฟังก์ชันเกาส์
นอกจากเคอร์เนลเกาส์แล้ว ยังมีเคอร์เนลชนิดอื่นที่อาจใช้ได้ เช่น เคอร์เนลลาปลาส เคอร์เนลพหุนาม เป็นต้น แต่ในที่นี้จะอธิบายโดยเน้นเคอร์เนลเกาส์เป็นหลัก
ในปัญหาการวิเคราะห์การถดถอยจะคำนวณเคอร์เนล K ระหว่างค่าใหม่ x ที่ต้องการหาค่ากับ x เก่าที่เป็นข้อมูลที่มี แล้วนำมาคำนวณ
..(9)
ในที่นี้เขียนห้อย B หมายถึงข้อมูลกลุ่มใหม่ที่ต้องการหาค่า ห้อย A หมายถึงกลุ่มเก่าซึ่งรู้ค่า z อยู่แล้วและใช้ในการเรียนรู้
ที่ใช้สัญลักษณ์เป็นเวกเตอร์ในที่นี้หมายถึงว่ามีข้อมูล x หลายตัว
อนึ่ง ในบทความนี้จะใช้อักษรตัวหนาแทนปริมาณที่เป็นเมทริกซ์สองมิติ ส่วนที่มีลูกศรด้านบนแทนปริมาณเวกเตอร์ ซึ่งถือเป็นเมทริกซ์หนึ่งมิติด้วย ส่วนอักษรตัวเอียงธรรมดาคือค่าเลขตัวเดียว
ถ้าแจกเป็นเมทริกซ์ให้เห็นภาพชัดจะได้แบบนี้
..(10)
โดย n เป็นจำนวนข้อมูลเก่า n' เป็นจำนวนข้อมูลกลุ่มใหม่
ค่าของแต่ละตัวจะได้เป็น
..(11)
โดย a คือค่าน้ำหนักของเคอร์เนลแต่ละตัว อาจมองว่าคล้ายกับค่าน้ำหนัก w ตอนใช้ฟังก์ชันฐานลักษณะเฉพาะก็ได้ แค่เปลี่ยนจากน้ำหนักของฟังก์ชันฐานมาเป็นน้ำหนักของเคอร์เนล
ค่า a คำนวณจากเคอร์เนลภายในตัวข้อมูลเก่าบวกกับเรกูลาไรซ์
..(12)
โดย λ คือขนาดของการเรกูลาไรซ์
ส่วนที่มาของค่า a ถ้าจะเข้าใจอาจต้องอธิบายย้อนกลับไปนิด
เดิมทีในการใช้ฟังก์ชันฐานลักษณะเฉพาะในการคำนวณนั้น เราจะอธิบายค่าของฟังก์ชัน z ที่เราต้องการหาในรูปของฟังก์ชันฐาน ϕ(x) คูณกับน้ำหนัก w
..(13)
เมื่อมีจุดข้อมูลอยู่หลายค่า ค่า x และ z ก็มีอยู่หลายตัว อาจแสดงได้ในรูปเมทริกซ์ดังนี้
..(14)
โดยในที่นี้ m เป็นจำนวนฐาน และ n เป็นจำนวนจุดข้อมูลที่ใช้
ค่าน้ำหนัก w นี้เป็นค่าที่ต้องคำนวณหาเอาจากข้อมูลค่า x และ z ที่ป้อนเข้าไปเป็นตัวอย่างข้อมูลสำหรับการเรียนรู้
จากเมทริกซ์ข้างต้นนี้จะได้ระบบสมการทั้งหมด n สมการ และมีค่าที่ต้องการหาคือ w ทั้งหมด m ตัว
โดยทั่วไปแล้วเวลาใช้ฟังก์ชันฐานในการคำนวณโดยทั่วไปจำนวนฐาน (m) จะน้อยกว่าจำนวนจุดข้อมูล (n) แสดงว่าจำนวนเงื่อนไขมีมากกว่าตัวแปรที่ต้องการหา กรณีแบบนี้ปกติจะไม่สามารถหา w ที่สอดคล้องกับจุดข้อมูลทั้งหมดได้
ดังนั้นเวลาแก้หาค่า w จะเป็นการหาโดยพิจารณาจากการทำให้ค่าความคลาดเคลื่อนต่ำสุด นั่นคือ
..(15)
แล้วก็จะได้ว่า
..(16)
แต่ในทางกลับกัน คราวนี้เราต้องการพิจารณากรณีที่ใช้ฐานจำนวนมากมาย มากกว่าจำนวนจุดข้อมูลที่มี (มากจนเป็นอนันต์) แบบนี้จะกลายเป็นว่าจำนวนสมการเงื่อนไขมีน้อยกว่าตัวแปรที่ต้องการหา กรณีนี้จะกลายเป็นว่าหาค่า w ได้ไม่จำกัด
ดังนั้นตรงนี้จะกลายมาเป็นปัญหาที่ว่าให้หาค่า w ที่มีขนาดต่ำสุด หรือก็คือผลรวมกำลังสองต่ำที่สุด
..(17)
การแก้หาค่าอาจทำโดยใช้ตัวคูณลากรองจ์ (拉格朗日乘数, Lagrange multipliers) สำหรับวิธีการจะขอละไว้ แต่ผลที่ได้จะออกมาเป็น
..(18)
จะเห็นว่าสมการ (16) กับ (18) อาจดูคล้ายกันแต่ก็ต่างกัน ที่สำคัญคือ ΦΦT จะได้เมทริกซ์ขนาด n×n ในขณะที่ ΦTΦ จะเป็นเมทริกซ์ขนาด m×m
ถ้านำ w ที่ได้จากตรงนี้ไปใช้เพื่อคำนวณหาค่า z ใหม่สำหรับค่า x ใหม่โดยใช้สมการ (14) จะได้ว่า
..(19)
และจะเห็นว่าฟังก์ชันฐานที่ปรากฏในนี้อยู่ในรูปของเวกเตอร์คูณกัน ซึ่งก็คือผลคูณภายใน ผลคูณภายในของฟังก์ชันฐานก็คือเคอร์เนล ดังนิยามในสมการ (1) ดังนั้นจะได้
..(20)
ซึ่งก็กลับไปสู่สมการ (11) แล้วก็จะได้ค่า a ตามสมการ (12)
จะเห็นว่า ϕ ทั้งหมดถูกเขียนในรูปของ K ได้หมด นั่นหมายความว่าเราไม่จำเป็นต้องคำนวณฟังก์ชัน ϕ โดยตรงแต่คำนวณ K ซึ่งเป็นผลคูณภายในของ ϕ
แนวคิดตรงนี้มีประโยชน์มาก เพราะเมื่อมีจำนวนฟังก์ชันฐานเยอะมาก แบบนั้นถ้าเราต้องมาคำนวณ ϕ ออกมาจำนวนขนาดนั้น ปริมาณการคำนวณจะหนักมาก
แต่พอกลายเป็นว่าแค่คำนวณเคอร์เนล K ก็พอแล้ว ไม่ต้องคำนวณ ϕ โดยตรงแล้ว ต่อให้จำนวนฐานมีมากแค่ไหน จำนวนฐานอาจมีมากถึงเป็นอนันต์ ก็ไม่ทำให้ต้องคำนวณหนัก
แค่คำนวณพารามิเตอร์เป็นจำนวนแค่เท่ากับจุดข้อมูลก็เสมือนกับว่าพิจารณาฐานที่มีจำนวนมิติเป็นอนันต์ได้แล้ว แบบนี้ดูแล้วเป็นกลยุทธ์ลูกเช่นที่ทำให้การคำนวณง่ายสบายมาก ก็เลยมักถูกเรียกว่าเป็นลูกเล่นเคอร์เนล
ลองเขียนสรุปลำดับการคำนวณแล้วก็จะออกมาแบบนี้
.*.
แต่ขั้นตอน Φ นั้นถูกละไปไม่ต้องคำนวณโดยตรง จาก x คำนวณ K เลย นี่คือวิธีการของลูกเล่นเคอร์เนล
โปรแกรม
เมื่อเข้าใจหลักการแล้วต่อมาลองเขียนโปรแกรมขึ้นมาดู
การคำนวณก็เป็นไปตามขั้นตอนนี้
1. คำนวณเคอร์เนล (K) ภายในตัวแปรต้นของข้อมูลที่จะเรียนรู้ (x)
2. ใช้ K และตัวแปรตามของข้อมูลที่จะเรียนรู้ (z) คำนวณค่าน้ำหนัก (a)
3. คำนวณเคอร์เนล (K_) ของข้อมูลที่ต้องการหาค่า (x_) และข้อมูลที่เรียนรู้ (x)
3. ใช้ K_ และ a คำนวณตัวแปรตามที่ต้องการหาค่า (z_) ของข้อมูลที่ต้องการหาค่า
ลองเขียนโค้ดได้แบบนี้
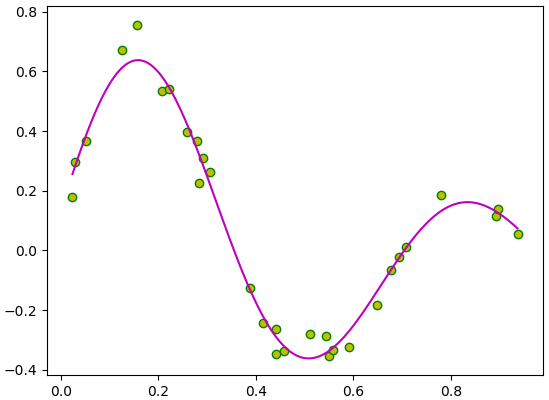
ต่อมาลองเขียนให้อยู่ในรูปของคลาส
ขอทดสอบการใช้ด้วยการลองเปรียบเทียบผลของพารามิเตอร์ γ และ λ ที่มีผลต่อค่าที่ได้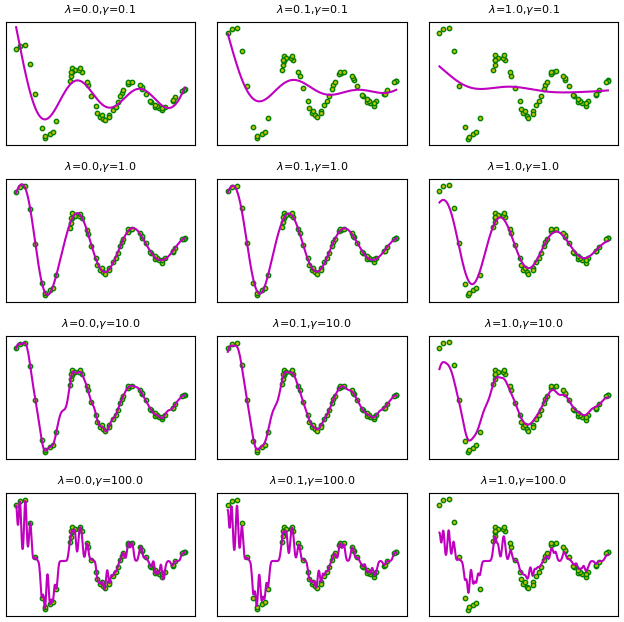
จะเห็นว่าผลที่ได้ต่างกันมาก ดังนั้นการเลือกค่าพารามิเตอร์ให้เหมาะสมจึงมีความสำคัญมาก
กรณีหลายตัวแปร
ในตัวอย่างที่อธิบายผ่านมาเป็นปัญหาที่มีตัวแปรต้นเพียงตัวเดียว (มิติเดียว) คือ x
แต่วิธีการเคอร์เนลสามารถประยุกต์ใช้กับข้อมูลที่มีตัวแปรต้นกี่ตัวก็ได้ ดังนั้นคราวนี้จะลองเปลี่ยนมาพิจารณากรณีหลายตัวแปร
ให้ข้อมูลตัวแปรต้นแทนด้วย
..(21)
ในที่นี้ตัวเลขห้อยมี ๒ ตัว ตัวแรกแทนว่าเป็นจุดที่เท่าไหร่ ตัวหลังแทนว่าเป็นมิติที่เท่าไหร่ แต่ถ้าห้อยตัวเดียวจะแค่แทนว่าเป็นจุดเท่าไหร่โดยเป็นเวกเตอร์แสดงค่าในทุกมิติของจุดนั้น
การคำนวณ Φ ก็เปลี่ยนเป็นใช้ค่าในแต่ละมิติมาร่วมคำนวณ แล้วเคอร์เนลก็คำนวณจาก Φ เหมือนเดิม
..(22)
..(23)
การคำนวณเคอร์เนลเกาส์จะกลายเป็นแบบนี้
..(24)
ที่เพิ่มเข้ามาคือการคำนวณระยะห่างจะต้องคิดหลายมิติแล้วมาบวกกัน
เขียนโค้ดใหม่ได้ดังนี้
หลักๆคือเปลี่ยนจากเดิมที่เป็นมิติเดียวมาเป็นหลายมิติ
นอกจากนี้ในที่นี้เปลี่ยนมาใช้ cdist ในการคำนวณระยะห่างตอนที่คำนวณเคอร์เนล ฟังก์ชันนี้นอกจากจะเขียนง่ายแล้วก็ยังเร็วด้วย
รายละเอียดเกี่ยวกับวิธีการใช้ฟังก์ชันนี้เขียนไว้ใน https://phyblas.hinaboshi.com/20180722
ลองนำมาใช้กับข้อมูลสองมิติดู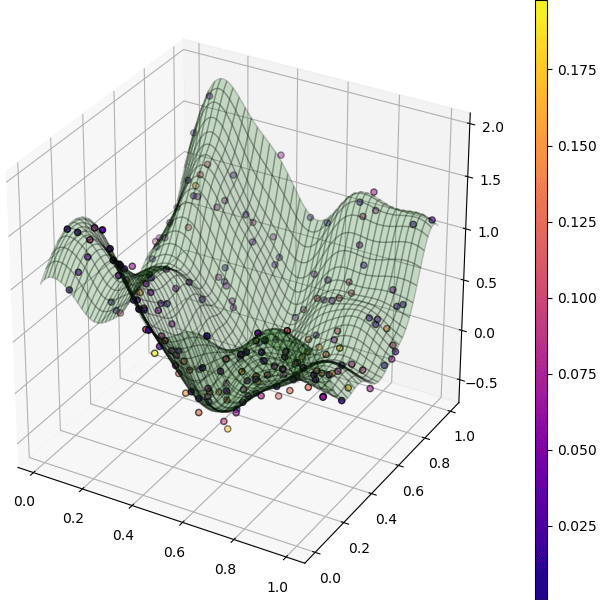
พื้นผิวคือค่า z ที่คำนวณได้ที่ x,y ค่าต่างๆ ส่วนจุดคือข้อมูลจริง
สีของจุดแสดงถึงความแตกต่างระหว่างค่า z จริงกับค่า z บนระนาบ
ทั้งหมดนี้เป็นหลักการพื้นฐานของลูกเล่นเคอร์เนล และการใช้ในการวิเคราะห์การถดถอย
แต่จริงๆแล้วแทนที่จะใช้ในการวิเคราะห์การถดถอย คนจำนวนมากทางสายการเรียนรู้ของเครื่องจะรู้จักลูกเล่นเคอร์เนลในฐานะเทคนิคที่ประยุกต์ใช้กับเทคนิคอื่นๆเช่น เครื่องเวกเตอร์ค้ำยัน (支持向量机, support vector machine, SVM) หรือ การวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) มากกว่า
สำหรับ SVM ได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20180709
ส่วน PCA เขียนไว้ใน https://phyblas.hinaboshi.com/20180727
อ้างอิง
สำหรับบทความนี้จะมาอธิบายหลักการและการใช้วิธีการเคอร์เนลโดยละเอียด
หลักการ
การวิเคราะห์ปัญหาที่ไม่เป็นเชิงเส้นนั้นมีความซับซ้อน โดยทั่วไปหากสามารถเปลี่ยนปัญหาที่พิจารณาให้เป็นเชิงเส้นได้จะสามารถคิดอะไรๆได้ง่ายขึ้น
เช่นเมื่อพิจารณาความสัมพันธ์ระหว่างตัวแปรต้นและตัวแปรตามซึ่งมีความสัมพันธ์ที่ดูแล้วเป็นฟังก์ชันซับซ้อน แต่ถ้าเราใช้วิธีอะไรสักอย่างแปลงข้อมูลเหล่านี้ให้ไปอยู่ในปริภูมิอื่น มันอาจกลายเป็นเชิงเส้นขึ้นมาได้ มิติของปริภูมินั้นอาจสูงกว่า แต่ถ้าเป็นเชิงเส้นก็จะทำให้พิจารณาง่ายขึ้น
ภาพตัวอย่างคร่าวๆ ด้านบนคือปริภูมิเดิมของข้อมูลที่เราพิจารณาอยู่ตอนแรก ส่วนภาพล่างคือจุดข้อมูลเหล่านั้นภายในปริภูมิใหม่ สีเดียวกันกับด้านบนแสดงถึงจุดเดียวกันถูกแปลงมาเป็นจุดนั้นในด้านล่าง

ในการใช้วิธีการเคอร์เนล ปริภูมิใหม่ที่ว่านี้เรียกว่าเป็นปริภูมิของเคอร์เนล ค่าในปริภูมิเคอร์เนลเป็นฟังก์ชันของจุดต่างๆในปริภูมิเดิม
ปริภูมิของเคอร์เนลที่ว่านี้ ถ้าจะพูดโดยละเอียดจริงๆก็คือเป็นปริภูมิชนิดที่เรียกว่า ปริภูมิฮิลแบร์ทเคอร์เนลเกิดซ้ำ (再生核希尔伯特空间, reproducing kernel Hilbert space)
อย่างไรก็ตามเรื่องนี้เป็นคณิตศาสตร์ระดับสูงเข้าใจยากพอสมควร เราไม่จำเป็นต้องลงลึกในรายละเอียดขนาดนั้นก็ได้ ให้เข้าใจว่าเป็นปริภูมิอะไรบางอย่างที่ต่างจากปริภูมิที่เราพิจารณาอยู่เดิม และการคำนวณในปริภูมินั้นทำให้การวิเคราะห์ข้อมูลสะดวกได้
วิธีการเคอร์เนลมีพื้นฐานมาจากการใช้ฟังก์ชันฐาน (基函数, basis function) ซึ่งเขียนถึงไปใน https://phyblas.hinaboshi.com/20180720
เนื้อหาในนี้จะต่อเนื่องจากพื้นฐานในบทความนั้น สมการต่างๆก็ยกมาจากในนั้นโดยอาจจะไม่ได้อธิบายซ้ำโดยละเอียดนัก ดังนั้นควรอ่านบทความนั้นมาก่อน
ปริภูมิเคอร์เนลได้จากการแปลงต่อมาจากปริภูมิของฟังก์ชันฐานลักษณะเฉพาะ ϕ อีกที
โดยนิยามฟังก์ชันใหม่ K เรียกว่าเป็นฟังก์ชันเคอร์เนล หรืออาจเรียกว่าเคอร์เนลเฉยๆ
..(1)
K เกิดจากผลคูณเวกเตอร์ ϕ ในปริภูมิของ ϕ หรือโดยทั่วไปมักเรียกว่าเป็นผลคูณภายใน (内积, inner product) ของปริภูมิ ϕ บางครั้งก็นิยมเขียนแทนด้วยกรอบลักษณะแบบนี้
..(2)
โดยทั่วไปถ้าปริภูมิ ϕ มีจำนวนมิติจำกัด เช่นมีจำนวนมิติ m มิติ ผลคูณภายในจะได้ว่า
..(3)
แต่ในวิธีการเคอร์เนลเรามักจะให้ ϕ มีจำนวนมิติเป็นอนันต์ ซึ่งผลคูณภายในจะเป็นการหาปริพันธ์แบบนี้
..(4)
มีมิติเป็นจำนวนอนันต์นี่เป็นยังไง คิดว่าอาจจะเป็นเรื่องที่จินตนาการได้ยาก ขอยกตัวอย่างฟังก์ชัน เช่นกรณีที่ฐาน ϕ เป็นฟังก์ชันเกาส์
..(5)
ในที่นี้ ξ จะหมายถึงจุดที่ใช้เป็นศูนย์กลาง ซึ่งตำแหน่งนี้อาจเป็นจุดใดๆบนปริภูมิของตัวแปรต้น x ดังนั้นจึงมีจำนวนเป็นอนันต์ จึงเรียกได้ว่าปริภูมิของ ϕ มีจำนวนมิติเป็นอนันต์
แบบนี้ผลคูณภายในจะกลายเป็น
..(6)
จะเห็นว่าเมื่อใช้ฟังก์ชันฐานเป็นฟังก์ชันเกาส์ ก็จะได้เคอร์เนลออกมาเป็นฟังก์ชันเกาส์ในลักษณะเดิม
เขียนเคอร์เนลเกาส์ใหม่ในรูปทั่วไปได้เป็น
..(7)
โดย
..(8)
โดย σ แสดงถึงขนาดความกว้าง ปกติฟังก์ชันโดยพื้นฐานแล้วจะถูกเขียนในรูป σ เพราะเห็นภาพชัดกว่า แต่เพื่อให้เขียนง่ายในที่นี้ใช้รูป γ
โดยทั่วไปเคอร์เนลเกาส์แบบนี้มักถูกเรียกว่า เคอร์เนลฟังก์ชันฐานแนวรัศมี (径向基函数核, Radial basis function kernel) และนิยมเรียกย่อๆว่า RBF
เพียงแต่ว่ากันในรายละเอียดจริงๆแล้ว RBF หมายถึงฟังก์ชันอะไรก็ได้ที่ใช้ฐานเป็นฟังก์ชันที่มีจุดศูนย์กลางและมีค่าเปลี่ยนแปลงตามระยะห่างจากใจกลาง ดังนั้นอาจไม่ใช่ฟังก์ชันเกาส์ เพียงแต่ปกติฟังก์ชันเกาส์ใช้กันทั่วไปมากที่สุด ดังนั้นพอพูดถึง RBF ก็จะหมายถึงฟังก์ชันเกาส์
นอกจากเคอร์เนลเกาส์แล้ว ยังมีเคอร์เนลชนิดอื่นที่อาจใช้ได้ เช่น เคอร์เนลลาปลาส เคอร์เนลพหุนาม เป็นต้น แต่ในที่นี้จะอธิบายโดยเน้นเคอร์เนลเกาส์เป็นหลัก
ในปัญหาการวิเคราะห์การถดถอยจะคำนวณเคอร์เนล K ระหว่างค่าใหม่ x ที่ต้องการหาค่ากับ x เก่าที่เป็นข้อมูลที่มี แล้วนำมาคำนวณ
..(9)
ในที่นี้เขียนห้อย B หมายถึงข้อมูลกลุ่มใหม่ที่ต้องการหาค่า ห้อย A หมายถึงกลุ่มเก่าซึ่งรู้ค่า z อยู่แล้วและใช้ในการเรียนรู้
ที่ใช้สัญลักษณ์เป็นเวกเตอร์ในที่นี้หมายถึงว่ามีข้อมูล x หลายตัว
อนึ่ง ในบทความนี้จะใช้อักษรตัวหนาแทนปริมาณที่เป็นเมทริกซ์สองมิติ ส่วนที่มีลูกศรด้านบนแทนปริมาณเวกเตอร์ ซึ่งถือเป็นเมทริกซ์หนึ่งมิติด้วย ส่วนอักษรตัวเอียงธรรมดาคือค่าเลขตัวเดียว
ถ้าแจกเป็นเมทริกซ์ให้เห็นภาพชัดจะได้แบบนี้
..(10)
โดย n เป็นจำนวนข้อมูลเก่า n' เป็นจำนวนข้อมูลกลุ่มใหม่
ค่าของแต่ละตัวจะได้เป็น
..(11)
โดย a คือค่าน้ำหนักของเคอร์เนลแต่ละตัว อาจมองว่าคล้ายกับค่าน้ำหนัก w ตอนใช้ฟังก์ชันฐานลักษณะเฉพาะก็ได้ แค่เปลี่ยนจากน้ำหนักของฟังก์ชันฐานมาเป็นน้ำหนักของเคอร์เนล
ค่า a คำนวณจากเคอร์เนลภายในตัวข้อมูลเก่าบวกกับเรกูลาไรซ์
..(12)
โดย λ คือขนาดของการเรกูลาไรซ์
ส่วนที่มาของค่า a ถ้าจะเข้าใจอาจต้องอธิบายย้อนกลับไปนิด
เดิมทีในการใช้ฟังก์ชันฐานลักษณะเฉพาะในการคำนวณนั้น เราจะอธิบายค่าของฟังก์ชัน z ที่เราต้องการหาในรูปของฟังก์ชันฐาน ϕ(x) คูณกับน้ำหนัก w
..(13)
เมื่อมีจุดข้อมูลอยู่หลายค่า ค่า x และ z ก็มีอยู่หลายตัว อาจแสดงได้ในรูปเมทริกซ์ดังนี้
..(14)
โดยในที่นี้ m เป็นจำนวนฐาน และ n เป็นจำนวนจุดข้อมูลที่ใช้
ค่าน้ำหนัก w นี้เป็นค่าที่ต้องคำนวณหาเอาจากข้อมูลค่า x และ z ที่ป้อนเข้าไปเป็นตัวอย่างข้อมูลสำหรับการเรียนรู้
จากเมทริกซ์ข้างต้นนี้จะได้ระบบสมการทั้งหมด n สมการ และมีค่าที่ต้องการหาคือ w ทั้งหมด m ตัว
โดยทั่วไปแล้วเวลาใช้ฟังก์ชันฐานในการคำนวณโดยทั่วไปจำนวนฐาน (m) จะน้อยกว่าจำนวนจุดข้อมูล (n) แสดงว่าจำนวนเงื่อนไขมีมากกว่าตัวแปรที่ต้องการหา กรณีแบบนี้ปกติจะไม่สามารถหา w ที่สอดคล้องกับจุดข้อมูลทั้งหมดได้
ดังนั้นเวลาแก้หาค่า w จะเป็นการหาโดยพิจารณาจากการทำให้ค่าความคลาดเคลื่อนต่ำสุด นั่นคือ
..(15)
แล้วก็จะได้ว่า
..(16)
แต่ในทางกลับกัน คราวนี้เราต้องการพิจารณากรณีที่ใช้ฐานจำนวนมากมาย มากกว่าจำนวนจุดข้อมูลที่มี (มากจนเป็นอนันต์) แบบนี้จะกลายเป็นว่าจำนวนสมการเงื่อนไขมีน้อยกว่าตัวแปรที่ต้องการหา กรณีนี้จะกลายเป็นว่าหาค่า w ได้ไม่จำกัด
ดังนั้นตรงนี้จะกลายมาเป็นปัญหาที่ว่าให้หาค่า w ที่มีขนาดต่ำสุด หรือก็คือผลรวมกำลังสองต่ำที่สุด
..(17)
การแก้หาค่าอาจทำโดยใช้ตัวคูณลากรองจ์ (拉格朗日乘数, Lagrange multipliers) สำหรับวิธีการจะขอละไว้ แต่ผลที่ได้จะออกมาเป็น
..(18)
จะเห็นว่าสมการ (16) กับ (18) อาจดูคล้ายกันแต่ก็ต่างกัน ที่สำคัญคือ ΦΦT จะได้เมทริกซ์ขนาด n×n ในขณะที่ ΦTΦ จะเป็นเมทริกซ์ขนาด m×m
ถ้านำ w ที่ได้จากตรงนี้ไปใช้เพื่อคำนวณหาค่า z ใหม่สำหรับค่า x ใหม่โดยใช้สมการ (14) จะได้ว่า
..(19)
และจะเห็นว่าฟังก์ชันฐานที่ปรากฏในนี้อยู่ในรูปของเวกเตอร์คูณกัน ซึ่งก็คือผลคูณภายใน ผลคูณภายในของฟังก์ชันฐานก็คือเคอร์เนล ดังนิยามในสมการ (1) ดังนั้นจะได้
..(20)
ซึ่งก็กลับไปสู่สมการ (11) แล้วก็จะได้ค่า a ตามสมการ (12)
จะเห็นว่า ϕ ทั้งหมดถูกเขียนในรูปของ K ได้หมด นั่นหมายความว่าเราไม่จำเป็นต้องคำนวณฟังก์ชัน ϕ โดยตรงแต่คำนวณ K ซึ่งเป็นผลคูณภายในของ ϕ
แนวคิดตรงนี้มีประโยชน์มาก เพราะเมื่อมีจำนวนฟังก์ชันฐานเยอะมาก แบบนั้นถ้าเราต้องมาคำนวณ ϕ ออกมาจำนวนขนาดนั้น ปริมาณการคำนวณจะหนักมาก
แต่พอกลายเป็นว่าแค่คำนวณเคอร์เนล K ก็พอแล้ว ไม่ต้องคำนวณ ϕ โดยตรงแล้ว ต่อให้จำนวนฐานมีมากแค่ไหน จำนวนฐานอาจมีมากถึงเป็นอนันต์ ก็ไม่ทำให้ต้องคำนวณหนัก
แค่คำนวณพารามิเตอร์เป็นจำนวนแค่เท่ากับจุดข้อมูลก็เสมือนกับว่าพิจารณาฐานที่มีจำนวนมิติเป็นอนันต์ได้แล้ว แบบนี้ดูแล้วเป็นกลยุทธ์ลูกเช่นที่ทำให้การคำนวณง่ายสบายมาก ก็เลยมักถูกเรียกว่าเป็นลูกเล่นเคอร์เนล
ลองเขียนสรุปลำดับการคำนวณแล้วก็จะออกมาแบบนี้
.*.
แต่ขั้นตอน Φ นั้นถูกละไปไม่ต้องคำนวณโดยตรง จาก x คำนวณ K เลย นี่คือวิธีการของลูกเล่นเคอร์เนล
โปรแกรม
เมื่อเข้าใจหลักการแล้วต่อมาลองเขียนโปรแกรมขึ้นมาดู
การคำนวณก็เป็นไปตามขั้นตอนนี้
1. คำนวณเคอร์เนล (K) ภายในตัวแปรต้นของข้อมูลที่จะเรียนรู้ (x)
2. ใช้ K และตัวแปรตามของข้อมูลที่จะเรียนรู้ (z) คำนวณค่าน้ำหนัก (a)
3. คำนวณเคอร์เนล (K_) ของข้อมูลที่ต้องการหาค่า (x_) และข้อมูลที่เรียนรู้ (x)
3. ใช้ K_ และ a คำนวณตัวแปรตามที่ต้องการหาค่า (z_) ของข้อมูลที่ต้องการหาค่า
ลองเขียนโค้ดได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
def gauss(x1,x2):
return np.exp(-gamma*(x1-x2)**2)
np.random.seed(3)
n = 30
x = np.random.uniform(0,1,n) # จุดข้อมูลที่ใช้เรียนรู้
z = np.sin(x*9)*np.exp(-2*x)+np.random.normal(0,0.04,n)
gamma = 10 # γ
l = 0.02 # λ
K = gauss(x[:,None],x)
a = np.linalg.solve(K+np.eye(n)*l,z)
x_ = np.linspace(x.min(),x.max(),401) # จุดที่ต้องการหาค่า
K_ = gauss(x_[:,None],x)
z_ = K_.dot(a)
plt.scatter(x,z,c='y',edgecolor='g')
plt.plot(x_,z_,'m')
plt.show()
ต่อมาลองเขียนให้อยู่ในรูปของคลาส
class ThotthoiKernel:
def __init__(self,gamma=1,l=0.1):
self.gamma = gamma
self.l = l
def rianru(self,x,z):
self.x = x
self.K = self.kernel(x[:,None],x)
self.a = np.linalg.solve(self.K+np.eye(len(z))*self.l,z)
def thamnai(self,x_):
K_ = self.kernel(x_[:,None],self.x)
return K_.dot(self.a)
def kernel(self,x1,x2):
return np.exp(-self.gamma*((x1-x2)**2))ขอทดสอบการใช้ด้วยการลองเปรียบเทียบผลของพารามิเตอร์ γ และ λ ที่มีผลต่อค่าที่ได้
n = 60
x = np.random.uniform(0,10,n)
z = np.sin(x*2)*np.exp(-0.2*x)*np.random.normal(1,0.1,n)
x_ = np.linspace(x.min(),x.max(),501)
plt.figure(figsize=[6.5,7])
for i,l in enumerate([0.01,0.1,1]):
for j,g in enumerate([0.1,1,10,100]):
tt = ThotthoiKernel(gamma=g,l=l)
tt.rianru(x,z)
z_ = tt.thamnai(x_)
plt.subplot2grid((4,3),(j,i),xticks=[],yticks=[])
plt.plot(x_,z_,'m')
plt.scatter(x,z,s=10,c='y',edgecolor='g')
plt.title('$\\lambda$=%.1f,$\\gamma$=%.1f'%(l,g),size=8)
plt.tight_layout()
plt.show()
จะเห็นว่าผลที่ได้ต่างกันมาก ดังนั้นการเลือกค่าพารามิเตอร์ให้เหมาะสมจึงมีความสำคัญมาก
กรณีหลายตัวแปร
ในตัวอย่างที่อธิบายผ่านมาเป็นปัญหาที่มีตัวแปรต้นเพียงตัวเดียว (มิติเดียว) คือ x
แต่วิธีการเคอร์เนลสามารถประยุกต์ใช้กับข้อมูลที่มีตัวแปรต้นกี่ตัวก็ได้ ดังนั้นคราวนี้จะลองเปลี่ยนมาพิจารณากรณีหลายตัวแปร
ให้ข้อมูลตัวแปรต้นแทนด้วย
..(21)
ในที่นี้ตัวเลขห้อยมี ๒ ตัว ตัวแรกแทนว่าเป็นจุดที่เท่าไหร่ ตัวหลังแทนว่าเป็นมิติที่เท่าไหร่ แต่ถ้าห้อยตัวเดียวจะแค่แทนว่าเป็นจุดเท่าไหร่โดยเป็นเวกเตอร์แสดงค่าในทุกมิติของจุดนั้น
การคำนวณ Φ ก็เปลี่ยนเป็นใช้ค่าในแต่ละมิติมาร่วมคำนวณ แล้วเคอร์เนลก็คำนวณจาก Φ เหมือนเดิม
..(22)
..(23)
การคำนวณเคอร์เนลเกาส์จะกลายเป็นแบบนี้
..(24)
ที่เพิ่มเข้ามาคือการคำนวณระยะห่างจะต้องคิดหลายมิติแล้วมาบวกกัน
เขียนโค้ดใหม่ได้ดังนี้
from scipy.spatial.distance import cdist
class ThotthoiKernel:
def __init__(self,gamma=1,l=0.1):
self.gamma = gamma
self.l = l
def rianru(self,X,z):
self.X = X
self.K = self.kernel(X,X)
self.a = np.linalg.solve(self.K+np.eye(len(z))*self.l,z)
def thamnai(self,X_):
K_ = self.kernel(X_,self.X)
return K_.dot(self.a)
def kernel(self,X1,X2):
return np.exp(-self.gamma*(cdist(X1,X2,'sqeuclidean')))หลักๆคือเปลี่ยนจากเดิมที่เป็นมิติเดียวมาเป็นหลายมิติ
นอกจากนี้ในที่นี้เปลี่ยนมาใช้ cdist ในการคำนวณระยะห่างตอนที่คำนวณเคอร์เนล ฟังก์ชันนี้นอกจากจะเขียนง่ายแล้วก็ยังเร็วด้วย
รายละเอียดเกี่ยวกับวิธีการใช้ฟังก์ชันนี้เขียนไว้ใน https://phyblas.hinaboshi.com/20180722
ลองนำมาใช้กับข้อมูลสองมิติดู
from mpl_toolkits.mplot3d import Axes3D
n = 200
X = np.random.random([n,2])
x,y = X.T
z = np.sin(x*9)*np.exp(-2*x)+np.random.normal(0,0.1,n)+5*(y-0.5)**2
gamma = 30
l = 0.01
tt = ThotthoiKernel(gamma=gamma,l=l)
tt.rianru(X,z)
mx,my = np.meshgrid(np.linspace(x.min(),x.max(),201),np.linspace(y.min(),y.max(),201))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = tt.thamnai(mX).reshape(201,-1)
ax = plt.figure(figsize=[7,6]).add_axes([0,0,1,1],projection='3d')
c = np.abs(z-tt.thamnai(X))
sc = ax.scatter(x,y,z,c=c,edgecolor='k',cmap='plasma')
ax.plot_surface(mx,my,mz,alpha=0.2,color='g',edgecolor='k')
plt.colorbar(sc,pad=0.01,aspect=50)
plt.show()
พื้นผิวคือค่า z ที่คำนวณได้ที่ x,y ค่าต่างๆ ส่วนจุดคือข้อมูลจริง
สีของจุดแสดงถึงความแตกต่างระหว่างค่า z จริงกับค่า z บนระนาบ
ทั้งหมดนี้เป็นหลักการพื้นฐานของลูกเล่นเคอร์เนล และการใช้ในการวิเคราะห์การถดถอย
แต่จริงๆแล้วแทนที่จะใช้ในการวิเคราะห์การถดถอย คนจำนวนมากทางสายการเรียนรู้ของเครื่องจะรู้จักลูกเล่นเคอร์เนลในฐานะเทคนิคที่ประยุกต์ใช้กับเทคนิคอื่นๆเช่น เครื่องเวกเตอร์ค้ำยัน (支持向量机, support vector machine, SVM) หรือ การวิเคราะห์องค์ประกอบหลัก (主成分分析, principle component Analysis, PCA) มากกว่า
สำหรับ SVM ได้เขียนถึงไปแล้วใน https://phyblas.hinaboshi.com/20180709
ส่วน PCA เขียนไว้ใน https://phyblas.hinaboshi.com/20180727
อ้างอิง
https://qiita.com/NoriakiOshita/items/138c10eada03938fcd79
https://qiita.com/kilometer/items/66e6116cc661019ead59
https://qiita.com/kilometer/items/58376b9a103743329b2f
https://qiita.com/kilometer/items/82924863daba6795a981
https://qiita.com/wsuzume/items/09a59036c8944fd563ff
https://qiita.com/takseki/items/de67bd7cc6bd800ab764
https://www.hellocybernetics.tech/entry/2016/08/09/051355
http://d.hatena.ne.jp/hgshrs/20130331/1364707361
http://kenichia.hatenablog.com/entry/2017/05/16/200019
http://www.ism.ac.jp/%7Efukumizu/OsakaU2014/OsakaU_1intro.pdf
http://www.ism.ac.jp/~fukumizu/papers/Nagoya_Nov2005.pdf
https://www.slideshare.net/yokkuns/tokyor45
https://www.slideshare.net/wosugi/ss-79624897
http://ibisml.org/archive/ibis2012/ibis2012-fukumizu.pdf
https://medium.com/@chih.sheng.huang821/機器學習-kernel-函數-47c94095171
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1618-03.pdf
https://qiita.com/kilometer/items/66e6116cc661019ead59
https://qiita.com/kilometer/items/58376b9a103743329b2f
https://qiita.com/kilometer/items/82924863daba6795a981
https://qiita.com/wsuzume/items/09a59036c8944fd563ff
https://qiita.com/takseki/items/de67bd7cc6bd800ab764
https://www.hellocybernetics.tech/entry/2016/08/09/051355
http://d.hatena.ne.jp/hgshrs/20130331/1364707361
http://kenichia.hatenablog.com/entry/2017/05/16/200019
http://www.ism.ac.jp/%7Efukumizu/OsakaU2014/OsakaU_1intro.pdf
http://www.ism.ac.jp/~fukumizu/papers/Nagoya_Nov2005.pdf
https://www.slideshare.net/yokkuns/tokyor45
https://www.slideshare.net/wosugi/ss-79624897
http://ibisml.org/archive/ibis2012/ibis2012-fukumizu.pdf
https://medium.com/@chih.sheng.huang821/機器學習-kernel-函數-47c94095171
http://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1618-03.pdf
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib