วิเคราะห์จำแนกประเภทข้อมูลด้วยเครื่องเวกเตอร์ค้ำยัน (SVM)
เขียนเมื่อ 2018/07/09 21:25
แก้ไขล่าสุด 2025/12/23 04:39
เครื่องเวกเตอร์ค้ำยัน (支持向量机, support vector machine) หรือ SVM เป็นเทคนิคการเรียนรู้ของเครื่องแบบนึงที่ได้รับความนิยมใช้กันอย่างกว้างขวาง
ในบทความนี้จะแนะนำตั้งแต่หลักการทำงานพื้นฐานของ SVM และวิธีคำนวณ ไปจนถึงการเขียนโค้ดไพธอนเพื่อสร้างโปรแกรมสำหรับจำแนกประเภทข้อมูลอย่างง่าย
หลักการทั่วไป
SVM เป็นการเรียนรู้ของเครื่องแบบมีผู้สอนซึ่งใช้ในการจำแนกประเภทข้อมูลออกเป็น ๒ กลุ่มโดยการหาเส้นกั้น
หลักการพื้นฐานนี้ใกล้เคียงกับการถดถอยโลจิสติก (逻辑回归, logistic regression)
อย่างไรก็ตาม SVM มีแนวคิดที่ซับซ้อนกว่า หากยังไม่เข้าใจการถดถอยโลจิสติกก็ยากที่จะเข้าใจ SVM ได้ ดังนั้นบทความนี้จะเขียนโดยถือว่าเป็นการต่อยอดจากเนื้อหาเรื่องการถดถอยโลจิสติก
ดังนั้นขอแนะนำให้อ่านบทความนี้ก่อน >> https://phyblas.hinaboshi.com/20161103
ในการถดถอยโลจิสติกนั้นหลักการหาเส้นแบ่งคั่นจะทำโดยการคำนวณค่าเสียหายจากฟังก์ชันซิกมอยด์ และพยายามทำให้ค่าเสียหายนั้นน้อยที่สุด
แต่สำหรับ SVM แล้วสิ่งที่ใช้พิจารณาในการแบ่งก็คือการหาช่องว่างที่จะทำให้ทั้ง ๒ กลุ่มแยกห่างออกจากกันมากที่สุด สร้างช่องว่างระหว่าง ๒ กลุ่มให้มากที่สุด
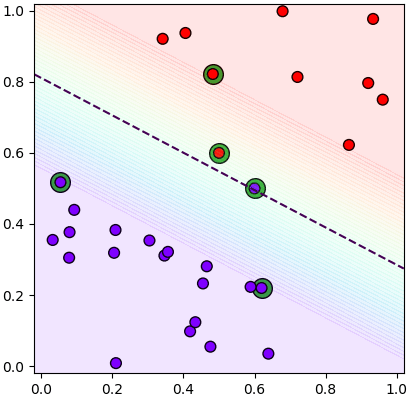
ช่องว่างที่ว่านี้ถูกเรียกว่าขอบกั้น แสดงด้วยสีรุ้งในภาพนี้ ส่วนเส้นประคือกึ่งกลาง
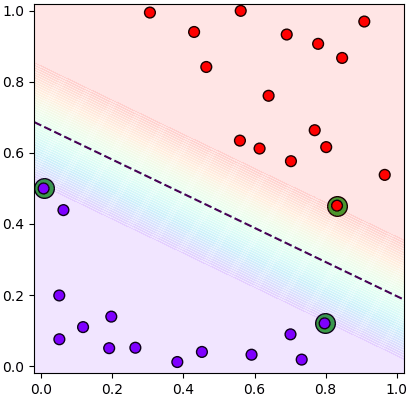
จะเห็นว่ามีไม่มีจุดไหนเลยอยู่ในบริเวณขอบกั้น แต่จะมีบางจุดที่อยู่ตรงขอบกั้นพอดี ซึ่งแสดงเป็นวงล้อมสีเขียวในภาพนี้
พวกจุดที่ตั้งอยู่บนขอบกั้นนี้จะถูกเรียกว่าเวกเตอร์ค้ำยัน (支持向量, support vector) ซึ่งเป็นที่มาของชื่อวิธีการนั่นเอง จุดเหล่านี้ทำหน้าที่ค้ำยันขอบกั้นที่แบ่งระหว่าง ๒ กลุ่ม
จากในภาพที่เห็นนี้จะเห็นว่ามีเวกเตอร์ค้ำยันอยู่ ๓ จุด แต่จริงๆแล้วในทางปฏิบัติอาจมีกี่จุดก็ได้ ซึ่งจะกล่าวถึงต่อไป
อย่างไรก็ตามในบางกรณีข้อมูลก็มีความคลาดเคลื่อนผิดพลาดจนทำให้มีการซ้อนเกี่ยวปนกันบ้างทำให้ไม่อาจแยกให้มีช่องว่างแบบนี้ได้ เช่นแบบนี้
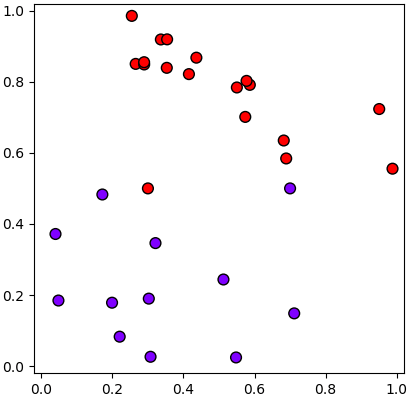
ดังนั้นโดยทั่วไปแล้วจึงมีการอลุ่มอล่วยให้มีข้อมูลบางส่วนสามารถอยู่ในขอบได้ แบบนี้
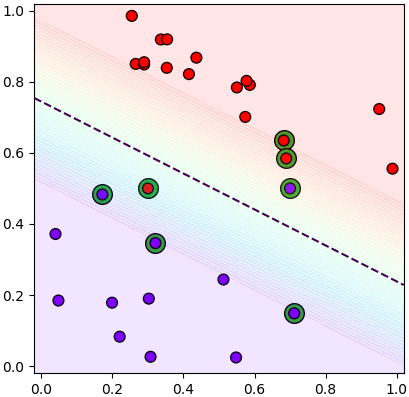
กรณีขอบที่มีการอลุ่มอล่วยแบบนี้จะเรียกว่าขอบนุ่ม (软间隔, soft margin) ส่วนแบบที่ไม่ยอมให้มีอะไรอยู่ที่ขอบเลยจะเรียกว่าขอบเข็ง (硬间隔, hard margin)
ขอบนุ่มมักจะหนา และขอบแข็งมักจะบาง หนานุ่มบางแข็ง (กรอบ) เช่นเดียวกับพิซซา ดังนั้นนึกภาพพิซซาตามอาจจะทำให้เห็นภาพง่ายขึ้นได้บ้าง แม้จะไม่เกี่ยวข้องกันโดยตรงก็ตาม
ภาพพิซซาหนานุ่มและบางกรอบ

ลองดูสองภาพนี้ เทียบกันจะเห็นว่าทำขอบนุ่มสักหน่อยดูแล้วแบ่งได้สมเหตุสมผลขึ้นดีกว่าทู่ซี้จะแบ่งแบบขอบแข็ง แม้ว่าจะแบ่งได้ก็ตาม
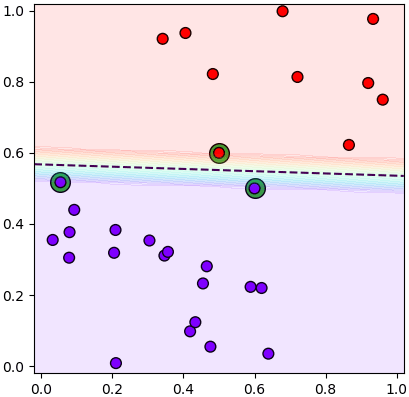
ดังนั้นการทำขอบนุ่มจึงเป็นการป้อนกันการเรียนรู้เกิน หลักการใกล้เคียงกับการเรกูลาไรซ์ของการถดถอยโลจิสติก ดังที่เขียนไปใน https://phyblas.hinaboshi.com/20170928
และจะเห็นว่าขอบนุ่มมีแนวโน้มจะใช้เวกเตอร์ค้ำยันเยอะกว่า
ขอบนุ่มก็มีระดับความนุ่มอยู่ ซึ่งมักกำหนดด้วยพารามิเตอร์ C ซึ่งจะกล่าวถึงรายละเอียดต่อไปภายหลัง ยิ่ง C มีค่าน้อยขอบก็ยิ่งหนานุ่ม แต่ถ้า C มากจนเป็นอนันต์ก็จะเป็นขอบแข็ง
ขอบจะนุ่มหรือแข็งแค่ไหนถึงจะดีก็แล้วแต่ข้อมูลที่พิจารณา ไม่มีคำตอบตายตัว เหมือนกับพิซซา จะเลือกกินขอบหนานุ่มหรือบางกรอบก็แล้วแต่คน
การหาขอบแบ่ง
เมื่อรู้เป้าหมายว่าต้องหาเส้นแบ่งแล้ว ต่อไปก็คือจะหาเส้นแบ่งอย่างไรดี ว่าหลักการมาฟังดูเหมือนจะง่าย แต่พอคิดจะทำจริงๆแล้วไม่ใช่เรื่องง่ายอย่างที่คิด
SVM นั้นจะมีการสร้างฟังก์ชันเชิงเส้นสำหรับตัดสินขึ้นมาเช่นเดียวกับในการถดถอยโลจิสติก
สำหรับปัญหา m มิติซึ่งมี w เป็นค่าน้ำหนักในแต่ละมิติ และ b เป็นไบแอส ฟังก์ชันตัดสินคือ
..(1.1)
แต่จะมีข้อกำหนดสำคัญเพิ่มเติมคือ ค่าฟังก์ชันนี้จะมีค่าเป็น -1 ที่ขอบนึง และเป็น 1 ที่อีกขอบ
ค่าของฟังก์ชันตัดสินในสองมิติ f(x) = x1w1+x2w2+b แสดงได้ดังในรูปนี้
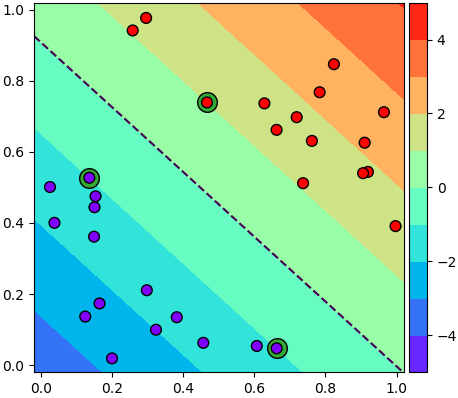
สำหรับจุดเวกเตอร์ค้ำยันที่อยู่ตรงขอบฝั่งบวกจะต้องมีค่าเป็น 1 ส่วนขอบฝั่งลบจะต้องมีค่าเป็น -1 นั่นคือ
..(1.2)
(เงื่อนไขอันนี้เป็นแค่กรณีขอบแข็งเท่านั้น ถ้าขอบนุ่มจะไม่เป็นเช่นนี้ เพราะจะมีบางตัวอยู่ในขอบได้ แต่เพื่อความง่ายตอนนี้จะพิจารณากรณีขอบแข็งก่อน)
ดังนั้นถ้าให้ระยะห่างจากเวกเตอร์ค้ำยันไปยังเส้นแบ่งที่อยู่กึ่งกลางขอบแบ่งเป็น d ตามในรูปนี้
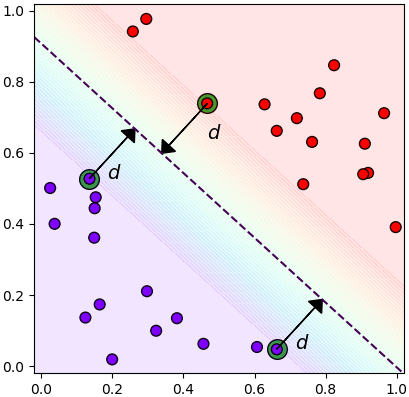
จะได้ว่า
..(1.3)
เป้าหมายของเราคือทำให้ค่า d มากที่สุด นั่นก็หมายถึงทำให้ค่า ||w|| เล็กที่สุด
แต่โดยทั่วไปแล้ว เนื่องจากเหตุผลทางเทคนิค คนมักจะพิจาณาค่า ||w||2/2
..(1.4)
คือถ้า ||w||2/2 เล็กสุด ||w|| ก็ย่อมเล็กสุดด้วย หาอันไหนก็เหมือนกัน แต่เขามองกันว่า ||w||2/2 คำนวณง่ายกว่า
นอกจากนี้ จากการที่กำหนดไว้ว่าให้ไม่มีจุดไหนอยู่ในบริเวณขอบกั้น หมายความว่าค่าของทุกจุดจะต้องอยู่ต่ำกว่า -1 หรือ มากกว่า 1 ดังนั้นอาจเปลี่ยนจากสมการ (1.2) เป็นอสมการแบบนี้
..(1.5)
เมื่อ i เป็นดัชนีของจุดใดๆก็ตาม โดย z คือค่าที่แสดงถึงกลุ่มประเภทข้อมูล z=1 กลุ่มลบ z=-1 ดังนั้นถ้าอยู่กลุ่มบวก ค่า f(x) จะต้องมากกว่า 1 แต่ถ้าอยู่กลุ่มลบต้องน้อยกว่า -1
ให้ระวังว่าค่า z ต่างจากกรณีของการถดถอยโลจิสติก เพราะใน SVM ให้ z เป็น -1,1 แต่ในการถดถอยโลจิสติกจะเป็น 0,1
สรุปโดยรวมแล้วสิ่งที่เรามีตอนนี้คือเป้าหมายที่ว่าจะทำให้ ||w||2/2 มีค่าเล็กที่สุด แล้วก็มีเงื่อนไขตามสมการ (1.5)
โดยทั่วไปแล้ววิธีการที่ใช้สำหรับงานนี้ก็คือ ใช้ตัวคูณลากรองจ์ ร่วมกับเงื่อนไข KKT
ต่อไปจะแนะนำวิธีคำนวณ แต่เนื่องจากเนื้อหาค่อนข้างลึก มีแต่คณิตศาสตร์ สำหรับคนที่ไม่ถนัดหรือไม่ต้องการรู้ลึก ให้ข้ามไปอ่านหัวข้อ "วิธีการเคอร์เนล" เลย
ตัวคูณลากรองจ์
ตัวคูณลากรองจ์ (拉格朗日乘数, Lagrange multipliers) เป็นวิธีการสำหรับหาค่าสูงสุดหรือต่ำสุดของฟังก์ชันอะไรสักอย่างโดยมีเงื่อนไขบางอย่างเป็นตัวกำหนด
ตัวคูณลากรองจ์นี้ยังเป็นหลักการพื้นฐานที่ต่อยอดไปสู่กลศาสตร์แบบลากรองจ์ (拉格朗日力学, Lagrangian mechanics) ซึ่งมักมีสอนในวิชากลศาสตร์ระดับมหาวิทยาลัย
ขออธิบายด้วยการยกตัวอย่าง สมมุติว่าเรามีฟังก์ชันนึงที่ต้องการหาค่าต่ำสุด คือ
..(2.1)
โดยมีเงื่อนไขจำกัดคือ
..(2.2)
แบบนี้สามารถแก้ปัญหาได้โดยนิยามค่าที่เรียกว่าลากรองเจียน (拉格朗日量, Lagrangian)
..(2.3)
โดย a ในที่นี้เรียกว่าเป็นตัวคูณลากรองจ์
เมื่อพิจารณาว่าโดยปกติแล้วที่จุดสูงสุดหรือต่ำสุด ปริพันธ์ย่อยของทุกตัวแปรจะต้องเป็น 0 นั่นคือ
..(2.4)
แบบนี้พอแก้สมการ (2.2) และ (2.4) ออกมาก็จะได้ว่า
..(2.5)
ลองวาดเป็นคอนทัวร์และเส้นกราฟก็จะเห็นชัด ตรงจุดที่มีดาวขาวคือจุดต่ำสุดที่หาออกมาได้ เป็นจุดบนเส้นโค้งที่ค่าบนคอนทัวร์ต่ำสุด
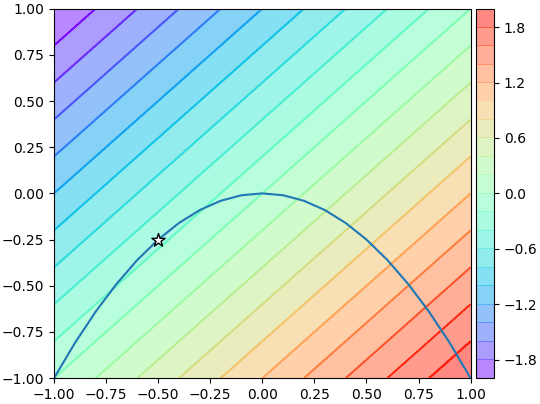
สำหรับกรณีทั่วไปที่ซับซ้อนขึ้นฟังก์ชันเงื่อนไขมีอยู่หลายตัวจะได้ว่า
..(2.6)
เงื่อนไข KKT
ตัวคูณลากรองจ์ใช้หาค่าต่ำสุดให้ฟังก์ชันที่มีอีกสมการมาคอยเป็นเงื่อนไข แต่ว่าสิ่งที่เป็นเงื่อนไขของเป้าหมายการแก้ SVM ของเรานั้นคืออสมการ (1.5) เป็นอสมการ ไม่ใช่สมการ
วิธีการสามารถนำมาใช้กับกรณีได้เช่นกัน เพียงแต่ต้องเพิ่มเงื่อนไขที่เรียกว่าเงื่อนไขของคารุช-คูน-ทักเกอร์ (Karush-Kuhn-Tucker Conditions) หรือเรียกย่อๆว่าเงื่อนไข KKT
ก่อนอื่น จากสมการ (2.6) เมื่อแทนค่า h(x) ด้วยสมการ (1.4) และแทนค่า g(x) โดยใช้อสมการ (1.5) มาทำเป็นสมการ จะได้
..(3.1)
และ
..(3.2)
..(3.3)
โดยจะต้องมีเงื่อนไขเพิ่มเข้ามาคือ
..(3.4)
ซึ่งกรณีหลังคือกรณีของจุดที่เป็นเวกเตอร์ค้ำยัน นั่นหมายความว่าตัวคูณลากรองจ์จะมีค่าเมื่อจุดนั้นเป็นเวกเตอร์ค้ำยันเท่านั้น ดังนั้น
..(3.5)
และเนื่องจาก zi เป็น 1 หรือ -1 ดังนั้น zizi = 1 จึงได้
..(3.6)
โดย S คือเซ็ตของเวกเตอร์ค้ำยัน และ ns คือจำนวนของเวกเตอร์ค้ำยัน
แทนค่าสมการ (3.2) และ (3.6) ลงในสมการ (1.1) จะได้
..(3.7)
จากนั้นแทนสมการ (3.2) และ (3.3) เข้าไปในสมการ (3.1) ได้
..(3.8)
ที่เหลือก็แค่หาค่าตัวคูณลากรองจ์ ai ที่เหมาะสมให้เจอ
วิธีการเคอร์เนล
ก่อนจะไปสู่เรื่องการหาค่าตัวคูณลากรองจ์ มีเรื่องที่จำเป็นต้องพูดถึงเพื่อที่จะทำให้อยู่ในรูปทั่วไปมากขึ้น
จากตัวอย่างที่ผ่านมาตั้งแต่ตอนต้นนั้นเป็นการแบ่งแบบเส้นตรงตลอด นั่นคือฟังก์ชันตัดสิน f(x) เป็นฟังก์ชันเชิงเส้น
SVM นั้นเดิมทีถูกคิดขึ้นมาตั้งแต่ปี 1963 ในตอนนั้นมันถูกใช้แค่เพื่อเป็นตัวแบ่งเชิงเส้น แต่ในปี 1992 มีคนคิดวิธีที่ทำให้ SVM สามารถแบ่งโดยไม่ต้องใช้เส้นตรงได้ ทำให้แก้ปัญหาที่ไม่เป็นเชิงเส้นได้
วิธีการที่จะทำให้ SVM ทำฟังก์ชันตัดสินเป็นอะไรที่ไม่ใช่เชิงเส้นได้นั้นคือการใช้ วิธีการเคอร์เนล (核方法, kernel method) หรือบางทีก็เรียกว่า ลูกเล่นเคอร์เนล (核技巧, kernel trick)
รายละเอียดเกี่ยวกับหลักการพื้นฐานของวิธีการเคอร์เนลได้เขียนไว้ใน https://phyblas.hinaboshi.com/20180724
ภาพตัวอย่างแสดงการแบ่งด้วย SVM แบบไม่เป็นเชิงเส้น เมื่อใช้วิธีการเคอร์เนล
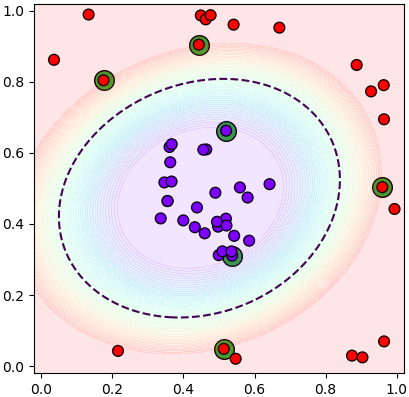
จะเห็นว่ากลุ่มหนึ่งกองอยู่ตรงกลางและอีกกลุ่มอยู่ไกลออกไป โดยมีขอบกั้นวางตัวคั่นเป็นเส้นโค้งอย่างสวยงาม
เคอร์เนลที่ถูกใช้เพื่อทำ SVM ในภาพนี้เรียกว่า เคอร์เนลฟังก์ชันฐานแนวรัศมี (径向基函数核, Radial basis function kernel) นิยมเรียกย่อๆว่า RBF เป็นเคอร์เนลที่นิยมใช้กันมากที่สุด
ลักษณะของฟังก์ชัน RBF คือจะมีจุดศูนย์กลางอยู่จุดนึง ที่จุดนั้นฟังก์ชันนั้นมีค่าสูงสุด และเมื่อไกลออกไปจะมีค่าต่ำลง
ที่จริงแล้วฟังก์ชัน RBF เองก็มีนิยามอยู่หลายแบบ แต่ RBF แบบที่ใช้บ่อยสุดโดยทั่วไปคือฟังก์ชันเกาส์ นิยามดังนี้
..(4.1)
วิธีการเคอร์เนลนั้นเป็นการแปลงระบบพิกัดจากข้อมูลเดิมไปสู่ปริภูมิใหม่แล้วพิจารณาค่าในปริภูมินั้น
เพื่อความเข้าใจลองวาดภาพเพื่อแสดงการแปลงพิกัดจากตำแหน่งใน ๒ มิติไปเป็น ๓ มิติซึ่งเป็นฟังก์ชันเคอร์เนล RBF ของระยะห่างจากจุด (0.2,0.2),(0.8,0.2),(0.5,0.6) พอแปลงเป็นแบบนี้แล้วก็จะถูกแบ่งด้วยระนาบตรงได้ในระบบพิกัดใหม่
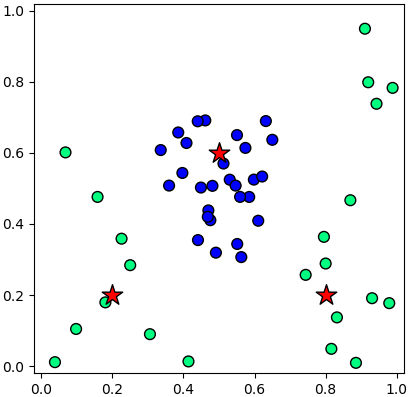
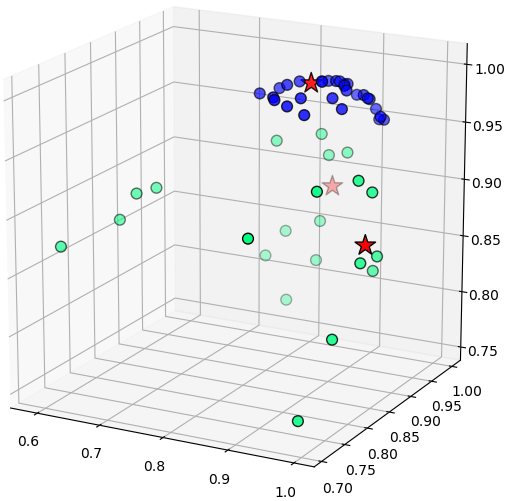
ดังนั้นการที่เห็นว่าเมื่อใช้วิธีการเคอร์เนลแล้วข้อมูลถูกแบ่งด้วยเส้นโค้งได้นั้น จริงๆแล้วมันแบ่งเป็นเส้นตรงอยู่ในระบบพิกัดใหม่
เมื่อใช้วิธีการเคอร์เนล ฟังก์ชันตัดสินก็จะกลายเป็นแบบนี้
..(4.2)
..(4.3)
ส่วนลากรองเจียนจะได้เป็น
..(4.4)
ในกรณีเชิงเส้น เคอร์เนลจะเป็นแบบนี้
..(4.5)
ซึ่งเมื่อแทนลงสมการก็จะกลับไปสู่สมการ (3.6), (3.7) และ (3.8) ดังนั้นถือว่าสมการ (4.2), (4.3) และ (4.4) เป็นรูปทั่วไปปรับขึ้นมาสำหรับใช้กับเคอร์เนล
วิธีการหาค่าตัวคูณลากรองจ์
กลับมาที่การหาค่าตัวคูณลากรองจ์
วิธีการอาจมีอยู่หลายทางด้วยกัน โดยอาจใช้เทคนิคการเคลื่อนลงตามความชัน (梯度下降法, Gradient descent) เช่นเดียวกับการถดถอยโลจิสติก
(รายละเอียดขอให้อ่านจากบทความเรื่องการถดถอยโลจิสติก ไม่กล่าวซ้ำในนี้)
อย่างไรก็ตาม แค่ใช้วิธีการเคลื่อนลงตามความชันธรรมดานั้นยังไม่เพียงพอ ปี 1998 จึงมีคนคิดอัลกอริธึมที่เรียกว่า การปรับปรุงให้ต่ำสุดเป็นลำดับ (序列最小优化算法, Sequential minimal optimization, SMO) เมื่อใช้แล้วทำให้การหาค่าเป็นไปอย่างมีประสิทธิภาพขึ้นมาก
คือปกติถ้าใช้การเคลื่อนลงตามความชัน ก็คือหาอนุพันธ์ย่อยของ L เทียบกับ ai แล้วก็ใช้เป็นค่าความชันสำหรับปรับแก้ค่าต่อไป
จากสมการ (4.4) หาอนุพันธ์ย่อยได้แบบนี้
..(5.1)
แต่จริงๆปัญหานั้นซับซ้อนกว่าที่คิด ไม่เพียงแค่มีตัวแปรที่เกี่ยวข้องเยอะ ยังมีเรื่องของการที่ถูกจำกัดด้วยเงื่อนไข KKT คือ สมการ (3.4) ด้วย ทำให้ไม่สามารถปรับค่า a ได้อย่างอิสระโดยดูแค่เฉพาะความชันจากสมการ (5.1)
หากจะค่อยๆปรับค่า a ไปทีละตัวโดยไม่มีการเปลี่ยนอีกตัวตาม ก็จะเกิดการฝืนกฎนี้ขึ้นทันที ดังนั้นจึงต้องแก้ปัญหาด้วยการปรับค่ามันพร้อมกันทีละ ๒ ตัว
เมื่อลองพิจารณาโดยเพ่งไปที่ ๒ ตัว ลากรองเจียนอาจเขียนใหม่โดยแจกแจงแยกเอาส่วนที่เกี่ยวข้องกับ ๒ ตัวนี้ออกมาเป็น
..(5.2)
โดย a1 และ a2 คือตัวคูณลากรองจ์ของ ๒ ตัวที่พิจารณา ส่วน 久 เป็นค่าส่วนที่ไม่ได้เกี่ยวข้องอะไรกับ a1 และ a2
จากตรงนี้ถ้าแก้สมการต่อไปก็จะยาวจึงขอละไว้ แต่สุดท้ายแล้วผลที่จะได้ก็คือ
..(5.3)
โดยที่
..(5.4)
เพียงแต่มีเงื่อนไขอยู่ตามข้อ (3.4) ว่า
..(5.5)
และค่า a ทั้งหมดต้องไม่ต่ำกว่า 0 และนอกจากนี้ยังมีข้อจำกัดในกรณีที่เป็น SVM แบบขอบนุ่ม คือจะต้องไม่เกินค่าคงที่ C
..(5.6)
กรณีขอบแข็งก็คือค่า C เป็นอนันต์ คือไม่มีข้อจำกัดตรงนี้ แต่พอ C น้อย ai ก็จะถูกจำกัดไม่ให้ขึ้นสูงมากเกินไป
ผลจากข้อจำกัดเหล่านี้จะทำให้เกิดสถานการณ์ที่ต่างกันไปตามความสัมพันธ์ระหว่างค่า z1 และ z2 คือ
กรณีที่ z1=z2
..(5.7)
กรณีที่ z1≠z2
..(5.8)
หลังจากได้ a2 แล้วก็หา a1 ใหม่ได้ โดยจากสมการ (5.5) เมื่อพิจารณาว่า ai ตัวอื่นที่ไม่ใช่ ๒ ตัวแรกไม่มีการเปลี่ยนแปลง ดังนั้นการเปลี่ยนค่าของ a1 ก็ขึ้นกับ a2 จึงได้ว่า
..(5.9)
และเนื่องจาก z1z1 = 1 ดังนั้นได้
..(5.10)
เมื่อได้ค่า a1 และ a2 ใหม่เสร็จแล้วก็กลับไปเลือกจุดต่อไปมาพิจารณาอีก ทำซ้ำไปเรื่อยๆจนกว่าจะสามารถแบ่งได้เรียบร้อย
การเขียน SVM ด้วยไพธอน
เมื่อเข้าใจหลักการแล้ว สุดท้ายก็ได้เวลาเขียนโค้ดสำหรับใช้งานจริงขึ้นมา โดยจะขอเขียนในรูปแบบของคลาส เพื่อความสะดวกในการใช้งาน
หลักการทำงานของโปรแกรมก็คือ
1. กำหนดค่า a ตั้งต้นทุกค่าเป็น 0 ไว้
2. เลือก ๒ จุดมาพิจารณา
3. คำนวนฟังก์ชันตัดสินและเคอร์เนลระหว่างสองจุดนั้น
4. คำนวณค่า a2 ใหม่
5. ตรวจดูเงื่อนไขเพื่อให้ค่า a2 ใหม่อยู่ในขอบเขต
6. คำนวณค่า a1 ใหม่จาก a2 ที่ได้
7. คัดเลือกจุดที่ค่า a/C สูงกว่าค่าที่กำหนดมาเป็นเวกเตอร์ค้ำยัน
8. คำนวณค่า b ใหม่
9. ทำซ้ำตั้งแต่ข้อ 2. ไปเรื่อยๆจนกว่าจะพอใจ
เขียนออกมาเป็นโค้ดได้ตามนี้
โค้ดนี้ถูกเขียนขึ้นมาในแบบที่ง่ายๆและตรงไปตรงมาตามสมการและขั้นตอนที่เขียนไว้ข้างต้น แต่ในความเป็นจริงแล้วประสิทธิภาพยังค่อนข้างต่ำ ความเร็วก็ช้าด้วย
แล้วการเลือก ๒ ตัวที่จะมาพิจารณาในแต่ละรอบนั้นในที่นี้ใช้การสุ่ม แต่จริงๆมีอัลกอริธึมในการเลือกที่ดีที่สุดอยู่
มีวิธีการเขียนที่เพิ่มประสิทธิภาพและเร็วขึ้นมาก แต่ก็มีความซับซ้อนขึ้นอีก เป็นอัลกอริธึมที่ใช้ใน LIBSVM ซึ่งเป็นไลบรารีสำหรับ SVM ในภาษาซี ซึ่งถูกใช้งานจริงอย่างกว้างขวาง
หากลงรายละเอียดก็จะยาวเกินความจำเป็น จึงจะขอลงแค่โค้ดไว้
การใช้งานเหมือนโค้ดอันแรก แต่จะทั้งเร็วและถูกต้องกว่ามาก
จากนั้นลองเอามาใช้ ลองสร้างข้อมูลสองกลุ่มแล้วแบ่งด้วยเคอร์เนลทั้งแบบเชิงเส้นและ RBF ดู
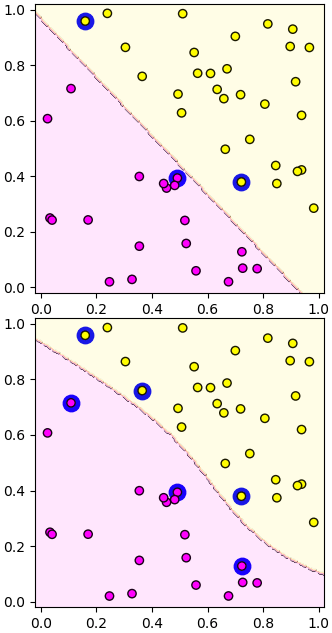
ตำแหน่ง, ค่า a*z และดัชนีของเวกเตอร์ค้ำยันถูกเก็บอยู่ใน .X_sv, .az_sv และ .i_sv สามารถนำมาใช้ได้
เช่นลองพิจารณาข้อมูลที่ไม่สามารถแบ่งเป็นเชิงเส้นได้ และทำการแบ่งด้วยเคอร์เนล RBF จากนั้นลองดูค่าในระบบพิกัดของ RBF ดู
จะเห็นว่าเมื่อแปลงพิกัดด้วยเคอร์เนลแล้วข้อมูลจะถูกแบ่งด้วยเส้นตรงได้ในพิกัดนั้น
สรุปส่งท้าย
จะเห็นได้ว่า SVM เป็นเทคนิคที่ค่อนข้างเข้าใจยาก การจะเขียนโปรแกรม SVM ได้ต้องอาศัยความรู้คณิตศาสตร์ที่ซับซ้อนพอสมควร ดังนั้นตำราส่วนใหญ่มักจะอธิบายแต่หลักการคร่าวๆแล้วแนะนำให้ไปใช้มอดูลที่มีอยู่แล้วเช่น sklearn
โค้ดที่เขียนมาในนี้ทั้งหมดเป็นการเขียนแบบง่ายๆเพื่อความเข้าใจ อย่างไรก็ตาม ทั้งความเร็วและความยืดหยุ่นในการใช้ก็ยังไม่อาจสู้มอดูลที่มีอยู่แล้วเช่น sklearn ดังนั้นสุดท้ายแล้วก็ยังแนะนำให้ใช้ sklearn
ในบทความต่อไปจะเขียนถึงวิธีการใช้ SVM ด้วย sklearn ยังมีรายละเอียดบางอย่างเกี่ยวกับ SVM ที่ยังไม่ได้พูดถึง ก็จะเขียนถึงในนั้นด้วย https://phyblas.hinaboshi.com/20180712
อ้างอิง
ในบทความนี้จะแนะนำตั้งแต่หลักการทำงานพื้นฐานของ SVM และวิธีคำนวณ ไปจนถึงการเขียนโค้ดไพธอนเพื่อสร้างโปรแกรมสำหรับจำแนกประเภทข้อมูลอย่างง่าย
หลักการทั่วไป
SVM เป็นการเรียนรู้ของเครื่องแบบมีผู้สอนซึ่งใช้ในการจำแนกประเภทข้อมูลออกเป็น ๒ กลุ่มโดยการหาเส้นกั้น
หลักการพื้นฐานนี้ใกล้เคียงกับการถดถอยโลจิสติก (逻辑回归, logistic regression)
อย่างไรก็ตาม SVM มีแนวคิดที่ซับซ้อนกว่า หากยังไม่เข้าใจการถดถอยโลจิสติกก็ยากที่จะเข้าใจ SVM ได้ ดังนั้นบทความนี้จะเขียนโดยถือว่าเป็นการต่อยอดจากเนื้อหาเรื่องการถดถอยโลจิสติก
ดังนั้นขอแนะนำให้อ่านบทความนี้ก่อน >> https://phyblas.hinaboshi.com/20161103
ในการถดถอยโลจิสติกนั้นหลักการหาเส้นแบ่งคั่นจะทำโดยการคำนวณค่าเสียหายจากฟังก์ชันซิกมอยด์ และพยายามทำให้ค่าเสียหายนั้นน้อยที่สุด
แต่สำหรับ SVM แล้วสิ่งที่ใช้พิจารณาในการแบ่งก็คือการหาช่องว่างที่จะทำให้ทั้ง ๒ กลุ่มแยกห่างออกจากกันมากที่สุด สร้างช่องว่างระหว่าง ๒ กลุ่มให้มากที่สุด
ช่องว่างที่ว่านี้ถูกเรียกว่าขอบกั้น แสดงด้วยสีรุ้งในภาพนี้ ส่วนเส้นประคือกึ่งกลาง

จะเห็นว่ามีไม่มีจุดไหนเลยอยู่ในบริเวณขอบกั้น แต่จะมีบางจุดที่อยู่ตรงขอบกั้นพอดี ซึ่งแสดงเป็นวงล้อมสีเขียวในภาพนี้
พวกจุดที่ตั้งอยู่บนขอบกั้นนี้จะถูกเรียกว่าเวกเตอร์ค้ำยัน (支持向量, support vector) ซึ่งเป็นที่มาของชื่อวิธีการนั่นเอง จุดเหล่านี้ทำหน้าที่ค้ำยันขอบกั้นที่แบ่งระหว่าง ๒ กลุ่ม
จากในภาพที่เห็นนี้จะเห็นว่ามีเวกเตอร์ค้ำยันอยู่ ๓ จุด แต่จริงๆแล้วในทางปฏิบัติอาจมีกี่จุดก็ได้ ซึ่งจะกล่าวถึงต่อไป
อย่างไรก็ตามในบางกรณีข้อมูลก็มีความคลาดเคลื่อนผิดพลาดจนทำให้มีการซ้อนเกี่ยวปนกันบ้างทำให้ไม่อาจแยกให้มีช่องว่างแบบนี้ได้ เช่นแบบนี้

ดังนั้นโดยทั่วไปแล้วจึงมีการอลุ่มอล่วยให้มีข้อมูลบางส่วนสามารถอยู่ในขอบได้ แบบนี้

กรณีขอบที่มีการอลุ่มอล่วยแบบนี้จะเรียกว่าขอบนุ่ม (软间隔, soft margin) ส่วนแบบที่ไม่ยอมให้มีอะไรอยู่ที่ขอบเลยจะเรียกว่าขอบเข็ง (硬间隔, hard margin)
ขอบนุ่มมักจะหนา และขอบแข็งมักจะบาง หนานุ่มบางแข็ง (กรอบ) เช่นเดียวกับพิซซา ดังนั้นนึกภาพพิซซาตามอาจจะทำให้เห็นภาพง่ายขึ้นได้บ้าง แม้จะไม่เกี่ยวข้องกันโดยตรงก็ตาม
ภาพพิซซาหนานุ่มและบางกรอบ

ลองดูสองภาพนี้ เทียบกันจะเห็นว่าทำขอบนุ่มสักหน่อยดูแล้วแบ่งได้สมเหตุสมผลขึ้นดีกว่าทู่ซี้จะแบ่งแบบขอบแข็ง แม้ว่าจะแบ่งได้ก็ตาม


ดังนั้นการทำขอบนุ่มจึงเป็นการป้อนกันการเรียนรู้เกิน หลักการใกล้เคียงกับการเรกูลาไรซ์ของการถดถอยโลจิสติก ดังที่เขียนไปใน https://phyblas.hinaboshi.com/20170928
และจะเห็นว่าขอบนุ่มมีแนวโน้มจะใช้เวกเตอร์ค้ำยันเยอะกว่า
ขอบนุ่มก็มีระดับความนุ่มอยู่ ซึ่งมักกำหนดด้วยพารามิเตอร์ C ซึ่งจะกล่าวถึงรายละเอียดต่อไปภายหลัง ยิ่ง C มีค่าน้อยขอบก็ยิ่งหนานุ่ม แต่ถ้า C มากจนเป็นอนันต์ก็จะเป็นขอบแข็ง
ขอบจะนุ่มหรือแข็งแค่ไหนถึงจะดีก็แล้วแต่ข้อมูลที่พิจารณา ไม่มีคำตอบตายตัว เหมือนกับพิซซา จะเลือกกินขอบหนานุ่มหรือบางกรอบก็แล้วแต่คน
การหาขอบแบ่ง
เมื่อรู้เป้าหมายว่าต้องหาเส้นแบ่งแล้ว ต่อไปก็คือจะหาเส้นแบ่งอย่างไรดี ว่าหลักการมาฟังดูเหมือนจะง่าย แต่พอคิดจะทำจริงๆแล้วไม่ใช่เรื่องง่ายอย่างที่คิด
SVM นั้นจะมีการสร้างฟังก์ชันเชิงเส้นสำหรับตัดสินขึ้นมาเช่นเดียวกับในการถดถอยโลจิสติก
สำหรับปัญหา m มิติซึ่งมี w เป็นค่าน้ำหนักในแต่ละมิติ และ b เป็นไบแอส ฟังก์ชันตัดสินคือ
..(1.1)
แต่จะมีข้อกำหนดสำคัญเพิ่มเติมคือ ค่าฟังก์ชันนี้จะมีค่าเป็น -1 ที่ขอบนึง และเป็น 1 ที่อีกขอบ
ค่าของฟังก์ชันตัดสินในสองมิติ f(x) = x1w1+x2w2+b แสดงได้ดังในรูปนี้

สำหรับจุดเวกเตอร์ค้ำยันที่อยู่ตรงขอบฝั่งบวกจะต้องมีค่าเป็น 1 ส่วนขอบฝั่งลบจะต้องมีค่าเป็น -1 นั่นคือ
..(1.2)
(เงื่อนไขอันนี้เป็นแค่กรณีขอบแข็งเท่านั้น ถ้าขอบนุ่มจะไม่เป็นเช่นนี้ เพราะจะมีบางตัวอยู่ในขอบได้ แต่เพื่อความง่ายตอนนี้จะพิจารณากรณีขอบแข็งก่อน)
ดังนั้นถ้าให้ระยะห่างจากเวกเตอร์ค้ำยันไปยังเส้นแบ่งที่อยู่กึ่งกลางขอบแบ่งเป็น d ตามในรูปนี้

จะได้ว่า
..(1.3)
เป้าหมายของเราคือทำให้ค่า d มากที่สุด นั่นก็หมายถึงทำให้ค่า ||w|| เล็กที่สุด
แต่โดยทั่วไปแล้ว เนื่องจากเหตุผลทางเทคนิค คนมักจะพิจาณาค่า ||w||2/2
..(1.4)
คือถ้า ||w||2/2 เล็กสุด ||w|| ก็ย่อมเล็กสุดด้วย หาอันไหนก็เหมือนกัน แต่เขามองกันว่า ||w||2/2 คำนวณง่ายกว่า
นอกจากนี้ จากการที่กำหนดไว้ว่าให้ไม่มีจุดไหนอยู่ในบริเวณขอบกั้น หมายความว่าค่าของทุกจุดจะต้องอยู่ต่ำกว่า -1 หรือ มากกว่า 1 ดังนั้นอาจเปลี่ยนจากสมการ (1.2) เป็นอสมการแบบนี้
..(1.5)
เมื่อ i เป็นดัชนีของจุดใดๆก็ตาม โดย z คือค่าที่แสดงถึงกลุ่มประเภทข้อมูล z=1 กลุ่มลบ z=-1 ดังนั้นถ้าอยู่กลุ่มบวก ค่า f(x) จะต้องมากกว่า 1 แต่ถ้าอยู่กลุ่มลบต้องน้อยกว่า -1
ให้ระวังว่าค่า z ต่างจากกรณีของการถดถอยโลจิสติก เพราะใน SVM ให้ z เป็น -1,1 แต่ในการถดถอยโลจิสติกจะเป็น 0,1
สรุปโดยรวมแล้วสิ่งที่เรามีตอนนี้คือเป้าหมายที่ว่าจะทำให้ ||w||2/2 มีค่าเล็กที่สุด แล้วก็มีเงื่อนไขตามสมการ (1.5)
โดยทั่วไปแล้ววิธีการที่ใช้สำหรับงานนี้ก็คือ ใช้ตัวคูณลากรองจ์ ร่วมกับเงื่อนไข KKT
ต่อไปจะแนะนำวิธีคำนวณ แต่เนื่องจากเนื้อหาค่อนข้างลึก มีแต่คณิตศาสตร์ สำหรับคนที่ไม่ถนัดหรือไม่ต้องการรู้ลึก ให้ข้ามไปอ่านหัวข้อ "วิธีการเคอร์เนล" เลย
ตัวคูณลากรองจ์
ตัวคูณลากรองจ์ (拉格朗日乘数, Lagrange multipliers) เป็นวิธีการสำหรับหาค่าสูงสุดหรือต่ำสุดของฟังก์ชันอะไรสักอย่างโดยมีเงื่อนไขบางอย่างเป็นตัวกำหนด
ตัวคูณลากรองจ์นี้ยังเป็นหลักการพื้นฐานที่ต่อยอดไปสู่กลศาสตร์แบบลากรองจ์ (拉格朗日力学, Lagrangian mechanics) ซึ่งมักมีสอนในวิชากลศาสตร์ระดับมหาวิทยาลัย
ขออธิบายด้วยการยกตัวอย่าง สมมุติว่าเรามีฟังก์ชันนึงที่ต้องการหาค่าต่ำสุด คือ
..(2.1)
โดยมีเงื่อนไขจำกัดคือ
..(2.2)
แบบนี้สามารถแก้ปัญหาได้โดยนิยามค่าที่เรียกว่าลากรองเจียน (拉格朗日量, Lagrangian)
..(2.3)
โดย a ในที่นี้เรียกว่าเป็นตัวคูณลากรองจ์
เมื่อพิจารณาว่าโดยปกติแล้วที่จุดสูงสุดหรือต่ำสุด ปริพันธ์ย่อยของทุกตัวแปรจะต้องเป็น 0 นั่นคือ
..(2.4)
แบบนี้พอแก้สมการ (2.2) และ (2.4) ออกมาก็จะได้ว่า
..(2.5)
ลองวาดเป็นคอนทัวร์และเส้นกราฟก็จะเห็นชัด ตรงจุดที่มีดาวขาวคือจุดต่ำสุดที่หาออกมาได้ เป็นจุดบนเส้นโค้งที่ค่าบนคอนทัวร์ต่ำสุด

สำหรับกรณีทั่วไปที่ซับซ้อนขึ้นฟังก์ชันเงื่อนไขมีอยู่หลายตัวจะได้ว่า
..(2.6)
เงื่อนไข KKT
ตัวคูณลากรองจ์ใช้หาค่าต่ำสุดให้ฟังก์ชันที่มีอีกสมการมาคอยเป็นเงื่อนไข แต่ว่าสิ่งที่เป็นเงื่อนไขของเป้าหมายการแก้ SVM ของเรานั้นคืออสมการ (1.5) เป็นอสมการ ไม่ใช่สมการ
วิธีการสามารถนำมาใช้กับกรณีได้เช่นกัน เพียงแต่ต้องเพิ่มเงื่อนไขที่เรียกว่าเงื่อนไขของคารุช-คูน-ทักเกอร์ (Karush-Kuhn-Tucker Conditions) หรือเรียกย่อๆว่าเงื่อนไข KKT
ก่อนอื่น จากสมการ (2.6) เมื่อแทนค่า h(x) ด้วยสมการ (1.4) และแทนค่า g(x) โดยใช้อสมการ (1.5) มาทำเป็นสมการ จะได้
..(3.1)
และ
..(3.2)
..(3.3)
โดยจะต้องมีเงื่อนไขเพิ่มเข้ามาคือ
..(3.4)
ซึ่งกรณีหลังคือกรณีของจุดที่เป็นเวกเตอร์ค้ำยัน นั่นหมายความว่าตัวคูณลากรองจ์จะมีค่าเมื่อจุดนั้นเป็นเวกเตอร์ค้ำยันเท่านั้น ดังนั้น
..(3.5)
และเนื่องจาก zi เป็น 1 หรือ -1 ดังนั้น zizi = 1 จึงได้
..(3.6)
โดย S คือเซ็ตของเวกเตอร์ค้ำยัน และ ns คือจำนวนของเวกเตอร์ค้ำยัน
แทนค่าสมการ (3.2) และ (3.6) ลงในสมการ (1.1) จะได้
..(3.7)
จากนั้นแทนสมการ (3.2) และ (3.3) เข้าไปในสมการ (3.1) ได้
..(3.8)
ที่เหลือก็แค่หาค่าตัวคูณลากรองจ์ ai ที่เหมาะสมให้เจอ
วิธีการเคอร์เนล
ก่อนจะไปสู่เรื่องการหาค่าตัวคูณลากรองจ์ มีเรื่องที่จำเป็นต้องพูดถึงเพื่อที่จะทำให้อยู่ในรูปทั่วไปมากขึ้น
จากตัวอย่างที่ผ่านมาตั้งแต่ตอนต้นนั้นเป็นการแบ่งแบบเส้นตรงตลอด นั่นคือฟังก์ชันตัดสิน f(x) เป็นฟังก์ชันเชิงเส้น
SVM นั้นเดิมทีถูกคิดขึ้นมาตั้งแต่ปี 1963 ในตอนนั้นมันถูกใช้แค่เพื่อเป็นตัวแบ่งเชิงเส้น แต่ในปี 1992 มีคนคิดวิธีที่ทำให้ SVM สามารถแบ่งโดยไม่ต้องใช้เส้นตรงได้ ทำให้แก้ปัญหาที่ไม่เป็นเชิงเส้นได้
วิธีการที่จะทำให้ SVM ทำฟังก์ชันตัดสินเป็นอะไรที่ไม่ใช่เชิงเส้นได้นั้นคือการใช้ วิธีการเคอร์เนล (核方法, kernel method) หรือบางทีก็เรียกว่า ลูกเล่นเคอร์เนล (核技巧, kernel trick)
รายละเอียดเกี่ยวกับหลักการพื้นฐานของวิธีการเคอร์เนลได้เขียนไว้ใน https://phyblas.hinaboshi.com/20180724
ภาพตัวอย่างแสดงการแบ่งด้วย SVM แบบไม่เป็นเชิงเส้น เมื่อใช้วิธีการเคอร์เนล

จะเห็นว่ากลุ่มหนึ่งกองอยู่ตรงกลางและอีกกลุ่มอยู่ไกลออกไป โดยมีขอบกั้นวางตัวคั่นเป็นเส้นโค้งอย่างสวยงาม
เคอร์เนลที่ถูกใช้เพื่อทำ SVM ในภาพนี้เรียกว่า เคอร์เนลฟังก์ชันฐานแนวรัศมี (径向基函数核, Radial basis function kernel) นิยมเรียกย่อๆว่า RBF เป็นเคอร์เนลที่นิยมใช้กันมากที่สุด
ลักษณะของฟังก์ชัน RBF คือจะมีจุดศูนย์กลางอยู่จุดนึง ที่จุดนั้นฟังก์ชันนั้นมีค่าสูงสุด และเมื่อไกลออกไปจะมีค่าต่ำลง
ที่จริงแล้วฟังก์ชัน RBF เองก็มีนิยามอยู่หลายแบบ แต่ RBF แบบที่ใช้บ่อยสุดโดยทั่วไปคือฟังก์ชันเกาส์ นิยามดังนี้
..(4.1)
วิธีการเคอร์เนลนั้นเป็นการแปลงระบบพิกัดจากข้อมูลเดิมไปสู่ปริภูมิใหม่แล้วพิจารณาค่าในปริภูมินั้น
เพื่อความเข้าใจลองวาดภาพเพื่อแสดงการแปลงพิกัดจากตำแหน่งใน ๒ มิติไปเป็น ๓ มิติซึ่งเป็นฟังก์ชันเคอร์เนล RBF ของระยะห่างจากจุด (0.2,0.2),(0.8,0.2),(0.5,0.6) พอแปลงเป็นแบบนี้แล้วก็จะถูกแบ่งด้วยระนาบตรงได้ในระบบพิกัดใหม่
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def kernel(x1,x2,gamma=0.5):
return np.exp(-gamma*((x1-x2)**2).sum(-1))
X = np.random.uniform(0,1,[50,2])
z = 6*(X[:,0]-0.5)**2-X[:,1]>0
X[z==0] = 0.5+(X[z==0]-0.5)*0.5
K = np.array([[0.2,0.2],[0.8,0.2],[0.5,0.6]])
X_ = np.array([kernel(X,np.array(K[i])) for i in [0,1,2]]).T
K_ = np.array([kernel(K,np.array(K[i])) for i in [0,1,2]]).T
plt.axes(aspect=1,xlim=[-0.02,1.02],ylim=[-0.02,1.02])
plt.scatter(X[:,0],X[:,1],s=60,c=z,edgecolor='k',cmap='winter')
plt.scatter(K[:,0],K[:,1],s=240,c='r',marker='*',edgecolor='k')
ax = plt.figure(figsize=[6,6]).add_axes([0,0,1,1],projection='3d')
ax.scatter(X_[:,0],X_[:,1],X_[:,2],s=60,c=z,edgecolor='k',cmap='winter')
ax.scatter(K_[:,0],K_[:,1],K_[:,2],s=240,c='r',marker='*',edgecolor='k')
plt.show()

ดังนั้นการที่เห็นว่าเมื่อใช้วิธีการเคอร์เนลแล้วข้อมูลถูกแบ่งด้วยเส้นโค้งได้นั้น จริงๆแล้วมันแบ่งเป็นเส้นตรงอยู่ในระบบพิกัดใหม่
เมื่อใช้วิธีการเคอร์เนล ฟังก์ชันตัดสินก็จะกลายเป็นแบบนี้
..(4.2)
..(4.3)
ส่วนลากรองเจียนจะได้เป็น
..(4.4)
ในกรณีเชิงเส้น เคอร์เนลจะเป็นแบบนี้
..(4.5)
ซึ่งเมื่อแทนลงสมการก็จะกลับไปสู่สมการ (3.6), (3.7) และ (3.8) ดังนั้นถือว่าสมการ (4.2), (4.3) และ (4.4) เป็นรูปทั่วไปปรับขึ้นมาสำหรับใช้กับเคอร์เนล
วิธีการหาค่าตัวคูณลากรองจ์
กลับมาที่การหาค่าตัวคูณลากรองจ์
วิธีการอาจมีอยู่หลายทางด้วยกัน โดยอาจใช้เทคนิคการเคลื่อนลงตามความชัน (梯度下降法, Gradient descent) เช่นเดียวกับการถดถอยโลจิสติก
(รายละเอียดขอให้อ่านจากบทความเรื่องการถดถอยโลจิสติก ไม่กล่าวซ้ำในนี้)
อย่างไรก็ตาม แค่ใช้วิธีการเคลื่อนลงตามความชันธรรมดานั้นยังไม่เพียงพอ ปี 1998 จึงมีคนคิดอัลกอริธึมที่เรียกว่า การปรับปรุงให้ต่ำสุดเป็นลำดับ (序列最小优化算法, Sequential minimal optimization, SMO) เมื่อใช้แล้วทำให้การหาค่าเป็นไปอย่างมีประสิทธิภาพขึ้นมาก
คือปกติถ้าใช้การเคลื่อนลงตามความชัน ก็คือหาอนุพันธ์ย่อยของ L เทียบกับ ai แล้วก็ใช้เป็นค่าความชันสำหรับปรับแก้ค่าต่อไป
จากสมการ (4.4) หาอนุพันธ์ย่อยได้แบบนี้
..(5.1)
แต่จริงๆปัญหานั้นซับซ้อนกว่าที่คิด ไม่เพียงแค่มีตัวแปรที่เกี่ยวข้องเยอะ ยังมีเรื่องของการที่ถูกจำกัดด้วยเงื่อนไข KKT คือ สมการ (3.4) ด้วย ทำให้ไม่สามารถปรับค่า a ได้อย่างอิสระโดยดูแค่เฉพาะความชันจากสมการ (5.1)
หากจะค่อยๆปรับค่า a ไปทีละตัวโดยไม่มีการเปลี่ยนอีกตัวตาม ก็จะเกิดการฝืนกฎนี้ขึ้นทันที ดังนั้นจึงต้องแก้ปัญหาด้วยการปรับค่ามันพร้อมกันทีละ ๒ ตัว
เมื่อลองพิจารณาโดยเพ่งไปที่ ๒ ตัว ลากรองเจียนอาจเขียนใหม่โดยแจกแจงแยกเอาส่วนที่เกี่ยวข้องกับ ๒ ตัวนี้ออกมาเป็น
..(5.2)
โดย a1 และ a2 คือตัวคูณลากรองจ์ของ ๒ ตัวที่พิจารณา ส่วน 久 เป็นค่าส่วนที่ไม่ได้เกี่ยวข้องอะไรกับ a1 และ a2
จากตรงนี้ถ้าแก้สมการต่อไปก็จะยาวจึงขอละไว้ แต่สุดท้ายแล้วผลที่จะได้ก็คือ
..(5.3)
โดยที่
..(5.4)
เพียงแต่มีเงื่อนไขอยู่ตามข้อ (3.4) ว่า
..(5.5)
และค่า a ทั้งหมดต้องไม่ต่ำกว่า 0 และนอกจากนี้ยังมีข้อจำกัดในกรณีที่เป็น SVM แบบขอบนุ่ม คือจะต้องไม่เกินค่าคงที่ C
..(5.6)
กรณีขอบแข็งก็คือค่า C เป็นอนันต์ คือไม่มีข้อจำกัดตรงนี้ แต่พอ C น้อย ai ก็จะถูกจำกัดไม่ให้ขึ้นสูงมากเกินไป
ผลจากข้อจำกัดเหล่านี้จะทำให้เกิดสถานการณ์ที่ต่างกันไปตามความสัมพันธ์ระหว่างค่า z1 และ z2 คือ
กรณีที่ z1=z2
..(5.7)
กรณีที่ z1≠z2
..(5.8)
หลังจากได้ a2 แล้วก็หา a1 ใหม่ได้ โดยจากสมการ (5.5) เมื่อพิจารณาว่า ai ตัวอื่นที่ไม่ใช่ ๒ ตัวแรกไม่มีการเปลี่ยนแปลง ดังนั้นการเปลี่ยนค่าของ a1 ก็ขึ้นกับ a2 จึงได้ว่า
..(5.9)
และเนื่องจาก z1z1 = 1 ดังนั้นได้
..(5.10)
เมื่อได้ค่า a1 และ a2 ใหม่เสร็จแล้วก็กลับไปเลือกจุดต่อไปมาพิจารณาอีก ทำซ้ำไปเรื่อยๆจนกว่าจะสามารถแบ่งได้เรียบร้อย
การเขียน SVM ด้วยไพธอน
เมื่อเข้าใจหลักการแล้ว สุดท้ายก็ได้เวลาเขียนโค้ดสำหรับใช้งานจริงขึ้นมา โดยจะขอเขียนในรูปแบบของคลาส เพื่อความสะดวกในการใช้งาน
หลักการทำงานของโปรแกรมก็คือ
1. กำหนดค่า a ตั้งต้นทุกค่าเป็น 0 ไว้
2. เลือก ๒ จุดมาพิจารณา
3. คำนวนฟังก์ชันตัดสินและเคอร์เนลระหว่างสองจุดนั้น
4. คำนวณค่า a2 ใหม่
5. ตรวจดูเงื่อนไขเพื่อให้ค่า a2 ใหม่อยู่ในขอบเขต
6. คำนวณค่า a1 ใหม่จาก a2 ที่ได้
7. คัดเลือกจุดที่ค่า a/C สูงกว่าค่าที่กำหนดมาเป็นเวกเตอร์ค้ำยัน
8. คำนวณค่า b ใหม่
9. ทำซ้ำตั้งแต่ข้อ 2. ไปเรื่อยๆจนกว่าจะพอใจ
เขียนออกมาเป็นโค้ดได้ตามนี้
import numpy as np
import matplotlib.pyplot as plt
# ฟังก์ชันเคอร์เนลเชิงเส้น
def kernel_choengsen(x1,x2):
return (x1*x2).sum(-1)
# สร้างฟังก์ชันเคอร์เนล RBF
def sang_kernel_rbf(gamma):
def kernel_rbf(x1,x2):
return np.exp(-gamma*((x1-x2)**2).sum(-1))
return kernel_rbf
class SVM:
def __init__(self,kernel,C=1):
self.kernel = kernel # ฟังก์ชันที่จะใช้เป็นเคอร์เนล
self.C = C
def rianru(self,X,z,thamsam=10000,a_tamsut=1e-8):
'''
thamsam: จำนวนครั้งที่ทำซ้ำเพื่อเปลี่ยนแก้ค่า
a_tamsut: ค่า a/C ต่ำสุดสำหรับการเป็นเวกเตอร์ค้ำยัน
'''
z = np.where(z>0,1,-1) # กรณีที่ค่าที่ป้อนเข้ามาเป็น 0,1 ให้แก้เป็น -1,1 ก่อน
n = len(z) # จำนวนข้อมูล
a = np.zeros(n) # ค่าตัวคูณลากรองจ์ตั้งต้น
self.b = 0 # b ตั้งต้น
self.i_sv = np.array([]) # เวกเตอร์ค้ำยัน เริ่มแรกว่างเปล่า
for khrangthi in range(thamsam):
i1,i2 = np.random.permutation(n)[:2] # สุ่มเลือกมาสองจุด
a1,a2 = a[i1],a[i2]
X1,X2 = X[i1],X[i2]
z1,z2 = z[i1],z[i2]
f1,f2 = self.f(X1),self.f(X2)
E1,E2 = f1-z1,f2-z2
K11,K12,K22 = self.kernel(X1,X1),self.kernel(X1,X2),self.kernel(X2,X2)
kkk = K11+K22-2*K12
kkk = max(kkk,10e-8) # กันกรณีที่ค่าน้อยเกิน
a2_mai = a2+z2*(E1-E2)/kkk
a2_mai = max(a2_mai,0.)
a2_mai = min(a2_mai,self.C)
if(z1==z2): # กรณี z1 เท่ากับ z2
a2_mai = max(a2_mai,a2+a1-self.C)
a2_mai = min(a2_mai,a2+a1)
else: # กรณี z1 ไม่เท่ากับ z2
a2_mai = max(a2_mai,a2-a1)
a2_mai = min(a2_mai,a2-a1+self.C)
a1_mai = a1 + z1*z2*(a2-a2_mai)
a[i1],a[i2] = a1_mai,a2_mai
# คัดและเก็บเวกเตอร์ค้ำยัน
self.i_sv = np.arange(n)[a>a_tamsut*self.C]
self.X_sv = X[self.i_sv]
self.az_sv = a[self.i_sv]*z[self.i_sv] # ค่า a*z
# คำนวณ b ใหม่
self.b = np.sum([1-(self.az_sv*self.kernel(X[i],self.X_sv)).sum() for i in self.i_sv])
if(self.b):
self.b /= len(self.i_sv)
# ฟังก์ชันตัดสิน
def f(self,X):
if(len(self.i_sv)==0): return 0 # ถ้ายังไม่มีเวกเตอร์ค้ำยัน ให้เป็น 0 ไป
return np.sum(self.kernel(X,self.X_sv)*self.az_sv,-1) + self.b
# จำแนกประเภท [0,1] จาก X
def thamnai(self,X):
return (self.f(X)>=0).astype(int)โค้ดนี้ถูกเขียนขึ้นมาในแบบที่ง่ายๆและตรงไปตรงมาตามสมการและขั้นตอนที่เขียนไว้ข้างต้น แต่ในความเป็นจริงแล้วประสิทธิภาพยังค่อนข้างต่ำ ความเร็วก็ช้าด้วย
แล้วการเลือก ๒ ตัวที่จะมาพิจารณาในแต่ละรอบนั้นในที่นี้ใช้การสุ่ม แต่จริงๆมีอัลกอริธึมในการเลือกที่ดีที่สุดอยู่
มีวิธีการเขียนที่เพิ่มประสิทธิภาพและเร็วขึ้นมาก แต่ก็มีความซับซ้อนขึ้นอีก เป็นอัลกอริธึมที่ใช้ใน LIBSVM ซึ่งเป็นไลบรารีสำหรับ SVM ในภาษาซี ซึ่งถูกใช้งานจริงอย่างกว้างขวาง
หากลงรายละเอียดก็จะยาวเกินความจำเป็น จึงจะขอลงแค่โค้ดไว้
class SVM:
def __init__(self,kernel,C=1):
self.C = C
self.kernel = kernel
def rianru(self,X,z,thamsam,a_tamsut=1e-5,lekpho=1e-3):
'''
thamsam: จำนวนครั้งสูงสุดที่ทำซ้ำเพื่อเปลี่ยนแก้ค่า
a_tamsut: ค่า a/C ต่ำสุดสำหรับการเป็นเวกเตอร์ค้ำยัน
lekpho: ค่าที่เล็กพอที่จะทำให้หยุดโดยไม่ต้องทำซ้ำจนครบ
'''
z = np.where(z,1,-1)
kx = {} # ดิกเก็บค่าเคอร์เนลที่เคยคำนวณแล้วเพื่อประหยัดเวลาคำนวณซ้ำ
n = len(z)
a = np.zeros(n)
ii1 = z>0
ii2 = z<0
khwamchan = -np.ones(n) # ค่าความชันตั้งต้น
for khrangthi in range(thamsam):
# เลือกดัชนีของจุดข้อมูลที่จะใช้พิจารณา
da = -z*khwamchan
ii1_ = np.arange(n)[ii1]
ii2_ = np.arange(n)[ii2]
i1 = ii1_[np.argmax(da[ii1_])]
i2 = ii2_[np.argmin(da[ii2_])]
# เงื่อนไขการหยุด ถ้าความชันของทั้งสองต่างกันน้อยพอก็หยุด
m1 = -z[i1]*khwamchan[i1]
m2 = -z[i2]*khwamchan[i2]
if(m1-m2 <= lekpho):
break
# คำนวณเคอร์เนล หรือดึงข้อมูลถ้ามีอยู่แล้ว
if(i1 in kx):
kxi = kx[i1]
else:
kxi = self.kernel(X,X[i1])*z*z[i1]
kx[i1] = kxi
if(i2 in kx):
kxj = kx[i2]
else:
kxj = self.kernel(X,X[i2])*z*z[i2]
kx[i2] = kxj
kxii,kxjj,kxij = kxi[i1],kxj[i2],kxi[i2]
zz = z[i1]*z[i2]
if(zz==1):
d_max = min(self.C-a[i1],a[i2])
d_min = max(-a[i1],a[i2]-self.C)
else:
d_max = min(self.C-a[i1],self.C-a[i2])
d_min = max(-a[i1],-a[i2])
kkk = kxii + kxjj - 2*zz*kxij
kkk = max(kkk,10e-8)
d = -(khwamchan[i1]-khwamchan[i2]*zz)/kkk
d = max(min(d,d_max),d_min)
# ปรับค่า a
a[i1] += d
a[i2] += -d*zz
# ปรับค่าความชัน
khwamchan += d*kxi - d*zz*kxj
# ปรับรายการดัชนีของสองกลุ่ม
for i in [i1,i2]:
if(z[i]>0 and a[i]/self.C<=1-a_tamsut):
ii1[i] = 1
elif(z[i]<0 and a_tamsut<=a[i]/self.C):
ii1[i] = 1
else:
ii1[i] = 0
if(z[i]>0 and a_tamsut<=a[i]/self.C):
ii2[i] = 1
elif(z[i]<0 and a[i]/self.C<=1-a_tamsut):
ii2[i] = 1
else:
ii2[i] = 0
# คัดและเก็บเวกเตอร์ค้ำยัน
self.i_sv = np.arange(n)[a>a_tamsut*self.C]
self.X_sv = X[self.i_sv]
self.az_sv = a[self.i_sv]*z[self.i_sv]
self.b = (m1+m2)/2.
self.thamsampai = khrangthi+1 # บันทึกว่าทำซ้ำไปกี่ครั้ง
def f(self,X):
return np.sum(self.kernel(X,self.X_sv)*self.az_sv,-1) + self.b
def thamnai(self,X):
return self.f(X)>=0การใช้งานเหมือนโค้ดอันแรก แต่จะทั้งเร็วและถูกต้องกว่ามาก
จากนั้นลองเอามาใช้ ลองสร้างข้อมูลสองกลุ่มแล้วแบ่งด้วยเคอร์เนลทั้งแบบเชิงเส้นและ RBF ดู
X = np.random.uniform(0,0.9,[50,2])
z = np.where(X[:,0]+X[:,1]>0.9,1,0)
X[z==1] += 0.1
thamsam = 1000
C = 1e5
gamma = 5
mx,my = np.meshgrid(np.linspace(-0.02,1.02,200),np.linspace(-0.02,1.02,200))
mX = np.stack([mx.ravel(),my.ravel()],1)
kernel_rbf = sang_kernel_rbf(gamma)
kernel = [kernel_choengsen,kernel_rbf]
plt.figure(figsize=[4,8])
for k in [0,1]:
svm = SVM(kernel[k],C)
svm.rianru(X,z,thamsam)
mz = np.reshape(([svm.thamnai(mX[i]) for i in range(len(mX))]),[200,-1])
plt.subplot(211+k,aspect=1,xlim=[-0.02,1.02],ylim=[-0.02,1.02])
plt.scatter(svm.X_sv[:,0],svm.X_sv[:,1],s=140,c='b')
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='spring')
plt.contour(mx,my,mz,cmap='gray',zorder=1,linestyles='--')
plt.contourf(mx,my,mz,alpha=0.1,cmap='spring')
plt.tight_layout()
plt.show()
ตำแหน่ง, ค่า a*z และดัชนีของเวกเตอร์ค้ำยันถูกเก็บอยู่ใน .X_sv, .az_sv และ .i_sv สามารถนำมาใช้ได้
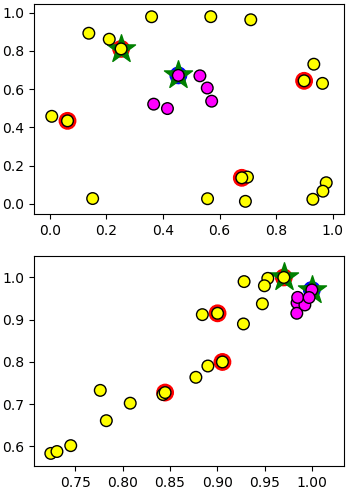
เช่นลองพิจารณาข้อมูลที่ไม่สามารถแบ่งเป็นเชิงเส้นได้ และทำการแบ่งด้วยเคอร์เนล RBF จากนั้นลองดูค่าในระบบพิกัดของ RBF ดู
X = np.random.uniform(0,1,[25,2])
z = ((X[:,0]-0.5)**2+(X[:,1]-0.5)**2)>0.15
X[z==0] = 0.5+(X[z==0]-0.5)*0.5
kernel = sang_kernel_rbf(0.5)
svm = SVM(kernel,C=1e5)
svm.rianru(X,z,1000)
imm = np.array([svm.az_sv.argmin(),svm.az_sv.argmax()]) # ดัชนีเวกเตอร์ค้ำยันที่ค่า a มากสุดฝั่งลบและฝั่งบวก
Xk = kernel(X,svm.X_sv[imm[0]]),svm.kernel(X,svm.X_sv[imm[1]]) # แปลงพิกัดด้วยเคอร์เนล
Xk = np.stack(Xk,1) # ตำแหน่งในระบบพิกัดใหม่
plt.figure(figsize=[4,6])
plt.subplot(211) # แสดงตำแหน่งในระบบพิกัดเดิม
plt.scatter(svm.X_sv[:,0],svm.X_sv[:,1],s=140,c=z[svm.i_sv],cmap='bwr') # เวกเตอร์ค้ำยันทั้งหมด กรองน้ำเงินและแดง
plt.scatter(svm.X_sv[imm,0],svm.X_sv[imm,1],marker='*',s=450,c='g') # เวกเตอร์ค้ำยัน ๒ ตัวที่พิจารณา ใช้ดาวเขียว
plt.scatter(X[:,0],X[:,1],s=70,c=z,edgecolor='k',cmap='spring')
plt.subplot(212) # แสดงตำแหน่งในระบบพิกัดใหม่
plt.scatter(Xk[svm.i_sv,0],Xk[svm.i_sv,1],s=140,c=z[svm.i_sv],cmap='bwr')
plt.scatter(Xk[svm.i_sv[imm],0],Xk[svm.i_sv[imm],1],marker='*',s=450,c='g')
plt.scatter(Xk[:,0],Xk[:,1],s=70,c=z,edgecolor='k',cmap='spring')
plt.show()
print(svm.az_sv)
จะเห็นว่าเมื่อแปลงพิกัดด้วยเคอร์เนลแล้วข้อมูลจะถูกแบ่งด้วยเส้นตรงได้ในพิกัดนั้น
สรุปส่งท้าย
จะเห็นได้ว่า SVM เป็นเทคนิคที่ค่อนข้างเข้าใจยาก การจะเขียนโปรแกรม SVM ได้ต้องอาศัยความรู้คณิตศาสตร์ที่ซับซ้อนพอสมควร ดังนั้นตำราส่วนใหญ่มักจะอธิบายแต่หลักการคร่าวๆแล้วแนะนำให้ไปใช้มอดูลที่มีอยู่แล้วเช่น sklearn
โค้ดที่เขียนมาในนี้ทั้งหมดเป็นการเขียนแบบง่ายๆเพื่อความเข้าใจ อย่างไรก็ตาม ทั้งความเร็วและความยืดหยุ่นในการใช้ก็ยังไม่อาจสู้มอดูลที่มีอยู่แล้วเช่น sklearn ดังนั้นสุดท้ายแล้วก็ยังแนะนำให้ใช้ sklearn
ในบทความต่อไปจะเขียนถึงวิธีการใช้ SVM ด้วย sklearn ยังมีรายละเอียดบางอย่างเกี่ยวกับ SVM ที่ยังไม่ได้พูดถึง ก็จะเขียนถึงในนั้นด้วย https://phyblas.hinaboshi.com/20180712
อ้างอิง
https://www.amazon.co.jp/Python機械学習プログラミング-達人データサイエンティストによる理論と実践-impress-top-gearシリーズ-ebook/dp/B01HGIPIAK
https://qiita.com/rennnosuke/items/cd01aa855196340167df
https://qiita.com/rennnosuke/items/fab837825b64bf50be56
https://qiita.com/ta-ka/items/e6fd0b6fc46dbab4a651
https://qiita.com/shuhei_f/items/5c4ff6ed278eb1747a6f
https://qiita.com/pesuchin/items/c55f40b69aa1aec2bd19
http://d.hatena.ne.jp/xyz600/20121202/1354441674
http://aidiary.hatenablog.com/entry/20100502/1272804952
https://ja.wikipedia.org/wiki/サポートベクターマシン
https://ja.wikipedia.org/wiki/ラグランジュの未定乗数法
https://ja.wikipedia.org/wiki/カルーシュ・クーン・タッカー条件
https://ja.wikipedia.org/wiki/逐次最小問題最適化法
https://xacecask2.gitbooks.io/scikit-learn-user-guide-chinese-version/content/sec1.4.html
https://medium.com/@chih.sheng.huang821/機器學習-支撐向量機-support-vector-machine-svm-詳細推導-c320098a3d2e
https://medium.com/@chih.sheng.huang821/機器學習-支撐向量機-support-vector-machine-svm-詳細推導-c320098a3d2e
https://zhuanlan.zhihu.com/p/28660098
https://zhuanlan.zhihu.com/p/28954032
https://zhuanlan.zhihu.com/p/29212107
https://www.cnblogs.com/bentuwuying/p/6444516.html
https://blog.csdn.net/u011067360/article/details/26503719
https://qiita.com/rennnosuke/items/cd01aa855196340167df
https://qiita.com/rennnosuke/items/fab837825b64bf50be56
https://qiita.com/ta-ka/items/e6fd0b6fc46dbab4a651
https://qiita.com/shuhei_f/items/5c4ff6ed278eb1747a6f
https://qiita.com/pesuchin/items/c55f40b69aa1aec2bd19
http://d.hatena.ne.jp/xyz600/20121202/1354441674
http://aidiary.hatenablog.com/entry/20100502/1272804952
https://ja.wikipedia.org/wiki/サポートベクターマシン
https://ja.wikipedia.org/wiki/ラグランジュの未定乗数法
https://ja.wikipedia.org/wiki/カルーシュ・クーン・タッカー条件
https://ja.wikipedia.org/wiki/逐次最小問題最適化法
https://xacecask2.gitbooks.io/scikit-learn-user-guide-chinese-version/content/sec1.4.html
https://medium.com/@chih.sheng.huang821/機器學習-支撐向量機-support-vector-machine-svm-詳細推導-c320098a3d2e
https://medium.com/@chih.sheng.huang821/機器學習-支撐向量機-support-vector-machine-svm-詳細推導-c320098a3d2e
https://zhuanlan.zhihu.com/p/28660098
https://zhuanlan.zhihu.com/p/28954032
https://zhuanlan.zhihu.com/p/29212107
https://www.cnblogs.com/bentuwuying/p/6444516.html
https://blog.csdn.net/u011067360/article/details/26503719
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib