ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๒๑: การแจกแจงอเนกนามและการแจกแจงแบบหมวดหมู่

เขียนเมื่อ 2020/09/11 16:05

แก้ไขล่าสุด 2023/08/26 13:15

ㄍ๏ สารบัญ ๏ㄟ

๛ การแจกแจงความน่าจะเป็นของผลลัพธ์แบบต่างๆ
๛ ค่าคาดหมายและความแปรปรวนของการแจกแจงอเนกนาม
๛ ความสัมพันธ์ระหว่างการแจกแจงอเนกนามกับการแจกแจงทวินามและแบร์นุลลี
๛ การแจกแจงแบบหมวดหมู่
๛ ตัวอย่างกรณีสามหมวดหมู่
๛ ตัวอย่างกรณีมากกว่าสามหมวดหมู่
๛ ความสัมพันธ์กับการแจกแจงชนิดต่างๆ

ต่อจาก บทที่ ๒๐

ในบทนี้จะเป็นเรื่องของการแจกแจงอเนกนามและการแจกแจงแบบหมวดหมู่

การแจกแจงความน่าจะเป็นของผลลัพธ์แบบต่างๆ介

ในบทที่ ๕ ได้เขียนถึงการแจกแจงทวินามไปแล้ว

การแจกแจงแบบทวินามนั้นเป็นการแจกแจงของผลลัพธ์ที่มีแค่ 2 แบบ ซึ่งมักจะหมายถึงสำเร็จกับล้มเหลว

แต่ว่าบ่อยครั้งที่ผลลัพธ์ไม่ได้มีอยู่แค่ 2 แบบ แต่มีหลายแบบกว่านั้น ในกรณีแบบนี้การแจกแจงจะซับซ้อนกว่าเดิมไปอีกขั้น กลายเป็นการแจกแจงที่เรียกว่าการแจกแจงอเนกนาม (多项分布, multinomial distribution)

"ทวิ" แปลว่า "สอง" ส่วน "อเนก" แปลว่า "หลายๆ" ฉะนั้นการแจกแจงแบบอเนกนามก็เป็นการขยายผลจากการแจกแจงทวินามซึ่งมีอยู่แค่ 2 มาเป็นหลายๆ

อาจเทียบได้กับความสัมพันธ์ระหว่างการแจกแจงแบบปกติตัวแปรเดียวกับการแจกแจงแบบปกติหลายตัวแปร

ในที่นี้จะขอเรียกรูปแบบของผลลัพธ์ต่างๆว่า "หมวดหมู่" (类别, category)

ถ้ามีหมวดหมู่ทั้งหมด m หมวดหมู่ ให้

$\vec{k}$ เป็นจำนวนผลลัพธ์ที่ได้ในแต่ละหมวดหมู่

$\begin{align} \vec{k} = \begin{bmatrix} k_1 \\ k_2 \\ \vdots \\ k_m \end{bmatrix} \end{align}$

ความน่าจะเป็นร่วมที่จำนวนครั้งที่ออกจะได้เป็น

$k_1,k_2,...,k_m$ จะเป็นการแจกแจงแบบอเนกนาม คือ

$\begin{align} P(\vec{k}) = P(k_1,k_2,...,k_m) &= n!\prod_{i=1}^m\frac{p_i^{k_i}}{k_i!} \\ &= n! \frac{p_1^{k_1}p_2^{k_2}\cdots p_m^{k_m}}{k_1!k_2! \cdots k_m!} \end{align}$

พารามิเตอร์มี 2 ตัว คือ

$\vec{p}=\begin{bmatrix} p_1 \\ p_2 \\ \vdots \\ p_m \end{bmatrix}$ : ความน่าจะเป็นของแต่ละหมวดหมู่
n: จำนวนครั้งที่ทำการทดลองทั้งหมด

จำนวนรวมทั้งหมดต้องเท่ากับ n พอดี

$\begin{align} \sum_{i=1}^m k_i = n \end{align}$

และความน่าจะเป็นทั้งหมดต้องรวมกันได้เท่ากับ 1 พอดี

$\begin{align} \sum_{i=1}^m p_i = 1 \end{align}$

และเมื่อเป็นค่าความน่าจะเป็นก็แน่นอนว่าต้องอยู่ระหว่าง 0 ถึง 1

$\begin{align} 0≤p_i≤1 \end{align}$

ยกตัวอย่างเช่นทอยลูกเต๋าซึ่งมี 6 หน้าทั้งหมด 100 ครั้ง แล้วนับจำนวนที่ออกแต่ละหน้า ผลลัพธ์ก็จะมี 6 หมวดหมู่ นั่นคือ m=6 ในที่นี้ความน่าจะเป็นแต่ละตัวคือ p₁,p₂,...p₆=1/6 จำนวนครั้งที่ทดลองคือ n=100 จำนวนที่ออกในแต่ละหน้าอาจเขียนแทนด้วย k₁,k₂,...,k₆ เป็นต้น

ลองเขียนเป็นโค้ดสุ่มดูจริงๆในไพธอน

import random,math

m = 6 # จำนวนหน้าลูกเต๋า
n = 100 # จำนวนที่โยน
# สุ่มผลโยน n ครั้ง
x = []
for i in range(n):
    x += [random.randint(1,m)]
# นับจำนวนที่ออกแต่ละหน้า
for i in range(1,m+1):
    ki = x.count(i)
    print(f'k{i} = {ki}')

ผลที่ได้

k1 = 14
k2 = 23
k3 = 15
k4 = 14
k5 = 15
k6 = 19

โดยเฉลี่ยแล้วแต่ละหน้าน่าจะได้สัก 16-17 ครั้ง แต่การทดลองงวดนี้ 2 ดูจะออกมาเยอะเป็นพิเศษ ซึ่งก็เป็นเรื่องที่มีโอกาสเกิดขึ้นได้

ค่าคาดหมายและความแปรปรวนของการแจกแจงอเนกนาม介

ค่าคาดหมายของแต่ละหมวดหมู่คำนวณได้เป็น

$\begin{align} E(k_i) = np_i \end{align}$

ความแปรปรวนของแต่ละหมวดหมู่เป็น

$\begin{align} σ^2_{k_i)} = np_i(1-p_i) \end{align}$

ความแปรปรวนร่วมเกี่ยวระหว่างต่างหมวดหมู่เป็น

$\begin{align} σ_{k_i,k_j}^2 = -np_ip_j \end{align}$

เมื่อ i≠j

และจะได้เมทริกซ์ความแปรปรวนร่วมเกี่ยวเป็น

$\begin{align} Σ = n\begin{bmatrix} p_1(1-p_1) & -p_1p_2 & \cdots & -p_1p_m \\ -p_2p_1 & p_2(1-p_2) & \cdots & -p_2p_m \\ \vdots & \vdots & \ddots & \vdots \\ -p_mp_1 & -p_mp_2 & \cdots & p_m(1-p_m) \end{bmatrix} \end{align}$

ความสัมพันธ์ระหว่างการแจกแจงอเนกนามกับการแจกแจงทวินามและแบร์นุลลี介

ถ้าหาก m=2 ซึ่งก็หมายถึงว่ามีแค่ 2 หมวดหมู่แล้ว การแจกแจงความน่าจะเป็นก็จะได้เป็น

$\begin{align} P(\vec{k}) &= n!\frac{p_1^{k_1}}{k_1!}\frac{p_2^{k_2}}{k_2!} \\ \end{align}$

ความน่าจะเป็นรวมต้องเป็น 1 และผลรวมของ k ต้องเป็น n ดังนั้น

$\begin{align} p_1+p_2 &= 1 \\ p_2 &= 1-p_1 \\ k_1+k_2 &= n \\ k_2 &= n-k_1 \end{align}$

จึงเขียนใหม่ได้เป็น

$\begin{align} P(k_1) &= \frac{n!p_1^{k_1}(1-p_1)^{n-k_1}}{k_1!(n-k_1)!} \\ &= C(n,k_1)p_1^{k_1}(1-p_1)^{n-k_1} \end{align}$

ซึ่งก็จะกลายเป็นการแจกแจงทวินาม (แค่เอาเลข 1 ที่ห้อยอยู่ออกไป)

และถ้า m=2 อีกทั้งยัง n=1 ก็จะกลายเป็นการแจกแจงแบร์นุลลี

$\begin{align} P(k_1) = p_1^{k_1}(1-p_1)^{1-k_1} \end{align}$

ดังนั้นการแจกแจงทวินามก็ถือได้ว่าเป็นกรณีเฉพาะแบบหนึ่งของการแจกแจงอเนกนาม ในกรณีที่หมวดหมู่มีเพียง 2

การแจกแจงแบบหมวดหมู่介

การแจกแจงอเนกนามในกรณีที่ n=1 จะเป็นกรณีเฉพาะที่เรียกว่าการแจกแจงแบบหมวดหมู่ (类别分布, categorical distribution)

$\begin{align} P(\vec{k}) = P(k_1,k_2,...,k_m) = \prod_{i=1}^m\frac{p_i^{k_i}}{k_i!} \end{align}$

ความสัมพันธ์ของการแจกแจงแบบหมวดหมู่กับการแจกแจงอเนกนามนั้นคือเช่นเดียวกับความสัมพันธ์ระหว่างการแจกแจงแบร์นุลลีและการแจกแจงทวินาม

อาจถือได้ว่าทั้งการแจกแจงแบร์นุลลี, การแจกแจงทวินาม, การแจกแจงแบบหมวดหมู่ ล้วนเป็นกรณีพิเศษของการแจกแจงอเนกนาม

$\begin{align} \end{align}$

ตัวอย่างกรณีสามหมวดหมู่介

ลองดูตัวอย่างกรณีที่ง่ายรองลงมาจากกรณี 2 หมวดหมู่ (ซึ่งก็คือการแจกแจงทวินาม) นั่นคือกรณีที่ผลลัพธ์มี 3 หมวดหมู่

ถ้ามี 3 หมวดหมู่ ผลลัพธ์คือจำนวนครั้งที่ได้ในแต่ละหมู่ก็จะมี 3 ค่า เป็น

$\vec{k}=[k_1,k_2,k_3]^T$

เพียงแต่ว่าถ้าทำการทดลอง n ครั้ง จำนวนรวมทั้งหมดก็ย่อมเป็น n แบบนั้นบอกแค่ค่า 2 ตัวแรกก็ย่อมรู้ค่าตัวที่ 3 แน่ชัดอยู่แล้ว

$\begin{align} k_3 = n-k_1-k_2 \end{align}$

ดังนั้นในที่นี้จะแสดงการแจกแจง 2 มิติ ระหว่าง k₁ กับ k₂

ตัวอย่างเช่นให้จำนวนครั้งที่ลองเป็น n=10 แล้วให้

$\vec{p}=[0.5,0.2,0.3]^T$ ผลการแจกแจงจะออกมาแบบนี้

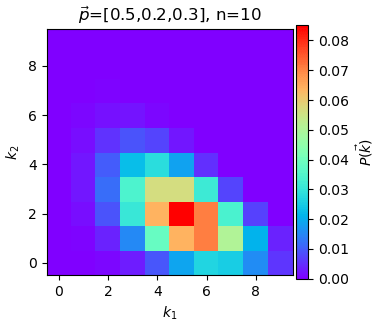
จะเห็นว่าค่าสูงสุดอยู่ที่ k₁=5,k₂=2 (ซึ่งแน่นอนว่า k₃ ก็จะเป็น 3) ซึ่งเป็นจำนวนที่ตรงตามสัดส่วนความน่าจะเป็น และค่าอื่นก็จะมีความน่าจะเป็นน้อยลงลดหลั่นไป

ลองทำเป็นภาพเคลื่อนไหว แสดงกรณีที่ให้

$\vec{p}=[0.3,0.2,0.5]^T$ แล้วเพิ่มจำนวน n ไปเรื่อยๆ

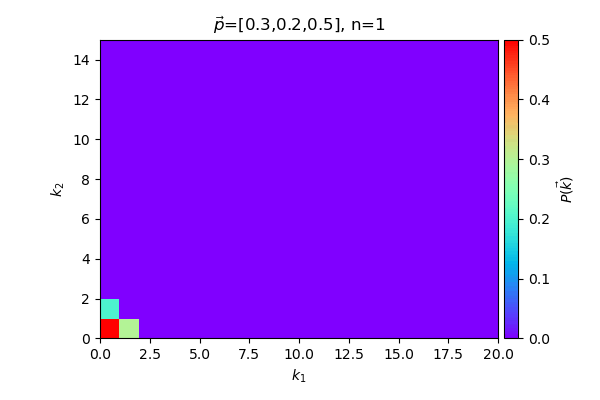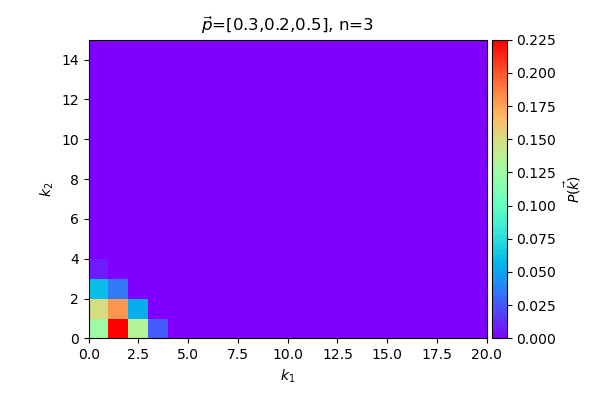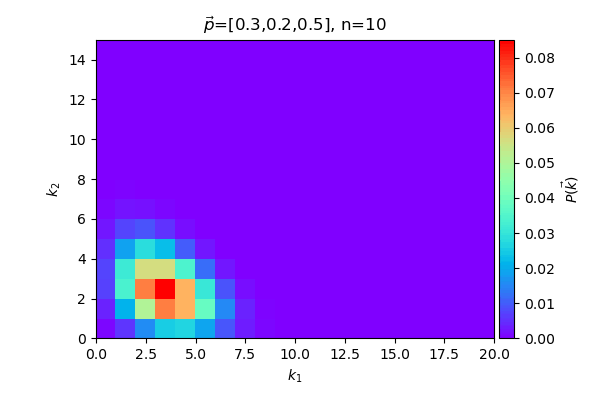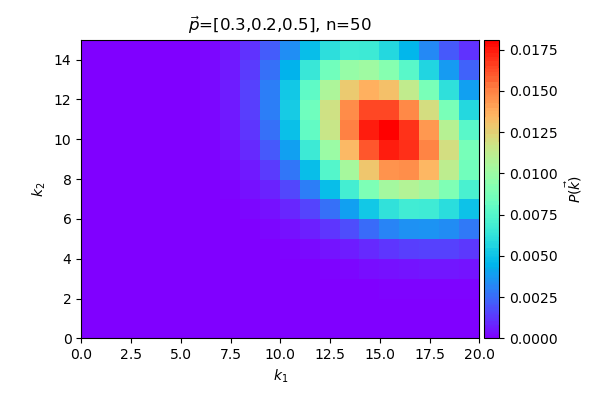
หรือลองดูกรณีที่ให้ n คงที่ที่ 50 แล้วเปลี่ยนค่า

$\vec{p}$ ไปเรื่อยๆ

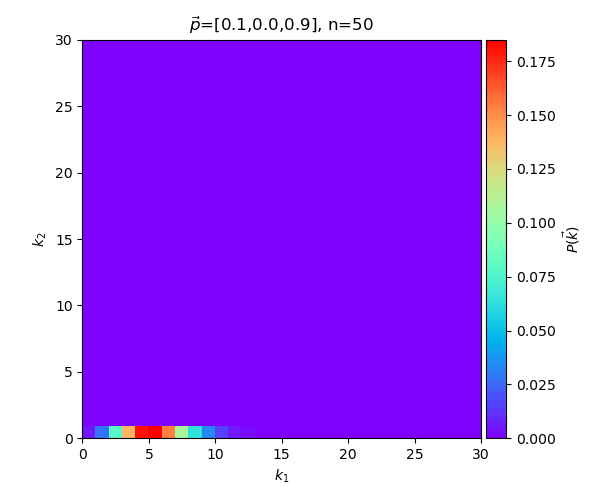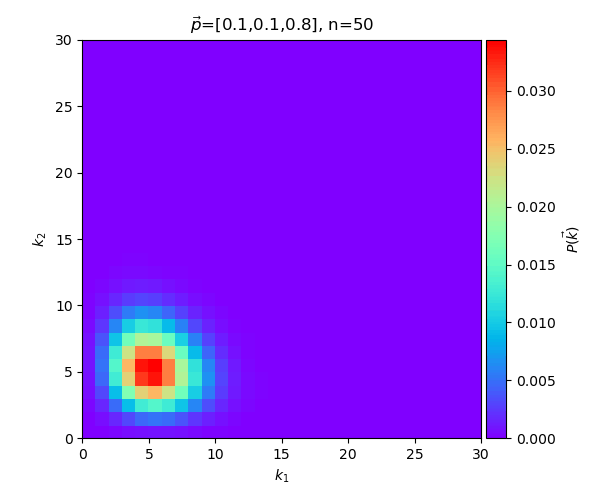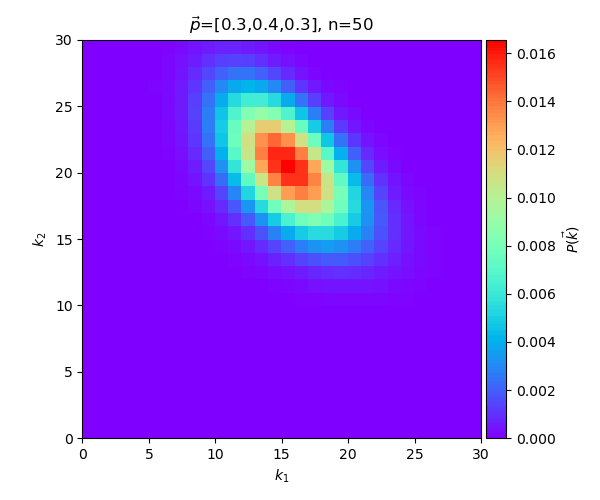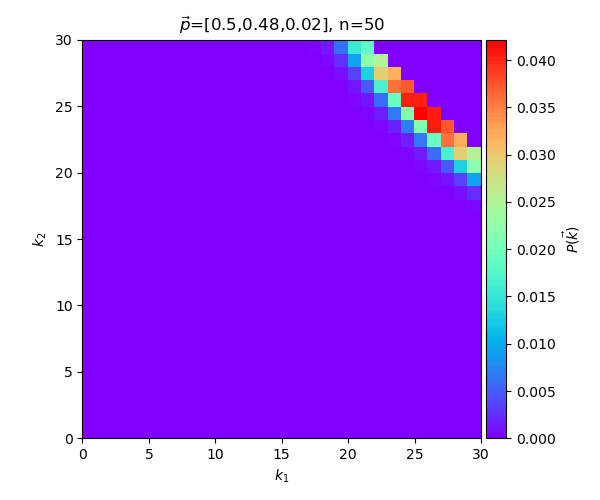
ตัวอย่างกรณีมากกว่าสามหมวดหมู่介

ต่อไปลองมาดูกรณีที่เพิ่มมาอีกหมวด เป็น 4 หมวด ดูการแจกแจงของ k₁,k₂ เหมือนเดิม แต่ให้ k₃ เปลี่ยนไปเรื่อยๆ โดยคงจำนวนค่า n (ส่วน k₄ ก็เป็น n-k₁-k₂-k₃ ไปโดยปริยาย) เทียบดูผลลัพธ์แต่ละกรณี

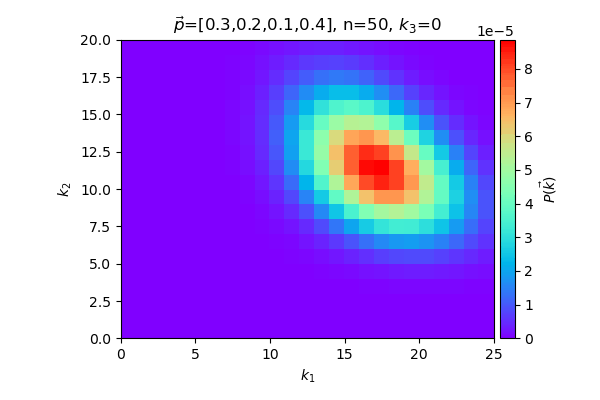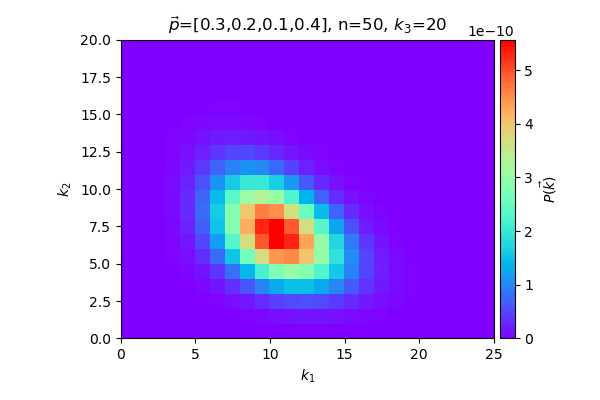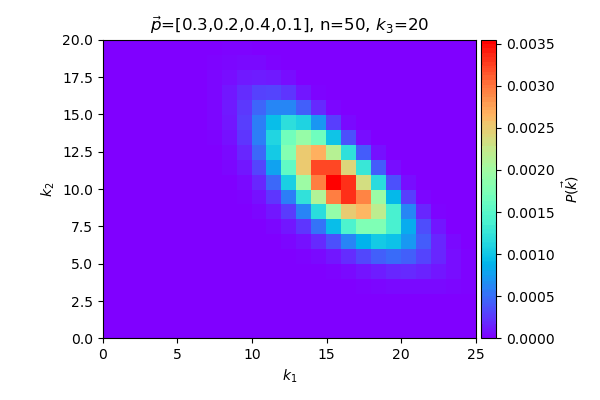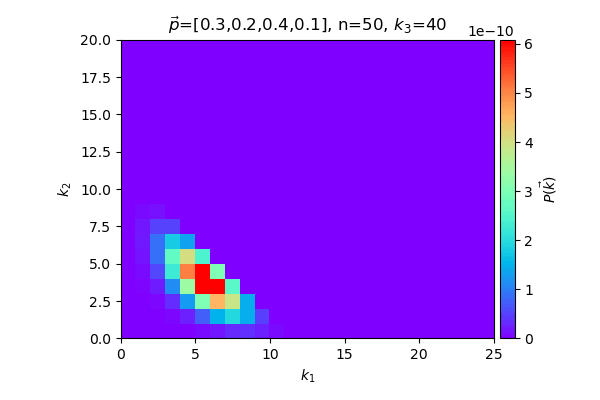
ในที่นี้พยายามแสดงตัวอย่างการแจกแจงเป็นภาพ ซึ่งก็มักจะแสดงได้แค่สองมิติ หรือใช้การเปลี่ยนแปลงตามเวลาเพื่อช่วยเป็นอีกมิติ แต่พอจำนวนหมวดหมู่เพิ่มขึ้นก็มีตัวแปรมากยิ่งขึ้นจึงยากที่จะเขียนแสดงเป็นภาพ แต่โดยรวมแล้วถ้าเข้าใจความหมายก็น่าจะนึกภาพตามออกได้

ผลลัพธ์อาจจะมีมากมาย แต่ถ้ามีรูปแบบแน่นอน จำนวนหมวดหมู่ก็เป็นจำนวนเต็ม แล้วก็ยังใช้การแจกแจงอเนกนามอธิบายการแจกแจงความน่าจะเป็นได้

ความสัมพันธ์กับการแจกแจงชนิดต่างๆ介

สุดท้ายลองมาดูสรุปความสัมพันธ์ระหว่างการแจกแจงต่างๆที่เกี่ยวข้องกัน

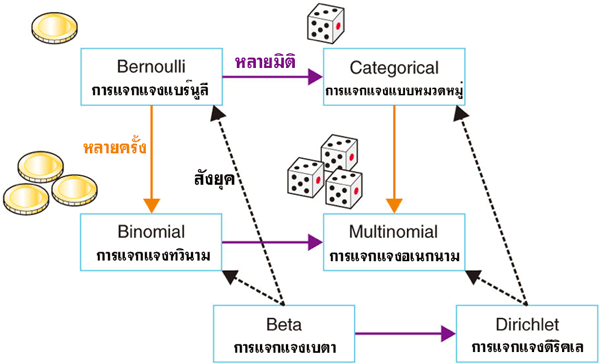
เริ่มจากการแจกแจงแบบแบร์นุลลีซึ่งเป็นการทดลองที่ง่ายที่สุด คือมีผลลัพธ์แค่ 2 แบบคือสำเร็จกับล้มเหลว และทำแค่ 1 ครั้ง

ถ้าเปลี่ยนเป็นทำหลายครั้งก็จะกลายเป็นการแจกแจงทวินาม

ถ้าผลลัพธ์มีหลายแบบ แต่ยังทำแค่ 1 ครั้งก็จะเป็นการแจกแจงแบบหมวดหมู่

ถ้าผลลัพธ์มีหลายแบบ และทำหลายๆครั้งก็จะเป็นการแจกแจงอเนกนาม

ส่วนการแจกแจงเบตาคือความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงทวินามและการแจกแจงแบร์นุลลี

และในทำนองเดียวกัน การแจกแจงดีริคเลคือความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงอเนกนามและการแจกแจงแบบหมวดหมู่

สำหรับเรื่องของการแจกแจงดีริคเลจะเขียนถึงในบทต่อไป

บทถัดไป >> บทที่ ๒๒

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

ดูสถิติของหน้านี้

หมวดหมู่

-- คณิตศาสตร์ >> ความน่าจะเป็น
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python

ไม่อนุญาตให้นำเนื้อหาของบทความไปลงที่อื่นโดยไม่ได้ขออนุญาตโดยเด็ดขาด หากต้องการนำบางส่วนไปลงสามารถทำได้โดยต้องไม่ใช่การก๊อปแปะแต่ให้เปลี่ยนคำพูดเป็นของตัวเอง หรือไม่ก็เขียนในลักษณะการยกข้อความอ้างอิง และไม่ว่ากรณีไหนก็ตาม ต้องให้เครดิตพร้อมใส่ลิงก์ของทุกบทความที่มีการใช้เนื้อหาเสมอ

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

1月	2月	3月	4月
5月	6月	7月	8月
9月	10月	11月	12月

-----------------------------------------

囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧

หมวดหมู่

~ 自我介绍 ~

目录

按类别分日志

查看日志

最近

推荐日志

各月日志

2025年

2024年

2023年

2022年

2021年

找更早以前的日志

ไทย

日本語

中文