manim บทที่ ๒๐: การวาดเส้นกราฟและแผนภูมิแท่ง
เขียนเมื่อ 2021/03/13 12:28
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๑๙
หลังจากที่บทที่แล้วได้พูดถึงการวางระบบพิกัดลงบนภาพแล้ว ในบทนี้จะพูดถึงการวาดเส้นกราฟและแผนภูมิแท่งลงไป
การวาดเส้นกราฟ
ออบเจ็กต์ของแกนกราฟที่สร้างจากคลาส Axes มีเมธอด .get_graph() เอาไว้ใช้วาดกราฟของฟังก์ชันที่ต้องการ
ตัวอย่าง
import manimlib as mnm
import numpy as np
import math
class Manimala(mnm.Scene):
def construct(self):
axes = mnm.Axes(x_range=(-10,14,2),
y_range=(-7,7,2),
axis_config={'stroke_width':5,
'stroke_color':'#c7e5ab'})
axes.add_coordinate_labels()
sengraph = axes.get_graph(lambda x: 0.0025*x**3-1,
x_range=(-11,15,0.1),
color='#abe0e5',
stroke_width=15)
self.add(axes)
self.play(
mnm.Write(sengraph),
run_time=1
)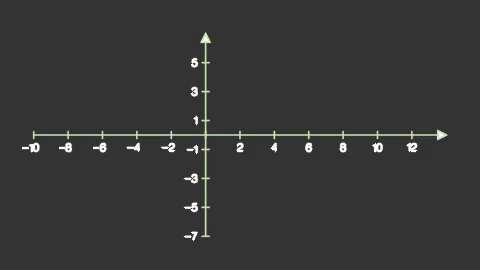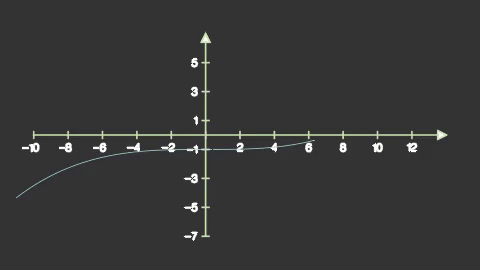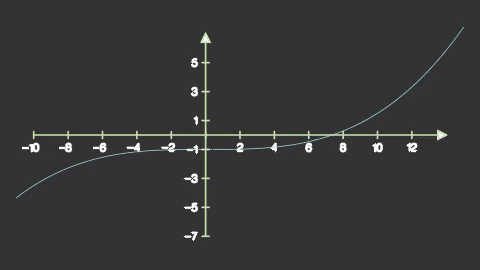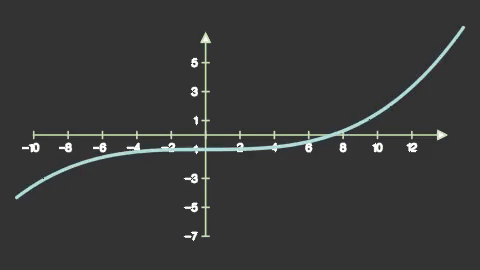
ในที่นี้ x_range ใส่เป็น (x ต่ำสุด, x สูงสุด, ระยะห่างแต่ละจุด)
เมธอด .get_graph_label() เอาไว้เขียนข้อความลงบนกราฟที่วาด
ตัวอย่าง
import manimlib as mnm
class Manimala(mnm.Scene):
def construct(self):
axes = mnm.Axes(x_range=(-12,16,2),
y_range=(-9,8,2),
axis_config={'stroke_width':4,
'stroke_color':'#e5c3ab'})
axes.add_coordinate_labels()
sengraph = axes.get_graph(lambda x: 0.004*x**3-0.05*x**2+4,
x_range=(-11,15,0.1),
color='#bce5ab',
stroke_width=12)
label = axes.get_graph_label(sengraph,r'\frac{x^3}{250}-\frac{x^2}{20}+4')
self.add(axes,label)
self.play(
mnm.Write(sengraph),
run_time=1
)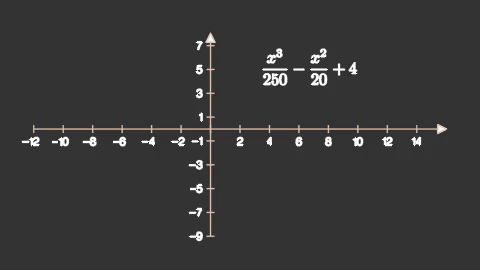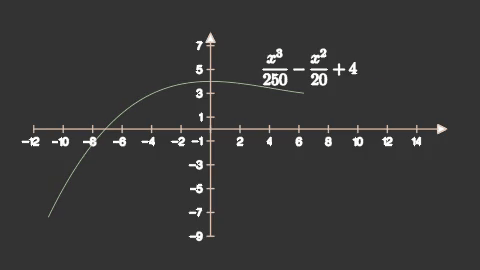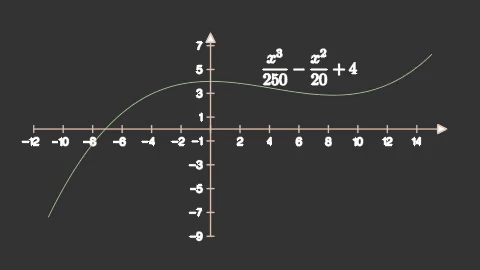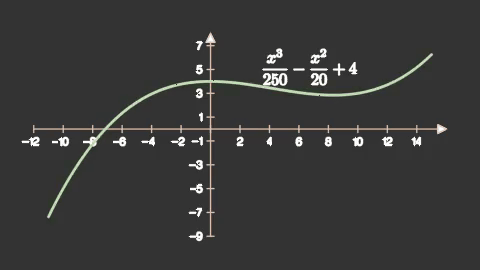
FunctionGraph
คลาส FunctionGraph เอาไว้สร้างกราฟของฟังก์ชันที่ต้องการลงบนพิกัดของตำแหน่งภายในภาพ
ตัวอย่าง
import manimlib as mnm
import numpy as np
class Manimala(mnm.Scene):
def construct(self):
axes = mnm.NumberPlane() # ใส่กราฟพิกัดตำแหน่งในภาพ
axes.add_coordinate_labels()
# วาดกราฟในระบบพิกัดตำแหน่งในภาพขึ้นมา ๓ เส้น
sengraph = mnm.VGroup(mnm.FunctionGraph(np.sin),
mnm.FunctionGraph(lambda x:np.cos(x)*2+x/2,
stroke_width=10,
color='#99bbdd'),
mnm.FunctionGraph(lambda x:np.exp(x)/6-x/2-3))
self.add(axes)
self.play(
mnm.Write(sengraph),
run_time=1,
lag_ratio=0.5
)
ParametricCurve
คลาส ParametricCurve ใช้วาดกราฟที่มีค่าพิกัดเป็น x(t),y(t),z(t) โดย t เป็นตัวแปรหนึ่งที่ไล่ค่าในช่วงของเขตที่กำหนด (กำหนดของเขตที่คีย์เวิร์ด t_range)
ฟังก์ชันที่จะใช้กับ ParametricCurve คือฟังก์ชันที่รับตัวแปร t มาแล้วคืนค่าเป็นอาเรย์ของค่า [x,y,z] (ในที่นี้แสดง ๒ มิติจะใช้แค่ x,y)
ตัวอย่าง
import manimlib as mnm
import numpy as np
class Manimala(mnm.Scene):
def construct(self):
axes = mnm.NumberPlane()
axes.add_coordinate_labels()
def f1(t):
return np.array([2*np.sin(t*12)-4.75,3*np.cos(t*5),0])
def f2(t):
return np.array([2*np.cos(t*7),3.25*np.cos(t*12),0])
def f3(t):
return np.array([2*np.sin(t*13)+4.75,3.5*np.sin(t*9),0])
def f4(t):
return np.array([6*np.cos(t),2.5*np.sin(t),0])
t_range = [0,np.pi*2,np.pi/100]
sengraph = mnm.VGroup(mnm.ParametricCurve(f1,t_range,color='#ff6666'),
mnm.ParametricCurve(f2,t_range,color='#66ff66'),
mnm.ParametricCurve(f3,t_range,color='#6666ff'),
mnm.ParametricCurve(f4,t_range))
self.add(axes)
self.play(
mnm.Write(sengraph),
run_time=1,
lag_ratio=0.2
)
BarChart
คลาส BarChart ใช้วาดแผนภูมิแท่ง
ตัวอย่างการใช้
import manimlib as mnm
import numpy as np
class Manimala(mnm.Scene):
def construct(self):
axes = mnm.BarChart(np.linspace(0.1,2,14)**0.5,
width=12,
height=6,
n_ticks=7,
max_value=1.4,
bar_colors=['#99ff99','#c093d5'],
bar_fill_opacity=0.6,
bar_stroke_width=5,
bar_names='abcdefghijklmn')
self.add(axes)
# วาดแผนภูมิแท่ง
self.play(
mnm.Write(axes),
run_time=1
)
# ปรับค่าแต่ละแท่งภายหลัง
self.play(
axes.animate.change_bar_values(np.zeros(14)),
run_time=1
)