numpy & matplotlib เบื้องต้น บทที่ ๓๔: อาเรย์ของจำนวนเชิงซ้อน
เขียนเมื่อ 2016/06/12 16:38
แก้ไขล่าสุด 2022/07/21 20:37
จำนวนเชิงซ้อน เป็นชนิดข้อมูลชนิดหนึ่งในภาษาไพธอน และมีลักษณะพิเศษที่มากกว่าจำนวนจริง จึงน่านำมากล่าวถึงแยกต่างหากเป็นพิเศษสักหน่อย
numpy มีคำสั่งต่างๆที่ช่วยในการจัดการกับจำนวนเชิงซ้อนภายในอาเรย์ทำให้การใช้งานทำได้สะดวก ซึ่งจะมาพูดถึงกันตรงนี้
สำหรับการจัดการกับจำนวนเชิงซ้อนในเบื้องต้นของภาษาไพธอนที่ไม่เกี่ยวกับ numpy อ่านได้ที่ https://phyblas.hinaboshi.com/20160608
การสร้างอาเรย์ของจำนวนเชิงซ้อน
ตอนที่ประกาศสร้างอาเรย์ขึ้นมาจากลิสต์หากมีสมาชิกเป็นจำนวนเชิงซ้อนแม้แต่ตัว เดียวก็จะได้ชนิดของอาเรย์เป็นจำนวนเชิงซ้อน สมาชิกตัวอื่นทั้งหมดก็จะเขียนอยู่ในรูปจำนวนเชิงซ้อนด้วย
complex128 ในที่นี้เป็นชนิดข้อมูลจำนวนเชิงซ้อนมาตรฐานเมื่อสร้างจำนวนเชิงซ้อนขึ้นมา แล้วไม่กำหนดอะไรเพิ่มเติมก็จะได้ชนิดนี้ นอกจากนี้ยังมี complex64 กับ complex256 ด้วย สามารถกำหนดได้ตอนสร้าง
หรือหากสมาชิกเป็นจำนวนจริงแต่ระบุชนิดเป็นจำนวนเชิงซ้อนก็จะได้อาเรย์ของจำนวนเชิงซ้อนเช่นกัน
หากระบุว่า complex เฉยๆจะได้ชนิด complex128 แต่ถ้าต้องการชนิด 'complex64' หรือ 'complex256' ก็ต้องระบุไปเป็นสายอักขระ
อาเรย์ของจำนวนจริงหากนำมาบวกกับจำนวนเชิงซ้อนก็จะเปลี่ยนได้ผลเป็น จำนวนเชิงซ้อนทันที จะใช้วิธีนี้ในการสร้างอาเรย์จำนวนเชิงซ้อนก็ได้
เมื่ออาเรย์จำนวนจริงคูณกับจำนวนเชิงซ้อน ก็จะได้อาเรย์จำนวนเชิงซ้อนมา
ดังนั้นอาจสร้างอาเรย์ของจำนวนเชิงซ้อนได้โดยการสร้างส่วนจริงและส่วนจินตภาพแยกกันแล้วนำมาบวกกันได้
ต้องระวังว่าอาเรย์ของจำนวนจริงต่อให้นำมาคำนวณยังไงก็ไม่อาจได้จำนวนเชิงซ้อน เช่นต่อให้รู้ว่าจำนวนติดลบยกกำลังแล้วควรจะได้จำนวนเชิงซ้อนก็ตาม
ลักษณะแบบนี้ไม่ว่าจะทำในไพธอน 3 หรือ 2 ก็ให้ผลแบบเดียวกัน
ดังนั้นจึงมีความจำเป็นต้องเปลี่ยนให้อยู่ในรูปเชิงซ้อนก่อน
ส่วนจริง, ส่วนจินตภาพ และสังยุค
ในการหาค่าส่วนจริงและส่วนจินตภาพของจำนวนเชิงซ้อนในอาเรย์อาจใช้ฟังก์ชัน np.real และ np.imag หรืออาจจะดูค่าเป็นแอตทริบิวต์ real และ imag ก็ได้เช่นกัน
ส่วนค่าสังยุคหาได้จาก ฟังก์ชัน np.conj หรืออาจใช้เมธอด conj ก็ได้ (เป็นเมธอด ไม่ใช่แอตทริบิวต์ ต้องมีวงเล็บด้วย)
จำนวนเชิงซ้อนในรูปพิกัดเชิงขั้ว
จำนวนเชิงซ้อนอาจเขียนในรูปแบบเชิงขั้ว แสดงโดยค่าสัมบูรณ์ r และมุมเฟส θ ดังนี้

ค่าสัมบูรณ์หาได้โดยใช้ฟังก์ชัน np.abs หรือ np.absolute (ความจริงแล้วคือฟังก์ชันเดียวกัน np.abs เป็นแค่ชื่อย่อของ np.absolute)
และมุมเฟสหาได้จากฟังก์ชัน np.angle
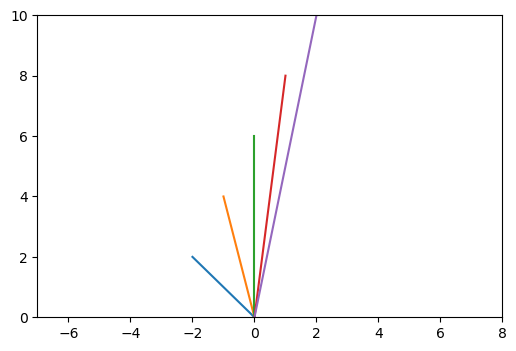
ลองนำมาวาดกราฟของแต่ละจุดโดยให้เส้นลากจากจุด 0 โดยให้แกนนอนเป็นส่วนจริงและแกนตั้งเป็นส่วนจินตภาพ
ลองเขียนในรูปพิกัดเชิงขั้วโดยใช้ค่าสัมบูรณ์และมุมเฟส
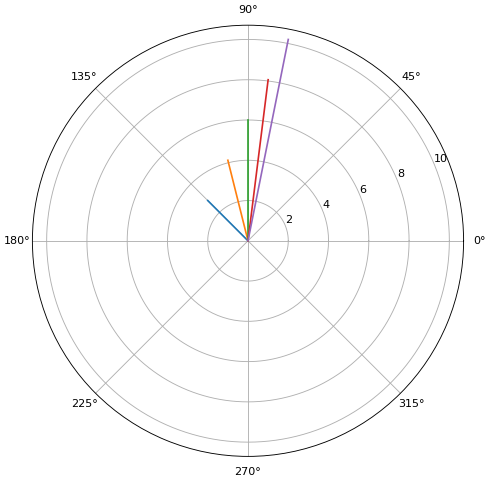
จะเห็นว่าได้กราฟออกมาเหมือนกัน
อ้างอิง
numpy มีคำสั่งต่างๆที่ช่วยในการจัดการกับจำนวนเชิงซ้อนภายในอาเรย์ทำให้การใช้งานทำได้สะดวก ซึ่งจะมาพูดถึงกันตรงนี้
สำหรับการจัดการกับจำนวนเชิงซ้อนในเบื้องต้นของภาษาไพธอนที่ไม่เกี่ยวกับ numpy อ่านได้ที่ https://phyblas.hinaboshi.com/20160608
การสร้างอาเรย์ของจำนวนเชิงซ้อน
ตอนที่ประกาศสร้างอาเรย์ขึ้นมาจากลิสต์หากมีสมาชิกเป็นจำนวนเชิงซ้อนแม้แต่ตัว เดียวก็จะได้ชนิดของอาเรย์เป็นจำนวนเชิงซ้อน สมาชิกตัวอื่นทั้งหมดก็จะเขียนอยู่ในรูปจำนวนเชิงซ้อนด้วย
import numpy as np
az = np.array([ 2, 1, 2+1j])
print(az) # ได้ [ 2.+0.j 1.+0.j 2.+1.j]
print(az.dtype) # ได้ dtype('complex128')
az = np.array([ 2, 1, 2+1j])
print(az) # ได้ [ 2.+0.j 1.+0.j 2.+1.j]
print(az.dtype) # ได้ dtype('complex128')
complex128 ในที่นี้เป็นชนิดข้อมูลจำนวนเชิงซ้อนมาตรฐานเมื่อสร้างจำนวนเชิงซ้อนขึ้นมา แล้วไม่กำหนดอะไรเพิ่มเติมก็จะได้ชนิดนี้ นอกจากนี้ยังมี complex64 กับ complex256 ด้วย สามารถกำหนดได้ตอนสร้าง
หรือหากสมาชิกเป็นจำนวนจริงแต่ระบุชนิดเป็นจำนวนเชิงซ้อนก็จะได้อาเรย์ของจำนวนเชิงซ้อนเช่นกัน
ay = np.array([3,4,5],dtype=complex)
print(ay) # ได้ [ 3.+0.j 4.+0.j 5.+0.j]
print(ay.dtype) # ได้ dtype('complex128')
print(ay) # ได้ [ 3.+0.j 4.+0.j 5.+0.j]
print(ay.dtype) # ได้ dtype('complex128')
หากระบุว่า complex เฉยๆจะได้ชนิด complex128 แต่ถ้าต้องการชนิด 'complex64' หรือ 'complex256' ก็ต้องระบุไปเป็นสายอักขระ
ay = np.array([3,4,5],dtype='complex64')
อาเรย์ของจำนวนจริงหากนำมาบวกกับจำนวนเชิงซ้อนก็จะเปลี่ยนได้ผลเป็น จำนวนเชิงซ้อนทันที จะใช้วิธีนี้ในการสร้างอาเรย์จำนวนเชิงซ้อนก็ได้
print(np.arange(1,8)+0j) # [ 1.+0.j 2.+0.j 3.+0.j 4.+0.j 5.+0.j 6.+0.j 7.+0.j]
เมื่ออาเรย์จำนวนจริงคูณกับจำนวนเชิงซ้อน ก็จะได้อาเรย์จำนวนเชิงซ้อนมา
print(np.arange(5)*1j) # ได้ [ 0.+0.j 0.+1.j 0.+2.j 0.+3.j 0.+4.j]
ดังนั้นอาจสร้างอาเรย์ของจำนวนเชิงซ้อนได้โดยการสร้างส่วนจริงและส่วนจินตภาพแยกกันแล้วนำมาบวกกันได้
az = np.arange(1,8)*3+np.arange(1,8)*4j
print(az) # ได้ [ 3. +4.j 6. +8.j 9.+12.j 12.+16.j 15.+20.j 18.+24.j 21.+28.j]
print(az) # ได้ [ 3. +4.j 6. +8.j 9.+12.j 12.+16.j 15.+20.j 18.+24.j 21.+28.j]
ต้องระวังว่าอาเรย์ของจำนวนจริงต่อให้นำมาคำนวณยังไงก็ไม่อาจได้จำนวนเชิงซ้อน เช่นต่อให้รู้ว่าจำนวนติดลบยกกำลังแล้วควรจะได้จำนวนเชิงซ้อนก็ตาม
ayy = np.arange(-3,2)
print(ayy) # ได้ [-3 -2 -1 0 1]
print(ayy**0.5) # ได้ [ nan nan nan 0. 1.]
print(ayy) # ได้ [-3 -2 -1 0 1]
print(ayy**0.5) # ได้ [ nan nan nan 0. 1.]
ลักษณะแบบนี้ไม่ว่าจะทำในไพธอน 3 หรือ 2 ก็ให้ผลแบบเดียวกัน
ดังนั้นจึงมีความจำเป็นต้องเปลี่ยนให้อยู่ในรูปเชิงซ้อนก่อน
print((ayy+0j)**0.5) # ได้ [ 0.+1.73205081j 0.+1.41421356j 0.+1.j 0.+0.j 1.+0.j ]
ส่วนจริง, ส่วนจินตภาพ และสังยุค
ในการหาค่าส่วนจริงและส่วนจินตภาพของจำนวนเชิงซ้อนในอาเรย์อาจใช้ฟังก์ชัน np.real และ np.imag หรืออาจจะดูค่าเป็นแอตทริบิวต์ real และ imag ก็ได้เช่นกัน
ayz = np.arange(3,9)+np.arange(1,7)*1j
print(np.real(ayz)) # ได้ [ 3. 4. 5. 6. 7. 8.]
print(np.imag(ayz)) # ได้ [ 1. 2. 3. 4. 5. 6.]
print(ayz.real) # ได้ [ 3. 4. 5. 6. 7. 8.]
print(ayz.imag) # ได้ [ 1. 2. 3. 4. 5. 6.]
print(np.real(ayz)) # ได้ [ 3. 4. 5. 6. 7. 8.]
print(np.imag(ayz)) # ได้ [ 1. 2. 3. 4. 5. 6.]
print(ayz.real) # ได้ [ 3. 4. 5. 6. 7. 8.]
print(ayz.imag) # ได้ [ 1. 2. 3. 4. 5. 6.]
ส่วนค่าสังยุคหาได้จาก ฟังก์ชัน np.conj หรืออาจใช้เมธอด conj ก็ได้ (เป็นเมธอด ไม่ใช่แอตทริบิวต์ ต้องมีวงเล็บด้วย)
print(ayz.conj()) # ได้ [ 3.-1.j 4.-2.j 5.-3.j 6.-4.j 7.-5.j 8.-6.j]
print(np.conj(ayz)) # ได้ [ 3.-1.j 4.-2.j 5.-3.j 6.-4.j 7.-5.j 8.-6.j]
print(np.conj(ayz)) # ได้ [ 3.-1.j 4.-2.j 5.-3.j 6.-4.j 7.-5.j 8.-6.j]
จำนวนเชิงซ้อนในรูปพิกัดเชิงขั้ว
จำนวนเชิงซ้อนอาจเขียนในรูปแบบเชิงขั้ว แสดงโดยค่าสัมบูรณ์ r และมุมเฟส θ ดังนี้

ค่าสัมบูรณ์หาได้โดยใช้ฟังก์ชัน np.abs หรือ np.absolute (ความจริงแล้วคือฟังก์ชันเดียวกัน np.abs เป็นแค่ชื่อย่อของ np.absolute)
azz = np.arange(-2,3)+np.arange(1,6)*2j
print(azz) # ได้ [-2. +2.j -1. +4.j 0. +6.j 1. +8.j 2.+10.j]
print(np.abs(azz)) # ได้ [ 2.82842712 4.12310563 6. 8.06225775 10.19803903]
print(azz) # ได้ [-2. +2.j -1. +4.j 0. +6.j 1. +8.j 2.+10.j]
print(np.abs(azz)) # ได้ [ 2.82842712 4.12310563 6. 8.06225775 10.19803903]
และมุมเฟสหาได้จากฟังก์ชัน np.angle
print(np.angle(azz)) # ได้ [ 2.35619449 1.81577499 1.57079633 1.44644133 1.37340077]
ลองนำมาวาดกราฟของแต่ละจุดโดยให้เส้นลากจากจุด 0 โดยให้แกนนอนเป็นส่วนจริงและแกนตั้งเป็นส่วนจินตภาพ
import matplotlib.pyplot as plt
plt.axes(xlim=[-7,8],ylim=[0,10])
for i in range(len(azz)):
plt.plot([0,azz[i].real],[0,azz[i].imag])
plt.show()
plt.axes(xlim=[-7,8],ylim=[0,10])
for i in range(len(azz)):
plt.plot([0,azz[i].real],[0,azz[i].imag])
plt.show()

ลองเขียนในรูปพิกัดเชิงขั้วโดยใช้ค่าสัมบูรณ์และมุมเฟส
plt.axes(polar=1)
for i in range(len(azz)):
plt.plot([0,np.angle(azz[i])],[0,np.abs(azz[i])])
plt.show()
for i in range(len(azz)):
plt.plot([0,np.angle(azz[i])],[0,np.abs(azz[i])])
plt.show()

จะเห็นว่าได้กราฟออกมาเหมือนกัน
อ้างอิง
http://pythonscience.blogspot.com/2014/05/blog-post_9.html
http://www.kamishima.net/mlmpyja/nbayes1/ndarray.html
http://oppython.hatenablog.com/entry/2015/01/19/172201
http://www.kamishima.net/mlmpyja/nbayes1/ndarray.html
http://oppython.hatenablog.com/entry/2015/01/19/172201