pytorch เบื้องต้น บทที่ ๖: การวิเคราะห์การถดถอยโลจิสติก
เขียนเมื่อ 2018/09/08 09:58
แก้ไขล่าสุด 2022/07/09 18:01
>> ต่อจาก บทที่ ๕
ในบทนี้จะเป็นการใช้ pytorch เพื่อสร้างเพอร์เซปตรอนสำหรับทำการถดถอยโลจิสติกอย่างง่าย
การถดถอยโลจิสติกเพื่อจำแนกประเภทข้อมูล ๒ กลุ่ม
ขอยกตัวอย่างเป็นปัญหาปัญหาการแบ่งประเภทข้อมูลสองตัวแปรง่ายๆดังนี้
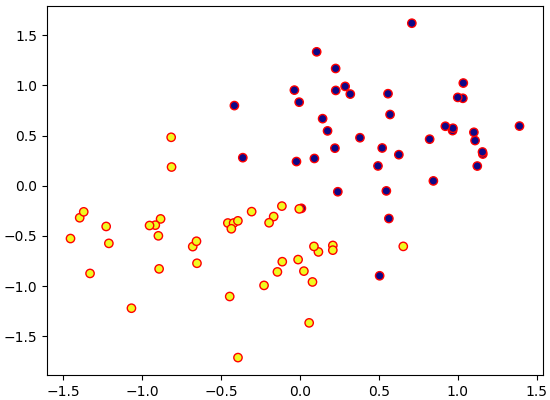
การคำนวณในปัญหาการแบ่งประเภทแบบนี้โดยทั่วไปจะเริ่มจากชั้นคูณเชิงเส้น แล้วตามด้วยซิกมอยด์ แล้วหาค่าเสียหายซึ่งในกรณีนี้ใช้เป็นค่าเอนโทรปีไขว้ (交叉熵, cross entropy) เฉลี่ย
..(6.1)
สมการนี้ต่างจากใน โครงข่ายประสาทเทียมเบื้องต้นบทที่ ๔ ตรงที่ w กลายเป็น wT เนื่องจากนิยามของค่าน้ำหนักใน pytorch จะกลับกัน คือเอาค่าขาออกเป็นแนวตั้ง ขาเข้าเป็นแนวนอน
โดยทั่วไปชั้นการคำนวณซิกมอยด์กับเอนโทรปีไขว้จะถูกยุบรวมเป็นชั้นเดียวเพราะสะดวกในการคำนวณ
ใน pytorch เองก็มีเตรียมชั้นสำหรับคำนวณแบบนี้ไว้ คือคลาส torch.nn.BCEWithLogitsLoss หรือจะใช้ฟังก์ชัน torch.nn.functional.binary_cross_entropy_with_logits() ก็ได้
สามารถเขียนโค้ดเพื่อทำการจำแนกกลุ่มข้อมูลได้ดังนี้
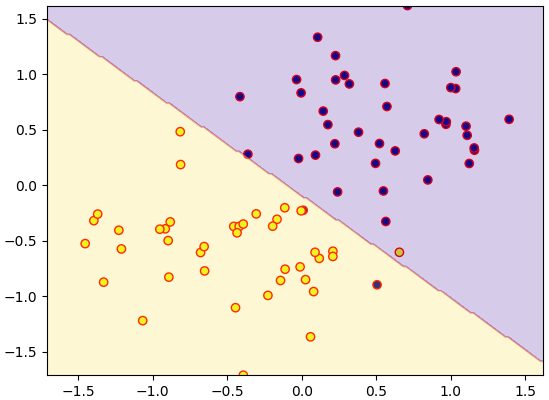
ตรงนี้จะเห็นว่าคล้ายกับตอนที่แก้ปัญหาการถดถอยเชิงเส้นมาก ต่างกันแค่เปลี่ยนฟังก์ชันค่าเสียหายจากค่าผลต่างกำลังสองเฉลี่ยมาเป็นเอนโทรปีไขว้เฉลี่ยเท่านั้น
ข้อควรระวังอย่างหนึ่งก็คือ BCEWithLogitsLoss นี้ต้องใช้กับเทนเซอร์ชนิด float เท่านั้น แม้ว่าจริงๆแล้วค่า z ของเราปกติจะเป็นได้แค่เลข 0 หรือ 1 เท่านั้นจนบางคนอาจคิดว่าใช้ ByteTensor หรือ IntTensor ก็น่าจะได้ก็ตาม แต่จริงๆใช้ไม่ได้
นี่ถือเป็นความไม่สะดวกอย่างหนึ่งของ pytorch ชนิดข้อมูลที่ใช้สำหรับบางฟังก์ชันมักจะถูกกำหนดตายตัว ไม่มีการเปลี่ยนให้อัตโนมัติ
หากต้องการหาค่าความน่าจะเป็นของคำตอบ pytorch ก็มีฟังก์ชัน torch.sigmoid เตรียมไว้ให้ หรือคลาส torch.nn.Sigmoid() ใช้ได้เลยไม่ต้องสร้างเอง
ลองวาดคอนทัวร์แสดงความน่าจะเป็น
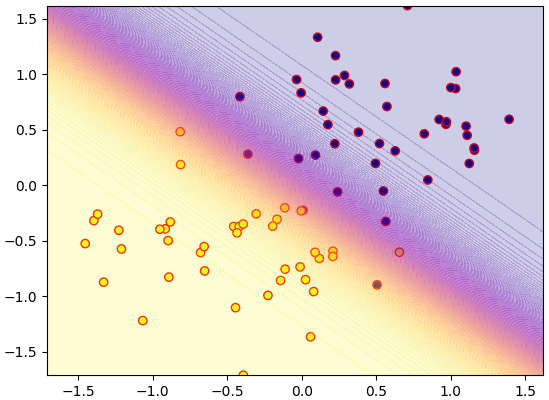
การถดถอยโลจิสติกเพื่อจำแนกประเภทหลายกลุ่ม
ต่อมาพิจารณาปัญหาการจำแนกประเภทที่มากกว่า ๒ กลุ่ม หรือที่เรียกว่าการวิเคราะห์การถดถอยซอฟต์แม็กซ์
การคำนวณในกรณีนี้จะเริ่มจากการคำนวณเชิงเส้นแล้วตามด้วยฟังก์ชันซอฟต์แม็กซ์แล้วคำนวณค่าเสียหายด้วยเอนโทรปีไขว้สำหรับข้อมูลหลายกลุ่ม
..(6.2)
สมการนี้ก็ต่างจากในเนื้อหาโครงข่ายประสาทเทียมเบื้องต้นบทที่ ๖ เล็กน้อยเนื่องจากแกนของ w สลับกัน
lin ในที่นี้เราต้องการจำแนกข้อมูล 2 ตัวแปรเป็น 4 กลุ่ม ดังนั้นต้องมีขนาดขาเข้าเป็น 2 ขนาดขาออกเป็น 4 ส่วนขนาดของค่าน้ำหนัก w จะเป็น (4,2)
pytorch ได้เตรียมคลาสสำหรับคำนวณซอฟต์แม็กซ์พร้อมกับเอนโทรปีไขว้ให้ในทีเดียวคือ torch.nn.CrossEntropyLoss หรือในรูปฟังก์ชันคือ torch.nn.functional.cross_entropy()
ค่าที่ต้องส่งให้ฟังก์ชันนี้ก็คือค่าที่ได้การคำนวณเชิงเส้น (ในสมการคือ a) และค่าคำตอบจริงในรูปของตัวเลขบอกประเภท ไม่ใช่ในรูปของวันฮ็อต ดังนั้นถ้าใช้ฟังก์ชันนี้เราจะไม่ต้องต้องอุตส่าห์แปลงคำตอบให้เป็นวันฮ็อตเอง
โค้ดเขียนได้ดังนี้
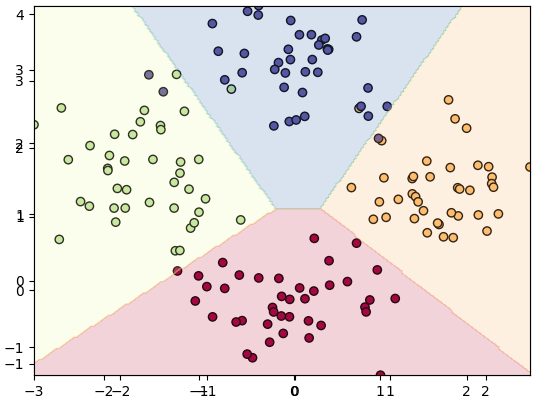
ข้อแตกต่างจากกรณีแบ่ง ๒ กลุ่มคือขนาดของ lin และฟังก์ชันที่ใช้คำนวณเอนโทรปีไขว้
นอกจากนี้ที่ต้องระวังคือ ค่า z ในที่นี้ต้องเป็น LongTensor ซึ่งจะต่างจากกรณีของ BCEWithLogitsLoss
>> อ่านต่อ บทที่ ๗
ในบทนี้จะเป็นการใช้ pytorch เพื่อสร้างเพอร์เซปตรอนสำหรับทำการถดถอยโลจิสติกอย่างง่าย
การถดถอยโลจิสติกเพื่อจำแนกประเภทข้อมูล ๒ กลุ่ม
ขอยกตัวอย่างเป็นปัญหาปัญหาการแบ่งประเภทข้อมูลสองตัวแปรง่ายๆดังนี้
import numpy as np
import matplotlib.pyplot as plt
X = np.random.normal(-0.5,0.4,[80,2])
X[:40] += 1
z = np.array([0,1]).repeat(40)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='r',cmap='plasma')
plt.show()
การคำนวณในปัญหาการแบ่งประเภทแบบนี้โดยทั่วไปจะเริ่มจากชั้นคูณเชิงเส้น แล้วตามด้วยซิกมอยด์ แล้วหาค่าเสียหายซึ่งในกรณีนี้ใช้เป็นค่าเอนโทรปีไขว้ (交叉熵, cross entropy) เฉลี่ย
..(6.1)
สมการนี้ต่างจากใน โครงข่ายประสาทเทียมเบื้องต้นบทที่ ๔ ตรงที่ w กลายเป็น wT เนื่องจากนิยามของค่าน้ำหนักใน pytorch จะกลับกัน คือเอาค่าขาออกเป็นแนวตั้ง ขาเข้าเป็นแนวนอน
โดยทั่วไปชั้นการคำนวณซิกมอยด์กับเอนโทรปีไขว้จะถูกยุบรวมเป็นชั้นเดียวเพราะสะดวกในการคำนวณ
ใน pytorch เองก็มีเตรียมชั้นสำหรับคำนวณแบบนี้ไว้ คือคลาส torch.nn.BCEWithLogitsLoss หรือจะใช้ฟังก์ชัน torch.nn.functional.binary_cross_entropy_with_logits() ก็ได้
สามารถเขียนโค้ดเพื่อทำการจำแนกกลุ่มข้อมูลได้ดังนี้
import torch
X = torch.Tensor(X)
z = torch.Tensor(z)
lin = torch.nn.Linear(2,1)
opt = torch.optim.Adam(lin.parameters(),lr=0.1)
ha_entropy = torch.nn.BCEWithLogitsLoss() # เตรียมฟังก์ชันคำนวณเอนโทรปี
for i in range(100):
a = lin(X).flatten()
J = ha_entropy(a,z)
J.backward()
opt.step()
opt.zero_grad()
lmm = np.linspace(X.min(),X.max(),200)
mx,my = np.meshgrid(lmm,lmm)
mX = torch.Tensor(np.array([mx.ravel(),my.ravel()]).T)
mz = (lin(mX)>0)
mz = mz.data.numpy().reshape(200,200)
plt.xlim(X.min(),X.max())
plt.ylim(X.min(),X.max())
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='r',cmap='plasma')
plt.contourf(mx,my,mz,alpha=0.2,cmap='plasma')
plt.show()
ตรงนี้จะเห็นว่าคล้ายกับตอนที่แก้ปัญหาการถดถอยเชิงเส้นมาก ต่างกันแค่เปลี่ยนฟังก์ชันค่าเสียหายจากค่าผลต่างกำลังสองเฉลี่ยมาเป็นเอนโทรปีไขว้เฉลี่ยเท่านั้น
ข้อควรระวังอย่างหนึ่งก็คือ BCEWithLogitsLoss นี้ต้องใช้กับเทนเซอร์ชนิด float เท่านั้น แม้ว่าจริงๆแล้วค่า z ของเราปกติจะเป็นได้แค่เลข 0 หรือ 1 เท่านั้นจนบางคนอาจคิดว่าใช้ ByteTensor หรือ IntTensor ก็น่าจะได้ก็ตาม แต่จริงๆใช้ไม่ได้
นี่ถือเป็นความไม่สะดวกอย่างหนึ่งของ pytorch ชนิดข้อมูลที่ใช้สำหรับบางฟังก์ชันมักจะถูกกำหนดตายตัว ไม่มีการเปลี่ยนให้อัตโนมัติ
หากต้องการหาค่าความน่าจะเป็นของคำตอบ pytorch ก็มีฟังก์ชัน torch.sigmoid เตรียมไว้ให้ หรือคลาส torch.nn.Sigmoid() ใช้ได้เลยไม่ต้องสร้างเอง
ลองวาดคอนทัวร์แสดงความน่าจะเป็น
mz = torch.nn.Sigmoid()(lin(mX))
mz = mz.data.numpy().reshape(200,200)
plt.xlim(X.min(),X.max())
plt.ylim(X.min(),X.max())
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='r',cmap='plasma')
plt.contourf(mx,my,mz,200,alpha=0.2,cmap='plasma')
plt.show()
การถดถอยโลจิสติกเพื่อจำแนกประเภทหลายกลุ่ม
ต่อมาพิจารณาปัญหาการจำแนกประเภทที่มากกว่า ๒ กลุ่ม หรือที่เรียกว่าการวิเคราะห์การถดถอยซอฟต์แม็กซ์
การคำนวณในกรณีนี้จะเริ่มจากการคำนวณเชิงเส้นแล้วตามด้วยฟังก์ชันซอฟต์แม็กซ์แล้วคำนวณค่าเสียหายด้วยเอนโทรปีไขว้สำหรับข้อมูลหลายกลุ่ม
..(6.2)
สมการนี้ก็ต่างจากในเนื้อหาโครงข่ายประสาทเทียมเบื้องต้นบทที่ ๖ เล็กน้อยเนื่องจากแกนของ w สลับกัน
lin ในที่นี้เราต้องการจำแนกข้อมูล 2 ตัวแปรเป็น 4 กลุ่ม ดังนั้นต้องมีขนาดขาเข้าเป็น 2 ขนาดขาออกเป็น 4 ส่วนขนาดของค่าน้ำหนัก w จะเป็น (4,2)
pytorch ได้เตรียมคลาสสำหรับคำนวณซอฟต์แม็กซ์พร้อมกับเอนโทรปีไขว้ให้ในทีเดียวคือ torch.nn.CrossEntropyLoss หรือในรูปฟังก์ชันคือ torch.nn.functional.cross_entropy()
ค่าที่ต้องส่งให้ฟังก์ชันนี้ก็คือค่าที่ได้การคำนวณเชิงเส้น (ในสมการคือ a) และค่าคำตอบจริงในรูปของตัวเลขบอกประเภท ไม่ใช่ในรูปของวันฮ็อต ดังนั้นถ้าใช้ฟังก์ชันนี้เราจะไม่ต้องต้องอุตส่าห์แปลงคำตอบให้เป็นวันฮ็อตเอง
โค้ดเขียนได้ดังนี้
X = np.random.normal(0,0.5,[160,2])
X[40:] += 1.5
X[80:,0] -= 3
X[120:] += 1.5
z = np.arange(4).repeat(40)
X = torch.Tensor(X)
z = torch.LongTensor(z)
lin = torch.nn.Linear(2,4)
opt = torch.optim.Adam(lin.parameters(),lr=0.1)
ha_entropy = torch.nn.CrossEntropyLoss()
for i in range(100):
a = lin(X)
J = ha_entropy(a,z)
J.backward()
opt.step()
opt.zero_grad()
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),
np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = torch.Tensor(np.array([mx.ravel(),my.ravel()]).T)
mz = lin(mX).argmax(1)
mz = mz.data.numpy().reshape(200,200)
plt.xlim(X[:,0].min(),X[:,0].max())
plt.ylim(X[:,1].min(),X[:,1].max())
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='Spectral')
plt.contourf(mx,my,mz,alpha=0.2,cmap='Spectral')
plt.show()
ข้อแตกต่างจากกรณีแบ่ง ๒ กลุ่มคือขนาดของ lin และฟังก์ชันที่ใช้คำนวณเอนโทรปีไขว้
นอกจากนี้ที่ต้องระวังคือ ค่า z ในที่นี้ต้องเป็น LongTensor ซึ่งจะต่างจากกรณีของ BCEWithLogitsLoss
>> อ่านต่อ บทที่ ๗
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> pytorch