โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๖: การวิเคราะห์จำแนกประเภทหลายกลุ่ม
เขียนเมื่อ 2018/08/26 23:25
แก้ไขล่าสุด 2022/07/10 21:11
>> ต่อจาก บทที่ ๕
ในบทก่อนหน้านี้เราพิจารณาปัญหาการจำแนกประเภทข้อมูลที่มีแค่ ๒ กลุ่ม
คราวนี้จะมาพิจารณาปัญหาที่ซับซ้อนขึ้น นั่นคือการวิเคราะห์จำแนกประเภทข้อมูลหลายๆกลุ่มที่ไม่ใช่แค่ ๒
หลักการ
เดิมทีในปัญหาการจำแนกประเภทเป็น ๒ กลุ่มนั้นเราใช้เพอร์เซปตรอนที่ให้คำตอบออกมาแค่ค่าเดียวแล้วดูว่าคำตอบมากกว่าหรือน้อยกว่า 0 แล้วตัดสินจำแนก ๒ กลุ่มจากตรงนี้
แต่พอมี ๓ กลุ่มขึ้นไปจะทำแบบนี้ไม่ได้แล้ว แต่ต้องเปลี่ยนวิธีการใหม่ นั่นคือแทนที่จะคำนวณให้ผลลัพธ์แค่ค่าเดียว ต้องเปลี่ยนมาเป็นให้ออกมาเป็นจำนวนเท่ากับจำนวนประเภทที่ต้องการจำแนก แล้วเทียบดูว่าตัวไหนมากที่สุดก็ตัดสินว่าเป็นกลุ่มนั้น
สมมุติว่าข้อมูลมี ๔ ตัวแปร ต้องการแบ่ง ๕ กลุ่ม การคำนวณของข้อมูลจะเป็นไปในลักษณะนี้
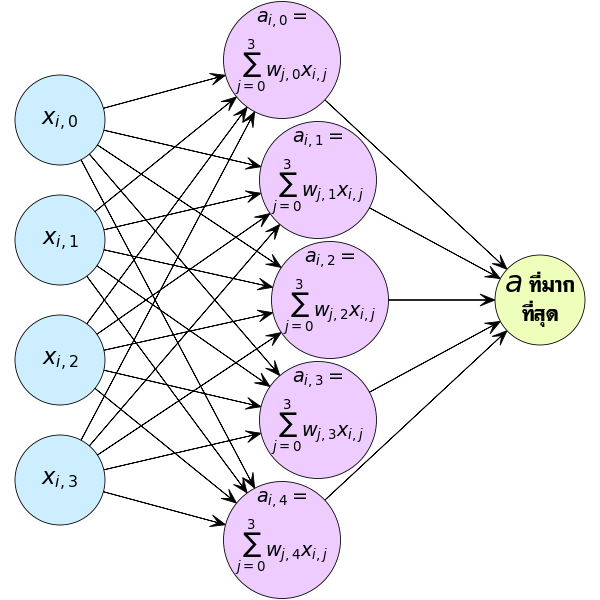
(ในที่นี้มีการใส่ดัชนี i ซึ่งแสดงถึงลำดับของข้อมูลด้วย เพราะข้อมูลที่ป้อนเข้าไปไม่ได้มีแค่ตัวเดียว สมการนี้แสดงการคำนวณของข้อมูลตัวที่ i)
ตัวแปรต้นแต่ละตัวต้องไปคูณกับค่าน้ำหนักของแต่ละกลุ่มแยกต่างหากกัน ตรงนี้ทำให้ w กลายเป็นอาเรย์สองมิติ ในที่นี้มีขนาด 4×5 ส่วน b ก็กลายเป็นมีหลายตัว จำนวนเท่ากับจำนวนกลุ่มประเภทที่แยก คือ 5
การคำนวณหาค่า a อาจเขียนในรูปของการคูณเมทริกซ์ได้ว่า
..(6.1)
ในที่นี้ m0 เป็นจำนวนตัวแปรต้น หรือก็คือจำนวนมิติข้อมูลขาเข้า m1 เป็นจำนวนกลุ่มที่แบ่ง ซึ่งก็คือจำนวนมิติของค่าขาออก
อาเรย์ค่าน้ำหนัก w มีขนาดเป็น m0×m1 ทำหน้าที่เป็นตัวเปลี่ยนถ่ายระหว่างข้อมูลขาเข้ากับขาออก
ทั้ง a และ x เองก็เป็นข้อมูลหลายค่าหลายตัวแปร ดังนั้นจึงอยู่ในรูปของอาเรย์สองมิติ เขียนการคำนวณใหม่ได้ดังนี้
..(6.2)
โดย a คือ
..(6.3)
จะเห็นว่าขนาดของ a, x, w สอดคล้องกันดี [n,m1] = [n,m0][m0,m1]
ส่วน b เป็นอาเรย์หนึ่งมิติ แต่เวลานำมาบวกกันจะเท่ากับเป็นการบวกทุกแถว ตามคุณสมบัติของอาเรย์
..(6.4)
ต่อมาเมื่อได้ค่า a แล้วก็ดูว่าค่าไหนหลักไหนในแต่ละแถวมีค่ามากสุด คำตอบก็คือกลุ่มนั้นสำหรับในแถวนั้น
ในไพธอนใช้ .argmax เพื่อหาว่าแถวไหนมีค่าสูงสุดได้ โดยต้องระบุแกนเป็น axis=1 จะได้ค่าสูงสุดในแต่ละแถว
ได้
ส่วนการหาความน่าจะเป็นนั้นหากเดิมทีตอนที่แบ่งเป็นสองกลุ่มจะใช้ฟังก์ชันซิกมอยด์ แต่สำหรับในกรณีหลายกลุ่มแบบนี้จะเปลี่ยนมาใช้ฟังก์ชันซอฟต์แม็กซ์ (softmax) แทน
สามารถคำนวณได้ดังนี้
..(6.5)
หรือเขียนในรูปของแต่ละค่าได้เป็น
..(6.6)
ค่าที่ได้จากฟังก์ชันซอฟต์แม็กซ์แต่ละแถวจะบวกกันแล้วได้ 1 ดังนั้นจึงใช้แทนค่าความน่าจะเป็นของแต่ละตัว ในทำนองเดียวกับซิกมอยด์
ตัวอย่างการใช้ฟังก์ชันซอฟต์แม็กซ์ในไพธอน
ได้
จากนั้นเวลาคำนวณค่าเสียหายก็ใช้ค่าเอนโทรปีไขว้เช่นเดียวกัน แต่วิธีการคำนวณจะกลายเป็นแบบนี้
..(6.7)
โดยที่ z ในที่นี้คือค่าคำตอบในรูปของวันฮ็อต (one-hot)
คือแทนค่าคำตอบเป็นเลขแทนกลุ่มแต่ละกลุ่ม ก็เขียนในรูปของอาเรย์สองมิติที่มีค่าเป็น 1 อยู่ค่าเดียวในตำแหน่งของกลุ่มที่เป็นคำตอบ ส่วนที่เหลือเป็น 0
ในไพธอนอาจเขียนฟังก์ชันแปลงได้ง่ายๆแบบนี้
ได้
ฟังก์ชันที่สร้างขึ้นนี้จะทำการแปลงเป็นอาเรย์ที่ประกอบด้วย True False ถ้าจะแปลงเป็นเลข 1 และ 0 อีกทีก็เติม .astype(int) ต่อท้ายได้ แต่ว่าในทางปฏิบัติแล้วไม่จำเป็น ให้อยู่ในรูป True False แบบนี้จะสะดวกมากกว่า เวลาใช้ในการคำนวณจะถูกแปลงเป็น 1 0 โดยอัตโนมัติ
สำหรับรายละเอียดของเรื่องเอนโทรปีไขว้และที่มาของวิธีคำนวณอ่านได้ใน https://phyblas.hinaboshi.com/20180814
เพื่อที่จะทำการแพร่ย้อนกลับเพื่อหาอนุพันธ์ของค่าน้ำหนักและไบแอส อาจเขียนกราฟคำนวณได้ดังนี้
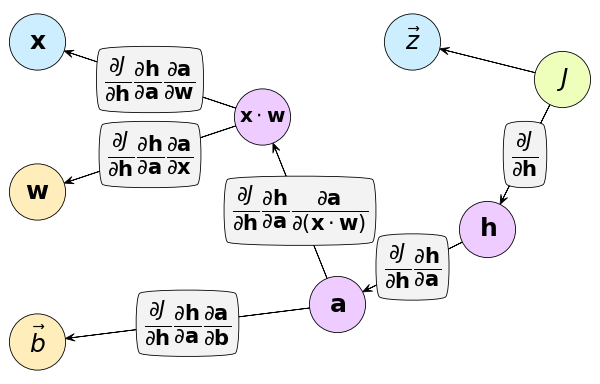
การคำนวณก็จะคล้ายๆกับในบทที่ ๔ จึงขอละรายละเอียด โดยรวมแล้วเขียนได้ดังนี้
..(6.8)
แทนลงในกราฟคำนวณ
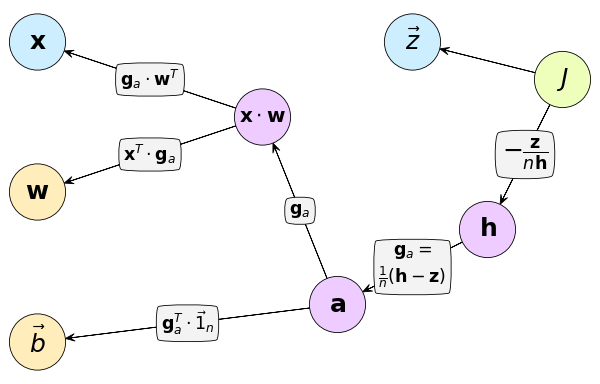
และนำค่าอนุพันธ์มาใช้ปรับค่าน้ำหนักและไบแอสเหมือนเดิม
..(6.9)
เขียนโปรแกรม
อาจสร้างคลาสของโครงข่ายประสาทเทียมสำหรับจำแนกประเภทข้อมูลหลายกลุ่มได้ดังนี้
วิธีการใช้ก็เหมือนกับแบบที่แบ่ง ๒ กลุ่มในบทที่ ๔ เพียงแต่ z ในที่นี้ไม่ได้มีแค่ 0 และ 1 แต่เป็นจำนวนเต็มตั้งแต่ 0 ไปจนถึงจำนวนกลุ่ม-1 แล้วในระห่างเรียนรู้จะถูกแปลงเป็นอาเรย์แบบวันฮ็อตเพื่อใช้ตอนคำนวณเอนโทรปี
ในที่นี้สร้างให้ใช้กับการแบ่งกี่กลุ่มก็ได้ โดยให้หาจำนวนกลุ่มง่ายๆโดยดูจากค่าสูงสุด
ลองนำมาใช้จำแนกข้อมูลที่มี ๓ กลุ่มแบบนี้
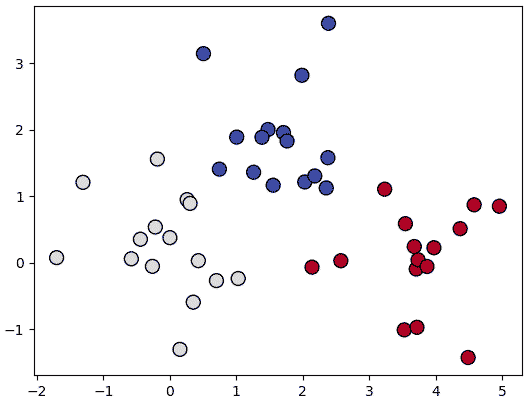
ให้โครงข่ายประสาทของเราทำการเรียนรู้แล้วทำนายแบ่งเขตพื้นที่ออกมา
เอนโทรปีและคะแนนก็ได้บันทึกไว้ เอาออกมาดูความคืบหน้าในการเรียนรู้ได้
สุดท้ายลองทดสอบกับข้อมูลรูปร่างต่างๆเช่นเดียวกับในบทที่ ๔ (โหลด >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar)
แต่คราวนี้เราสามารถแบ่งทุกกลุ่มได้แล้ว จึงจะใช้รูปทั้ง ๕ ชนิด

ลองให้โปรแกรมทำการเรียนรู้แล้วก็แสดงความคืบหน้าของความแม่นยำในการทำนาย
ดูแล้วจะเห็นว่าทายได้ถูกต้องได้แค่ 80% เท่านั้น
เพื่อจะเห็นว่าปัญหาอยู่ตรงไหนอาจลองวาดเมทริกซ์ความสับสนดู
รายละเอียดเกี่ยวกับเรื่องนี้ขอละไว้ อ่านได้ใน https://phyblas.hinaboshi.com/20170926
เขียนฟังก์ชันเมทริกซ์ความสับสน แล้วใช้ดู
ดูแล้วจะเห็นว่าโปรแกรมมีปัญหาในการแยกแยะประเภทที่ 0 (วงกลม) กับประเภทที่ 2 (สี่เหลี่ยม)
ที่เป็นอย่างนี้ก็เพราะโครงข่ายประสาทที่มีแค่ชั้นเดียวแบบนี้เป็นแค่การแบ่งเชิงเส้นอย่างง่าย ทำได้แค่พิจารณาง่ายๆว่ารูปแบบไหนมีการขีดที่จุดไหนมากๆ ไม่ได้คิดอะไรซับซ้อน
เพื่อที่จะพิจารณาปัญหาที่ซับซ้อนขึ้นได้จำเป็นต้องสร้างโครงข่ายที่ต่อกัน ๒ ชั้นขึ้นไป ซึ่งจะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๗
ในบทก่อนหน้านี้เราพิจารณาปัญหาการจำแนกประเภทข้อมูลที่มีแค่ ๒ กลุ่ม
คราวนี้จะมาพิจารณาปัญหาที่ซับซ้อนขึ้น นั่นคือการวิเคราะห์จำแนกประเภทข้อมูลหลายๆกลุ่มที่ไม่ใช่แค่ ๒
หลักการ
เดิมทีในปัญหาการจำแนกประเภทเป็น ๒ กลุ่มนั้นเราใช้เพอร์เซปตรอนที่ให้คำตอบออกมาแค่ค่าเดียวแล้วดูว่าคำตอบมากกว่าหรือน้อยกว่า 0 แล้วตัดสินจำแนก ๒ กลุ่มจากตรงนี้
แต่พอมี ๓ กลุ่มขึ้นไปจะทำแบบนี้ไม่ได้แล้ว แต่ต้องเปลี่ยนวิธีการใหม่ นั่นคือแทนที่จะคำนวณให้ผลลัพธ์แค่ค่าเดียว ต้องเปลี่ยนมาเป็นให้ออกมาเป็นจำนวนเท่ากับจำนวนประเภทที่ต้องการจำแนก แล้วเทียบดูว่าตัวไหนมากที่สุดก็ตัดสินว่าเป็นกลุ่มนั้น
สมมุติว่าข้อมูลมี ๔ ตัวแปร ต้องการแบ่ง ๕ กลุ่ม การคำนวณของข้อมูลจะเป็นไปในลักษณะนี้

(ในที่นี้มีการใส่ดัชนี i ซึ่งแสดงถึงลำดับของข้อมูลด้วย เพราะข้อมูลที่ป้อนเข้าไปไม่ได้มีแค่ตัวเดียว สมการนี้แสดงการคำนวณของข้อมูลตัวที่ i)
ตัวแปรต้นแต่ละตัวต้องไปคูณกับค่าน้ำหนักของแต่ละกลุ่มแยกต่างหากกัน ตรงนี้ทำให้ w กลายเป็นอาเรย์สองมิติ ในที่นี้มีขนาด 4×5 ส่วน b ก็กลายเป็นมีหลายตัว จำนวนเท่ากับจำนวนกลุ่มประเภทที่แยก คือ 5
การคำนวณหาค่า a อาจเขียนในรูปของการคูณเมทริกซ์ได้ว่า
..(6.1)
ในที่นี้ m0 เป็นจำนวนตัวแปรต้น หรือก็คือจำนวนมิติข้อมูลขาเข้า m1 เป็นจำนวนกลุ่มที่แบ่ง ซึ่งก็คือจำนวนมิติของค่าขาออก
อาเรย์ค่าน้ำหนัก w มีขนาดเป็น m0×m1 ทำหน้าที่เป็นตัวเปลี่ยนถ่ายระหว่างข้อมูลขาเข้ากับขาออก
ทั้ง a และ x เองก็เป็นข้อมูลหลายค่าหลายตัวแปร ดังนั้นจึงอยู่ในรูปของอาเรย์สองมิติ เขียนการคำนวณใหม่ได้ดังนี้
..(6.2)
โดย a คือ
..(6.3)
จะเห็นว่าขนาดของ a, x, w สอดคล้องกันดี [n,m1] = [n,m0][m0,m1]
ส่วน b เป็นอาเรย์หนึ่งมิติ แต่เวลานำมาบวกกันจะเท่ากับเป็นการบวกทุกแถว ตามคุณสมบัติของอาเรย์
..(6.4)
ต่อมาเมื่อได้ค่า a แล้วก็ดูว่าค่าไหนหลักไหนในแต่ละแถวมีค่ามากสุด คำตอบก็คือกลุ่มนั้นสำหรับในแถวนั้น
ในไพธอนใช้ .argmax เพื่อหาว่าแถวไหนมีค่าสูงสุดได้ โดยต้องระบุแกนเป็น axis=1 จะได้ค่าสูงสุดในแต่ละแถว
import numpy as np
a = np.random.randint(-9,9,[4,5])
print(a)
print(a.argmax(1)) # หรือ a.argmax(axis=1)ได้
[[-4 -2 -9 -1 -8]
[ 2 6 6 -8 8]
[ 8 2 -3 5 5]
[-9 -2 7 -5 -6]]
[3 4 0 2]ส่วนการหาความน่าจะเป็นนั้นหากเดิมทีตอนที่แบ่งเป็นสองกลุ่มจะใช้ฟังก์ชันซิกมอยด์ แต่สำหรับในกรณีหลายกลุ่มแบบนี้จะเปลี่ยนมาใช้ฟังก์ชันซอฟต์แม็กซ์ (softmax) แทน
สามารถคำนวณได้ดังนี้
..(6.5)
หรือเขียนในรูปของแต่ละค่าได้เป็น
..(6.6)
ค่าที่ได้จากฟังก์ชันซอฟต์แม็กซ์แต่ละแถวจะบวกกันแล้วได้ 1 ดังนั้นจึงใช้แทนค่าความน่าจะเป็นของแต่ละตัว ในทำนองเดียวกับซิกมอยด์
ตัวอย่างการใช้ฟังก์ชันซอฟต์แม็กซ์ในไพธอน
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
a = np.random.randint(-9,9,[4,3])
print(a)
h = softmax(a)
print(h)
print(h.sum(1))ได้
[[ 3 3 7]
[-8 1 5]
[ 3 0 -7]
[ 8 6 7]]
[[ 1.76684220e-02 1.76684220e-02 9.64663156e-01]
[ 2.21966972e-06 1.79861700e-02 9.82011610e-01]
[ 9.52532933e-01 4.74238222e-02 4.32449282e-05]
[ 6.65240956e-01 9.00305732e-02 2.44728471e-01]]
[ 1. 1. 1. 1.]จากนั้นเวลาคำนวณค่าเสียหายก็ใช้ค่าเอนโทรปีไขว้เช่นเดียวกัน แต่วิธีการคำนวณจะกลายเป็นแบบนี้
..(6.7)
โดยที่ z ในที่นี้คือค่าคำตอบในรูปของวันฮ็อต (one-hot)
คือแทนค่าคำตอบเป็นเลขแทนกลุ่มแต่ละกลุ่ม ก็เขียนในรูปของอาเรย์สองมิติที่มีค่าเป็น 1 อยู่ค่าเดียวในตำแหน่งของกลุ่มที่เป็นคำตอบ ส่วนที่เหลือเป็น 0
ในไพธอนอาจเขียนฟังก์ชันแปลงได้ง่ายๆแบบนี้
def ha_1h(z,n):
return (z[:,None]==range(n))
z = np.random.randint(0,5,8)
print(z)
print(ha_1h(z,5))
print(ha_1h(z,5).astype(int)) # เปลี่ยนเป็นเลข 1 และ 0ได้
[1 3 0 2 2 1 4 0]
[[False True False False False]
[False False False True False]
[ True False False False False]
[False False True False False]
[False False True False False]
[False True False False False]
[False False False False True]
[ True False False False False]]
[[0 1 0 0 0]
[0 0 0 1 0]
[1 0 0 0 0]
[0 0 1 0 0]
[0 0 1 0 0]
[0 1 0 0 0]
[0 0 0 0 1]
[1 0 0 0 0]]ฟังก์ชันที่สร้างขึ้นนี้จะทำการแปลงเป็นอาเรย์ที่ประกอบด้วย True False ถ้าจะแปลงเป็นเลข 1 และ 0 อีกทีก็เติม .astype(int) ต่อท้ายได้ แต่ว่าในทางปฏิบัติแล้วไม่จำเป็น ให้อยู่ในรูป True False แบบนี้จะสะดวกมากกว่า เวลาใช้ในการคำนวณจะถูกแปลงเป็น 1 0 โดยอัตโนมัติ
สำหรับรายละเอียดของเรื่องเอนโทรปีไขว้และที่มาของวิธีคำนวณอ่านได้ใน https://phyblas.hinaboshi.com/20180814
เพื่อที่จะทำการแพร่ย้อนกลับเพื่อหาอนุพันธ์ของค่าน้ำหนักและไบแอส อาจเขียนกราฟคำนวณได้ดังนี้

การคำนวณก็จะคล้ายๆกับในบทที่ ๔ จึงขอละรายละเอียด โดยรวมแล้วเขียนได้ดังนี้
..(6.8)
แทนลงในกราฟคำนวณ

และนำค่าอนุพันธ์มาใช้ปรับค่าน้ำหนักและไบแอสเหมือนเดิม
..(6.9)
เขียนโปรแกรม
อาจสร้างคลาสของโครงข่ายประสาทเทียมสำหรับจำแนกประเภทข้อมูลหลายกลุ่มได้ดังนี้
import numpy as np
import matplotlib.pyplot as plt
def ha_entropy(z,h):
return -(np.log(h[z]+1e-10)).mean()
class Prasat:
def __init__(self,eta):
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.kiklum = int(z.max()+1)
Z = ha_1h(z,self.kiklum)
self.w = np.zeros([X.shape[1],self.kiklum])
self.b = np.zeros(self.kiklum)
self.entropy = []
self.khanaen = []
for i in range(n_thamsam):
a = self.ha_a(X)
h = softmax(a)
J = ha_entropy(Z,h)
ga = (h-Z)/len(z)
self.w -= self.eta*np.dot(X.T,ga)
self.b -= self.eta*ga.sum(0)
self.entropy.append(J)
khanaen = (h.argmax(1)==z).mean()
self.khanaen.append(khanaen)
def thamnai(self,X):
return self.ha_a(X).argmax(1)
def ha_a(self,X):
return np.dot(X,self.w) + self.bวิธีการใช้ก็เหมือนกับแบบที่แบ่ง ๒ กลุ่มในบทที่ ๔ เพียงแต่ z ในที่นี้ไม่ได้มีแค่ 0 และ 1 แต่เป็นจำนวนเต็มตั้งแต่ 0 ไปจนถึงจำนวนกลุ่ม-1 แล้วในระห่างเรียนรู้จะถูกแปลงเป็นอาเรย์แบบวันฮ็อตเพื่อใช้ตอนคำนวณเอนโทรปี
ในที่นี้สร้างให้ใช้กับการแบ่งกี่กลุ่มก็ได้ โดยให้หาจำนวนกลุ่มง่ายๆโดยดูจากค่าสูงสุด
ลองนำมาใช้จำแนกข้อมูลที่มี ๓ กลุ่มแบบนี้
np.random.seed(2)
X = np.random.normal(0,0.7,[45,2])
X[:15] += 2
X[30:,0] += 4
z = np.arange(3).repeat(15)
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='k',cmap='coolwarm')
plt.show()
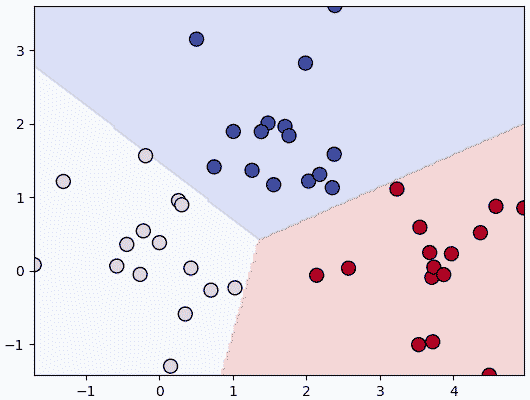
ให้โครงข่ายประสาทของเราทำการเรียนรู้แล้วทำนายแบ่งเขตพื้นที่ออกมา
prasat = Prasat(eta=0.1)
prasat.rianru(X,z,n_thamsam=250)
mx,my = np.meshgrid(np.linspace(X[:,0].min(),X[:,0].max(),200),np.linspace(X[:,1].min(),X[:,1].max(),200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = prasat.thamnai(mX).reshape(200,-1)
plt.axes(aspect=1,xlim=(X[:,0].min(),X[:,0].max()),ylim=(X[:,1].min(),X[:,1].max()))
plt.contourf(mx,my,mz,cmap='coolwarm',alpha=0.2)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='k',cmap='coolwarm')
plt.show()
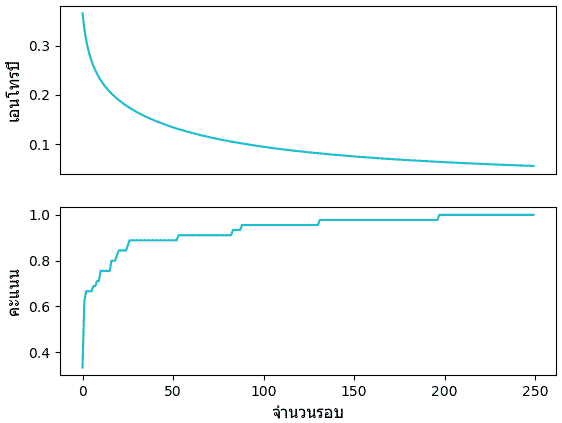
เอนโทรปีและคะแนนก็ได้บันทึกไว้ เอาออกมาดูความคืบหน้าในการเรียนรู้ได้
plt.subplot(211,xticks=[])
plt.plot(prasat.entropy,'C9')
plt.ylabel(u'เอนโทรปี',family='Tahoma',size=12)
plt.subplot(212)
plt.plot(prasat.khanaen,'C9')
plt.ylabel(u'คะแนน',family='Tahoma',size=12)
plt.xlabel(u'จำนวนรอบ',family='Tahoma',size=12)
plt.show()
สุดท้ายลองทดสอบกับข้อมูลรูปร่างต่างๆเช่นเดียวกับในบทที่ ๔ (โหลด >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar)
แต่คราวนี้เราสามารถแบ่งทุกกลุ่มได้แล้ว จึงจะใช้รูปทั้ง ๕ ชนิด

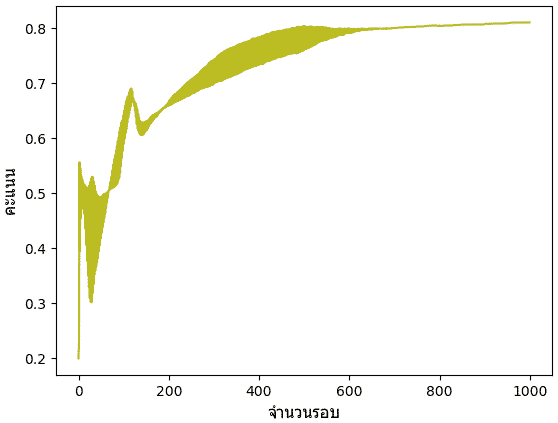
ลองให้โปรแกรมทำการเรียนรู้แล้วก็แสดงความคืบหน้าของความแม่นยำในการทำนาย
from glob import glob
d = 25
X_ = np.array([plt.imread(x) for x in sorted(glob('ruprang-raisi-25x25x1000x5/*/*.png'))])
X = X_.reshape(-1,d*d)
z = np.arange(5).repeat(1000)
prasat = Prasat(eta=0.02)
prasat.rianru(X,z,n_thamsam=1000)
print(prasat.khanaen[-1])
plt.plot(prasat.khanaen,'C8')
plt.ylabel(u'คะแนน',family='Tahoma',size=12)
plt.xlabel(u'จำนวนรอบ',family='Tahoma',size=12)
plt.show()
ดูแล้วจะเห็นว่าทายได้ถูกต้องได้แค่ 80% เท่านั้น
เพื่อจะเห็นว่าปัญหาอยู่ตรงไหนอาจลองวาดเมทริกซ์ความสับสนดู
รายละเอียดเกี่ยวกับเรื่องนี้ขอละไว้ อ่านได้ใน https://phyblas.hinaboshi.com/20170926
เขียนฟังก์ชันเมทริกซ์ความสับสน แล้วใช้ดู
def confusion_matrix(z1,z2):
n = max(z1.max(),z2.max())+1
return np.dot((z1==np.arange(n)[:,None]).astype(int),(z2[:,None]==np.arange(n)).astype(int))
print(confusion_matrix(prasat.thamnai(X),z))ดูแล้วจะเห็นว่าโปรแกรมมีปัญหาในการแยกแยะประเภทที่ 0 (วงกลม) กับประเภทที่ 2 (สี่เหลี่ยม)
[[699 10 214 18 6]
[ 33 891 149 0 61]
[265 75 605 55 0]
[ 3 10 22 927 0]
[ 0 14 10 0 933]]ที่เป็นอย่างนี้ก็เพราะโครงข่ายประสาทที่มีแค่ชั้นเดียวแบบนี้เป็นแค่การแบ่งเชิงเส้นอย่างง่าย ทำได้แค่พิจารณาง่ายๆว่ารูปแบบไหนมีการขีดที่จุดไหนมากๆ ไม่ได้คิดอะไรซับซ้อน
เพื่อที่จะพิจารณาปัญหาที่ซับซ้อนขึ้นได้จำเป็นต้องสร้างโครงข่ายที่ต่อกัน ๒ ชั้นขึ้นไป ซึ่งจะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๗
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy