โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๗: เพอร์เซปตรอนหลายชั้น
เขียนเมื่อ 2018/08/26 23:26
แก้ไขล่าสุด 2022/07/10 21:11
>> ต่อจาก บทที่ ๖
ปัญหาไม่เป็นเชิงเส้น
โครงข่ายประสาทเทียมที่มีเพียงชั้นเดียวไม่สามารถแก้ปัญหาที่ไม่เป็นเชิงเส้น (非线性, nonlinear) ได้
เช่นข้อมูลในลักษณะแบบนี้
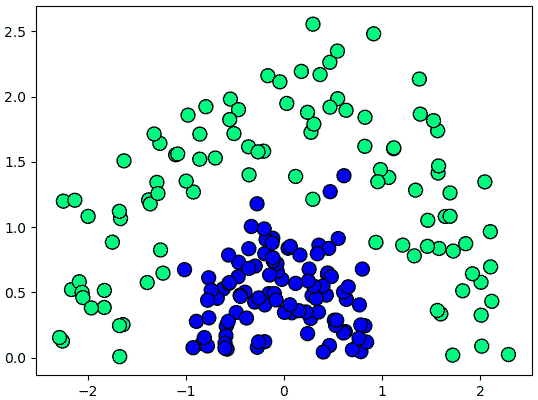
แบบนี้ไม่มีทางขีดเส้นตรงแบ่งสองกลุ่มออกจากกันได้
หรืออย่างลอจิกเกต ในบทแรกๆได้พูดถึงเกต OR และ AND ซึ่งเป็นลอจิกเกตแบบง่ายๆที่สามารถแบ่งเป็นเชิงเส้นได้
แต่คราวนี้ลองพิจารณาเกต XOR ซึ่งจะให้ค่า 1 เมื่อสัญญาณต่างกัน และให้ค่า 0 เมื่อสัญญาณเหมือนกัน
วาดภาพจะได้แบบนี้
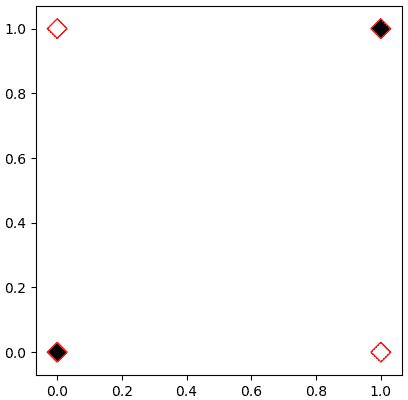
จะเห็นว่าไม่มีทางขีดเส้นตรงเส้นเดียวแบ่งจุดขาวและดำออกจากกันได้ไม่ว่ายังไงก็ตาม จึงต้องแบ่งแบบไม่เป็นเชิงเส้น
เพอร์เซปตรอนสองชั้น
เมื่อนำเซลล์ประสาทมาต่อกันเป็น ๒ ชั้นจะทำให้สามารถคำนวณแบบไม่เป็นเชิงเส้นได้
ในโครงข่ายประสาทเทียบแบบที่มีชั้นเดียวนั้นเราเอาค่า x มาคูณกับ w แล้ว บวก b จากนั้นก็ได้ค่า a แล้วนำ a ไปเข้าฟังก์ชันกระตุ้นหรือไปใช้หาคำตอบทันที
แต่เมื่อต่อเป็น ๒ ชั้น จะคำนวณในลักษณะนี้
กรณีปัญหาการจำแนกประเภท ๒ กลุ่ม
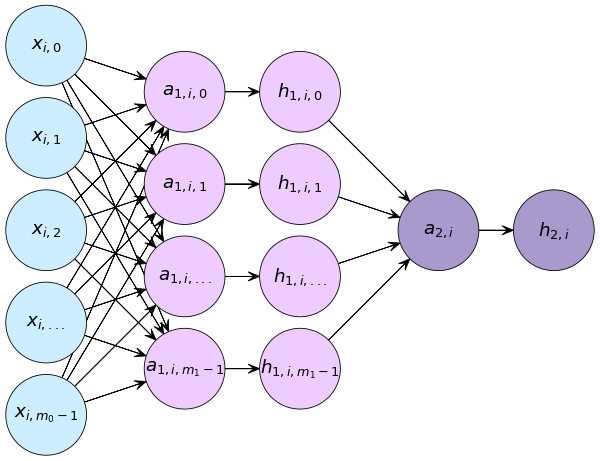
กรณีจำแนกประเภทหลายกลุ่ม
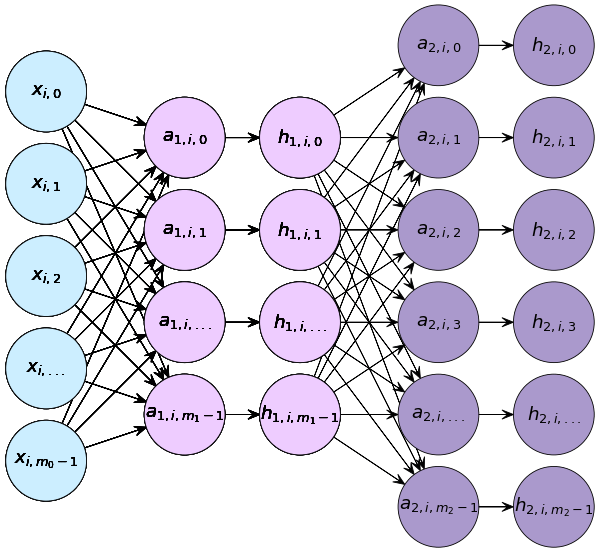
เมื่อมีการคำนวณ ๒ ชั้น แต่ละชันก็มีค่า w, b, a, h ของตัวเอง ในที่นี้เลข 1 และ 2 ที่ห้อยอยู่แสดงถึงว่าเป็นชั้นที่เท่าไหร่
แต่ละชั้นจะประกอบไปด้วยส่วนคำนวณเชิงเส้น และตามด้วยฟังก์ชันกระตุ้น ชั้นแรกมี x เป็นค่าขาเข้า และ h1 เป็นค่าขาออก ชั้นสองมี h1 เป็นค่าขาเข้าและ h2 เป็นค่าขาออก
การคำนวณในแต่ละชั้นจะเป็นแบบนี้
..(7.1)
โดยในที่นี้ ϕ หมายถึงฟังก์ชันกระตุ้น
ถ้าเป็น ๓ ชั้นก็จะเป็นแบบนี้
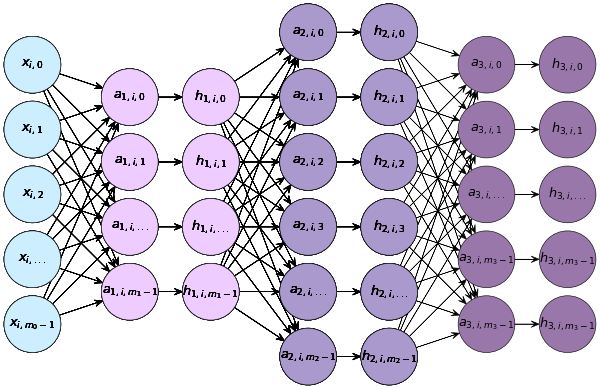
จะกี่ชั้นการคำนวณก็เป็นแบบนี้ต่อไปเรื่อยๆ
..(7.2)
ฟังก์ชันกระตุ้นระหว่างชั้น
วัตถุประสงค์ในการใส่ฟังก์ชันกระตุ้นระหว่างชั้นจะต่างจากการใส่ฟังก์ชันกระตุ้นในชั้นสุดท้าย
ฟังก์ชันกระตุ้นสำหรับชั้นสุดท้ายนั้นค่อนข้างตายตัวโดยขึ้นกับปัญหาที่วิเคราะห์ ถ้าเป็นปัญหาการจำแนกประเภทสองกลุ่มจะใช้ฟังก์ชันซิกมอยด์ แต่ถ้าเป็นจำแนกหลายกลุ่มจะใช้ฟังก์ชันซอฟต์แม็กซ์
แต่ฟังก์ชันกระตุ้นระหว่างชั้นนั้นอาจใช้ฟังก์ชันอะไรบางอย่างที่ไม่เป็นเชิงเส้น มีไว้เพื่อทำเกิดการเปลี่ยนแปลงบางอย่างที่ไม่เป็นเชิงเส้นขึ้นกับค่าในระหว่างที่ผ่านชั้น
สาเหตุที่ต้องมีฟังก์ชันกระตุ้นและต้องเป็นฟังก์ชันที่ไม่เป็นเชิงเส้นด้วยก็คือ ถ้าไม่เช่นนั้นการมีสองชั้นก็จะไม่มีความหมายอะไร
ขอยกตัวอย่าง เช่น x เป็นค่า ๒ ตัวแปร และให้ชั้นแรกให้ค่า a1 เป็น ๒ ตัวแปร ส่วนฟังก์ชันกระตุ้น ให้เป็นค่าง่ายๆคือ h1 = ca1 ส่วนชั้นสองให้เหลือ a2 เป็นตัวแปรเดียว จะได้ว่า
..(7.3)
สุดท้าย a2 ก็อยู่ในรูปของ x คูณน้ำหนักบวกไบแอส เหมือนกับตอนมีแค่ชั้นเดียว แบบนี้ยุบรวมเป็นชั้นเดียวก็มีความหมายไม่ต่างกัน
การที่มีฟังก์ชันกระตุ้นที่เป็นฟังก์ชันไม่เป็นเชิงเส้นอยู่จะทำให้ a2 ไม่อาจถูกรวบกลับมาอยู่ในรูปง่ายๆแบบนั้น จึงมีความหมาย
เดิมทีตัวเลือกที่ถูกนำมาใช้บ่อยคือฟังก์ชันซิกมอยด์ แต่ปัจจุบันที่นิยมใช้มากที่สุดคือฟังก์ชันที่มีชื่อว่า ReLU
ReLU
ReLU ย่อมาจากคำว่า Rectified Linear Unit
ฟังก์ชัน ReLU นิยามโดย
..(7.4)
เพื่อให้เห็นภาพ ลองสร้างฟังก์ชันนี้ขึ้นง่ายๆในไพธอน แล้ววาดกราฟดู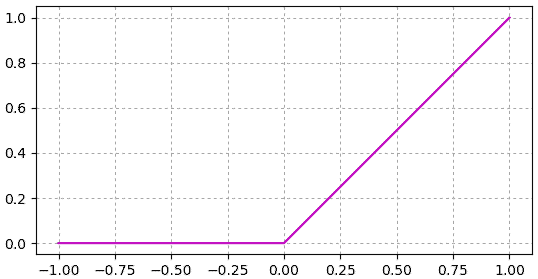
หน้าตาดูแล้วเรียบง่ายไม่มีอะไรซับซ้อนหากเทียบกับซิกมอยด์แล้ว แต่ในทางปฏิบัติใช้งานจริงหลายกรณีพบว่าใช้งานได้ดีกว่า
ฟังก์ชันนี้มีส่วนประกอบที่เป็นเชิงเส้น แต่มีการหักมุมเกิดขึ้นที่จุด 0 จึงทำให้กลายเป็นฟังก์ชันไม่เป็นเชิงเส้น และเหมาะที่จะนำมาใช้เป็นฟังก์ชันกระตุ้นระหว่างชั้นในโครงข่ายประสาทเทียม
ตัวอย่างการใช้งาน
เพื่อให้เห็นการคำนวณภายในเพอร์เซปตรอนสองชั้นอย่างง่าย จะขอยกตัวอย่างโดยใช้เกต XOR
เราอาจเขียนเพอร์เซปตรอนสองชั้นสำหรับทำเป็นเกต XOR ได้โดย
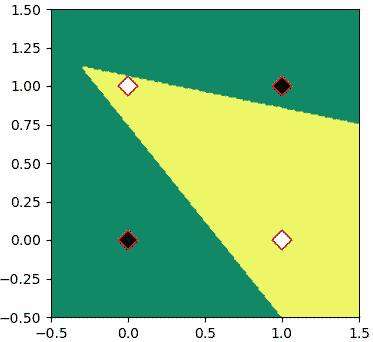
จะเห็นว่าสามารถแบ่งได้โดยเส้นแบ่งที่มีการหักมุมแบบนี้
เพื่อให้เข้าใจว่ามันทำงานยังไง ลองวาดแสดงค่าของ a1 และ h1 ดู
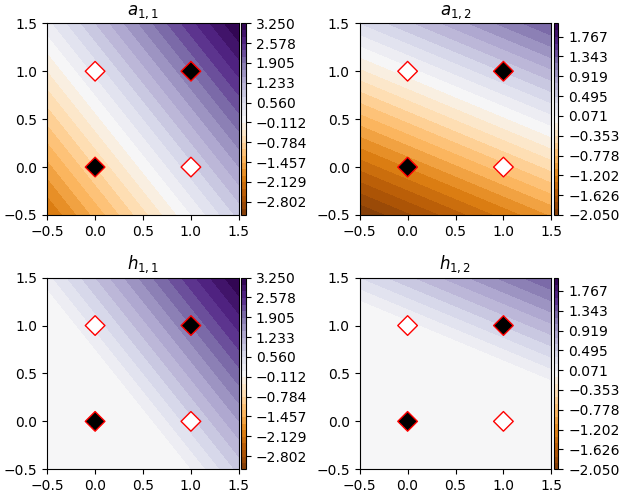
a1 ทั้งสองตัวมีค่าเป็นเชิงเส้น โดยมีแนวการผันแปรของค่าตรงกับแนวของเส้นแบ่งที่ได้
พอเป็น h1 ค่าส่วนลบก็ถูกตัดทิ้งไป รอยตัดสอดคล้องตรงกับเส้นแบ่งที่ได้
ดังนั้นเมื่อคำนวณ a2 ขึ้นจาก h1 ทั้งสองตัวนี้จึงได้ค่าที่มีจุดหักแบ่งชัดเจน
ลองแสดงค่า a2
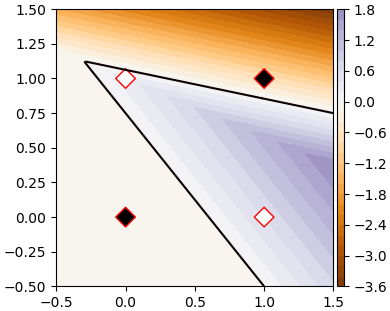
เมื่อแบ่งคำตอบตรงที่ a2=0 จึงได้ผลออกมาตามที่ต้องการ
จากตัวอย่างนี้น่าจะพอทำให้เห็นภาพว่าฟังก์ชัน ReLU ทำงานอย่างไร ทำไมการคำนวณซ้อนกันเป็นชั้นโดยมี ReLU คั่นจึงแก้ปัญหาที่ไม่ใช่เชิงเส้นได้
ในที่นี้พารามิเตอร์ทั้งสองชั้น คือ w1,b1,w1,b2 ล้วนกำหนดขึ้นเองตายตัว แต่ในการใช้งานจริงพารามิเตอร์เหล่านี้จะต้องได้มาจากการเรียนรู้จากข้อมูลตัวอย่างโดยใช้วิธีการเคลื่อนลงตามความชันและการแพร่ย้อนกลับในการปรับพารามิเตอร์
เรื่องการปรับพารามิเตอร์จะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๘
ปัญหาไม่เป็นเชิงเส้น
โครงข่ายประสาทเทียมที่มีเพียงชั้นเดียวไม่สามารถแก้ปัญหาที่ไม่เป็นเชิงเส้น (非线性, nonlinear) ได้
เช่นข้อมูลในลักษณะแบบนี้
r = np.hstack([np.random.normal(0.7,0.2,100),np.random.normal(2,0.3,100)])
t = np.random.uniform(0,np.pi,200)
X = np.array([r*np.cos(t),r*np.sin(t)]).T
z = np.array([0,1]).repeat(100)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='k',cmap='winter')
plt.show()
แบบนี้ไม่มีทางขีดเส้นตรงแบ่งสองกลุ่มออกจากกันได้
หรืออย่างลอจิกเกต ในบทแรกๆได้พูดถึงเกต OR และ AND ซึ่งเป็นลอจิกเกตแบบง่ายๆที่สามารถแบ่งเป็นเชิงเส้นได้
แต่คราวนี้ลองพิจารณาเกต XOR ซึ่งจะให้ค่า 1 เมื่อสัญญาณต่างกัน และให้ค่า 0 เมื่อสัญญาณเหมือนกัน
| x0 | x1 | z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
วาดภาพจะได้แบบนี้
X = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
z = np.array([0,1,1,0])
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='gray')
plt.show()
จะเห็นว่าไม่มีทางขีดเส้นตรงเส้นเดียวแบ่งจุดขาวและดำออกจากกันได้ไม่ว่ายังไงก็ตาม จึงต้องแบ่งแบบไม่เป็นเชิงเส้น
เพอร์เซปตรอนสองชั้น
เมื่อนำเซลล์ประสาทมาต่อกันเป็น ๒ ชั้นจะทำให้สามารถคำนวณแบบไม่เป็นเชิงเส้นได้
ในโครงข่ายประสาทเทียบแบบที่มีชั้นเดียวนั้นเราเอาค่า x มาคูณกับ w แล้ว บวก b จากนั้นก็ได้ค่า a แล้วนำ a ไปเข้าฟังก์ชันกระตุ้นหรือไปใช้หาคำตอบทันที
แต่เมื่อต่อเป็น ๒ ชั้น จะคำนวณในลักษณะนี้
กรณีปัญหาการจำแนกประเภท ๒ กลุ่ม

กรณีจำแนกประเภทหลายกลุ่ม

เมื่อมีการคำนวณ ๒ ชั้น แต่ละชันก็มีค่า w, b, a, h ของตัวเอง ในที่นี้เลข 1 และ 2 ที่ห้อยอยู่แสดงถึงว่าเป็นชั้นที่เท่าไหร่
แต่ละชั้นจะประกอบไปด้วยส่วนคำนวณเชิงเส้น และตามด้วยฟังก์ชันกระตุ้น ชั้นแรกมี x เป็นค่าขาเข้า และ h1 เป็นค่าขาออก ชั้นสองมี h1 เป็นค่าขาเข้าและ h2 เป็นค่าขาออก
การคำนวณในแต่ละชั้นจะเป็นแบบนี้
..(7.1)
โดยในที่นี้ ϕ หมายถึงฟังก์ชันกระตุ้น
ถ้าเป็น ๓ ชั้นก็จะเป็นแบบนี้

จะกี่ชั้นการคำนวณก็เป็นแบบนี้ต่อไปเรื่อยๆ
..(7.2)
ฟังก์ชันกระตุ้นระหว่างชั้น
วัตถุประสงค์ในการใส่ฟังก์ชันกระตุ้นระหว่างชั้นจะต่างจากการใส่ฟังก์ชันกระตุ้นในชั้นสุดท้าย
ฟังก์ชันกระตุ้นสำหรับชั้นสุดท้ายนั้นค่อนข้างตายตัวโดยขึ้นกับปัญหาที่วิเคราะห์ ถ้าเป็นปัญหาการจำแนกประเภทสองกลุ่มจะใช้ฟังก์ชันซิกมอยด์ แต่ถ้าเป็นจำแนกหลายกลุ่มจะใช้ฟังก์ชันซอฟต์แม็กซ์
แต่ฟังก์ชันกระตุ้นระหว่างชั้นนั้นอาจใช้ฟังก์ชันอะไรบางอย่างที่ไม่เป็นเชิงเส้น มีไว้เพื่อทำเกิดการเปลี่ยนแปลงบางอย่างที่ไม่เป็นเชิงเส้นขึ้นกับค่าในระหว่างที่ผ่านชั้น
สาเหตุที่ต้องมีฟังก์ชันกระตุ้นและต้องเป็นฟังก์ชันที่ไม่เป็นเชิงเส้นด้วยก็คือ ถ้าไม่เช่นนั้นการมีสองชั้นก็จะไม่มีความหมายอะไร
ขอยกตัวอย่าง เช่น x เป็นค่า ๒ ตัวแปร และให้ชั้นแรกให้ค่า a1 เป็น ๒ ตัวแปร ส่วนฟังก์ชันกระตุ้น ให้เป็นค่าง่ายๆคือ h1 = ca1 ส่วนชั้นสองให้เหลือ a2 เป็นตัวแปรเดียว จะได้ว่า
..(7.3)
สุดท้าย a2 ก็อยู่ในรูปของ x คูณน้ำหนักบวกไบแอส เหมือนกับตอนมีแค่ชั้นเดียว แบบนี้ยุบรวมเป็นชั้นเดียวก็มีความหมายไม่ต่างกัน
การที่มีฟังก์ชันกระตุ้นที่เป็นฟังก์ชันไม่เป็นเชิงเส้นอยู่จะทำให้ a2 ไม่อาจถูกรวบกลับมาอยู่ในรูปง่ายๆแบบนั้น จึงมีความหมาย
เดิมทีตัวเลือกที่ถูกนำมาใช้บ่อยคือฟังก์ชันซิกมอยด์ แต่ปัจจุบันที่นิยมใช้มากที่สุดคือฟังก์ชันที่มีชื่อว่า ReLU
ReLU
ReLU ย่อมาจากคำว่า Rectified Linear Unit
ฟังก์ชัน ReLU นิยามโดย
..(7.4)
เพื่อให้เห็นภาพ ลองสร้างฟังก์ชันนี้ขึ้นง่ายๆในไพธอน แล้ววาดกราฟดู
def relu(X):
return np.maximum(0,X)
x = np.linspace(-1,1,101)
plt.axes(aspect=1)
plt.plot(x,relu(x),'m')
plt.grid(ls=':')
plt.show()
หน้าตาดูแล้วเรียบง่ายไม่มีอะไรซับซ้อนหากเทียบกับซิกมอยด์แล้ว แต่ในทางปฏิบัติใช้งานจริงหลายกรณีพบว่าใช้งานได้ดีกว่า
ฟังก์ชันนี้มีส่วนประกอบที่เป็นเชิงเส้น แต่มีการหักมุมเกิดขึ้นที่จุด 0 จึงทำให้กลายเป็นฟังก์ชันไม่เป็นเชิงเส้น และเหมาะที่จะนำมาใช้เป็นฟังก์ชันกระตุ้นระหว่างชั้นในโครงข่ายประสาทเทียม
ตัวอย่างการใช้งาน
เพื่อให้เห็นการคำนวณภายในเพอร์เซปตรอนสองชั้นอย่างง่าย จะขอยกตัวอย่างโดยใช้เกต XOR
เราอาจเขียนเพอร์เซปตรอนสองชั้นสำหรับทำเป็นเกต XOR ได้โดย
w1 = np.array([[1.5,0.5],
[1.2,1.2]])
b1 = np.array([-0.8,-1.2])
w2 = np.array([1,-5])
b2 = -0.1
def p(X):
a1 = np.dot(X,w1) + b1
h1 = relu(a1)
a2 = np.dot(h1,w2) + b2
return (a2>=0).astype(int)
plt.figure(figsize=[4,4])
mx,my = np.meshgrid(np.linspace(-0.5,1.5,200),np.linspace(-0.5,1.5,200))
mX = np.array([mx,my]).T
mz = p(mX)
plt.axes(aspect=1)
plt.contourf(mx,my,mz,cmap='summer')
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='gray')
plt.show()
จะเห็นว่าสามารถแบ่งได้โดยเส้นแบ่งที่มีการหักมุมแบบนี้
เพื่อให้เข้าใจว่ามันทำงานยังไง ลองวาดแสดงค่าของ a1 และ h1 ดู
ma1 = np.dot(mX,w1) + b1
ma1 = ma1
mh1 = relu(ma1)
plt.figure(figsize=[6.4,5.2])
for i in [0,1]:
mam = np.abs(ma1[:,:,i]).max()
v = np.linspace(-mam,mam,30)
for j in [0,1]:
plt.subplot(221+i+2*j,aspect=1)
if(j):
plt.title('$h_{1,%d}$'%(i+1))
plt.contourf(mx,my,mh1[:,:,i],v,cmap='PuOr')
else:
plt.title('$a_{1,%d}$'%(i+1))
plt.contourf(mx,my,ma1[:,:,i],v,cmap='PuOr')
plt.colorbar(pad=0.01,aspect=40)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='gray')
plt.tight_layout()
plt.show()
a1 ทั้งสองตัวมีค่าเป็นเชิงเส้น โดยมีแนวการผันแปรของค่าตรงกับแนวของเส้นแบ่งที่ได้
พอเป็น h1 ค่าส่วนลบก็ถูกตัดทิ้งไป รอยตัดสอดคล้องตรงกับเส้นแบ่งที่ได้
ดังนั้นเมื่อคำนวณ a2 ขึ้นจาก h1 ทั้งสองตัวนี้จึงได้ค่าที่มีจุดหักแบ่งชัดเจน
ลองแสดงค่า a2
ma2 = np.dot(mh1,w2) + b2
plt.figure(figsize=[4.4,3.6])
plt.axes(aspect=1)
mam = np.abs(ma2).max()
plt.contour(mx,my,ma2,[0],cmap='hot')
plt.contourf(mx,my,ma2,30,cmap='PuOr',vmin=-mam,vmax=mam)
plt.colorbar(pad=0.01,aspect=40)
plt.scatter(X[:,0],X[:,1],100,c=z,edgecolor='r',marker='D',cmap='gray')
plt.show()
เมื่อแบ่งคำตอบตรงที่ a2=0 จึงได้ผลออกมาตามที่ต้องการ
จากตัวอย่างนี้น่าจะพอทำให้เห็นภาพว่าฟังก์ชัน ReLU ทำงานอย่างไร ทำไมการคำนวณซ้อนกันเป็นชั้นโดยมี ReLU คั่นจึงแก้ปัญหาที่ไม่ใช่เชิงเส้นได้
ในที่นี้พารามิเตอร์ทั้งสองชั้น คือ w1,b1,w1,b2 ล้วนกำหนดขึ้นเองตายตัว แต่ในการใช้งานจริงพารามิเตอร์เหล่านี้จะต้องได้มาจากการเรียนรู้จากข้อมูลตัวอย่างโดยใช้วิธีการเคลื่อนลงตามความชันและการแพร่ย้อนกลับในการปรับพารามิเตอร์
เรื่องการปรับพารามิเตอร์จะพูดถึงในบทต่อไป
>> อ่านต่อ บทที่ ๘
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy