โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๘: การเรียนรู้ของเพอร์เซปตรอนหลายชั้น
เขียนเมื่อ 2018/08/26 23:27
แก้ไขล่าสุด 2022/07/10 21:10
>> ต่อจาก บทที่ ๗
ในบทนี้จะสร้างเพอร์เซปตรอนสองชั้นเพื่อแก้ปัญหาการจำแนกประเภท
การคำนวณ
พิจารณาปัญหาการจำแนกประเภทหลายกลุ่มโดยใช้เพอร์เซปตรอนสองชั้นโดยมีฟังก์ชันกระตุ้นระหว่างชั้นเป็นฟังก์ชันซิกมอยด์ (ที่จริง ReLU นิยมใช้มากกว่า แต่เพื่อความง่ายในที่นี้จะใช้ซิกมอยด์ ถ้าเข้าใจหลักการแล้วจะเปลี่ยนมาใช้ ReLU แทนก็ทำได้ทันที)
หลักการคิดก็จะใช้การแพร่ย้อนกลับเพื่อคำนวณหาอนุพันธ์ แล้วสุดท้ายก็ใช้การเคลื่อนลงตามความชันเพื่อปรับพารามิเตอร์ เช่นเดียวกับในบทก่อนๆ
เริ่มจากเขียนกราฟคำนวณ
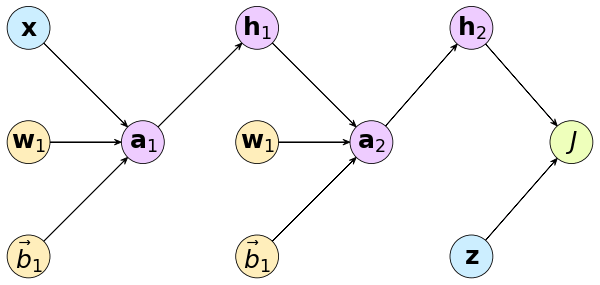
โดย
..(8.1)
หาอนุพันธ์ได้
..(8.2)
แทนลงกราฟคำนวณได้แบบนี้
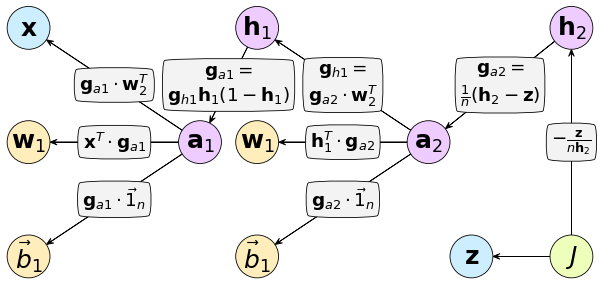
พารามิเตอร์ที่ต้องปรับมีทั้งหมด ๔ ตัว
..(8.3)
ส่วนค่าน้ำหนักตั้งต้นในที่นี้จะกำหนดแบบสุ่ม เพราะในเพอร์เซปตรอนสองชั้นขึ้นไปปกติแล้วค่าน้ำหนักตั้งต้นจะกำหนดเป็น 0 หมดไม่ได้ เหตุผลจะกล่าวถึงโดยละเอียดอีกทีในบทที่ ๑๓ ส่วนค่าไบแอสยังคงกำหนดเป็น 0
โปรแกรม
คราวนี้ลองยกตัวอย่างเป็นข้อมูล ๔ กลุ่มที่ไม่อาจจำแนกโดยเชิงเส้นได้แบบนี้
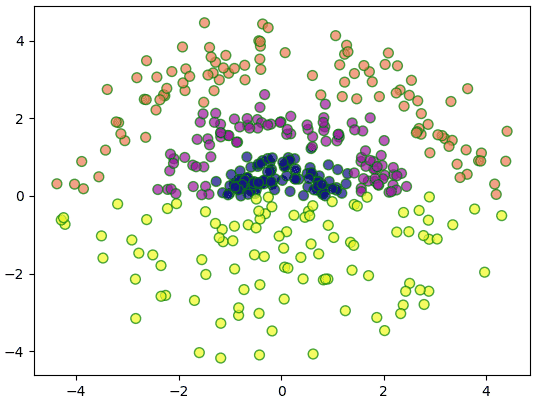
สร้างคลาสขึ้นมาแล้วใช้จำแนกกลุ่ม
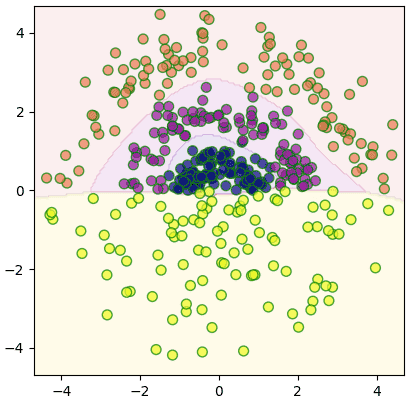
สามารถแบ่งออกมาได้อย่างสวยงาม
จำนวนเซลล์ประสาทในชั้นตรงกลางตั้งไว้ให้สามารถปรับได้ตามที่ต้องการ อาจลองปรับดูแล้วเทียบผลลัพธ์ได้
โดยทั่วไปแล้วจำนวนเซลล์ในชั้นซ่อนเป็นอะไรที่ไม่ตายตัว ยากจะอธิบาย หากให้เยอะๆไว้ก็คิดอะไรได้ซับซ้อนขึ้น แต่ก็มีแนวโน้มที่จะเกิดการเรียนรู้เกินจากการที่มิติเยอะเกินไป จึงไม่ใช่ว่ายิ่งเพิ่มก็ยิ่งดี
ต่อมาลองใช้กับข้อมูลรูปร่างแบบเดียวกับที่ใช้ในบทที่ ๖ (โหลด >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar)
โค้ดจะใช้เวลาค่อนข้างนานเพราะข้อมูลเยอะ ที่จริงแล้วสามารถทำให้เร็วขึ้นได้โดยใช้การเคลื่อนลงตามความชันแบบปรับปรุงใหม่ (บทที่ ๑๒) และมินิแบตช์ (บทที่ ๑๕) แต่ตอนนี้ยังไม่ได้กล่าวถึงจึงทำแบบนี้ไปก่อน
จะเห็นว่าถ้าเข้าใจหลักการแล้วจะโครงจ่ายสองชั้นหรือหลายชั้นขึ้นไปอีกก็ไม่ยาก รูปแบบการคำนวณก็ซ้ำเดิม ต่อไปเรื่อยๆ
แต่ว่าเขียนอะไรคล้ายเดิมซ้ำๆแบบนี้ไปเรื่อยๆก็ดูยืดยาว ในเมื่อเรารู้ว่าโครงสร้างของโครงข่ายแบ่งเป็นชั้นๆแน่นอน แล้วแต่ละชั้นก็มีการคำนวณที่แน่นอนแบบนี้ ถ้างั้นก็สร้างเป็นชั้นๆแล้วค่อยเอามาประกอบน่าจะเป็นวิธีที่มีประสิทธิภาพมากกว่า
ในเฟรมเวิร์กโครงข่ายประสาทเทียมเช่น pytorch หรือ keras ล้วนใช้วิธีการนิยามคลาสของชั้นต่างๆไว้แล้วเวลาใช้ก็นำมาประกอบ
ดังนั้นในบทต่อไปจะแนะนำวิธีการสร้างโครงสร้างเป็นชั้นๆ
>> อ่านต่อ บทที่ ๙
ในบทนี้จะสร้างเพอร์เซปตรอนสองชั้นเพื่อแก้ปัญหาการจำแนกประเภท
การคำนวณ
พิจารณาปัญหาการจำแนกประเภทหลายกลุ่มโดยใช้เพอร์เซปตรอนสองชั้นโดยมีฟังก์ชันกระตุ้นระหว่างชั้นเป็นฟังก์ชันซิกมอยด์ (ที่จริง ReLU นิยมใช้มากกว่า แต่เพื่อความง่ายในที่นี้จะใช้ซิกมอยด์ ถ้าเข้าใจหลักการแล้วจะเปลี่ยนมาใช้ ReLU แทนก็ทำได้ทันที)
หลักการคิดก็จะใช้การแพร่ย้อนกลับเพื่อคำนวณหาอนุพันธ์ แล้วสุดท้ายก็ใช้การเคลื่อนลงตามความชันเพื่อปรับพารามิเตอร์ เช่นเดียวกับในบทก่อนๆ
เริ่มจากเขียนกราฟคำนวณ

โดย
..(8.1)
หาอนุพันธ์ได้
..(8.2)
แทนลงกราฟคำนวณได้แบบนี้

พารามิเตอร์ที่ต้องปรับมีทั้งหมด ๔ ตัว
..(8.3)
ส่วนค่าน้ำหนักตั้งต้นในที่นี้จะกำหนดแบบสุ่ม เพราะในเพอร์เซปตรอนสองชั้นขึ้นไปปกติแล้วค่าน้ำหนักตั้งต้นจะกำหนดเป็น 0 หมดไม่ได้ เหตุผลจะกล่าวถึงโดยละเอียดอีกทีในบทที่ ๑๓ ส่วนค่าไบแอสยังคงกำหนดเป็น 0
โปรแกรม
คราวนี้ลองยกตัวอย่างเป็นข้อมูล ๔ กลุ่มที่ไม่อาจจำแนกโดยเชิงเส้นได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(4)
r = np.hstack([np.random.normal(0.8,0.25,100),
np.random.normal(2,0.3,100),
np.random.normal(3.6,0.4,100),
np.random.uniform(0.2,4.5,100)])
t = np.hstack([np.random.uniform(0,np.pi,300),
np.random.uniform(-np.pi,0,100)])
X = np.array([r*np.cos(t),r*np.sin(t)]).T
z = np.arange(4).repeat(100)
plt.scatter(X[:,0],X[:,1],50,c=z,alpha=0.7,edgecolor='g',cmap='plasma')
plt.show()
สร้างคลาสขึ้นมาแล้วใช้จำแนกกลุ่ม
def sigmoid(x):
return 1/(1+np.exp(-x))
def softmax(x):
exp_x = np.exp(x.T-x.max(1))
return (exp_x/exp_x.sum(0)).T
def ha_1h(z,n):
return (z[:,None]==range(n)).astype(int)
def ha_entropy(z,h):
return -(np.log(h[z==1]+1e-10)).mean()
class Prasat2chan:
def __init__(self,m,eta):
self.m = m
self.eta = eta
def rianru(self,X,z,n_thamsam):
self.kiklum = int(z.max()+1)
Z = ha_1h(z,self.kiklum)
self.w1 = np.random.normal(0,1,[X.shape[1],self.m])
self.b1 = np.zeros(self.m)
self.w2 = np.random.normal(0,1,[self.m,self.kiklum])
self.b2 = np.zeros(self.kiklum)
self.entropy = []
self.khanaen = []
for o in range(n_thamsam):
a1 = self.ha_a1(X)
h1 = sigmoid(a1)
a2 = self.ha_a2(h1)
h2 = softmax(a2)
J = ha_entropy(Z,h2)
ga2 = (h2-Z)/len(Z)
gh1 = np.dot(ga2,self.w2.T)
ga1 = gh1*h1*(1-h1)
self.w2 -= self.eta*np.dot(h1.T,ga2)
self.b2 -= self.eta*ga2.sum(0)
self.w1 -= self.eta*np.dot(X.T,ga1)
self.b1 -= self.eta*ga1.sum(0)
self.entropy.append(J)
khanaen = ((a2).argmax(1)==z).mean()
self.khanaen.append(khanaen)
if(o%100==99):
print(u'ผ่านไป %d รอบ คะแนน %.3f'%(o+1,khanaen))
def thamnai(self,X):
a1 = self.ha_a1(X)
h1 = sigmoid(a1)
a2 = self.ha_a2(h1)
h2 = softmax(a2)
return h2.argmax(1)
def ha_a1(self,X):
return np.dot(X,self.w1) + self.b1
def ha_a2(self,X):
return np.dot(X,self.w2) + self.b2
prasat = Prasat2chan(m=10,eta=0.5)
prasat.rianru(X,z,n_thamsam=2000)
mm = X.max()*1.05
mx,my = np.meshgrid(np.linspace(-mm,mm,200),np.linspace(-mm,mm,200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = prasat.thamnai(mX).reshape(200,-1)
plt.axes(aspect=1,xlim=(-mm,mm),ylim=(-mm,mm))
plt.contourf(mx,my,mz,cmap='plasma',alpha=0.1)
plt.scatter(X[:,0],X[:,1],50,c=z,alpha=0.7,edgecolor='g',cmap='plasma')
plt.show()
สามารถแบ่งออกมาได้อย่างสวยงาม
จำนวนเซลล์ประสาทในชั้นตรงกลางตั้งไว้ให้สามารถปรับได้ตามที่ต้องการ อาจลองปรับดูแล้วเทียบผลลัพธ์ได้
โดยทั่วไปแล้วจำนวนเซลล์ในชั้นซ่อนเป็นอะไรที่ไม่ตายตัว ยากจะอธิบาย หากให้เยอะๆไว้ก็คิดอะไรได้ซับซ้อนขึ้น แต่ก็มีแนวโน้มที่จะเกิดการเรียนรู้เกินจากการที่มิติเยอะเกินไป จึงไม่ใช่ว่ายิ่งเพิ่มก็ยิ่งดี
ต่อมาลองใช้กับข้อมูลรูปร่างแบบเดียวกับที่ใช้ในบทที่ ๖ (โหลด >> https://phyblas.hinaboshi.com/triamhai/ruprang-raisi-25x25x1000x5.rar)
from glob import glob
n = 1000
X = np.array([plt.imread(x) for x in sorted(glob('ruprang-raisi-25x25x1000x5/*/*.png'))])
X = X.reshape(-1,25*25)
z = np.arange(5).repeat(n)
prasat = Prasat2chan(m=50,eta=0.25)
prasat.rianru(X,z,n_thamsam=12000)
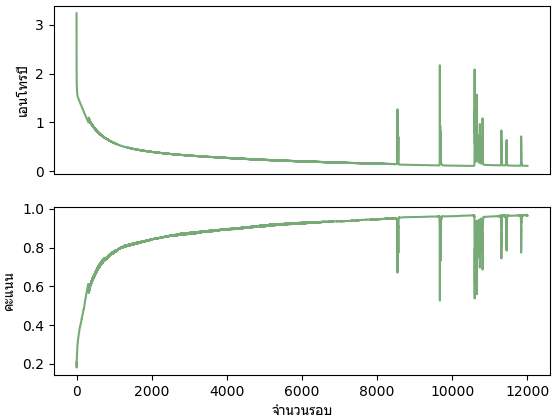
plt.subplot(211,xticks=[])
plt.plot(prasat.entropy,'#77aa77')
plt.ylabel(u'เอนโทรปี',family='Tahoma')
plt.subplot(212)
plt.plot(prasat.khanaen,'#77aa77')
plt.ylabel(u'คะแนน',family='Tahoma')
plt.xlabel(u'จำนวนรอบ',family='Tahoma')
print(prasat.khanaen[-1])
plt.show()โค้ดจะใช้เวลาค่อนข้างนานเพราะข้อมูลเยอะ ที่จริงแล้วสามารถทำให้เร็วขึ้นได้โดยใช้การเคลื่อนลงตามความชันแบบปรับปรุงใหม่ (บทที่ ๑๒) และมินิแบตช์ (บทที่ ๑๕) แต่ตอนนี้ยังไม่ได้กล่าวถึงจึงทำแบบนี้ไปก่อน

จะเห็นว่าถ้าเข้าใจหลักการแล้วจะโครงจ่ายสองชั้นหรือหลายชั้นขึ้นไปอีกก็ไม่ยาก รูปแบบการคำนวณก็ซ้ำเดิม ต่อไปเรื่อยๆ
แต่ว่าเขียนอะไรคล้ายเดิมซ้ำๆแบบนี้ไปเรื่อยๆก็ดูยืดยาว ในเมื่อเรารู้ว่าโครงสร้างของโครงข่ายแบ่งเป็นชั้นๆแน่นอน แล้วแต่ละชั้นก็มีการคำนวณที่แน่นอนแบบนี้ ถ้างั้นก็สร้างเป็นชั้นๆแล้วค่อยเอามาประกอบน่าจะเป็นวิธีที่มีประสิทธิภาพมากกว่า
ในเฟรมเวิร์กโครงข่ายประสาทเทียมเช่น pytorch หรือ keras ล้วนใช้วิธีการนิยามคลาสของชั้นต่างๆไว้แล้วเวลาใช้ก็นำมาประกอบ
ดังนั้นในบทต่อไปจะแนะนำวิธีการสร้างโครงสร้างเป็นชั้นๆ
>> อ่านต่อ บทที่ ๙
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy