โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๙: การสร้างชั้นคำนวณไปข้างหน้าและแพร่ย้อนกลับ
เขียนเมื่อ 2018/08/26 23:28
แก้ไขล่าสุด 2021/09/28 16:42
>> ต่อจาก บทที่ ๘
โครงข่ายประสาทเทียมที่ดูแล้วลึกล้ำ ล้วนประกอบขึ้นมาจากชิ้นส่วนที่แบ่งเป็นชั้นต่างๆ
แต่ละชั้นมีการคำนวณไปข้างหน้าตามลำดับแล้วสุดท้ายก็คำนวณแพร่ย้อนกลับเพื่อหาอนุพันธ์
ในบทนี้จะมาลองสร้างโครงสร้างแบบนั้น
ชั้นของตัวดำเนินการพื้นฐาน
ก่อนอื่นพิจารณาการคำนวณของตัวดำเนินการง่ายๆ เช่น บวก ลบ คูณ หาร ซึ่งหาอนุพันธ์ได้ดังนี้
..(9.1)
ลองสร้างคลาสของชั้นต่างๆที่มีเมธอดการคำนวณไปข้างหน้าและย้อนกลับ ดังนี้
เวลาที่คำนวณไปข้างหน้าเพื่อคำนวณค่าจะใช้เมธอด .pai() ส่วนเวลาคำนวณย้อนกลับเพื่อหาอนุพันธ์ .yon()
เวลาคำนวณไปข้างหน้าก็คือรับเอาตัวแปรมาดำเนินการ คือบวกลบคูณหารกัน โดยระหว่างนั้นจะมีการเก็บค่าที่จะต้องใช้ตอนหาอนุพันธ์ตอนคำนวณแพร่ย้อนกลับไว้ด้วย
ส่วนเวลาคำนวณย้อนกลับจะรับค่าอนุพันธ์ที่สะสมจากชั้นก่อนแล้วคูณเพิ่มค่าในชั้นนั้นเข้าไปตามกฎลูกโซ่
ยกตัวอย่างเช่นสมการคำนวณง่ายๆแบบนี้
..(9.2)
หากเขียนกราฟคำนวณจะได้
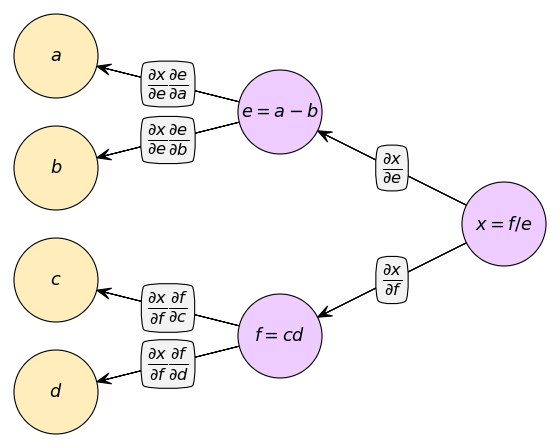
จากสมการตัวอย่าง ให้ a=1,b=2,c=3,d=4 ถ้าใช้ชั้นต่างๆเหล่านี้คำนวณจะทำได้ดังนี้
ได้
g ในที่นี้แทนอนุพันธ์ของ x เทียบกับตัวแปรตัวนั้น
ลองคำนวณด้วยตัวเองเทียบคำตอบดูได้
เช่นเดียวกัน ชั้นของฟังก์ชันเอกซ์โพเนนเชียลและลอการิธึมก็อาจเขียนได้ดังนี้
ชั้นของฟังก์ชันกระตุ้น
ชั้นของฟังก์ชันซิกมอยด์และ ReLU อาจสร้างได้ดังนี้
สำหรับ ReLU นั้นอาจเข้าใจยากเล็กน้อย หลักการก็คือต้องสร้างตัวกรองบันทึกไว้ว่าตอนที่คำนวณไปข้างหน้านั้นมีค่าไหนบ้างที่เป็นบวก จากนั้นตอนแพร่ย้อนก็กรองให้ค่าอนุพันธ์แพร่ไปต่อได้เฉพาะส่วนนั้น ที่เหลือเป็น 0
ชั้นที่มีพารามิเตอร์
ฟังก์ชันที่แนะนำมาก่อนหน้านี้เป็นฟังก์ชันที่ไม่มีพารามิเตอร์ที่ปรับค่าได้ จะคำนวณกี่ทีก็ให้ผลเหมือนเดิมตลอด
แต่สำหรับในโครงข่ายประสาทเทียมแล้ว ชั้นที่สำคัญที่สุดก็คือชั้นผลคูณเชิงเส้น ซึ่งเป็นชั้นที่มีพารามิเตอร์ค่าน้ำหนัก w และไบแอส b
สำหรับชั้นที่มีพารามิเตอร์นั้น ระหว่างคำนวณย้อนกลับเราจะให้เก็บค่าอนุพันธ์เอาไว้ จากนั้นตอนหลังจึงจะใช้ค่านี้เพื่อกำหนดว่าจะปรับค่ายังไง
ยกตัวอย่างฟังก์ชันง่ายๆสำหรับตัวแปรเดี่ยวที่แค่คูณ w ตัวเดียวแล้วบวก b จะสร้างได้แบบนี้
ค่าอนุพันธ์จะเป็น 0 ตอนเริ่ม แล้วพอมีการแพร่ย้อนกลับจึงบวกเพิ่ม ถ้าใช้เสร็จแล้วควรจะต้องล้างให้กลับมาเป็น 0 อีกก่อนการคำนวณครั้งต่อไป ไม่เช่นนั้นของเก่าจะถูกบวกเพิ่มสะสมไป
ที่ต้องให้เริ่มจาก 0 แล้วบวกเพิ่มแทนที่จะให้แทนเป็นค่านั้นเลยก็เพราะถ้าการคำนวณมีการแตกสายไปอนุพันธ์อาจต้องคำนวณแยกสายแล้วบวกกัน
ตัวอย่างการใช้
ต่อมาจะนิยามชั้นที่ใช้ในโครงข่ายประสาทเทียมจริงๆ คือเป็นชั้นที่มีการคูณแบบเมทริกซ์
โดยทั่วไปแล้วชั้นคำนวณเชิงเส้นแบบนี้มีชื่อเรียกว่า affine layer ดังนั้นในที่นี้ก็จะขอใช้ชื่อคลาสว่า Affin
คำนี้มาจากภาษาละตินว่า affinis มีความหมายว่า "เกี่ยวพันเชื่อมต่อกัน" ในภาษาไทยมีการแปลคำว่า affine เป็น "สัมพรรค"
นอกจากนี้ยังมีชื่อเรียกว่าชั้น Linear ถ้าเป็นใน pytorch หรือ chainer ก็ใช้ชื่อนี้ ส่วนใน keras จะใช้ชื่อว่า Dense
อาจนิยามชั้นขึ้นมาได้ดังนี้
นำหนัก w และ b จะกำหนดตอนสร้างออบเจ็กต์ โดยขนาดต้องสัมพันธ์กับการคำนวณที่ต้องการ w เป็นอาเรย์สองมิติ ขนาดเท่ากับ (ขนาดค่าป้อนเข้า,ขนาดค่าขาออก) ส่วน b เป็นอาเรย์หนึ่งมิติ ขนาดเท่ากับค่าขาออก
ตัวอย่างการใช้
สำหรับการนำมาใช้งานจริงเพื่อสร้างโครงข่ายประสาทเทียมจะอยู่ในบทต่อไป
>> อ่านต่อ บทที่ ๑๐
โครงข่ายประสาทเทียมที่ดูแล้วลึกล้ำ ล้วนประกอบขึ้นมาจากชิ้นส่วนที่แบ่งเป็นชั้นต่างๆ
แต่ละชั้นมีการคำนวณไปข้างหน้าตามลำดับแล้วสุดท้ายก็คำนวณแพร่ย้อนกลับเพื่อหาอนุพันธ์
ในบทนี้จะมาลองสร้างโครงสร้างแบบนั้น
ชั้นของตัวดำเนินการพื้นฐาน
ก่อนอื่นพิจารณาการคำนวณของตัวดำเนินการง่ายๆ เช่น บวก ลบ คูณ หาร ซึ่งหาอนุพันธ์ได้ดังนี้
..(9.1)
ลองสร้างคลาสของชั้นต่างๆที่มีเมธอดการคำนวณไปข้างหน้าและย้อนกลับ ดังนี้
class Buak:
def pai(self,x,y): # ไปข้างหน้า
return x+y
def yon(self,g): # ย้อนกลับ
return g, g
class Lop:
def pai(self,x,y):
return x-y
def yon(self,g):
return g, -g
class Khun:
def pai(self,x,y):
self.x = x
self.y = y
return x*y
def yon(self,g):
return g*self.y, g*self.x
class Han:
def pai(self,x,y):
self.x = x
self.y = y
return x/y
def yon(self,g):
return g/self.y, -g*self.x/self.y**2เวลาที่คำนวณไปข้างหน้าเพื่อคำนวณค่าจะใช้เมธอด .pai() ส่วนเวลาคำนวณย้อนกลับเพื่อหาอนุพันธ์ .yon()
เวลาคำนวณไปข้างหน้าก็คือรับเอาตัวแปรมาดำเนินการ คือบวกลบคูณหารกัน โดยระหว่างนั้นจะมีการเก็บค่าที่จะต้องใช้ตอนหาอนุพันธ์ตอนคำนวณแพร่ย้อนกลับไว้ด้วย
ส่วนเวลาคำนวณย้อนกลับจะรับค่าอนุพันธ์ที่สะสมจากชั้นก่อนแล้วคูณเพิ่มค่าในชั้นนั้นเข้าไปตามกฎลูกโซ่
ยกตัวอย่างเช่นสมการคำนวณง่ายๆแบบนี้
..(9.2)
หากเขียนกราฟคำนวณจะได้

จากสมการตัวอย่าง ให้ a=1,b=2,c=3,d=4 ถ้าใช้ชั้นต่างๆเหล่านี้คำนวณจะทำได้ดังนี้
lop = Lop()
khun = Khun()
han = Han()
a = 1
b = 2
c = 3
d = 4
e = lop.pai(a,b)
f = khun.pai(c,d)
x = han.pai(f,e)
print('e=%d, f=%d, x=%d'%(e,f,x))
gf,ge = han.yon(1)
gc,gd = khun.yon(gf)
ga,gb = lop.yon(ge)
print('ga=%d, gb=%d, gc=%d\ngd=%d, ge=%d, gf=%d'%(ga,gb,gc,gd,gf,ge))ได้
e=-1, f=12, x=-12
ga=-12, gb=12, gc=-4
gd=-3, ge=-1, gf=-12g ในที่นี้แทนอนุพันธ์ของ x เทียบกับตัวแปรตัวนั้น
ลองคำนวณด้วยตัวเองเทียบคำตอบดูได้
เช่นเดียวกัน ชั้นของฟังก์ชันเอกซ์โพเนนเชียลและลอการิธึมก็อาจเขียนได้ดังนี้
import numpy as np
class Exp:
def pai(self,x):
self.expx = np.exp(x)
return self.expx
def yon(self,g):
return g*self.expx
class Ln:
def pai(self,x):
self.x = x
return np.log(x)
def yon(self,g):
return g/self.xชั้นของฟังก์ชันกระตุ้น
ชั้นของฟังก์ชันซิกมอยด์และ ReLU อาจสร้างได้ดังนี้
class Sigmoid:
def pai(self,x):
self.h = 1/(1+np.exp(-x))
return self.h
def yon(self,g):
return g*(1.-self.h)*self.h
class Relu:
def pai(self,x):
self.krong = (x>0)
return np.where(self.krong,x,0)
def yon(self,g):
return np.where(self.krong,g,0)สำหรับ ReLU นั้นอาจเข้าใจยากเล็กน้อย หลักการก็คือต้องสร้างตัวกรองบันทึกไว้ว่าตอนที่คำนวณไปข้างหน้านั้นมีค่าไหนบ้างที่เป็นบวก จากนั้นตอนแพร่ย้อนก็กรองให้ค่าอนุพันธ์แพร่ไปต่อได้เฉพาะส่วนนั้น ที่เหลือเป็น 0
ชั้นที่มีพารามิเตอร์
ฟังก์ชันที่แนะนำมาก่อนหน้านี้เป็นฟังก์ชันที่ไม่มีพารามิเตอร์ที่ปรับค่าได้ จะคำนวณกี่ทีก็ให้ผลเหมือนเดิมตลอด
แต่สำหรับในโครงข่ายประสาทเทียมแล้ว ชั้นที่สำคัญที่สุดก็คือชั้นผลคูณเชิงเส้น ซึ่งเป็นชั้นที่มีพารามิเตอร์ค่าน้ำหนัก w และไบแอส b
สำหรับชั้นที่มีพารามิเตอร์นั้น ระหว่างคำนวณย้อนกลับเราจะให้เก็บค่าอนุพันธ์เอาไว้ จากนั้นตอนหลังจึงจะใช้ค่านี้เพื่อกำหนดว่าจะปรับค่ายังไง
ยกตัวอย่างฟังก์ชันง่ายๆสำหรับตัวแปรเดี่ยวที่แค่คูณ w ตัวเดียวแล้วบวก b จะสร้างได้แบบนี้
class KhunW_BuakB:
def __init__(self,w,b):
self.w = w
self.b = b
self.gw = 0
self.gb = 0
def pai(self,x):
self.x = x
return self.w*x+self.b
def yon(self,g):
self.gw += g*self.x
self.gb += g
return g*self.wค่าอนุพันธ์จะเป็น 0 ตอนเริ่ม แล้วพอมีการแพร่ย้อนกลับจึงบวกเพิ่ม ถ้าใช้เสร็จแล้วควรจะต้องล้างให้กลับมาเป็น 0 อีกก่อนการคำนวณครั้งต่อไป ไม่เช่นนั้นของเก่าจะถูกบวกเพิ่มสะสมไป
ที่ต้องให้เริ่มจาก 0 แล้วบวกเพิ่มแทนที่จะให้แทนเป็นค่านั้นเลยก็เพราะถ้าการคำนวณมีการแตกสายไปอนุพันธ์อาจต้องคำนวณแยกสายแล้วบวกกัน
ตัวอย่างการใช้
f1 = KhunW_BuakB(2,1)
f2 = KhunW_BuakB(3,4)
x = 3
y = f1.pai(x)
print(y) # 3*2+1 = 7
z = f2.pai(y)
print(z) # 7*3+4 = 25
gy = f2.yon(1)
print(gy) # 1*3 = 3
print(f2.gw,f2.gb) # 1*7 = 7, 1
gx = f1.yon(gy)
print(gx) # 3*2 = 6
print(f1.gw,f1.gb) # 3*3 = 9, 3ต่อมาจะนิยามชั้นที่ใช้ในโครงข่ายประสาทเทียมจริงๆ คือเป็นชั้นที่มีการคูณแบบเมทริกซ์
โดยทั่วไปแล้วชั้นคำนวณเชิงเส้นแบบนี้มีชื่อเรียกว่า affine layer ดังนั้นในที่นี้ก็จะขอใช้ชื่อคลาสว่า Affin
คำนี้มาจากภาษาละตินว่า affinis มีความหมายว่า "เกี่ยวพันเชื่อมต่อกัน" ในภาษาไทยมีการแปลคำว่า affine เป็น "สัมพรรค"
นอกจากนี้ยังมีชื่อเรียกว่าชั้น Linear ถ้าเป็นใน pytorch หรือ chainer ก็ใช้ชื่อนี้ ส่วนใน keras จะใช้ชื่อว่า Dense
อาจนิยามชั้นขึ้นมาได้ดังนี้
class Affin:
def __init__(self,w,b):
self.w = w
self.b = b
self.gw = 0
self.gb = 0
def pai(self,X):
self.X = X
return np.dot(X,self.w) + self.b
def yon(self,g):
self.gw += np.dot(self.X.T,g)
self.gb += g.sum(0)
return np.dot(g,self.w.T)นำหนัก w และ b จะกำหนดตอนสร้างออบเจ็กต์ โดยขนาดต้องสัมพันธ์กับการคำนวณที่ต้องการ w เป็นอาเรย์สองมิติ ขนาดเท่ากับ (ขนาดค่าป้อนเข้า,ขนาดค่าขาออก) ส่วน b เป็นอาเรย์หนึ่งมิติ ขนาดเท่ากับค่าขาออก
ตัวอย่างการใช้
af = Affin(np.random.randint(0,9,[3,4]),np.random.randint(0,9,4))
x = np.random.randint(0,9,[2,3])
print(x)
print(af.w)
print(af.b)
a = af.pai(x)
print(a)
gx = af.yon(np.ones([2,4]))
print(gx)
print(af.gw)
print(af.gb)[[3 1 3]
[1 3 3]]
[[8 0 8 8]
[0 7 0 8]
[8 1 6 5]]
[7 3 5 2]
[[55 13 47 49]
[39 27 31 49]]
[[ 24. 15. 20.]
[ 24. 15. 20.]]
[[ 4. 4. 4. 4.]
[ 4. 4. 4. 4.]
[ 6. 6. 6. 6.]]
[ 2. 2. 2. 2.]สำหรับการนำมาใช้งานจริงเพื่อสร้างโครงข่ายประสาทเทียมจะอยู่ในบทต่อไป
>> อ่านต่อ บทที่ ๑๐
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy