โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑๓: การกำหนดค่าพารามิเตอร์ตั้งต้น
เขียนเมื่อ 2018/08/26 23:32
แก้ไขล่าสุด 2021/09/28 16:42
>> ต่อจาก บทที่ ๑๒
ทำไมจึงไม่กำหนดค่าน้ำหนักเป็น 0
ตั้งแต่บทที่ ๘ นั้นเราได้เริ่มกำหนดค่าพารามิเตอร์น้ำหนัก w ตั้งต้นให้แจกแจงแบบเกาส์
สาเหตุที่ไม่กำหนดให้เป็น 0 ทั้งหมดเหมือนตอนที่ทำเพอร์เซปตรอนชั้นเดียวก็คือ เนื่องจากเราต้องการให้เซลล์ประสาทแต่ละตัวมีการทำหน้าที่ต่างกันไป ดังนั้นมันจะต้องมีความแตกต่างกัน ยิ่งมากยิ่งดี
แต่หากกำหนดน้ำหนักเริ่มต้นทุกตัวเป็น 0 หมดเท่ากับว่าทุกเซลล์จะมีการคำนวณที่เหมือนกันหมดตั้งแต่แรก พอเวลาปรับค่าน้ำหนักก็จะถูกปรับไปในทิศทางเดียวกันหมด เมื่อทุกตัวเหมือนกัน การมีเซลล์ประสาทหลายตัวก็ไม่ก่อให้เกิดประโยชน์อะไร
นี่คือเหตุผลที่จะให้ค่าน้ำหนักเริ่มต้นเป็น 0 ไม่ได้
ส่วนค่าไบแอส b ให้เป็น 0 ไปก็ไม่มีปัญหาอะไร โดยทั่วไปจึงถูกกำหนดเป็น 0 อยู่แล้ว
โดยทั่วไป w จะถูกกำหนดให้สุ่มโดยแจกแจงแบบเกาส์ แต่จะให้ความกว้าง σ เป็นเท่าไหร่นั้นไม่มีกฎเกณฑ์ตายตัว แต่ก็มีคนวิจัยคิดหาค่าที่เหมาะสมไว้อยู่
ค่าเริ่มต้นของซาวีเย โกลโร และ เหอ ไข่หมิง
ปี 2010 ได้มีการตีพิมพ์งานวิจัยเกี่ยวกับค่าตั้งต้นที่เหมาะสม โดย ซาวีเย โกลโร (Xavier Glorot) ระบุว่าเมื่อใช้ซอฟต์แม็กซ์เป็นฟังก์ชันกระตุ้นแล้ว ค่า σ ที่เหมาะสมที่สุดคือ
..(13.1)
โดย m คือจำนวนมิติขาเข้าของข้อมูล
การตั้งค่าเริ่มต้นแบบนี้จึงถูกเรียกว่าค่าตั้งต้นแบบซาวีเย (Xavier Initialization)
หลังจากนั้นในปี 2015 ได้มีการตีพิมพ์โดยเหอ ไข่หมิง (何恺明, Hé Kǎimíng) บอกว่าเมื่อใช้ ReLU เป็นฟังก์ชันกระตุ้น ค่า σ ที่เหมาะสมที่สุดคือ
..(13.2)
ค่าตั้งต้นแบบนี้จึงได้ถูกเรียกว่าค่าตั้งต้นแบบเหอ (Hé Initialization)
หลักเกณฑ์นี้จึงเป็นที่นิยมใช้โดยทั่วไป
ผลของค่าตั้งต้นที่ต่างกัน
ต่อไปจะทำการทดสอบเพื่อแสดงให้เห็นว่าค่าตั้งต้นที่ต่างกันนั้นทำให้ได้ผลต่างกันเป็นยังไง
ลองทำการสร้างข้อมูลจำนวนหนึ่งที่มีตัวแปรสักร้อยตัวขึ้นมาแบบสุ่ม แล้วให้ผ่านการด็อตกับน้ำหนักแล้วตามด้วยชั้นซิกมอยด์ รวมทั้งหมด ๕ ชั้น แล้วสร้างฮิสโทแกรมแสดงการกระจายของค่าเทียบดูว่าค่าตั้งต้น ๔ แบบต่างกัน คือ 1, 0.01, Xavier, Hé จะให้ผลต่างกันยังไง
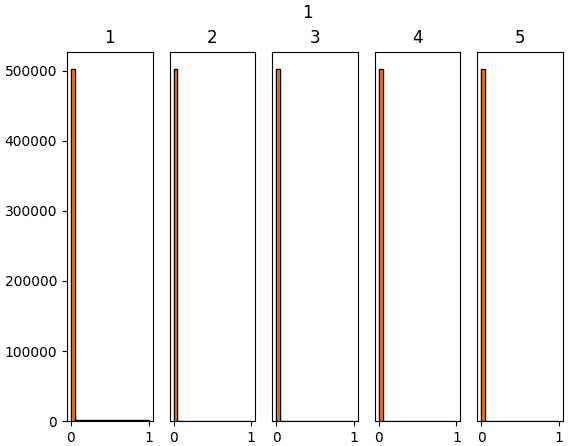
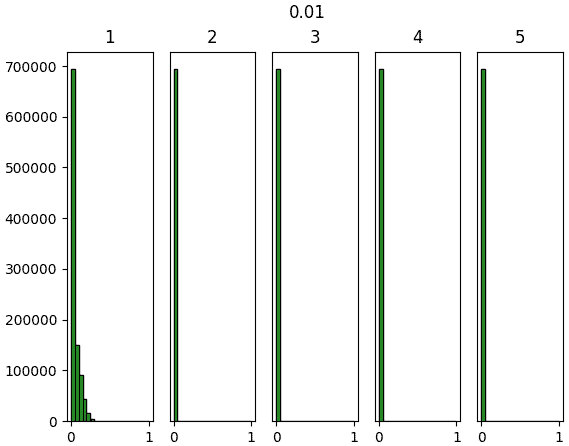
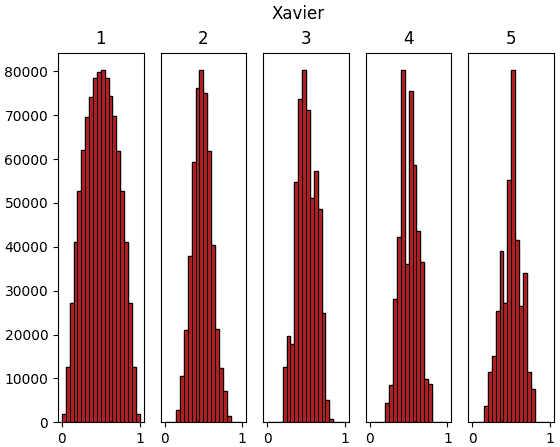
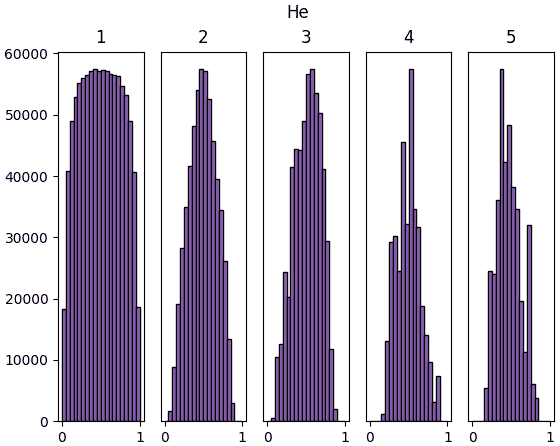
ผลที่ได้จะเห็นว่าค่าตั้งต้นแบบซาวีเยและแบบเหอ ไข่หมิงให้ผลออกมาดูค่อนข้างจะดี มีการกระจายสม่ำเสมอ ในขณะที่ถ้าใช้ sigma=1 ค่าจะไปกองอยู่ที่ 0 และ 1
ส่วนถ้าใช้ sigma=0.01 ค่าจะไปกองอยู่ตรงกลาง
การที่ค่าตัวแปรต่างๆกระจายสม่ำเสมอนั้นเป็นเรื่องดี เพราะแสดงว่าแต่ละตัวกำลังพิจารณาและอธิบายสิ่งที่ต่างกัน ถ้าไปกองอยู่ที่ค่าไหนมากๆแบบนั้นความหลากหลายก็จะลด ความหมายในการมีหลายๆเซลล์ก็จะหดหายไป
ต่อมาลองเปลี่ยนจากซิกมอยด์เป็น ReLU แล้วทำแบบเดิม ผลที่ได้จะเป็นแบบนี้
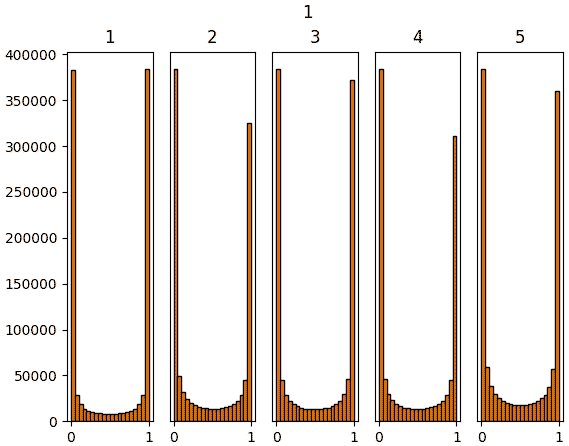
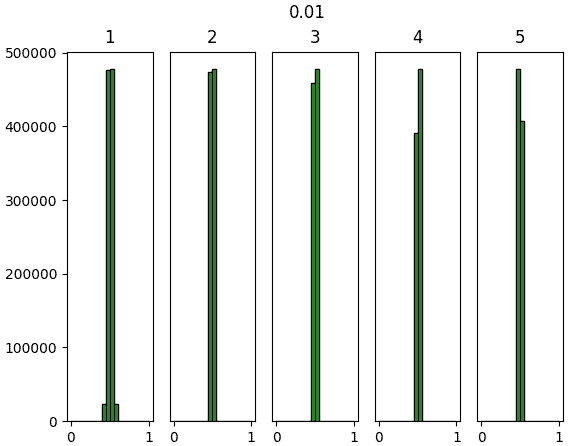
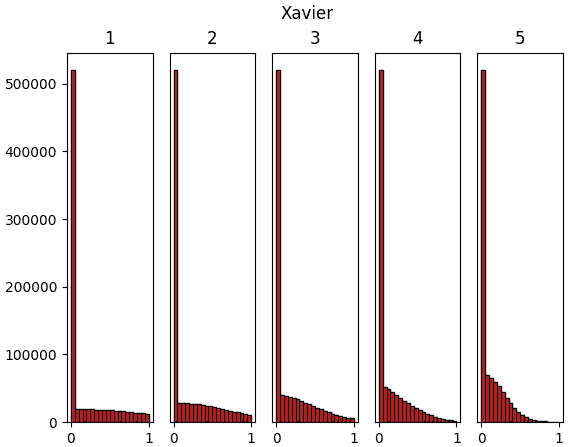
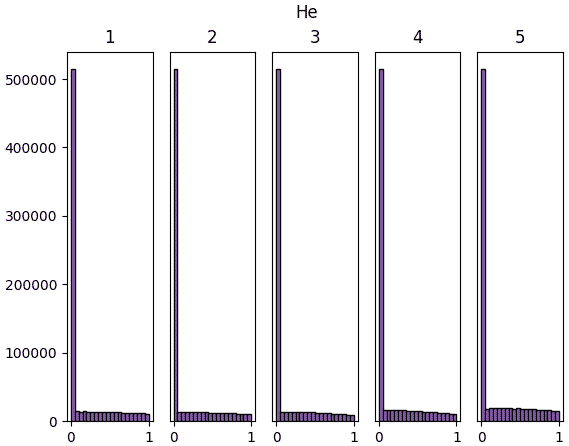
จะเห็นว่าสำหรับ ReLU นั้นค่าจะไปกองอยู่ที่ใกล้ 0 ซะมาก นั่นเป็นธรรมดาเพราะค่าที่ขาเข้าต่ำกว่า 0 จะกลายเป็น 0 หมด
แต่ถึงอย่างนั้นก็จะเห็นว่าหากใช้ค่าตั้งต้นแบบเหอ ไข่หมิงแล้ว สัดส่วนของค่าที่ห่างจาก 0 จะมีไม่น้อยเกินไป และกระจายค่อนข้างสม่ำเสมอ
โดยสรุปแล้วจะเห็นได้ว่าการเลือกค่าตั้งต้นให้เหมาะสมก็มีความสำคัญ บทต่อจากนี้ไปจะใช้หลักเกณฑ์นี้ในการเลือกค่าตั้งต้น
>> อ่านต่อ บทที่ ๑๔
ทำไมจึงไม่กำหนดค่าน้ำหนักเป็น 0
ตั้งแต่บทที่ ๘ นั้นเราได้เริ่มกำหนดค่าพารามิเตอร์น้ำหนัก w ตั้งต้นให้แจกแจงแบบเกาส์
สาเหตุที่ไม่กำหนดให้เป็น 0 ทั้งหมดเหมือนตอนที่ทำเพอร์เซปตรอนชั้นเดียวก็คือ เนื่องจากเราต้องการให้เซลล์ประสาทแต่ละตัวมีการทำหน้าที่ต่างกันไป ดังนั้นมันจะต้องมีความแตกต่างกัน ยิ่งมากยิ่งดี
แต่หากกำหนดน้ำหนักเริ่มต้นทุกตัวเป็น 0 หมดเท่ากับว่าทุกเซลล์จะมีการคำนวณที่เหมือนกันหมดตั้งแต่แรก พอเวลาปรับค่าน้ำหนักก็จะถูกปรับไปในทิศทางเดียวกันหมด เมื่อทุกตัวเหมือนกัน การมีเซลล์ประสาทหลายตัวก็ไม่ก่อให้เกิดประโยชน์อะไร
นี่คือเหตุผลที่จะให้ค่าน้ำหนักเริ่มต้นเป็น 0 ไม่ได้
ส่วนค่าไบแอส b ให้เป็น 0 ไปก็ไม่มีปัญหาอะไร โดยทั่วไปจึงถูกกำหนดเป็น 0 อยู่แล้ว
โดยทั่วไป w จะถูกกำหนดให้สุ่มโดยแจกแจงแบบเกาส์ แต่จะให้ความกว้าง σ เป็นเท่าไหร่นั้นไม่มีกฎเกณฑ์ตายตัว แต่ก็มีคนวิจัยคิดหาค่าที่เหมาะสมไว้อยู่
ค่าเริ่มต้นของซาวีเย โกลโร และ เหอ ไข่หมิง
ปี 2010 ได้มีการตีพิมพ์งานวิจัยเกี่ยวกับค่าตั้งต้นที่เหมาะสม โดย ซาวีเย โกลโร (Xavier Glorot) ระบุว่าเมื่อใช้ซอฟต์แม็กซ์เป็นฟังก์ชันกระตุ้นแล้ว ค่า σ ที่เหมาะสมที่สุดคือ
..(13.1)
โดย m คือจำนวนมิติขาเข้าของข้อมูล
การตั้งค่าเริ่มต้นแบบนี้จึงถูกเรียกว่าค่าตั้งต้นแบบซาวีเย (Xavier Initialization)
หลังจากนั้นในปี 2015 ได้มีการตีพิมพ์โดยเหอ ไข่หมิง (何恺明, Hé Kǎimíng) บอกว่าเมื่อใช้ ReLU เป็นฟังก์ชันกระตุ้น ค่า σ ที่เหมาะสมที่สุดคือ
..(13.2)
ค่าตั้งต้นแบบนี้จึงได้ถูกเรียกว่าค่าตั้งต้นแบบเหอ (Hé Initialization)
หลักเกณฑ์นี้จึงเป็นที่นิยมใช้โดยทั่วไป
ผลของค่าตั้งต้นที่ต่างกัน
ต่อไปจะทำการทดสอบเพื่อแสดงให้เห็นว่าค่าตั้งต้นที่ต่างกันนั้นทำให้ได้ผลต่างกันเป็นยังไง
ลองทำการสร้างข้อมูลจำนวนหนึ่งที่มีตัวแปรสักร้อยตัวขึ้นมาแบบสุ่ม แล้วให้ผ่านการด็อตกับน้ำหนักแล้วตามด้วยชั้นซิกมอยด์ รวมทั้งหมด ๕ ชั้น แล้วสร้างฮิสโทแกรมแสดงการกระจายของค่าเทียบดูว่าค่าตั้งต้น ๔ แบบต่างกัน คือ 1, 0.01, Xavier, Hé จะให้ผลต่างกันยังไง
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1/(1+np.exp(-x))
def relu(x):
return np.maximum(0,x)
m = 100 # จำนวนตัวแปรในแต่ละชั้น
n = 10000 # จำนวนข้อมูล
n_chan = 5 # จำนวนชั้น
x = np.random.normal(0,1,[n,m]) # สุ่มตัวแปรต้น
sigma = [1,0.01,1./np.sqrt(m),np.sqrt(2./m)]
for j in range(4):
h = x
plt.figure().suptitle(['1','0.01','Xavier','Hé'][j])
for i in range(n_chan):
w = np.random.normal(0,sigma[j],[m,m])
a = np.dot(h,w) # +0
h = sigmoid(a)
#h = relu(a) # รอบหน้าลองเปลี่ยนมาใช้ ReLU
plt.subplot(1,n_chan,i+1)
plt.title('%d'%(i+1))
if(i>0):
plt.yticks([],[])
plt.hist(h.flatten(),20,(0,1),ec='k',color='C%d'%(j+1))
plt.show()



ผลที่ได้จะเห็นว่าค่าตั้งต้นแบบซาวีเยและแบบเหอ ไข่หมิงให้ผลออกมาดูค่อนข้างจะดี มีการกระจายสม่ำเสมอ ในขณะที่ถ้าใช้ sigma=1 ค่าจะไปกองอยู่ที่ 0 และ 1
ส่วนถ้าใช้ sigma=0.01 ค่าจะไปกองอยู่ตรงกลาง
การที่ค่าตัวแปรต่างๆกระจายสม่ำเสมอนั้นเป็นเรื่องดี เพราะแสดงว่าแต่ละตัวกำลังพิจารณาและอธิบายสิ่งที่ต่างกัน ถ้าไปกองอยู่ที่ค่าไหนมากๆแบบนั้นความหลากหลายก็จะลด ความหมายในการมีหลายๆเซลล์ก็จะหดหายไป
ต่อมาลองเปลี่ยนจากซิกมอยด์เป็น ReLU แล้วทำแบบเดิม ผลที่ได้จะเป็นแบบนี้




จะเห็นว่าสำหรับ ReLU นั้นค่าจะไปกองอยู่ที่ใกล้ 0 ซะมาก นั่นเป็นธรรมดาเพราะค่าที่ขาเข้าต่ำกว่า 0 จะกลายเป็น 0 หมด
แต่ถึงอย่างนั้นก็จะเห็นว่าหากใช้ค่าตั้งต้นแบบเหอ ไข่หมิงแล้ว สัดส่วนของค่าที่ห่างจาก 0 จะมีไม่น้อยเกินไป และกระจายค่อนข้างสม่ำเสมอ
โดยสรุปแล้วจะเห็นได้ว่าการเลือกค่าตั้งต้นให้เหมาะสมก็มีความสำคัญ บทต่อจากนี้ไปจะใช้หลักเกณฑ์นี้ในการเลือกค่าตั้งต้น
>> อ่านต่อ บทที่ ๑๔
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy