ทำความเข้าใจเอนโทรปีไขว้และความควรจะเป็น
เขียนเมื่อ 2018/08/14 18:16
แก้ไขล่าสุด 2021/09/28 16:42
เวลาที่เขียนโปรแกรมแก้ปัญหาการแบ่งกลุ่มด้วยวิธีการวิเคราะห์การถดถอยโลจิสติก (逻辑回归, logistic regression) หรือโครงข่ายประสาทเทียม ปกติเราจะใช้ค่าเอนโทรปีไขว้ (交叉熵, cross entropy) เป็นฟังก์ชันค่าเสียหาย คือฟังก์ชันเป้าหมายที่ต้องการลดให้ต่ำที่สุด
ที่มาของค่าเอนโทรปีไขว้นี้มาจากการพิจารณาค่าควรจะเป็น (似然函数, likelihood)
ภาษาไทยใช้คำคล้ายๆกันแต่ "ค่าควรจะเป็น" กับ "ความน่าจะเป็น" เป็นคนละคำกัน
ความน่าจะเป็น (概率, probabilità) คือค่าที่บอกว่าเหตุการณ์ที่กำลังพิจารณาอยู่นั้นมีโอกาสเกิดแค่ไหน
เช่น เวลาโยนเหรียญ ถ้าความน่าจะเป็นที่จะออกหัวคือ 0.6 แสดงว่าหากโยนสัก 100 ครั้ง ก็ควรจะได้หัว 60 ครั้ง
ส่วนค่าควรจะเป็น คือค่าที่บอกว่าความน่าจะเป็นที่เราคาดเดานั้นสมเหตุสมผลแค่ไหนถ้าพิจารณาจากผลลัพธ์ที่เกิดขึ้น
ซึ่งก็คือคำนวณว่าผลลัพธ์ที่เกิดขึ้นนั้นมีโอกาสเกิดขึ้นแค่ไหนจากความน่าจะเป็นที่เราคาดการณ์ไว้ ถ้าความน่าจะเป็นมากยิ่งแสดงว่าสมเหตุสมผล
เช่น โยนเหรียญครั้งนึง ออกก้อย แบบนั้นค่าควรจะเป็นก็จะเท่ากับความน่าจะเป็นที่จะออกก้อย ซึ่งเท่ากับ 1 ลบด้วยความน่าจะเป็นที่จะออกหัว
สมมุติว่าเราทายว่าเหรียญอันนึงมีความน่าจะเป็นที่จะออกหัว 0.6 ก็จะได้ค่าควรจะเป็นเป็น 1-0.6=0.4
แต่ถ้าทายว่าเป็น 0 ก็จะได้ 1-0=1 ซึ่งตรงนี้บ่งบอกว่าหากทายว่าความน่าจะเป็นเป็น 0 จะมีค่าควรจะเป็นสูงกว่า
หากเขียนกราฟแสดงความสัมพันธ์ระหว่างค่าความน่าจะเป็นที่คาดเดาไว้และค่าควรจะเป็นที่ได้จะได้แบบนี้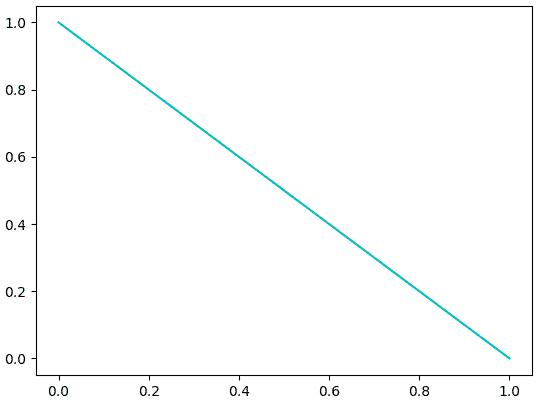
แบบนี้จะเห็นว่าหากทายว่าความน่าจะเป็นเป็น 0 ดูจะสมเหตุสมผลที่สุด
แต่ว่าหากโยนเหรียญอีกครั้งนึงแล้วปรากฎว่าได้หัว เท่ากับเป็นก้อยครังนึงหัวครั้งนึงแล้ว แบบนั้นค่าควรจะเป็นจะกลายเป็นเท่าไหร่?
ปกติแล้วความน่าจะเป็นของเหตุการณ์สองเหตุการณ์ที่ไม่ได้เกี่ยวข้องกันเลยจะคำนวณได้โดยเอาความน่าจะเป็นของทั้งสองนั้นมาคูณกัน
ดังนั้นกรณีนี้ต้องเอาความน่าจะเป็นที่จะโยนเหรียญได้หัวมาคูณกับความน่าจะเป็นที่จะโดยได้ก้อย
หากทายว่าความน่าจะเป็นเป็น 0.6 แบบนั้นค่าควรจะเป็นก็จะเป็น (1-0.6)×0.6 = 0.24
แต่ถ้าทายว่าเป็น 0 จะได้ (1-0)×0 = 0
กลายเป็นว่าการทายว่าความน่าจะเป็นเป็น 0 เป็นเรื่องไม่สมเหตุสมผลไปทันที ซึ่งก็เป็นธรรมดา เพราะหากความน่าจะเป็นเป็น 0 แสดงว่าต้องไม่มีโอกาสเกิดขึ้นเลย การที่มันเกิดขึ้นแล้วครั้งนึงแสดงว่าความน่าจะเป็นต้องไม่ใช่ 0
ในเมื่อการที่ความน่าจะเป็นเป็น 0 เป็นสิ่งที่ไม่ควรจะเป็น ดังนั้นค่าควรจะเป็นจึงมีค่าเป็น 0
หากวาดกราฟใหม่ก็จะได้แบบนี้
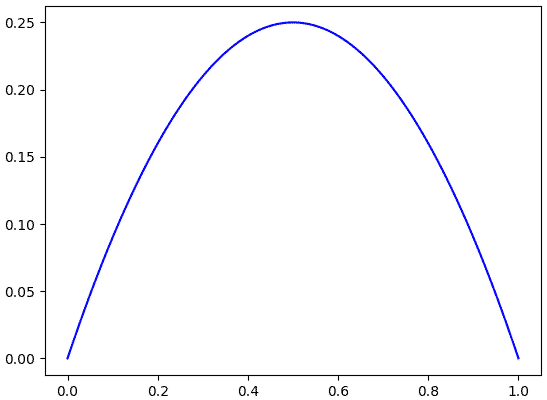
กลายเป็นว่าค่าสูงสุดอยู่ที่ 0.5 ซึ่งก็สมเหตุสมผลดี เพราะออกหัวออกก้อยเท่ากันการทายว่าความน่าจะเป็น 0.5 ย่อมดีที่สุด
ถ้าโยนอีกครั้งได้หัว ค่าควรจะเป็นก็จะกลายเป็น (1-p)×p×p
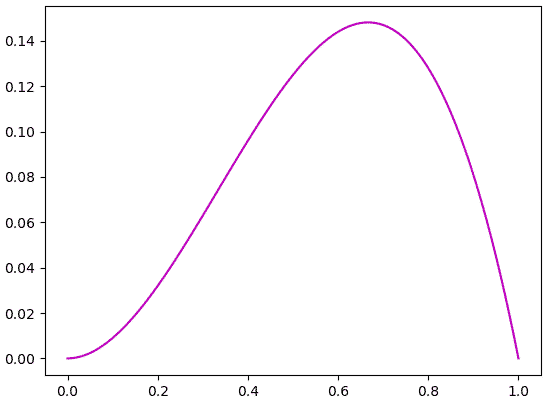
คราวนี้ค่าสูงสุดอยู่ที่ 2/3=0.6666... แทน ซึ่งก็สมเหตุสมผลดีที่ค่าความจะเป็นสูงสุดจะมีค่าเท่ากับสัดส่วนที่ออกหัว เป็นไปตามสามัญสำนึกที่ว่าถ้าความน่าจะเป็นเป็นเท่าไหร่ โอกาสที่จะได้ตามสัดส่วนนั้นย่อมสูงสุด
หากลองโยนเหรียญหลายๆครั้งก็จะพบว่าค่าควรจะเป็นคือ
..(1)
โดย n0 คือจำนวนครั้งที่ออกก้อย n1 คือจำนวนครั้งที่ออกหัว
ตัวอย่างเช่นออกก้อย 9 ครั้ง ออกหัว 18 ครั้ง จะได้ว่า
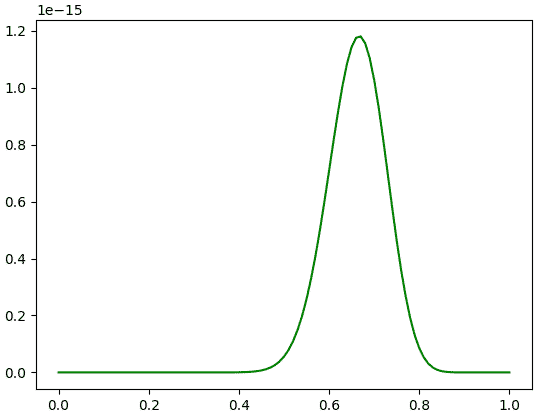
ที่น่าสังเกตอย่างนึงก็คือ จุดสูงสุดของกรณีนี้อยู่ที่ 0.6666... เหมือนกัน แต่กราฟดูผอมแคบลงเยอะ
นั่นหมายความว่ายิ่งทดลองจำนวนมาก ค่าควรจะเป็นในการเดาความน่าจะเป็นแต่ละค่ายิ่งต่างกันชัด ดังนั้นยิ่งมั่นใจในการเดาได้มากขึ้น นี่คือเหตุผลที่เวลาทดลองทำอะไรเพื่อหาความน่าจะเป็นจะต้องทำหลายครั้งมากที่สุดเท่าที่จะเป็นไปได้
ทีนี้จะเห็นว่าการคำนวณค่าควรจะเป็นนี้จะต้องคูณกันไปเรื่อยๆ แบบนี้ดูแล้วไม่ค่อยสะดวก อีกทั้งค่ายิ่งเล็กลงเรื่อยๆเมื่อคูณกันมากเข้า
ดังนั้นโดยทั่วไปเวลาคำนวณคนจึงมักคำนวณค่า ln ของค่าควรจะเป็นแทน และโดยสมบัติของ ln แล้วจะได้ว่า
..(2)
ต่อให้ใส่ ln ไป ค่าที่สูงสุดก็ยังเป็นค่าสูงสุดไม่เปลี่ยนแปลง แต่จะได้ค่าที่ดูอ่านง่ายขึ้นเยอะ
ทีนี้กลับมาที่เรื่องของเอนโทรปีไขว้ในการวิเคราะห์การถดถอยโลจิสติก
เอนโทรปีไขว้คือค่าลบของ ln ของค่าควรจะเป็น
..(3)
สาเหตุที่ต้องเป็นค่าลบก็คือปกติแล้วค่าควรจะเป็นมีค่าต่ำกว่า 0 ดังนั้น ln ก็จะติดลบ ถ้าใส่ลบให้เป็นค่าบวกจะดูดีกว่า อีกทั้งปกติปัญหาการหาค่าต่ำสุดนั้นเป็นที่นิยมมากกว่าการหาค่าสูงสุด
ในปัญหาการแบ่งกลุ่ม ๒ กลุ่มปกติจะให้ค่าคำตอบทั้งสองแทนด้วยเลข 0 และ 1 ให้กลุ่มนึงแทนด้วยเลข 0 อีกกลุ่มแทนด้วยเลข 1
ด้วยการวิเคราะห์การถดถอยโลจิสติกเราจะใช้ฟังก์ชันซิกมอยด์คำนวณ ซึ่งผลที่ได้ค่าที่ได้ออกมาจะเป็นค่าที่อยู่ระหว่าง 0 ถึง 1 ซึ่งค่านี้จะบอกความน่าจะเป็นที่คำตอบจะเป็นกลุ่ม 1
แบบนี้ถ้าคำตอบจริงๆเป็น 1 เราก็จะได้ค่าเอนโทรปีไขว้เป็น
..(4)
แต่ถ้าคำตอบเป็น 0 เราจะได้ค่าเป็น
..(5)
สุดท้ายสามารถมาเขียนเป็นรูปทั่วไปได้ว่า
..(6)
โดย z คือค่าคำตอบ จะเห็นว่าถ้าคำตอบเป็น 0 ตัวหลังก็จะหายไป กลับไปสู่สมการ (4) แต่ถ้าเป็น 1 ตัวหน้าจะหาย กลับไปสู่สมการ (5)
ต่อมา พิจารณาปัญหาการแบ่งกลุ่มมากกว่าสองกลุ่ม กรณีนี้จะใช้ฟังก์ชันซอฟต์แม็กซ์เพื่อหาความน่าจะเป็นที่คำตอบจะเป็นค่าในแต่ละกลุ่ม ส่วนคำตอบจริงจะอยู่ในรูปวันฮ็อต (one-hot) คือเป็น 1 แต่คำตอบที่ใช่ ส่วนที่เหลือเป็น 0
แบบนี้ค่าควรจะเป็นก็คือค่าความน่าจะเป็นที่เราทายไว้สำหรับกลุ่มที่ 2 ก็คือ 0.6
เช่นถ้าเป็นปัญหาแบ่งกลุ่ม ๕ กลุ่ม ถ้าคำตอบจริงเป็นกลุ่มที่ 2 จะได้ว่าคำตอบคือ z=[0,1,0,0,0]
แล้วสมมุติเราทำนายค่าความน่าจะเป็นที่จะเป็นแต่ละกลุ่มไว้ว่า p=[0.15,0.6,0.1,0.05,0.1]
เนื่องจากคำตอบจริงมีเพียงตัวเดียวที่เป็น 1 ที่เหลือเป็น 0 ดังนั้นค่าควรจะเป็นก็จะขึ้นอยู่กับความน่าจะเป็นที่เราทำนายให้กลุ่มนั้น ค่าที่ทายให้กลุ่มอื่นจะไม่มีผล
ส่วนค่าเอนโทรปีไขว้ก็คือ -ln(0.6)
ซึ่งตรงนี้ที่จริงถ้าเขียนให้อยู่ในรูปทั่วไปแล้วก็คือค่าควรจะเป็นคือเอาความน่าจะเป็นมายกกำลัง z แล้วนำทั้งหมดมาคูณกัน
นั่นคือ 0.150×0.61×0.10×0.050×0.11 = 0.6
ส่วนเอนโทรปีไขว้เป็น -0×ln(0.15)-1×ln(0.6)-0×ln(0.1)^(0)-0×ln(0.05)-0×ln(0.1)
หากเขียนเป็นสูตรคำนวณโดยทั่วไปได้ว่า
..(7)
(ซึ่งถ้ามีแค่สองกลุ่มจะได้ว่า p0=1-p1 และ z0=1-z1 แล้วก็จะกลับไปสู่สมการ (6))
อย่างไรก็ตามโดยทั่วไปแล้วในเมื่อที่เป็น 1 จะมีแค่ค่าเดียวที่เหลือเป็น 0 ส่วนที่เป็น 0 นั้นไม่จำเป็นต้องคำนวณจริงๆ
ดังนั้นเวลาที่คำนวณค่าเอนโทรปีของจำนวนมากๆหลายตัวพร้อมกันแล้ว ในการคำนวณจริงๆแล้วแทนที่จะคำนวณตรงๆตามสมการ (ซึ่งต้องคำนวณค่า ln ของทุกตัวทั้งที่สุดท้ายแล้วค่าที่ได้จริงๆเป็นแค่ไม่กี่ตัวในนั้น) ถ้าเราใช้วิธีการกรองเอาเฉพาะที่เป็น 1 มาคำนวณจะเร็วกว่า
เพื่อให้เห็นความแตกต่าง ลองเปรียบเทียบเวลาดู สมมุติว่าเป็นปัญหาแบ่งกลุ่ม 100 กลุ่ม ข้อมูลมี 100000 ตัว อาจสร้างข้อมูลแบบสุ่มได้แบบนี้
ทั้งหมดนี้เป็นที่มาของค่าเอนโทรปีไขว้ที่นิยมใช้กัน
สรุปง่ายๆก็คือ เวลาเราคำนวณฟังก์ชันซิกมอยด์หรือซอฟต์แม็กซ์ ผลที่ได้มาคือค่าความน่าจะเป็น แล้วค่าควรจะเป็นคือสิ่งที่จะบอกว่าความน่าจะเป็นที่เราได้มานั้นสมเหตุสมผลแค่ไหน ส่วนเอนโทรปีไขว้คือ -ln(ค่าควรจะเป็น) ดังนั้นจึงเป็นค่าที่ยิ่งน้อยยิ่งดี และมันจึงกลายมาเป็นฟังก์ชันค่าเสียหายที่เป็นเป้าหมายที่เราต้องการลดให้น้อยที่สุด
ที่มาของค่าเอนโทรปีไขว้นี้มาจากการพิจารณาค่าควรจะเป็น (似然函数, likelihood)
ภาษาไทยใช้คำคล้ายๆกันแต่ "ค่าควรจะเป็น" กับ "ความน่าจะเป็น" เป็นคนละคำกัน
ความน่าจะเป็น (概率, probabilità) คือค่าที่บอกว่าเหตุการณ์ที่กำลังพิจารณาอยู่นั้นมีโอกาสเกิดแค่ไหน
เช่น เวลาโยนเหรียญ ถ้าความน่าจะเป็นที่จะออกหัวคือ 0.6 แสดงว่าหากโยนสัก 100 ครั้ง ก็ควรจะได้หัว 60 ครั้ง
ส่วนค่าควรจะเป็น คือค่าที่บอกว่าความน่าจะเป็นที่เราคาดเดานั้นสมเหตุสมผลแค่ไหนถ้าพิจารณาจากผลลัพธ์ที่เกิดขึ้น
ซึ่งก็คือคำนวณว่าผลลัพธ์ที่เกิดขึ้นนั้นมีโอกาสเกิดขึ้นแค่ไหนจากความน่าจะเป็นที่เราคาดการณ์ไว้ ถ้าความน่าจะเป็นมากยิ่งแสดงว่าสมเหตุสมผล
เช่น โยนเหรียญครั้งนึง ออกก้อย แบบนั้นค่าควรจะเป็นก็จะเท่ากับความน่าจะเป็นที่จะออกก้อย ซึ่งเท่ากับ 1 ลบด้วยความน่าจะเป็นที่จะออกหัว
สมมุติว่าเราทายว่าเหรียญอันนึงมีความน่าจะเป็นที่จะออกหัว 0.6 ก็จะได้ค่าควรจะเป็นเป็น 1-0.6=0.4
แต่ถ้าทายว่าเป็น 0 ก็จะได้ 1-0=1 ซึ่งตรงนี้บ่งบอกว่าหากทายว่าความน่าจะเป็นเป็น 0 จะมีค่าควรจะเป็นสูงกว่า
หากเขียนกราฟแสดงความสัมพันธ์ระหว่างค่าความน่าจะเป็นที่คาดเดาไว้และค่าควรจะเป็นที่ได้จะได้แบบนี้
import numpy as np
import matplotlib.pyplot as plt
p = np.linspace(0,1,101)
y = 1-p
plt.plot(p,y,'c')
plt.show()
แบบนี้จะเห็นว่าหากทายว่าความน่าจะเป็นเป็น 0 ดูจะสมเหตุสมผลที่สุด
แต่ว่าหากโยนเหรียญอีกครั้งนึงแล้วปรากฎว่าได้หัว เท่ากับเป็นก้อยครังนึงหัวครั้งนึงแล้ว แบบนั้นค่าควรจะเป็นจะกลายเป็นเท่าไหร่?
ปกติแล้วความน่าจะเป็นของเหตุการณ์สองเหตุการณ์ที่ไม่ได้เกี่ยวข้องกันเลยจะคำนวณได้โดยเอาความน่าจะเป็นของทั้งสองนั้นมาคูณกัน
ดังนั้นกรณีนี้ต้องเอาความน่าจะเป็นที่จะโยนเหรียญได้หัวมาคูณกับความน่าจะเป็นที่จะโดยได้ก้อย
หากทายว่าความน่าจะเป็นเป็น 0.6 แบบนั้นค่าควรจะเป็นก็จะเป็น (1-0.6)×0.6 = 0.24
แต่ถ้าทายว่าเป็น 0 จะได้ (1-0)×0 = 0
กลายเป็นว่าการทายว่าความน่าจะเป็นเป็น 0 เป็นเรื่องไม่สมเหตุสมผลไปทันที ซึ่งก็เป็นธรรมดา เพราะหากความน่าจะเป็นเป็น 0 แสดงว่าต้องไม่มีโอกาสเกิดขึ้นเลย การที่มันเกิดขึ้นแล้วครั้งนึงแสดงว่าความน่าจะเป็นต้องไม่ใช่ 0
ในเมื่อการที่ความน่าจะเป็นเป็น 0 เป็นสิ่งที่ไม่ควรจะเป็น ดังนั้นค่าควรจะเป็นจึงมีค่าเป็น 0
หากวาดกราฟใหม่ก็จะได้แบบนี้
y = (1-p)*p
plt.plot(p,y,'b')
plt.show()
กลายเป็นว่าค่าสูงสุดอยู่ที่ 0.5 ซึ่งก็สมเหตุสมผลดี เพราะออกหัวออกก้อยเท่ากันการทายว่าความน่าจะเป็น 0.5 ย่อมดีที่สุด
ถ้าโยนอีกครั้งได้หัว ค่าควรจะเป็นก็จะกลายเป็น (1-p)×p×p
p = np.linspace(0,1,101)
y = (1-p)*p*p
plt.plot(p,y,'m')
plt.show()
คราวนี้ค่าสูงสุดอยู่ที่ 2/3=0.6666... แทน ซึ่งก็สมเหตุสมผลดีที่ค่าความจะเป็นสูงสุดจะมีค่าเท่ากับสัดส่วนที่ออกหัว เป็นไปตามสามัญสำนึกที่ว่าถ้าความน่าจะเป็นเป็นเท่าไหร่ โอกาสที่จะได้ตามสัดส่วนนั้นย่อมสูงสุด
หากลองโยนเหรียญหลายๆครั้งก็จะพบว่าค่าควรจะเป็นคือ
..(1)
โดย n0 คือจำนวนครั้งที่ออกก้อย n1 คือจำนวนครั้งที่ออกหัว
ตัวอย่างเช่นออกก้อย 9 ครั้ง ออกหัว 18 ครั้ง จะได้ว่า
n0 = 18
n1 = 36
y = (1-p)**n0*p**n1
plt.plot(p,y,'g')
plt.show()
ที่น่าสังเกตอย่างนึงก็คือ จุดสูงสุดของกรณีนี้อยู่ที่ 0.6666... เหมือนกัน แต่กราฟดูผอมแคบลงเยอะ
นั่นหมายความว่ายิ่งทดลองจำนวนมาก ค่าควรจะเป็นในการเดาความน่าจะเป็นแต่ละค่ายิ่งต่างกันชัด ดังนั้นยิ่งมั่นใจในการเดาได้มากขึ้น นี่คือเหตุผลที่เวลาทดลองทำอะไรเพื่อหาความน่าจะเป็นจะต้องทำหลายครั้งมากที่สุดเท่าที่จะเป็นไปได้
ทีนี้จะเห็นว่าการคำนวณค่าควรจะเป็นนี้จะต้องคูณกันไปเรื่อยๆ แบบนี้ดูแล้วไม่ค่อยสะดวก อีกทั้งค่ายิ่งเล็กลงเรื่อยๆเมื่อคูณกันมากเข้า
ดังนั้นโดยทั่วไปเวลาคำนวณคนจึงมักคำนวณค่า ln ของค่าควรจะเป็นแทน และโดยสมบัติของ ln แล้วจะได้ว่า
..(2)
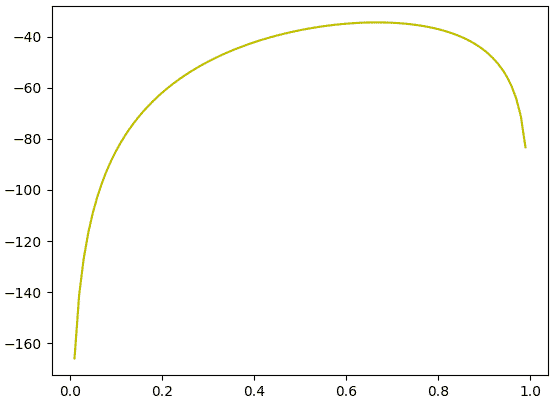
ต่อให้ใส่ ln ไป ค่าที่สูงสุดก็ยังเป็นค่าสูงสุดไม่เปลี่ยนแปลง แต่จะได้ค่าที่ดูอ่านง่ายขึ้นเยอะ
ln_y = n0*np.log(1-p)+n1*np.log(p)
plt.plot(p,ln_y,'y')
plt.show()
ทีนี้กลับมาที่เรื่องของเอนโทรปีไขว้ในการวิเคราะห์การถดถอยโลจิสติก
เอนโทรปีไขว้คือค่าลบของ ln ของค่าควรจะเป็น
..(3)
สาเหตุที่ต้องเป็นค่าลบก็คือปกติแล้วค่าควรจะเป็นมีค่าต่ำกว่า 0 ดังนั้น ln ก็จะติดลบ ถ้าใส่ลบให้เป็นค่าบวกจะดูดีกว่า อีกทั้งปกติปัญหาการหาค่าต่ำสุดนั้นเป็นที่นิยมมากกว่าการหาค่าสูงสุด
ในปัญหาการแบ่งกลุ่ม ๒ กลุ่มปกติจะให้ค่าคำตอบทั้งสองแทนด้วยเลข 0 และ 1 ให้กลุ่มนึงแทนด้วยเลข 0 อีกกลุ่มแทนด้วยเลข 1
ด้วยการวิเคราะห์การถดถอยโลจิสติกเราจะใช้ฟังก์ชันซิกมอยด์คำนวณ ซึ่งผลที่ได้ค่าที่ได้ออกมาจะเป็นค่าที่อยู่ระหว่าง 0 ถึง 1 ซึ่งค่านี้จะบอกความน่าจะเป็นที่คำตอบจะเป็นกลุ่ม 1
แบบนี้ถ้าคำตอบจริงๆเป็น 1 เราก็จะได้ค่าเอนโทรปีไขว้เป็น
..(4)
แต่ถ้าคำตอบเป็น 0 เราจะได้ค่าเป็น
..(5)
สุดท้ายสามารถมาเขียนเป็นรูปทั่วไปได้ว่า
..(6)
โดย z คือค่าคำตอบ จะเห็นว่าถ้าคำตอบเป็น 0 ตัวหลังก็จะหายไป กลับไปสู่สมการ (4) แต่ถ้าเป็น 1 ตัวหน้าจะหาย กลับไปสู่สมการ (5)
ต่อมา พิจารณาปัญหาการแบ่งกลุ่มมากกว่าสองกลุ่ม กรณีนี้จะใช้ฟังก์ชันซอฟต์แม็กซ์เพื่อหาความน่าจะเป็นที่คำตอบจะเป็นค่าในแต่ละกลุ่ม ส่วนคำตอบจริงจะอยู่ในรูปวันฮ็อต (one-hot) คือเป็น 1 แต่คำตอบที่ใช่ ส่วนที่เหลือเป็น 0
แบบนี้ค่าควรจะเป็นก็คือค่าความน่าจะเป็นที่เราทายไว้สำหรับกลุ่มที่ 2 ก็คือ 0.6
เช่นถ้าเป็นปัญหาแบ่งกลุ่ม ๕ กลุ่ม ถ้าคำตอบจริงเป็นกลุ่มที่ 2 จะได้ว่าคำตอบคือ z=[0,1,0,0,0]
แล้วสมมุติเราทำนายค่าความน่าจะเป็นที่จะเป็นแต่ละกลุ่มไว้ว่า p=[0.15,0.6,0.1,0.05,0.1]
เนื่องจากคำตอบจริงมีเพียงตัวเดียวที่เป็น 1 ที่เหลือเป็น 0 ดังนั้นค่าควรจะเป็นก็จะขึ้นอยู่กับความน่าจะเป็นที่เราทำนายให้กลุ่มนั้น ค่าที่ทายให้กลุ่มอื่นจะไม่มีผล
ส่วนค่าเอนโทรปีไขว้ก็คือ -ln(0.6)
ซึ่งตรงนี้ที่จริงถ้าเขียนให้อยู่ในรูปทั่วไปแล้วก็คือค่าควรจะเป็นคือเอาความน่าจะเป็นมายกกำลัง z แล้วนำทั้งหมดมาคูณกัน
นั่นคือ 0.150×0.61×0.10×0.050×0.11 = 0.6
ส่วนเอนโทรปีไขว้เป็น -0×ln(0.15)-1×ln(0.6)-0×ln(0.1)^(0)-0×ln(0.05)-0×ln(0.1)
หากเขียนเป็นสูตรคำนวณโดยทั่วไปได้ว่า
..(7)
(ซึ่งถ้ามีแค่สองกลุ่มจะได้ว่า p0=1-p1 และ z0=1-z1 แล้วก็จะกลับไปสู่สมการ (6))
อย่างไรก็ตามโดยทั่วไปแล้วในเมื่อที่เป็น 1 จะมีแค่ค่าเดียวที่เหลือเป็น 0 ส่วนที่เป็น 0 นั้นไม่จำเป็นต้องคำนวณจริงๆ
ดังนั้นเวลาที่คำนวณค่าเอนโทรปีของจำนวนมากๆหลายตัวพร้อมกันแล้ว ในการคำนวณจริงๆแล้วแทนที่จะคำนวณตรงๆตามสมการ (ซึ่งต้องคำนวณค่า ln ของทุกตัวทั้งที่สุดท้ายแล้วค่าที่ได้จริงๆเป็นแค่ไม่กี่ตัวในนั้น) ถ้าเราใช้วิธีการกรองเอาเฉพาะที่เป็น 1 มาคำนวณจะเร็วกว่า
เพื่อให้เห็นความแตกต่าง ลองเปรียบเทียบเวลาดู สมมุติว่าเป็นปัญหาแบ่งกลุ่ม 100 กลุ่ม ข้อมูลมี 100000 ตัว อาจสร้างข้อมูลแบบสุ่มได้แบบนี้
n = 100000 # จำนวนข้อมูล
m = 100 # จำนวนกลุ่ม
z = np.random.randint(0,m,n) # สุ่มคำตอบ n ตัว
z = z[:,None]==np.arange(m) # ทำให้เป็น one-hot
p = np.random.random([n,m]) # สุ่มความน่าจะเป็นทั้ง m กลุ่มของข้อมูล n ตัว
p /= p.sum(1)[:,None] # ทำให้รวมกันแล้วเป็น 1 ในทุกแถวimport time
# แบบคำนวณตามสมการ
t1 = time.time()
-(z*np.log(p)).sum()
print(time.time()-t1) # 0.37312865257263184
# แบบกรองแล้วคำนวณ
t1 = time.time()
-(np.log(p[z])).sum()
print(time.time()-t1) # 0.011081457138061523ทั้งหมดนี้เป็นที่มาของค่าเอนโทรปีไขว้ที่นิยมใช้กัน
สรุปง่ายๆก็คือ เวลาเราคำนวณฟังก์ชันซิกมอยด์หรือซอฟต์แม็กซ์ ผลที่ได้มาคือค่าความน่าจะเป็น แล้วค่าควรจะเป็นคือสิ่งที่จะบอกว่าความน่าจะเป็นที่เราได้มานั้นสมเหตุสมผลแค่ไหน ส่วนเอนโทรปีไขว้คือ -ln(ค่าควรจะเป็น) ดังนั้นจึงเป็นค่าที่ยิ่งน้อยยิ่งดี และมันจึงกลายมาเป็นฟังก์ชันค่าเสียหายที่เป็นเป้าหมายที่เราต้องการลดให้น้อยที่สุด