[python] แยกแยะภาพตัวเลขที่เขียนด้วยลายมือด้วยวิธีการเพื่อนบ้านใกล้สุด k ตัว
เขียนเมื่อ 2017/11/02 18:13
แก้ไขล่าสุด 2021/09/28 16:42
หลังจากที่คราวก่อนแนะนำการแยกภาพตัวเลขในข้อมูล MNIST แล้ว https://phyblas.hinaboshi.com/20170922

ครั้งก่อนนั้นใช้วิธีการวิเคราะห์การถดถอยโลจิสติก แต่คราวนี้จะลองเปลี่ยนมาใช้วิธีการเพื่อนบ้านใกล้สุด k ตัว (KNN) ดูบ้าง
รายละเอียดเกี่ยวกับข้อมูลตัวเลข MNIST รวมถึงวิธีการดึงข้อมูลมาได้เขียนถึงไปในบทความนั้นแล้ว ในที่นี้จะไม่กล่าวถึงซ้ำอีก
สำหรับวิธีการเพื่อนบ้านใกล้สุด k ตัวนั้น ก่อนหน้านี้ได้เขียนวิธีการสร้างคลาสไปใน https://phyblas.hinaboshi.com/20171028
เพียงแต่ว่าหากนำมาใช้กับข้อมูล MNIST ทั้งๆอย่างนั้นเลยจะมีปัญหาได้ เพราะเนื่องจากขนาดของข้อมูลซึ่งมีขนาดใหญ่มาก จึงยังต้องมีการดัดแปลงอีกสักหน่อยเพื่อใช้
ข้อมูล MNIST มีจำนวนมิติมากถึง 784 และจำนวนภาพก็มากถึง 70000 ภาพ หมายความว่าอาเรย์มีขนาด 54880000
ในคลาสที่สร้างไว้นั้นมีขั้นตอนที่มีการสร้างอาเรย์ขนาดมหึมาขึ้น คือ X[None]-self.X[:,None]
ซึ่งหากใช้ข้อมูลทั้งหมด 70000 ภาพในการเรียนรู้ หมายความว่าอาเรย์นี้จะมีขนาด 70000×784×จำนวนภาพที่จะหาคำตอบ
ปกติการสร้างอาเรย์ขึ้นมาเพื่อคำนวณอะไรรวดเดียวใน numpy นั้นถือเป็นการคำนวณที่มีประสิทธิภาพรวดเร็วกว่าการวนทำซ้ำ แต่ว่ากรณีที่ขนาดอาเรย์ใหญ่มากเกินนั้นผลจะตรงกันข้าม คือเจอคอขวดทำให้ช้าลงอย่างมาก บางครั้งอาจทำให้เครื่องค้างไปเลย มีความเสี่ยง
ดังนั้นจึงต้องคิดวิธีใหม่ที่จะแก้ปัญหาเมื่อเจอกับอาเรย์ขนาดใหญ่
วิธีการนั้นคือการแบ่งอาเรย์ออกเป็นท่อนๆแยกคำนวณ เขียนแก้ใหม่ได้ดังนี้
ในที่นี้ลองสร้างให้จำกัดขนาดอาเรย์อยู่ที่ประมาณล้านถ้าเป็นไปได้ เพียงแต่ว่าถ้าจำนวนข้อมูลเรียนรู้และจำนวนตัวแปรต้นคูณกันแล้วเกินล้านตั้งแต่แรกก็ช่วยไม่ได้อยู่ดี
ในกรณีนี้ตัวแปรมี 784 ตัว ดังนั้นแค่จำนวนข้อมูลเรียนรู้มีสัก 1300 ตัว ขนาดอาเรย์ก็เกินล้าน
ลองแยกข้อมูลทั้งหมดซึ่งมี 70000 ตัวออกมา 200 เป็นข้อมูลตรวจสอบ ส่วนที่เหลือใช้ในการฝึกทั้งหมด ส่วนจำนวนเพื่อนบ้านที่พิจารณาเลือกให้เป็น 1
เวลาที่ใช้จะค่อนข้างนาน และจะพบว่าผลการทำนายข้อมูลฝึกได้ 100% ซึ่งนั่นก็เป็นเรื่องแน่นอนสำหรับกรณีนี้ที่จำนวนเพื่อนบ้านเป็น 1 ส่วนผลการทำนายข้อมูลทดสอบเองก็ได้สูงถึง 97.5%
ทีนี้ลองดูว่าหากปรับจำนวนเพื่อนบ้านให้มากขึ้น ผลจะเป็นอย่างไร
คราวนี้ลองให้วนเปลี่ยนค่าจำนวนเพื่อนบ้านไปเรื่อยๆแล้วหาความแม่นยำเทียบดู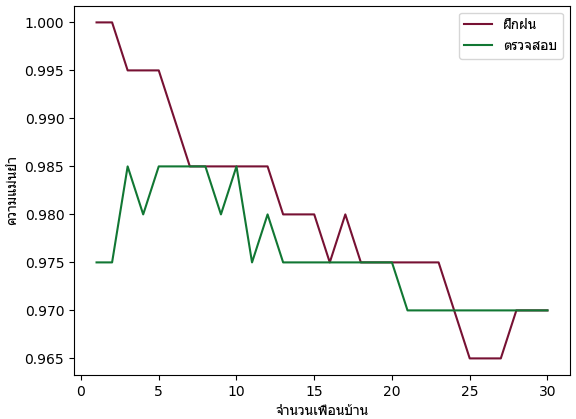
ผลที่ได้จะเห็นว่าที่จำนวนเพื่อนบ้านน้อยจะได้ผลออกมาค่อนข้างดี แม้ว่าจะเกิดการเรียนรู้เกินไปบ้างก็ตาม
โดยรวมแล้วก็เห็นได้ว่าวิธีพื้นฐานอย่างวิธีการเพื่อนบ้านใกล้สุด k ตัวก็สามารถทายข้อมูล MNIST ได้ถึงราวๆ 97~99% แล้ว ซึ่งสูงกว่าวิธีการวิเคราะห์ถดถอยโลจิสติกพอสมควร
สุดท้ายนี้ลองใช้ sklearn บ้าง ซึ่งก็เพิ่งได้แนะนำวิธีใช้ไปไปใน https://phyblas.hinaboshi.com/20171031
ดังที่ได้กล่าวไปแล้วว่าอัลกอริธึมของ sklearn นั้นทำให้การคำนวณเร็วกว่ามาก อีกทั้งเพื่อให้เร็วยิ่งขึ้นไปอีกสามารถใส่คีย์เวิร์ด n_jobs=-1 คือใช้ทุกคอร์ของ cpu ทำงานให้เต็มที่ เขียนโค้ดได้ดังนี้
จากนั้นวาดกราฟจะเห็นว่าได้ผลในลักษณะเดียวกัน แต่เร็วขึ้นมาก

ครั้งก่อนนั้นใช้วิธีการวิเคราะห์การถดถอยโลจิสติก แต่คราวนี้จะลองเปลี่ยนมาใช้วิธีการเพื่อนบ้านใกล้สุด k ตัว (KNN) ดูบ้าง
รายละเอียดเกี่ยวกับข้อมูลตัวเลข MNIST รวมถึงวิธีการดึงข้อมูลมาได้เขียนถึงไปในบทความนั้นแล้ว ในที่นี้จะไม่กล่าวถึงซ้ำอีก
สำหรับวิธีการเพื่อนบ้านใกล้สุด k ตัวนั้น ก่อนหน้านี้ได้เขียนวิธีการสร้างคลาสไปใน https://phyblas.hinaboshi.com/20171028
เพียงแต่ว่าหากนำมาใช้กับข้อมูล MNIST ทั้งๆอย่างนั้นเลยจะมีปัญหาได้ เพราะเนื่องจากขนาดของข้อมูลซึ่งมีขนาดใหญ่มาก จึงยังต้องมีการดัดแปลงอีกสักหน่อยเพื่อใช้
ข้อมูล MNIST มีจำนวนมิติมากถึง 784 และจำนวนภาพก็มากถึง 70000 ภาพ หมายความว่าอาเรย์มีขนาด 54880000
ในคลาสที่สร้างไว้นั้นมีขั้นตอนที่มีการสร้างอาเรย์ขนาดมหึมาขึ้น คือ X[None]-self.X[:,None]
ซึ่งหากใช้ข้อมูลทั้งหมด 70000 ภาพในการเรียนรู้ หมายความว่าอาเรย์นี้จะมีขนาด 70000×784×จำนวนภาพที่จะหาคำตอบ
ปกติการสร้างอาเรย์ขึ้นมาเพื่อคำนวณอะไรรวดเดียวใน numpy นั้นถือเป็นการคำนวณที่มีประสิทธิภาพรวดเร็วกว่าการวนทำซ้ำ แต่ว่ากรณีที่ขนาดอาเรย์ใหญ่มากเกินนั้นผลจะตรงกันข้าม คือเจอคอขวดทำให้ช้าลงอย่างมาก บางครั้งอาจทำให้เครื่องค้างไปเลย มีความเสี่ยง
ดังนั้นจึงต้องคิดวิธีใหม่ที่จะแก้ปัญหาเมื่อเจอกับอาเรย์ขนาดใหญ่
วิธีการนั้นคือการแบ่งอาเรย์ออกเป็นท่อนๆแยกคำนวณ เขียนแก้ใหม่ได้ดังนี้
import numpy as np
class Phueanban:
def __init__(self,nk=5):
self.nk = nk # จำนวนเพื่อนบ้านที่จะพิจารณา
def rianru(self,X,z):
self.X = X # เก็บข้อมูลตำแหน่ง
self.z = z # เก็บข้อมูลการแบ่งกลุ่ม
self.n_klum = z.max()+1 # จำนวนกลุ่ม
def thamnai(self,X):
n = len(X) # จำนวนข้อมูลที่จะคำนวณหา
n_batch = int(np.ceil(1000000./X.shape[1]/len(self.X)))
z = np.empty(n,dtype=int)
for c in range(0,n,n_batch):
Xn = X[c:c+n_batch]
n_Xn = len(Xn)
raya2 = ((Xn[None]-self.X[:,None])**2).sum(2)
klum_thi_klai = self.z[raya2.argsort(0)]
n_nai_klum = np.stack([(klum_thi_klai[:self.nk]==k).sum(0) for k in range(self.n_klum)])
mi_maksut = n_nai_klum.max(0)
maksutmai = (n_nai_klum==mi_maksut)
for i in range(n_Xn):
for j in range(self.nk):
k = klum_thi_klai[j,i]
if(maksutmai[k,i]):
z[i+c] = k
break
return zในที่นี้ลองสร้างให้จำกัดขนาดอาเรย์อยู่ที่ประมาณล้านถ้าเป็นไปได้ เพียงแต่ว่าถ้าจำนวนข้อมูลเรียนรู้และจำนวนตัวแปรต้นคูณกันแล้วเกินล้านตั้งแต่แรกก็ช่วยไม่ได้อยู่ดี
ในกรณีนี้ตัวแปรมี 784 ตัว ดังนั้นแค่จำนวนข้อมูลเรียนรู้มีสัก 1300 ตัว ขนาดอาเรย์ก็เกินล้าน
ลองแยกข้อมูลทั้งหมดซึ่งมี 70000 ตัวออกมา 200 เป็นข้อมูลตรวจสอบ ส่วนที่เหลือใช้ในการฝึกทั้งหมด ส่วนจำนวนเพื่อนบ้านที่พิจารณาเลือกให้เป็น 1
from sklearn import datasets
from sklearn.model_selection import train_test_split
mnist = datasets.fetch_openml('mnist_784')
X,z = mnist.data.astype(float),mnist.target.astype(int)
np.random.seed(0)
X_fuek,X_truat,z_fuek,z_truat = train_test_split(X,z,test_size=200/70000)
pb = Phueanban(nk=1)
pb.rianru(X_fuek,z_fuek)
zz = pb.thamnai(X_fuek[:200]) # ทำนายข้อมูลฝึก ดึงมาแค่ 200 ตัว ให้เท่ากับข้อมูลตรวจสอบ
print((zz==z_fuek[:200]).mean()) # ได้ 1.0
zz = pb.thamnai(X_truat) # ทำนายข้อมูลตรวจสอบ
print((zz==z_truat).mean()) # ได้ 0.975เวลาที่ใช้จะค่อนข้างนาน และจะพบว่าผลการทำนายข้อมูลฝึกได้ 100% ซึ่งนั่นก็เป็นเรื่องแน่นอนสำหรับกรณีนี้ที่จำนวนเพื่อนบ้านเป็น 1 ส่วนผลการทำนายข้อมูลทดสอบเองก็ได้สูงถึง 97.5%
ทีนี้ลองดูว่าหากปรับจำนวนเพื่อนบ้านให้มากขึ้น ผลจะเป็นอย่างไร
คราวนี้ลองให้วนเปลี่ยนค่าจำนวนเพื่อนบ้านไปเรื่อยๆแล้วหาความแม่นยำเทียบดู
import time
import matplotlib.pyplot as plt
pb = Phueanban()
pb.rianru(X_fuek,z_fuek)
maen_fuek = []
maen_truat = []
t1 = time.time()
for nk in range(1,31):
pb.nk = nk
zz = pb.thamnai(X_fuek[:200])
maen_fuek.append((zz==z_fuek[:200]).mean())
zz = pb.thamnai(X_truat)
maen_truat.append((zz==z_truat).mean())
# เนื่องจากใช้เวลานาน ให้จับเวลาแล้วแสดงความคืบหน้าไปด้วยเพื่อไม่ให้เคว้ง
print(u'รอบที่ %d เวลาผ่านไปแล้ว %.2f วินาที'%(nk,time.time()-t1))
plt.plot(np.arange(1,31),maen_fuek,'#771133')
plt.plot(np.arange(1,31),maen_truat,'#117733')
plt.xlabel(u'จำนวนเพื่อนบ้าน',family='Tahoma')
plt.ylabel(u'ความแม่นยำ',family='Tahoma')
plt.legend([u'ฝึกฝน',u'ตรวจสอบ'],prop={'family':'Tahoma'})
plt.show()
ผลที่ได้จะเห็นว่าที่จำนวนเพื่อนบ้านน้อยจะได้ผลออกมาค่อนข้างดี แม้ว่าจะเกิดการเรียนรู้เกินไปบ้างก็ตาม
โดยรวมแล้วก็เห็นได้ว่าวิธีพื้นฐานอย่างวิธีการเพื่อนบ้านใกล้สุด k ตัวก็สามารถทายข้อมูล MNIST ได้ถึงราวๆ 97~99% แล้ว ซึ่งสูงกว่าวิธีการวิเคราะห์ถดถอยโลจิสติกพอสมควร
สุดท้ายนี้ลองใช้ sklearn บ้าง ซึ่งก็เพิ่งได้แนะนำวิธีใช้ไปไปใน https://phyblas.hinaboshi.com/20171031
ดังที่ได้กล่าวไปแล้วว่าอัลกอริธึมของ sklearn นั้นทำให้การคำนวณเร็วกว่ามาก อีกทั้งเพื่อให้เร็วยิ่งขึ้นไปอีกสามารถใส่คีย์เวิร์ด n_jobs=-1 คือใช้ทุกคอร์ของ cpu ทำงานให้เต็มที่ เขียนโค้ดได้ดังนี้
from sklearn.neighbors import KNeighborsClassifier as Knn
knn = Knn(n_jobs=-1)
knn.fit(X_fuek,z_fuek)
maen_fuek = []
maen_truat = []
for i in range(1,31):
knn.set_params(n_neighbors=i)
maen_fuek.append(knn.score(X_fuek[:200],z_fuek[:200]))
maen_truat.append(knn.score(X_truat,z_truat))จากนั้นวาดกราฟจะเห็นว่าได้ผลในลักษณะเดียวกัน แต่เร็วขึ้นมาก
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib