วิเคราะห์และสรุปสถิติของดาวเคราะห์นอกระบบสุริยะทั้งหมดที่ค้นพบในยุคเฮย์เซย์
เขียนเมื่อ 2019/05/02 16:02
แก้ไขล่าสุด 2022/07/19 04:38
ที่ญี่ปุ่นเพิ่งจะเปลี่ยนศักราชใหม่ไป ยุคเฮย์เซย์ (平成) ที่ยาวนานมาตั้งแต่ปี 1989 ถึง 30 เมษายน 2019 รวมเวลาสามสิบปี ตั้งแต่ 1 พฤษภาเป็นต้นมาเข้าสู่ยุคเรย์วะ (令和)
เนื่องในโอกาสนี้เลยอยากจะสรุปเกี่ยวกับดาวเคราะห์นอกระบบสุริยะ (太陽系外惑星) ทั้งหมดที่มีการค้นพบในช่วงตลอดเวลาที่ผ่านมานี้สักหน่อย
ดาวเคราะห์นอกระบบสุริยะก็คือดาวเคราะห์นอกเหนือจากดาวเคราะห์ ๘ ดวงที่พวกเรารู้จักกันดี คือ ดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัส ดาวเสาร์ ดาวยูเรนัส ดาวเนปจูน (เมื่อก่อนรวมดาวพลูโตด้วยเป็น ๙ ดวง)
มนุษย์มองดูดาวมาตั้งแต่อดีต ตั้งแต่รู้ว่าดวงอาทิตย์แท้จริงก็เป็นแค่ดาวฤกษ์ดวงหนึ่งเหมือนกับดาวนับล้านที่อยู่บนฟ้าก็ย่อมมีความคิดว่ารอบๆดาวเหล่านั้นเองก็อาจมีดาวเคราะห์โคจรอยู่ด้วยเช่นกัน
ความพยายามในการค้นหาดาวเคราะห์นอกระบบสุริยะนั้นมีมาตั้งแต่อดีต แต่เพิ่งจะยืนยันการค้นพบแน่นอนได้ในปี 1995
จนถึงตอนนี้ซึ่งเพิ่งสิ้นสุดยุคเฮย์เซย์ไป จำนวนดาวเคราะห์นอกระบบสุริยะที่ค้นพบแล้วมีทั้งหมดประมาณ ๔๐๐๐ ดวง
สำหรับในบทความนี้จะเขียนโปรแกรมภาษาไพธอน โดยใช้มอดูล pandas และ matplotlib เป็นหลัก เพื่อวิเคราะห์ข้อมูลของดาวเคราะห์เหล่านั้น
บทความนี้เริ่มแรกเขียนเป็นภาษาญี่ปุ่นลงในบล็อก qiita https://qiita.com/phyblas/items/ec29c49302c7b0a60905
เนื้อหาที่ลงตรงนี้เป็นการเรียบเรียงใหม่เป็นภาษาไทย
สารบัญ
การดึงข้อมูลมาใช้
ข้อมูลดาวเคราะห์นั้นสามารถดูได้จากเว็บไซต์ต่างๆ จะโหลดมาก็ได้ แต่ถ้าใช้มอดูลในไพธอนมีวิธีที่จะดึงข้อมูลดาราศาสตร์มาง่ายๆโดยไม่ต้องไปโหลดจากเว็บเอง
มอดูลนั้นชื่อว่า astroquery เป็นมอดูลลูกของมอดูล astropy ที่ใช้กันกว้างขวางในวงการดาราศาสตร์
สามารถลงได้ง่ายด้วย pip หรือ conda
ที่จะใช้ตรงนี้คือฐานข้อมูล NasaExoplanetArchive เป็นฐานข้อมูลที่เก็บข้อมูลของดาวเคราะห์นอกระบบสุริยะเอาไว้
รายละเอียดอ่านได้ในเว็บ https://exoplanetarchive.ipac.caltech.edu/index.html
จากเว็บนี้จะค้นข้อมูลของดาวเคราะห์หรือโหลดมาก็ได้ แต่ถ้าใช้ astroquery ก็จะโหลดข้อมูลเข้ามาในโปรแกรมไพธอนแล้วใช้วิเคราะห์ได้ทันที ไม่ต้องไปโหลดจากเว็บมาเองก่อน
เมื่อใช้คำสั่ง get_confirmed_planets_table แล้วก็จะได้ข้อมูลเป็นตารางมาอย่างที่เห็น
จากตารางจะพบว่ามีดาวเคราะห์นอกระบบที่ยืนยันแล้วทั้งหมด ๓๙๔๖ ดวง
ข้อมูลนี้เป็นส่วนที่ลงในเว็บแล้วเท่านั้น อาจยังมีส่วนที่ไม่ได้ลง และข้อมูลจากเว็บต่างๆก็อาจไม่เหมือนกัน เช่นอีกเว็บคือ http://exoplanet.eu มักจะมีข้อมูลมากกว่า
ในที่นี้จะใช้ข้อมูล NasaExoplanetArchive ที่โหลดมาตอนขึ้นยุคเรย์วะพอดี คือเที่ยงคืนกว่าของวันที่ 1 พฤษภาคม ตามเวลาญี่ปุ่น
เมื่อใช้คำสั่งดึงข้อมูลนี้ไปแล้วข้อมูลก็จะถูกโหลดเข้ามา เวลาที่ใช้ครั้งต่อไปข้อมูลจะไม่มีการโหลดใหม่ แต่ไปใช้ข้อมูลที่เก็บไว้ในเครื่อง ทำให้ใช้งานได้เร็วขึ้น เพียงแต่ปัญหาคือข้อมูลพวกนี้มีการเพิ่มเติมเปลี่ยนแปลงอยู่สม่ำเสมอ ดังนั้นควรจะโหลดใหม่เรื่อยๆดีกว่า
เพื่อที่จะให้โหลดใหม่ทุกครั้ง ให้เติม cache=0 ลงไปด้วย
ตารางข้อมูลที่ได้มานี้เป็นออบเจ็กต์ชนิด QTable ของ astropy ซึ่งถ้าไม่คุ้นเคยก็อาจใช้งานได้ไม่สะดวก ดังนั้นเพื่อให้ใช้งานคล่องจะเปลี่ยนเป็นข้อมูล DataFrame ของ pandas
ข้อมูลมี ๘๔ สดมภ์ (column) แต่ในที่นี้จะดึงสดมภ์ pl_name ซึ่งเก็บชื่อของดาวเคราะห์มาใช้เป็นดัชนี เหลือ ๘๓ สดมภ์
คำอธิบายของแต่ละสดมภ์มีเขียนไว้ใน https://exoplanetarchive.ipac.caltech.edu/docs/API_exoplanet_columns.html
จากนี้ไปจะใช้ข้อมูลจากตารางนี้เพื่อมาวิเคราะห์
วิธีการค้นหา
ก่อนอื่น หลายคนคงสงสัยว่าเราจะหาดาวเคราะห์ที่อยู่ไกลขนาดนั้นได้อย่างไร
วิธีการค้นหาดาวเคราะห์นอกระบบนั้นมีอยู่หลากหลาย ภายในข้อมูลนี้มีการบอกด้วยว่าดาวเคราะห์ดวงนั้นใช้วิธีการไหนค้นหา เขียนเอาไว้ในสดมภ์ pl_discmethod ลองดึงมาเขียนแผนภูมิแท่งสรุปกันดู
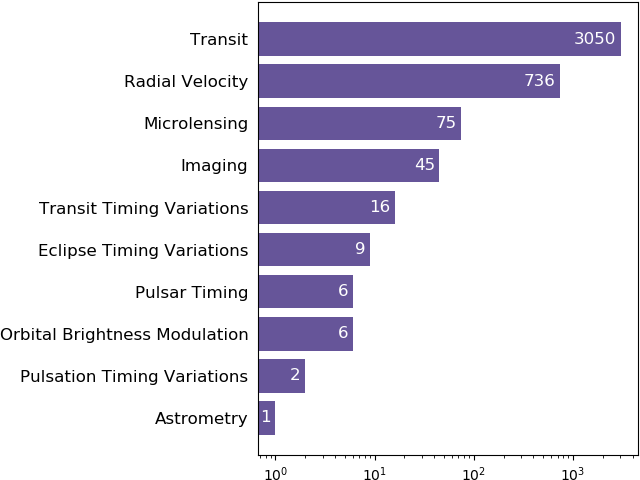
จะเห็นว่าภายในข้อมูลนี้มีอยู่ทั้งหมด ๑๐ วิธีการ ชื่อแต่ละวิธีหากเทียบแปลเป็นไทยก็จะเป็นดังนี้
Transit = การเคลื่อนผ่าน
Radial Velocity = ความเร็วแนวเล็ง
Microlensing = ไมโครเลนส์โน้มถ่วง
Imaging = การถ่ายภาพโดยตรง
Transit Timing Variation = ความแปรปรวนของเวลาเคลื่อนผ่าน
Eclipse Timing Variations = ความแปรปรวนของเวลาเกิดคราส
Pulsar Timing = การจับเวลาพัลซาร์
Orbital Brightness Modulation = การผันผวนของความสว่างวงโคจร
Pulsar Timing Variations = ความแปรปรวนของการจับเวลาพัลซาร์
Astrometry = มาตรดาราศาสตร์
รายละเอียดเกี่ยวกับแต่ละวิธีสามารถค้นได้ตามเว็บต่างๆ ในที่นี้จึงขอละไว้ ขอนำวิกิมาใช้อ้างอิง https://th.wikipedia.org/wiki/วิธีตรวจจับดาวเคราะห์นอกระบบ
อุปกรณ์สังเกตการณ์
มีกล้องโทรทรรศน์หรือหอดูดาวหลายแห่งที่ใช้ในการค้นพบดาวเคราะห์นอกระบบได้ ไม่ว่าจะเป็นกล้องโทรทรรศน์จากหอดูดาวบนพื้นโลก หรือกล้องโทรทรรศน์ที่ถูกส่งขึ้นไปในอวกาศ
ข้อมูลที่บอกว่าดาวเคราะห์ดวงนั้นๆถูกค้นพบด้วยเครื่องมือไหนก็ได้ใส่ไว้ในฐานข้อมูลนี้ด้วย อยู่ในสดมภ์ pl_facility ลองมาดูกัน
ดูแล้วก็จะเห็นได้ว่าที่ค้นพบมานี้เกินกว่าครึ่งเป็นผลงานของกล้องเคพเลอร์ (Kepler)
กล้องเคพเลอร์ หรือชื่อเต็มว่ากล้องโทรทรรศน์อวกาศเคพเลอร์ (Kepler space telescope) เป็นกล้องโทรทรรศน์ที่ถูกส่งขึ้นไปในอวกาศตั้งแต่ปี 2009 เพื่อค้นหาดาวเคราะห์ด้วยวิธีการเคลื่อนผ่าน และปลดประจำการในปี 2018
ตั้งแต่ปี 2009 ถึง 2013 กล้องเคพเลอร์ทำการสังเกตการณ์ด้วยสภาพที่สมบูรณ์เต็มที่ แต่หลังจากนั้นล้อปฏิกิริยา (reaction wheel) เกิดชำรุดขึ้นเป็นอันที่ ๒ ตั้งแต่ปี 2014 จึงเปลี่ยนชื่อเรียกเป็น K2 แล้วทำการสังเกตการณ์ต่อไปในสภาพที่ด้อยลงกว่าเดิม
ในฐานข้อมูลนี้ที่เขียนว่า Kepler หมายถึงกล้องเคพเลอร์ช่วงปี 2009 ถึง 2013 แต่ถ้าเป็นกล้องเคพเลอร์ในช่วงที่ใช้ชื่อว่า K2 ก็จะเขียนว่า K2 แยกกัน
K2 นั้นด้อยลงว่ากล้องเคพเลอร์ตอนช่วงแรก แต่ก็ยังค้นพบดาวเคราะห์ได้มากมายเช่นกัน
ดาวเทียมสำรวจดาวเคราะห์นอกระบบ Transiting Exoplanet Survey Satellite (TESS) เป็นผู้สืบทอดของกล้องเคพเลอร์ จะทำการสังเกตการณ์ค้นหาดาวเคราะห์ด้วยวิธีการเคลื่อนผ่านเช่นกัน
สำหรับหอดูดาวภาคพื้นดินที่สร้างผลงานมากที่สุดก็คือ หอดูดาวลาซียา (La Silla Observatory) ที่ทะเลทรายอาตากามา ประเทศชิลี
มีไม่น้อยที่ใช้กล้องโทรทรรศน์จากหลายแห่งร่วมกันในการค้นพบ
ส่วนของญี่ปุ่นก็มีหอดูดาวโอกายามะ (岡山天体物理観測所) ค้นหาดาวเคราะห์ด้วยวิธีความเร็วแนวเล็ง
นอกจากนี้ยังมีกล้องโทรทรรศน์สึบารุ (すばる望遠鏡) อยู่ที่ฮาวายแต่ก็เป็นของญี่ปุ่น ใช้ทั้งวิธีความเร็วแนวเล็ง และวิธีการถ่ายภาพโดยตรง ในการค้นหาดาวเคราะห์
ขนาดของดาวเคราะห์
ขนาดของดาวเคราะห์ถูกเขียนไว้ที่สดมภ์ pl_radj ส่วนขนาดของดาวฤกษ์ที่เป็นดาวหลักอยู่ที่สดมภ์ st_rad
เพียงแต่หน่วยที่ใช้จะต่างกัน ขนาดดาวเคราะห์ใช้หน่วยเป็นจำนวนเท่าของดาวพฤหัส ส่วนของดาวหลักใช้เป็นจำนวนเท่าของดวงอาทิตย์
เนื่องจากใช้หน่วยเป็นจำนวนเท่า ขนาดที่ว่านี้อาจหมายถึงรัศมีหรือเส้นผ่านศูนย์กลางก็ได้ มีความหมายไม่ต่างกัน
ยังมีดาวเคราะห์บางดวงที่ไม่ได้ถูกวัดขนาด ซึ่งส่วนที่ไม่มีข้อมูลนั้นจะถูกเขียนเป็น 0 ไป ดังนั้นก่อนที่จะวิเคราะห์ข้อมูลขนาดควรจะต้องตัดส่วนนั้นทิ้งก่อน
จากข้อมูลจะเห็นได้ว่าจากดาวทั้ง ๓๙๔๖ ดวง มีอยู่แค่ ๓๐๘๐ ดวงที่รู้ขนาด ส่วนที่เหลือไม่มีข้อมูล
ดาวที่หาเจอด้วยวิธีการความเร็วแนวเล็งและไมโครเลนส์โน้มถ่วงนั้นปกติจะไม่สามารถรู้ขนาดของดาวเคราะห์ได้
สำหรับดาวที่ค้นพบด้วยวิธีความเร็วแนวเล็งนั้นอาจจะสังเกตการณ์ด้วยวิธีอื่นเพื่อหาขนาดได้ จึงมีบางส่วนที่รู้ขนาด แต่สำหรับดาวที่ค้นพบด้วยวิธีไมโครเลนส์โน้มถ่วงนั้นจะสังเกตการณ์ซ้ำด้วยวิธีอื่นได้ยาก จึงไม่มีดวงไหนที่รู้ขนาดเลย
ลองดูจำนวนดาวเคราะห์ที่ค้นพบด้วยวิธีต่างๆเฉพาะที่รู้รัศมี
ลองดูดาวที่เล็กและใหญ่ที่สุด
ขนาดใหญ่สุดใหญ่ถึง ๖.๙ เท่าของดาวพฤหัส ดาวที่ใหญ่กว่าดาวพฤหัสมีอยู่ไม่น้อย แต่ก็มีขีดจำกัดอยู่ เพราะถ้าใหญ่เกินไปอาจถูกมองว่าเป็นดาวแคระน้ำตาล (褐色矮星) ได้
ดาวแคระน้ำตาลคือดาวฤกษ์ชนิดที่มีขนาดเล็กที่สุด มักสับสนกับดาวเคราะห์ขนาดใหญ่ได้ง่าย
โลกมีขนาดเป็น ๐.๐๘๙๒๑ เท่าของดาวพฤหัส ดาวที่เล็กที่สุดคือ Kepler-37 b มีขนาดเป็น ๐.๐๓ เท่าของดาวพฤหัส นั่นคือ ๐.๓๕๔ เท่าของโลก
ดาวเคราะห์ที่เล็กที่สุดในระบบสุริยะคือดาวพุธซึ่งมีขนาด ๐.๓๘๓ เท่าของโลก ดาวเคราะห์ที่เล็กกว่าดาวพุธเท่าที่พบมาจนถึงตอนนี้มีแค่ Kepler-37 b นี้เท่านั้น
ดาวเคราะห์ที่เล็กกว่าโลกที่ค้นพบแล้วก็มีอยู่ไม่น้อย ลองดูว่ามีกี่ดวงที่ใหญ่กว่าดาวพฤหัสและเล็กกว่าโลก
ลองดูการแจกแจงขนาดดาวเคราะห์
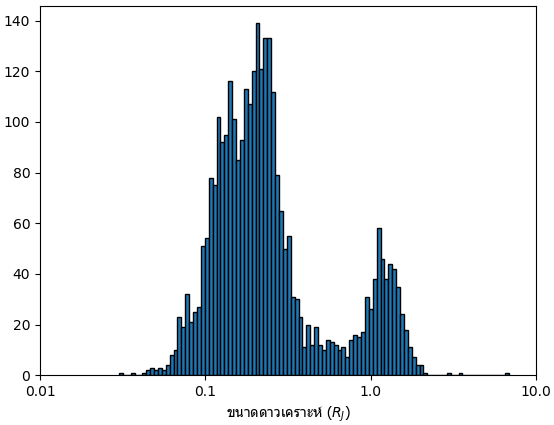
ขนาดของดาวหลัก
ต่อไปดูขนาดของดาวฤกษ์ที่เป็นดาวหลักของดาวเคราะห์
การแจกแจงขนาดดาวหลัก
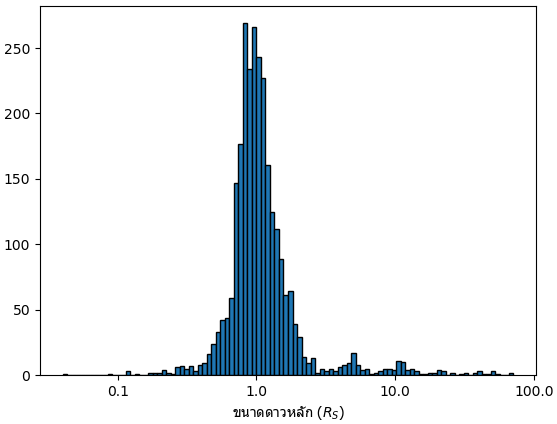
ขนาดของดาวเคราะห์เทียบกับดาวหลัก
ต่อไปมาเปรียบเทียบขนาดของดาวเคราะห์และดาวหลักดู แต่ก่อนอื่นต้องเปลี่ยนหน่วยให้เท่ากันก่อน
ขนาดของดาวพฤหัสเป็น ๐.๑๐๐๔๙ เท่าของดวงอาทิตย์
ดาวเคราะห์ที่อัตราส่วนขนาดต่อดาวหลักสูงสุดนั้นอัตราส่วนสูงกว่า ๑ นั่นหมายความว่าใหญ่ยิ่งกว่าดาวหลักเสียอีก ที่จริงดาวนั้นไม่ได้ใหญ่เป็นพิเศษ แค่ดาวหลักเป็นดาวแคระน้ำตาลซึ่งมีขนาดเล็กมากเท่านั้น
จากนั้นมาดูการแจกแจงของขนาดดาวเคราะห์และดาวหลัก ในที่นี้จะใส่โลกกับดาวพฤหัสลงไปด้วยเพื่อเปรียบเทียบ
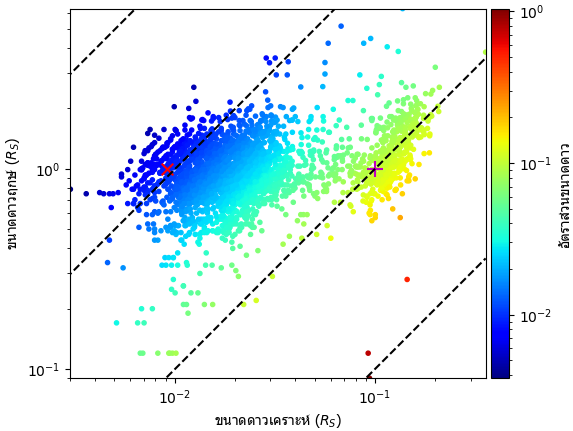
× ทางซ้ายคือโลก ส่วน + ทางขวาคือดาวพฤหัส
ดูแล้วจะเห็นว่าน่าสนใจตรงที่ขนาดของดาวเคราะห์หลักๆแบ่งออกเป็น ๒ กลุ่มก้อนใหญ่ คือกลุ่มที่ใกล้เคียงโลกและกลุ่มที่ใกล้เคียงดาวพฤหัส
คาบการโคจรของดาวเคราะห์
คาบการโคจรของดาวเคราะห์เขียนอยู่ที่สดมภ์ pl_orbper หน่วยเป็นวัน
ดูการกระจาย
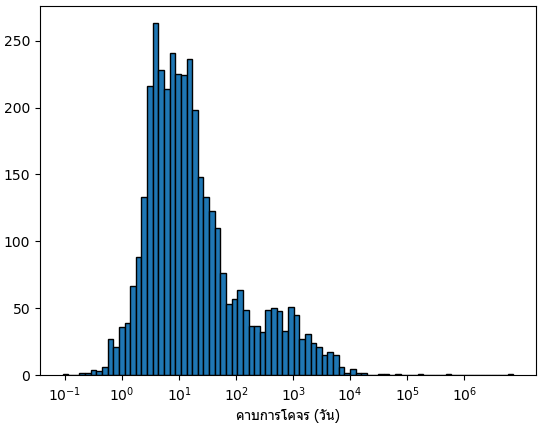
ยิ่งคาบการโคจรสั้นก็หมายความว่าดาวเคราะห์จะเคลื่อนผ่านดาวหลักบ่อยขึ้น ยิ่งอยู่ใกล้ผลของแรงโน้มถ่วงก็ยิ่งมาก ดังนั้นดาวเคราะห์ที่คาบวงโคจรสั้นจึงหาง่ายทั้งด้วยวิธีความเร็วแนวแล็งและวิธีการเคลื่อนผ่าน
ในระบบสุริยะดาวเคราะห์ที่อยู่ใกล้สุดคือดาวพุธซึ่งมีคาบการโคจร ๘๗.๙๖๙ วัน นั่นแสดงว่าดาวเคราะห์ส่วนใหญ่ที่ค้นพบมาแล้วนั้นมีขนาดวงโคจรอยู่ในระดับที่แคบกว่ามาตรฐานของระบบสุริยะ
นี่อาจเป็นผลจากความโน้มเอียงในการค้นหา แต่ก็ทำให้รู้ว่ามีระบบดาวเคราะห์ที่ต่างไปจากระบบสุริยะมากแบบนี้อยู่ไม่น้อย
ลองเทียบขนาดดาวเคราะห์และคาบวงโคจรของดาวเคราะห์ที่ค้นพบด้วยวิธีต่างๆดู
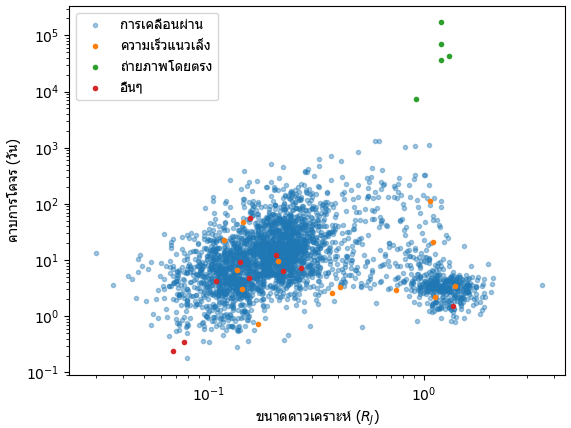
จะเห็นว่าดาวเคราะห์ที่พบด้วยวิธีความเร็วแนวเล็งและวิธีการเคลื่อนผ่านจะมีคาบสั้น แต่ดาวที่พบจากการถ่ายภาพโดยตรงจะมีขนาดใหญ่และคาบยาว
มุมเอียงวงโคจรของดาวเคราะห์
มุมเอียงวงโคจรของดาวเคราะห์เมื่อมองจากโลกเขียนอยู่ในสดมภ์ pl_orbincl แต่ที่มีข้อมูลมีอยู่ไม่มาก
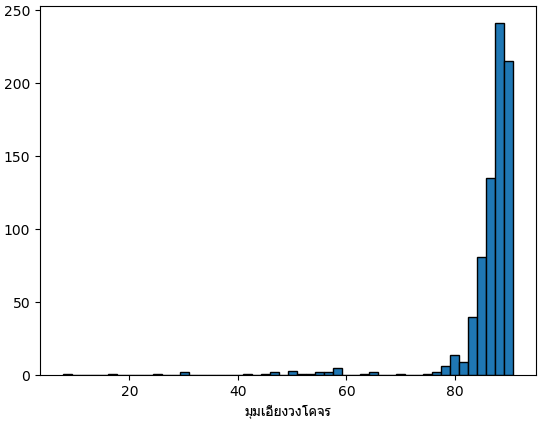
ถ้าวงโคจรตั้งฉากกับมุมมองจากโลกก็จะเจอด้วยวิธีการเคลื่อนผ่านได้ง่าย ดังนั้นดาวเคราะห์ส่วนใหญ่ที่ค้นพบจึงมีมุมเอียงวงโคจรอยู่ที่ประมาณ ๘๐-๙๐ ซะมาก
มวลของดาวเคราะห์
มวลของดาวเคราะห์เขียนอยู่ที่สดมภ์ pl_bmassj หน่วยเป็นจำนวนเท่าของดาวพฤหัส
แต่ว่าข้อมูลส่วนหนึ่งในนี้ไม่ใช่มวลที่แท้จริง แต่เป็นแค่มวลขั้นต่ำ ซึ่งหมายถึง Msin(i)
โดยที่ i คือมุมเอียงวงโคจรเทียบกับโลก ส่วน M คือมวลจริงๆ
ที่เป็นแบบนี้เพราะว่าดาวเคราะห์ที่ค้นพบโดยวิธีความเร็วเชิงมุมจะวัดมวลโดยดูจากขนาดของสเปกตรัมที่เปลี่ยนแปลงจากปรากฏการณ์ดอพเลอร์ที่เกิดขึ้น ซึ่งความเปลี่ยนแปลงขึ้นอยู่กับมวล แต่ก็ขึ้นอยู่กับมุมเอียงที่ทำกับโลกด้วย
ดังนั้นค่าที่วัดได้จึงอยู่ในรูปของ Msin(i) คือถ้ามุมเอียงมากหมายความว่ามวลจริงๆจะมากกว่าค่านั้นมาก
หากดูที่สดมภ์ pl_bmassprov อันที่มวลแสดงเป็นค่ามวลขั้นต่ำจะเขียนว่า Msini
ดาวเคราะห์ที่ค้นพบด้วยวิธีความเร็วแนวเล็งหากไม่รู้มุมเอียงวงโคจรก็จะไม่รู้มวลที่แท้จริง รู้ได้แค่มวลขั้นต่ำ แต่ถ้ารู้มุมเอียงแล้วในสดมภ์ pl_bmassprov จะเขียนว่า Msin(i)/sin(i) แล้วค่ามวลก็จะถูกเขียนเป็นมวลจริงไว้แล้ว
หากมวลถูกวัดด้วยวิธีอื่น ใน pl_bmassprov จะเขียนว่า Mass เฉยๆ
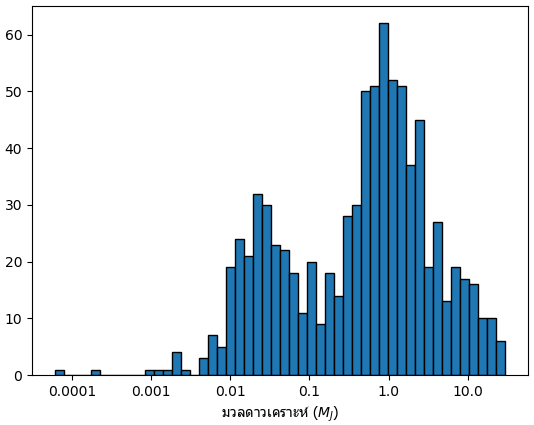
ลองมาดูการกระจายของมวลดาวเคราะห์เฉพาะที่รู้มวลแน่นอนแล้ว
มวลของดาวหลัก
มวลของดาวหลักเขียนอยู่ที่สดมภ์ st_mass หน่วยเป็นจำนวนเท่าของมวลดวงอาทิตย์
ดาวหลักที่มวลใกล้เคียงกับดวงอาทิตย์จะมีค่อนข้างเยอะ
ความหนาแน่นของดาวเคราะห์
ค่าความหนานแน่นของดาวเคราะห์อยู่ที่สดมภ์ pl_dens หน่วยคือกรัมต่อลูกบาศก์เมตร แต่ที่มีข้อมูลมีอยู่น้อย และความไม่แน่นอนก็สูงด้วย
ความคลาดเคลื่อนของความหนาแน่นดูได้ที่สดมภ์ pl_denserr1 และ pl_denserr2
ดาวที่มีความหนาแน่นมากที่สุดหนาแน่นถึง ๗๗.๗ g/cm3 แต่ก็มี ±๕๕ จึงมีความไม่แน่นอนมาก
ตำแหน่งบนทรงกลมท้องฟ้า
ค่าไรต์แอสเซนชัน (right ascention) และเดคลิเนชัน (declination) ซึ่งบอกตำแหน่งของดาวบนพิกัดทรงกลมท้องฟ้านั้นอยู่ในสดมภ์ ra และ dec หน่วยเป็นองศา
หากมองดูบนท้องฟ้าจะเห็นว่าตรงไหนก็เห็นดาวได้หมด การค้นหาดาวเคราะห์ก็ทำกับดาวทั่วท้องฟ้า แต่ว่าก็มีความโน้มเอียงในการค้นหาอยู่ ขึ้นอยู่กับวิธีการ
ลองดูการกระจายของตำแหน่งโดยแยกแต่ละวิธี
ดาวที่ค้นหาด้วยวิธีความเร็วแนวเล็งนั้นค่อนข้างกระจายสม่ำเสมอ แต่ที่หาด้วยวิธีการเคลื่อนผ่านกับวิธีไมโครเลนส์โน้มถ่วงจะรวมกันแน่นอยู่มากที่บางจุด
สาเหตุเป็นเพราะวิธีการไมโครเลนส์โน้มถ่วงนั้นจะได้ผลดีมากเฉพาะกับแถวใจกลางดาราจักรทางช้างเผือกซึ่งมีดาวอยู่หนาแน่นใช้เป็นฉากหลังได้
ส่วนวิธีการเคลื่อนผ่านนั้นที่จริงไม่ได้มีความแตกต่างมากถึงขนาดนั้น เพียงแต่ว่ากล้องเคพเลอร์นั้นได้ทำการค้นหาดาวเคราะห์อยู่แค่ที่บริเวณเล็กๆที่จำกัดไว้เท่านั้น จึงทำให้ดาวที่ค้นพบกระจุกอยู่ตรงนั้น
เคพเลอร์ในช่วงต้นจะส่งไปแค่บริเวณเล็กๆในกลุ่มดาวหงส์เท่านั้น ส่วนตอนที่เป็น K2 เปลี่ยนเป็นส่องไปรอบๆบริเวณใกล้ๆแนวสุริยวิถี
ในข้อมูลนี้มีสดมภ์ pl_kepflag และ pl_k2flag ซึ่งบอกว่าดาวเคราะห์ดวงนั้นอยู่ในเป้าหมายสังเกตการณ์ของเคพเลอร์หรือ K2 หรือไม่ (0=ไม่, 1=ใช่)
ดาวในกลุ่มนี้จะกระจายอยู่แค่ในบริเวณจำกัดเท่านั้น
นั่นหมายความว่าดาวเกินกว่าครึ่งที่ค้นพบไปนั้นอยู่ในกลุ่มดาวหงส์ซึ่งเป็นเป้าหมายการสังเกตการณ์ของกล้องเคพเลอร์เท่านั้นเอง
หากลองเอาดาวที่เป็นเป้าหมายของเคพเลอร์และที่หาด้วยไมโครเลนส์โน้มถ่วงออกไปก็จะไม่มีบริเวณไหนที่กระจุกกันแน่นเป็นพิเศษอีก
อาจลองแปลงจากไรต์แอสเซนชันและเดคลิเนชันไปเป็นทรงกลมท้องฟ้าในสามมิติดูการแจกแจงได้
ในที่นี้สีฟ้าและสีเทาคือดาวที่เป็นเป้าหมายของเคพเลอร์และ K2 ส่วนสีแดงคือที่ค้นด้วยวิธีไมโครเลนส์โน้มถ่วง
ระยะห่างจากโลก
ระยะห่างของระบบดาวเคราะห์นั้นจากโลกเขียนไว้ในสดมภ์ st_dist หน่วยเป็น pc
พื้นที่ของทรงกลมแปรตามกำลังสองของรัศมี ดังนั้นยิ่งไกลยิ่งมีดาวมาก แต่ถ้าไกลไปก็จะเห็นได้ยาก ดังนั้นจึงเจอมากสุดแถวๆ ๑๐๐๐ pc
หากนำระยะห่างมาคำนวณเข้ากับไรต์แอสเซนชันและเดคลิเนชันก็จะแสดงการกระจายในปริภูมิสามมิติได้
ส่วนใหญ่จะอยู่ใน ๑๐๐๐ pc แต่ทางฝั่งหันไปทางใจกลางดาราจักรทางช้างเผือกนั้นมีดาวที่ค้นพบด้วยวิธีไมโครเลนส์โน้มถ่วงกระจัดกระจายอยู่มาก
ความสว่างของดาวหลัก
โชติมาตร (magnitude) หรือ อันดับความสว่าง เป็นค่าที่บอกถึงความสว่างของดาว ค่านี้ยิ่งน้อยยิ่งหมายถึงสว่างมาก
โชติมาตรของดาวหลักเขียนไว้ในสดมภ์ st_optmag
ดาวที่โชติมาตรต่ำส่วนใหญ่เป็นดาวที่เป็นที่รู้จักดี
ดาวทั้ง ๖ นี้คือ
- อัลเดบาราน (Aldebaran) = α กลุ่มดาววัว
- ปอลลุกซ์ (Pollux) = β กลุ่มดาวคนคู่
- ฟอมาลเฮาต์ (Fomalhaut) = α กลุ่มดาวปลาทางใต้
- γ กลุ่มดาวสิงโต
- α กลุ่มดาวแกะ
- β กลุ่มดาวหมีเล็ก
โชติมาตรนี้เป็นโชติมาตรปรากฏที่มองจากโลก ซึ่งยิ่งไกลก็จะยิ่งเห็นมืดลง
ลองดูความสัมพันธ์ระหว่างขนาดดาวกับระยะทางจากโลกและโชติมาตร
ถ้าจะแปลงเป็นโชติมาตรสัมบูรณ์ซึ่งแสดงความสว่างจริงของดาวก็คำนวณโดย
โชติมาตรสัมบูรณ์ = โชติมาตรปรากฏ + 5 - 5 log10(ระยะห่าง)
ลองคำนวณโชติมาตรสัมบูรณ์แล้วดูการแจกแจงดู
อุณหภูมิยังผลของดาวหลัก
ค่าอุณหภูมิยังผลของดาวหลักเขียนไว้ที่สดมภ์ st_teff หน่วยเป็นเคลวิน
จะเห็นว่าดาวที่ร้อนที่สุดนั้นร้อนถึง ๕๗๐๐๐ เคลวิน แต่ว่าดาวนั้นค่อนข้างพิเศษ ที่จะร้อนขนาดนั้นมีไม่มาก ส่วนใหญ่จะอยู่ที่ ๕๐๐๐~๖๐๐๐ ใกล้เคียงดวงอาทิตย์
ลองดูชื่อดาวที่ร้อนเป็นพิเศษพวกนี้ดู
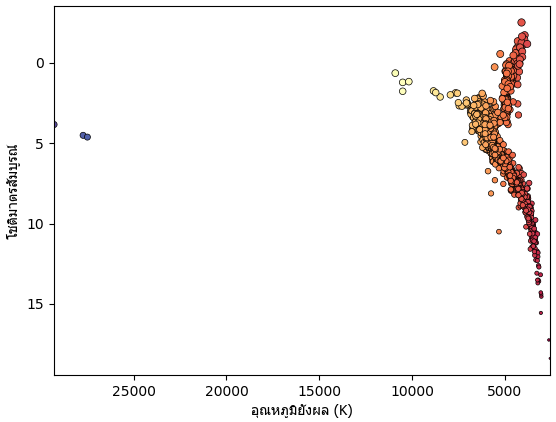
ถ้านำอุณหภูมิยังผลและโชติมาตรสัมบูรณ์มาวาดกราฟก็จะได้แผนภาพแฮร์ทสชปรุง-รัสเซล
จำนวนดาวเคราะห์ในระบบ
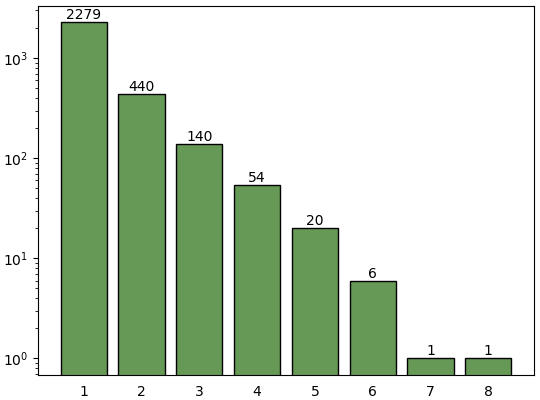
จำนวนดาวเคราะห์ทั้งหมดที่ถูกค้นพบแล้วในแต่ละระบบถูกเขียนไว้ที่สดมภ์ pl_pnum
ลองมาดูกันว่าแต่ละระบบมีการค้นพบดาวกันมากแค่ไหนแล้ว
ดูแล้วที่พบมากสุดคือ ๘ ดวง เท่ากับระบบสุริยะเลย
ลองดูชื่อของระบบที่มี ๗ และ ๘ ดวงนี้ดู
ระบบ ๘ ดวงนี้ชื่อ KOI-351 หรืออีกชื่อคือ Kepler-90 ซึ่งที่จริงแล้วเคยเขียนแนะนำไปในบทความก่อนหน้านี้ ว่าถูกค้นพบโดยปัญญาประดิษฐ์
อ่านได้ที่ https://phyblas.hinaboshi.com/20171216
ส่วนระบบที่มี ๗ ดวงคือ TRAPPIST-1 ซึ่งค้นพบโดยกล้องโทรทรรศน์ TRAPPIST ที่หอดูดาวลาซียา
น่าลองมาดูว่าดาวแบบไหนที่เจอดาวเคราะห์ได้มาก ลองดูสมบัติต่างๆของดาวที่มีดาวเคราะห์ถึง ๕ ดวงขึ้นไปกัน
KOI-351 (Kepler-90) นั้นเป็นดาวที่ค่อนข้างใกล้เคียงกับดวงอาทิตย์ แต่ TRAPPIST-1 นั้นค่อนข้างมืดและเล็กมาก
ลองดูความสัมพันธ์ระหว่างจำนวนดาวเคราะห์กับอุณหภูมิยังผลและโชติมาตรของดาวหลัก

ดาว TRAPPIST-1 ซึ่งเป็นสีแสดด้านบนค่อนข้างโดดเด่นในนี้ทีเดียว
จากนั้นลองดูความสัมพันธ์ระหว่างจำนวนดาวเคราะห์กับมวลและขนาดของดาวหลักด้วย
สรุป
สุดท้ายนี้ลองสรุปค่าต่างๆหลายอย่างในตารางข้อมูลดู
* มวลดาวเคราะห์มีบางส่วนที่เป็นแค่ค่ามวลขั้นต่ำ Msin(i) ไม่ใช่มวลจริง ดังที่ได้อธิบายไปแล้ว
ทั้งหมดนี้ก็เป็นการสรุปข้อมูลของดาวเคราะห์นอกระบบสุริยะที่ค้นพบมาทั้งหมด ที่จริงยังมีเรื่องน่าสนใจน่าพูดถึงอีกมาก แต่อาจทำให้ยาวเกินไปจึงขอเขียนเพียงเท่านี้
ในนี้ใช้คำสั่งต่างๆใน pandas มากมาย แต่ไม่ได้อธิบายรายละเอียดใดๆเลย แต่ก็น่าจะใช้เป็นตัวอย่างของการนำมาประยุกต์ได้
ต้องขอบคุณทั้ง pandas ที่สามารถทำให้วิเคราะห์ข้อมูลได้ง่ายๆแบบนี้ และ astroquery ที่ทำให้สามารถดึงข้อมูลดาราศาสตร์มาใช้ได้ง่ายดาย
ดาวเคราะห์นอกระบบสุริยะมีการค้นพบใหม่มากขึ้นเรื่อยๆสม่ำเสมอ แม้เวลาที่อ่านบทความนี้ก็ยังมีดาวดวงใหม่รอการค้นพบอีกมากมาย น่าติดตามกันต่อไป
อ้างอิง
เนื่องในโอกาสนี้เลยอยากจะสรุปเกี่ยวกับดาวเคราะห์นอกระบบสุริยะ (太陽系外惑星) ทั้งหมดที่มีการค้นพบในช่วงตลอดเวลาที่ผ่านมานี้สักหน่อย
ดาวเคราะห์นอกระบบสุริยะก็คือดาวเคราะห์นอกเหนือจากดาวเคราะห์ ๘ ดวงที่พวกเรารู้จักกันดี คือ ดาวพุธ ดาวศุกร์ โลก ดาวอังคาร ดาวพฤหัส ดาวเสาร์ ดาวยูเรนัส ดาวเนปจูน (เมื่อก่อนรวมดาวพลูโตด้วยเป็น ๙ ดวง)
มนุษย์มองดูดาวมาตั้งแต่อดีต ตั้งแต่รู้ว่าดวงอาทิตย์แท้จริงก็เป็นแค่ดาวฤกษ์ดวงหนึ่งเหมือนกับดาวนับล้านที่อยู่บนฟ้าก็ย่อมมีความคิดว่ารอบๆดาวเหล่านั้นเองก็อาจมีดาวเคราะห์โคจรอยู่ด้วยเช่นกัน
ความพยายามในการค้นหาดาวเคราะห์นอกระบบสุริยะนั้นมีมาตั้งแต่อดีต แต่เพิ่งจะยืนยันการค้นพบแน่นอนได้ในปี 1995
จนถึงตอนนี้ซึ่งเพิ่งสิ้นสุดยุคเฮย์เซย์ไป จำนวนดาวเคราะห์นอกระบบสุริยะที่ค้นพบแล้วมีทั้งหมดประมาณ ๔๐๐๐ ดวง
สำหรับในบทความนี้จะเขียนโปรแกรมภาษาไพธอน โดยใช้มอดูล pandas และ matplotlib เป็นหลัก เพื่อวิเคราะห์ข้อมูลของดาวเคราะห์เหล่านั้น
บทความนี้เริ่มแรกเขียนเป็นภาษาญี่ปุ่นลงในบล็อก qiita https://qiita.com/phyblas/items/ec29c49302c7b0a60905
เนื้อหาที่ลงตรงนี้เป็นการเรียบเรียงใหม่เป็นภาษาไทย
สารบัญ
การดึงข้อมูลมาใช้
วิธีการค้นหา
อุปกรณ์สังเกตการณ์
ขนาดของดาวเคราะห์
ขนาดของดาวหลัก
ขนาดของดาวเคราะห์เทียบกับดาวหลัก
คาบการโคจรของดาวเคราะห์
มุมเอียงวงโคจรของดาวเคราะห์
มวลของดาวเคราะห์
มวลของดาวหลัก
ความหนาแน่นของดาวเคราะห์
ตำแหน่งบนทรงกลมท้องฟ้า
ระยะห่างจากโลก
ความสว่างของดาวหลัก
อุณหภูมิยังผลของดาวหลัก
จำนวนดาวเคราะห์ในระบบ
สรุป
วิธีการค้นหา
อุปกรณ์สังเกตการณ์
ขนาดของดาวเคราะห์
ขนาดของดาวหลัก
ขนาดของดาวเคราะห์เทียบกับดาวหลัก
คาบการโคจรของดาวเคราะห์
มุมเอียงวงโคจรของดาวเคราะห์
มวลของดาวเคราะห์
มวลของดาวหลัก
ความหนาแน่นของดาวเคราะห์
ตำแหน่งบนทรงกลมท้องฟ้า
ระยะห่างจากโลก
ความสว่างของดาวหลัก
อุณหภูมิยังผลของดาวหลัก
จำนวนดาวเคราะห์ในระบบ
สรุป
การดึงข้อมูลมาใช้
ข้อมูลดาวเคราะห์นั้นสามารถดูได้จากเว็บไซต์ต่างๆ จะโหลดมาก็ได้ แต่ถ้าใช้มอดูลในไพธอนมีวิธีที่จะดึงข้อมูลดาราศาสตร์มาง่ายๆโดยไม่ต้องไปโหลดจากเว็บเอง
มอดูลนั้นชื่อว่า astroquery เป็นมอดูลลูกของมอดูล astropy ที่ใช้กันกว้างขวางในวงการดาราศาสตร์
สามารถลงได้ง่ายด้วย pip หรือ conda
pip install --pre astroquery
conda install -c astropy astroqueryที่จะใช้ตรงนี้คือฐานข้อมูล NasaExoplanetArchive เป็นฐานข้อมูลที่เก็บข้อมูลของดาวเคราะห์นอกระบบสุริยะเอาไว้
รายละเอียดอ่านได้ในเว็บ https://exoplanetarchive.ipac.caltech.edu/index.html
จากเว็บนี้จะค้นข้อมูลของดาวเคราะห์หรือโหลดมาก็ได้ แต่ถ้าใช้ astroquery ก็จะโหลดข้อมูลเข้ามาในโปรแกรมไพธอนแล้วใช้วิเคราะห์ได้ทันที ไม่ต้องไปโหลดจากเว็บมาเองก่อน
from astroquery.nasa_exoplanet_archive import NasaExoplanetArchive
# มอดูลเหล่านี้จากนี้ไปจะใช้ด้วย ขอนำเข้ามาเตรียมไว้ก่อนเลย
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
table = NasaExoplanetArchive.get_confirmed_planets_table()
print(table)pl_hostname pl_letter pl_name ... NAME_LOWERCASE sky_coord
... deg,deg
------------ --------- -------------- ... -------------- ---------------------
Kepler-92 b Kepler-92 b ... kepler-92b 289.086058,41.562941
Kepler-92 c Kepler-92 c ... kepler-92c 289.086058,41.562941
Kepler-93 b Kepler-93 b ... kepler-93b 291.418281,38.672354
Kepler-93 c Kepler-93 c ... kepler-93c 291.418281,38.672354
Kepler-94 b Kepler-94 b ... kepler-94b 281.194747,47.497148
Kepler-94 c Kepler-94 c ... kepler-94c 281.194747,47.497148
... ... ... ... ... ...
K2-256 b K2-256 b ... k2-256b 186.227158,-2.065931
K2-257 b K2-257 b ... k2-257b 188.278488,-1.953159
K2-258 b K2-258 b ... k2-258b 187.631332,-1.16092
K2-259 b K2-259 b ... k2-259b 186.802689,1.566849
IC 4651 9122 b IC 4651 9122 b ... ic46519122b 261.208618,-49.948917
HD 26965 b HD 26965 b ... hd26965b 63.818001,-7.652871
Wolf 503 b Wolf 503 b ... wolf503b 206.847687,-6.136875
Length = 3946 rowsเมื่อใช้คำสั่ง get_confirmed_planets_table แล้วก็จะได้ข้อมูลเป็นตารางมาอย่างที่เห็น
จากตารางจะพบว่ามีดาวเคราะห์นอกระบบที่ยืนยันแล้วทั้งหมด ๓๙๔๖ ดวง
ข้อมูลนี้เป็นส่วนที่ลงในเว็บแล้วเท่านั้น อาจยังมีส่วนที่ไม่ได้ลง และข้อมูลจากเว็บต่างๆก็อาจไม่เหมือนกัน เช่นอีกเว็บคือ http://exoplanet.eu มักจะมีข้อมูลมากกว่า
ในที่นี้จะใช้ข้อมูล NasaExoplanetArchive ที่โหลดมาตอนขึ้นยุคเรย์วะพอดี คือเที่ยงคืนกว่าของวันที่ 1 พฤษภาคม ตามเวลาญี่ปุ่น
เมื่อใช้คำสั่งดึงข้อมูลนี้ไปแล้วข้อมูลก็จะถูกโหลดเข้ามา เวลาที่ใช้ครั้งต่อไปข้อมูลจะไม่มีการโหลดใหม่ แต่ไปใช้ข้อมูลที่เก็บไว้ในเครื่อง ทำให้ใช้งานได้เร็วขึ้น เพียงแต่ปัญหาคือข้อมูลพวกนี้มีการเพิ่มเติมเปลี่ยนแปลงอยู่สม่ำเสมอ ดังนั้นควรจะโหลดใหม่เรื่อยๆดีกว่า
เพื่อที่จะให้โหลดใหม่ทุกครั้ง ให้เติม cache=0 ลงไปด้วย
table = NasaExoplanetArchive.get_confirmed_planets_table(cache=0)ตารางข้อมูลที่ได้มานี้เป็นออบเจ็กต์ชนิด QTable ของ astropy ซึ่งถ้าไม่คุ้นเคยก็อาจใช้งานได้ไม่สะดวก ดังนั้นเพื่อให้ใช้งานคล่องจะเปลี่ยนเป็นข้อมูล DataFrame ของ pandas
df = pd.DataFrame({c: table[c] for c in table.columns})
df.set_index('pl_name',inplace=True)
print(df.columns.values)
print(df.shape)['pl_hostname' 'pl_letter' 'pl_discmethod' 'pl_controvflag' 'pl_pnum'
'pl_orbper' 'pl_orbpererr1' 'pl_orbpererr2' 'pl_orbperlim' 'pl_orbpern'
'pl_orbsmax' 'pl_orbsmaxerr1' 'pl_orbsmaxerr2' 'pl_orbsmaxlim'
'pl_orbsmaxn' 'pl_orbeccen' 'pl_orbeccenerr1' 'pl_orbeccenerr2'
'pl_orbeccenlim' 'pl_orbeccenn' 'pl_orbincl' 'pl_orbinclerr1'
'pl_orbinclerr2' 'pl_orbincllim' 'pl_orbincln' 'pl_bmassj'
'pl_bmassjerr1' 'pl_bmassjerr2' 'pl_bmassjlim' 'pl_bmassn' 'pl_bmassprov'
'pl_radj' 'pl_radjerr1' 'pl_radjerr2' 'pl_radjlim' 'pl_radn' 'pl_dens'
'pl_denserr1' 'pl_denserr2' 'pl_denslim' 'pl_densn' 'pl_ttvflag'
'pl_kepflag' 'pl_k2flag' 'ra_str' 'dec_str' 'ra' 'st_raerr' 'dec'
'st_decerr' 'st_posn' 'st_dist' 'st_disterr1' 'st_disterr2' 'st_distlim'
'st_distn' 'st_optmag' 'st_optmagerr' 'st_optmaglim' 'st_optband'
'gaia_gmag' 'gaia_gmagerr' 'gaia_gmaglim' 'st_teff' 'st_tefferr1'
'st_tefferr2' 'st_tefflim' 'st_teffn' 'st_mass' 'st_masserr1'
'st_masserr2' 'st_masslim' 'st_massn' 'st_rad' 'st_raderr1' 'st_raderr2'
'st_radlim' 'st_radn' 'pl_nnotes' 'rowupdate' 'pl_facility'
'NAME_LOWERCASE' 'sky_coord']
(3946, 83)ข้อมูลมี ๘๔ สดมภ์ (column) แต่ในที่นี้จะดึงสดมภ์ pl_name ซึ่งเก็บชื่อของดาวเคราะห์มาใช้เป็นดัชนี เหลือ ๘๓ สดมภ์
คำอธิบายของแต่ละสดมภ์มีเขียนไว้ใน https://exoplanetarchive.ipac.caltech.edu/docs/API_exoplanet_columns.html
จากนี้ไปจะใช้ข้อมูลจากตารางนี้เพื่อมาวิเคราะห์
วิธีการค้นหา
ก่อนอื่น หลายคนคงสงสัยว่าเราจะหาดาวเคราะห์ที่อยู่ไกลขนาดนั้นได้อย่างไร
วิธีการค้นหาดาวเคราะห์นอกระบบนั้นมีอยู่หลากหลาย ภายในข้อมูลนี้มีการบอกด้วยว่าดาวเคราะห์ดวงนั้นใช้วิธีการไหนค้นหา เขียนเอาไว้ในสดมภ์ pl_discmethod ลองดึงมาเขียนแผนภูมิแท่งสรุปกันดู
n_discmet = df.groupby('pl_discmethod').apply(len).sort_values(ascending=False)
lis_discmet = n_discmet.index
for i,(dm,n) in enumerate(n_discmet.iteritems()):
plt.text(n*0.9,i,'%d'%n,fontsize=12,ha='right',va='center',color='w')
n_met = len(n_discmet)
plt.barh(range(n_met),n_discmet,color='#665599')
plt.yticks(range(n_met),lis_discmet,fontsize=12)
plt.semilogx()
plt.tick_params(left=0)
plt.axes().invert_yaxis()
plt.tight_layout(0)
plt.show()
จะเห็นว่าภายในข้อมูลนี้มีอยู่ทั้งหมด ๑๐ วิธีการ ชื่อแต่ละวิธีหากเทียบแปลเป็นไทยก็จะเป็นดังนี้
Transit = การเคลื่อนผ่าน
Radial Velocity = ความเร็วแนวเล็ง
Microlensing = ไมโครเลนส์โน้มถ่วง
Imaging = การถ่ายภาพโดยตรง
Transit Timing Variation = ความแปรปรวนของเวลาเคลื่อนผ่าน
Eclipse Timing Variations = ความแปรปรวนของเวลาเกิดคราส
Pulsar Timing = การจับเวลาพัลซาร์
Orbital Brightness Modulation = การผันผวนของความสว่างวงโคจร
Pulsar Timing Variations = ความแปรปรวนของการจับเวลาพัลซาร์
Astrometry = มาตรดาราศาสตร์
รายละเอียดเกี่ยวกับแต่ละวิธีสามารถค้นได้ตามเว็บต่างๆ ในที่นี้จึงขอละไว้ ขอนำวิกิมาใช้อ้างอิง https://th.wikipedia.org/wiki/วิธีตรวจจับดาวเคราะห์นอกระบบ
อุปกรณ์สังเกตการณ์
มีกล้องโทรทรรศน์หรือหอดูดาวหลายแห่งที่ใช้ในการค้นพบดาวเคราะห์นอกระบบได้ ไม่ว่าจะเป็นกล้องโทรทรรศน์จากหอดูดาวบนพื้นโลก หรือกล้องโทรทรรศน์ที่ถูกส่งขึ้นไปในอวกาศ
ข้อมูลที่บอกว่าดาวเคราะห์ดวงนั้นๆถูกค้นพบด้วยเครื่องมือไหนก็ได้ใส่ไว้ในฐานข้อมูลนี้ด้วย อยู่ในสดมภ์ pl_facility ลองมาดูกัน
n_fac_dis = df.groupby('pl_facility').apply(len).sort_values(ascending=False)
print(n_fac_dis)pl_facility
Kepler 2342
K2 360
La Silla Observatory 232
W. M. Keck Observatory 171
Multiple Observatories 116
SuperWASP 110
HATNet 57
HATSouth 57
OGLE 50
Haute-Provence Observatory 45
Anglo-Australian Telescope 35
SuperWASP-South 32
Lick Observatory 32
CoRoT 31
McDonald Observatory 28
MOA 23
Okayama Astrophysical Observatory 23
Paranal Observatory 17
Roque de los Muchachos Observatory 17
Bohyunsan Optical Astronomical Observatory 16
Las Campanas Observatory 14
Transiting Exoplanet Survey Satellite (TESS) 11
KELT 10
Gemini Observatory 9
Subaru Telescope 8
Thueringer Landessternwarte Tautenburg 8
Qatar 7
KMTNet 7
Multiple Facilities 7
Hubble Space Telescope 6
Fred Lawrence Whipple Observatory 6
XO 6
Calar Alto Observatory 5
TrES 5
KELT-North 5
KELT-South 4
Spitzer Space Telescope 3
Arecibo Observatory 3
United Kingdom Infrared Telescope 2
SuperWASP-North 2
Palomar Observatory 2
Parkes Observatory 2
Large Binocular Telescope Observatory 2
Cerro Tololo Inter-American Observatory 2
Xinglong Station 2
MEarth Project 2
Apache Point Observatory 1
European Southern Observatory 1
Yunnan Astronomical Observatory 1
Infrared Survey Facility 1
Kitt Peak National Observatory 1
Leoncito Astronomical Complex 1
Mauna Kea Observatory 1
Oak Ridge Observatory 1
Teide Observatory 1
WASP-South 1
Acton Sky Portal Observatory 1
dtype: int64ดูแล้วก็จะเห็นได้ว่าที่ค้นพบมานี้เกินกว่าครึ่งเป็นผลงานของกล้องเคพเลอร์ (Kepler)
กล้องเคพเลอร์ หรือชื่อเต็มว่ากล้องโทรทรรศน์อวกาศเคพเลอร์ (Kepler space telescope) เป็นกล้องโทรทรรศน์ที่ถูกส่งขึ้นไปในอวกาศตั้งแต่ปี 2009 เพื่อค้นหาดาวเคราะห์ด้วยวิธีการเคลื่อนผ่าน และปลดประจำการในปี 2018
ตั้งแต่ปี 2009 ถึง 2013 กล้องเคพเลอร์ทำการสังเกตการณ์ด้วยสภาพที่สมบูรณ์เต็มที่ แต่หลังจากนั้นล้อปฏิกิริยา (reaction wheel) เกิดชำรุดขึ้นเป็นอันที่ ๒ ตั้งแต่ปี 2014 จึงเปลี่ยนชื่อเรียกเป็น K2 แล้วทำการสังเกตการณ์ต่อไปในสภาพที่ด้อยลงกว่าเดิม
ในฐานข้อมูลนี้ที่เขียนว่า Kepler หมายถึงกล้องเคพเลอร์ช่วงปี 2009 ถึง 2013 แต่ถ้าเป็นกล้องเคพเลอร์ในช่วงที่ใช้ชื่อว่า K2 ก็จะเขียนว่า K2 แยกกัน
K2 นั้นด้อยลงว่ากล้องเคพเลอร์ตอนช่วงแรก แต่ก็ยังค้นพบดาวเคราะห์ได้มากมายเช่นกัน
ดาวเทียมสำรวจดาวเคราะห์นอกระบบ Transiting Exoplanet Survey Satellite (TESS) เป็นผู้สืบทอดของกล้องเคพเลอร์ จะทำการสังเกตการณ์ค้นหาดาวเคราะห์ด้วยวิธีการเคลื่อนผ่านเช่นกัน
สำหรับหอดูดาวภาคพื้นดินที่สร้างผลงานมากที่สุดก็คือ หอดูดาวลาซียา (La Silla Observatory) ที่ทะเลทรายอาตากามา ประเทศชิลี
มีไม่น้อยที่ใช้กล้องโทรทรรศน์จากหลายแห่งร่วมกันในการค้นพบ
ส่วนของญี่ปุ่นก็มีหอดูดาวโอกายามะ (岡山天体物理観測所) ค้นหาดาวเคราะห์ด้วยวิธีความเร็วแนวเล็ง
print(df[df.pl_facility=='Okayama Astrophysical Observatory'].index.values)['HD 14067 b' '6 Lyn b' '14 And b' '18 Del b' '75 Cet b' '81 Cet b'
'HD 81688 b' 'eps Tau b' 'nu Oph b' 'nu Oph c' 'ome Ser b' 'omi CrB b'
'omi UMa b' 'xi Aql b' 'HD 104985 b' 'HD 120084 b' 'HD 2952 b'
'HD 5608 b' 'gam Lib b' 'gam Lib c' '24 Boo b' 'HD 47366 b' 'HD 47366 c']นอกจากนี้ยังมีกล้องโทรทรรศน์สึบารุ (すばる望遠鏡) อยู่ที่ฮาวายแต่ก็เป็นของญี่ปุ่น ใช้ทั้งวิธีความเร็วแนวเล็ง และวิธีการถ่ายภาพโดยตรง ในการค้นหาดาวเคราะห์
print(df[df.pl_facility=='Subaru Telescope'].pl_discmethod)pl_name
HD 17156 b Radial Velocity
HD 38801 b Radial Velocity
kap And b Imaging
DH Tau b Imaging
GJ 504 b Imaging
HD 145457 b Radial Velocity
HD 149026 b Radial Velocity
HD 180314 b Radial Velocity
Name: pl_discmethod, dtype: objectขนาดของดาวเคราะห์
ขนาดของดาวเคราะห์ถูกเขียนไว้ที่สดมภ์ pl_radj ส่วนขนาดของดาวฤกษ์ที่เป็นดาวหลักอยู่ที่สดมภ์ st_rad
เพียงแต่หน่วยที่ใช้จะต่างกัน ขนาดดาวเคราะห์ใช้หน่วยเป็นจำนวนเท่าของดาวพฤหัส ส่วนของดาวหลักใช้เป็นจำนวนเท่าของดวงอาทิตย์
เนื่องจากใช้หน่วยเป็นจำนวนเท่า ขนาดที่ว่านี้อาจหมายถึงรัศมีหรือเส้นผ่านศูนย์กลางก็ได้ มีความหมายไม่ต่างกัน
ยังมีดาวเคราะห์บางดวงที่ไม่ได้ถูกวัดขนาด ซึ่งส่วนที่ไม่มีข้อมูลนั้นจะถูกเขียนเป็น 0 ไป ดังนั้นก่อนที่จะวิเคราะห์ข้อมูลขนาดควรจะต้องตัดส่วนนั้นทิ้งก่อน
df1 = df[df.pl_radj>0]
print(df1.pl_radj.describe())count 3080.000000
mean 0.370629
std 0.422444
min 0.030000
25% 0.140000
50% 0.208000
75% 0.315000
max 6.900000
Name: pl_radj, dtype: float64จากข้อมูลจะเห็นได้ว่าจากดาวทั้ง ๓๙๔๖ ดวง มีอยู่แค่ ๓๐๘๐ ดวงที่รู้ขนาด ส่วนที่เหลือไม่มีข้อมูล
ดาวที่หาเจอด้วยวิธีการความเร็วแนวเล็งและไมโครเลนส์โน้มถ่วงนั้นปกติจะไม่สามารถรู้ขนาดของดาวเคราะห์ได้
สำหรับดาวที่ค้นพบด้วยวิธีความเร็วแนวเล็งนั้นอาจจะสังเกตการณ์ด้วยวิธีอื่นเพื่อหาขนาดได้ จึงมีบางส่วนที่รู้ขนาด แต่สำหรับดาวที่ค้นพบด้วยวิธีไมโครเลนส์โน้มถ่วงนั้นจะสังเกตการณ์ซ้ำด้วยวิธีอื่นได้ยาก จึงไม่มีดวงไหนที่รู้ขนาดเลย
ลองดูจำนวนดาวเคราะห์ที่ค้นพบด้วยวิธีต่างๆเฉพาะที่รู้รัศมี
print(df1.groupby('pl_discmethod').apply(len).sort_values(ascending=False))pl_discmethod
Transit 3042
Imaging 15
Radial Velocity 13
Transit Timing Variations 7
Orbital Brightness Modulation 3
dtype: int64ลองดูดาวที่เล็กและใหญ่ที่สุด
print(df1.loc[[df1.pl_radj.idxmin(),df1.pl_radj.idxmax()]].pl_radj)pl_name
Kepler-37 b 0.03
HD 100546 b 6.90
Name: pl_radj, dtype: float64ขนาดใหญ่สุดใหญ่ถึง ๖.๙ เท่าของดาวพฤหัส ดาวที่ใหญ่กว่าดาวพฤหัสมีอยู่ไม่น้อย แต่ก็มีขีดจำกัดอยู่ เพราะถ้าใหญ่เกินไปอาจถูกมองว่าเป็นดาวแคระน้ำตาล (褐色矮星) ได้
ดาวแคระน้ำตาลคือดาวฤกษ์ชนิดที่มีขนาดเล็กที่สุด มักสับสนกับดาวเคราะห์ขนาดใหญ่ได้ง่าย
โลกมีขนาดเป็น ๐.๐๘๙๒๑ เท่าของดาวพฤหัส ดาวที่เล็กที่สุดคือ Kepler-37 b มีขนาดเป็น ๐.๐๓ เท่าของดาวพฤหัส นั่นคือ ๐.๓๕๔ เท่าของโลก
ดาวเคราะห์ที่เล็กที่สุดในระบบสุริยะคือดาวพุธซึ่งมีขนาด ๐.๓๘๓ เท่าของโลก ดาวเคราะห์ที่เล็กกว่าดาวพุธเท่าที่พบมาจนถึงตอนนี้มีแค่ Kepler-37 b นี้เท่านั้น
ดาวเคราะห์ที่เล็กกว่าโลกที่ค้นพบแล้วก็มีอยู่ไม่น้อย ลองดูว่ามีกี่ดวงที่ใหญ่กว่าดาวพฤหัสและเล็กกว่าโลก
print((df1.pl_radj>1).sum()) # ดาวที่ใหญ่กว่าดาวพฤหัส
print((df1.pl_radj<0.08921).sum()) # ดาวที่เล็กกว่าโลก387
157ลองดูการแจกแจงขนาดดาวเคราะห์
plt.hist(np.log10(df1.pl_radj),100,ec='k')
plt.xlabel('ขนาดดาวเคราะห์ ($R_J$)',fontname='Tahoma')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()
ขนาดของดาวหลัก
ต่อไปดูขนาดของดาวฤกษ์ที่เป็นดาวหลักของดาวเคราะห์
st_rad = df[df.st_rad>0].drop_duplicates('pl_hostname').st_rad
print(st_rad.describe())count 2720.000000
mean 1.689048
std 4.083175
min 0.040000
25% 0.810000
50% 0.990000
75% 1.280000
max 71.230000
Name: st_rad, dtype: float64การแจกแจงขนาดดาวหลัก
plt.hist(np.log10(st_rad),100,ec='k')
plt.xlabel('ขนาดดาวหลัก ($R_S$)',fontname='Tahoma')
xtick = np.arange(-1,3.)
plt.xticks(xtick,10**xtick)
plt.show()
ขนาดของดาวเคราะห์เทียบกับดาวหลัก
ต่อไปมาเปรียบเทียบขนาดของดาวเคราะห์และดาวหลักดู แต่ก่อนอื่นต้องเปลี่ยนหน่วยให้เท่ากันก่อน
ขนาดของดาวพฤหัสเป็น ๐.๑๐๐๔๙ เท่าของดวงอาทิตย์
df1 = df[(df.pl_radj>0)&(df.st_rad>0)]
pl_rad = df1.pl_radj*0.10049
st_rad = df1.st_rad
rp_rs = pl_rad / st_rad
print(rp_rs.describe())count 3070.000000
mean 0.036103
std 0.041042
min 0.003816
25% 0.015219
50% 0.023031
75% 0.035952
max 1.042863
dtype: float64ดาวเคราะห์ที่อัตราส่วนขนาดต่อดาวหลักสูงสุดนั้นอัตราส่วนสูงกว่า ๑ นั่นหมายความว่าใหญ่ยิ่งกว่าดาวหลักเสียอีก ที่จริงดาวนั้นไม่ได้ใหญ่เป็นพิเศษ แค่ดาวหลักเป็นดาวแคระน้ำตาลซึ่งมีขนาดเล็กมากเท่านั้น
df2 = pd.DataFrame({'rp': pl_rad, 'rs': st_rad, 'rp_rs': rp_rs})
print(df2.loc[[rp_rs.idxmin(),rp_rs.idxmax()]])rp rs rp_rs
pl_name
Kepler-37 b 0.003015 0.79 0.003816
WISEP J121756.91+162640.2 A b 0.093858 0.09 1.042863จากนั้นมาดูการแจกแจงของขนาดดาวเคราะห์และดาวหลัก ในที่นี้จะใส่โลกกับดาวพฤหัสลงไปด้วยเพื่อเปรียบเทียบ
plt.axes(xlim=[pl_rad.min(),pl_rad.max()],ylim=[st_rad.min(),st_rad.max()],aspect=1)
x = np.array([0,pl_rad.max()])
for r in np.logspace(-3,0,4):
plt.plot(x,x/r,'k--')
plt.scatter(pl_rad,st_rad,c=rp_rs,norm=mpl.colors.LogNorm(),marker='.',cmap='jet')
plt.xlabel('ขนาดดาวเคราะห์ ($R_S$)',fontname='Tahoma')
plt.ylabel('ขนาดดาวฤกษ์ ($R_S$)',fontname='Tahoma')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='อัตราส่วนขนาดดาว',family='Tahoma')
plt.scatter([0.0091577],[1],70,c='r',marker='x')
plt.scatter([0.10049],[1],140,c='m',marker='+')
plt.loglog()
plt.show()
× ทางซ้ายคือโลก ส่วน + ทางขวาคือดาวพฤหัส
ดูแล้วจะเห็นว่าน่าสนใจตรงที่ขนาดของดาวเคราะห์หลักๆแบ่งออกเป็น ๒ กลุ่มก้อนใหญ่ คือกลุ่มที่ใกล้เคียงโลกและกลุ่มที่ใกล้เคียงดาวพฤหัส
คาบการโคจรของดาวเคราะห์
คาบการโคจรของดาวเคราะห์เขียนอยู่ที่สดมภ์ pl_orbper หน่วยเป็นวัน
pl_orbper = df[(df.pl_orbper>0)].pl_orbper
print(pl_orbper.describe())count 3.842000e+03
mean 2.357470e+03
std 1.181497e+05
min 9.070629e-02
25% 4.567262e+00
50% 1.198999e+01
75% 4.237136e+01
max 7.300000e+06
Name: pl_orbper, dtype: float64ดูการกระจาย
plt.hist(np.log10(pl_orbper),80,ec='k')
plt.xlabel('คาบการโคจร (วัน)',fontname='Tahoma')
xtick = np.arange(-1,7.)
plt.xticks(xtick,['$10^{%d}$'%x for x in xtick])
plt.show()
ยิ่งคาบการโคจรสั้นก็หมายความว่าดาวเคราะห์จะเคลื่อนผ่านดาวหลักบ่อยขึ้น ยิ่งอยู่ใกล้ผลของแรงโน้มถ่วงก็ยิ่งมาก ดังนั้นดาวเคราะห์ที่คาบวงโคจรสั้นจึงหาง่ายทั้งด้วยวิธีความเร็วแนวแล็งและวิธีการเคลื่อนผ่าน
ในระบบสุริยะดาวเคราะห์ที่อยู่ใกล้สุดคือดาวพุธซึ่งมีคาบการโคจร ๘๗.๙๖๙ วัน นั่นแสดงว่าดาวเคราะห์ส่วนใหญ่ที่ค้นพบมาแล้วนั้นมีขนาดวงโคจรอยู่ในระดับที่แคบกว่ามาตรฐานของระบบสุริยะ
นี่อาจเป็นผลจากความโน้มเอียงในการค้นหา แต่ก็ทำให้รู้ว่ามีระบบดาวเคราะห์ที่ต่างไปจากระบบสุริยะมากแบบนี้อยู่ไม่น้อย
ลองเทียบขนาดดาวเคราะห์และคาบวงโคจรของดาวเคราะห์ที่ค้นพบด้วยวิธีต่างๆดู
df1 = df[(df.pl_radj>0)&(df.pl_orbper>0)]
print(len(df1))
df2 = df1[df1.pl_discmethod=='Transit']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.',alpha=0.4)
df2 = df1[df1.pl_discmethod=='Radial Velocity']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
df2 = df1[df1.pl_discmethod=='Imaging']
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
df2 = df1[(df1.pl_discmethod!='Transit')&(df1.pl_discmethod!='Radial Velocity')&(df1.pl_discmethod!='Imaging')]
plt.scatter(df2.pl_radj,df2.pl_orbper,marker='.')
plt.xlabel('ขนาดดาวเคราะห์ ($R_J$)',fontname='Tahoma')
plt.ylabel('คาบการโคจร (วัน)',fontname='Tahoma')
plt.legend(['การเคลื่อนผ่าน','ความเร็วแนวเล็ง','ถ่ายภาพโดยตรง','อื่นๆ'],prop={'family':'Tahoma'})
plt.loglog()
plt.show()
จะเห็นว่าดาวเคราะห์ที่พบด้วยวิธีความเร็วแนวเล็งและวิธีการเคลื่อนผ่านจะมีคาบสั้น แต่ดาวที่พบจากการถ่ายภาพโดยตรงจะมีขนาดใหญ่และคาบยาว
มุมเอียงวงโคจรของดาวเคราะห์
มุมเอียงวงโคจรของดาวเคราะห์เมื่อมองจากโลกเขียนอยู่ในสดมภ์ pl_orbincl แต่ที่มีข้อมูลมีอยู่ไม่มาก
ถ้าวงโคจรตั้งฉากกับมุมมองจากโลกก็จะเจอด้วยวิธีการเคลื่อนผ่านได้ง่าย ดังนั้นดาวเคราะห์ส่วนใหญ่ที่ค้นพบจึงมีมุมเอียงวงโคจรอยู่ที่ประมาณ ๘๐-๙๐ ซะมาก
pl_orbincl = df[(df.pl_orbincl>0)].pl_orbincl
print(pl_orbincl.describe())
plt.hist(pl_orbincl,50,ec='k')
plt.xlabel('มุมเอียงวงโคจร',fontname='Tahoma')
plt.show()count 771.000000
mean 86.100313
std 7.956823
min 7.700000
25% 86.010000
50% 88.010000
75% 89.210000
max 90.760000
Name: pl_orbincl, dtype: float64
มวลของดาวเคราะห์
มวลของดาวเคราะห์เขียนอยู่ที่สดมภ์ pl_bmassj หน่วยเป็นจำนวนเท่าของดาวพฤหัส
แต่ว่าข้อมูลส่วนหนึ่งในนี้ไม่ใช่มวลที่แท้จริง แต่เป็นแค่มวลขั้นต่ำ ซึ่งหมายถึง Msin(i)
โดยที่ i คือมุมเอียงวงโคจรเทียบกับโลก ส่วน M คือมวลจริงๆ
ที่เป็นแบบนี้เพราะว่าดาวเคราะห์ที่ค้นพบโดยวิธีความเร็วเชิงมุมจะวัดมวลโดยดูจากขนาดของสเปกตรัมที่เปลี่ยนแปลงจากปรากฏการณ์ดอพเลอร์ที่เกิดขึ้น ซึ่งความเปลี่ยนแปลงขึ้นอยู่กับมวล แต่ก็ขึ้นอยู่กับมุมเอียงที่ทำกับโลกด้วย
ดังนั้นค่าที่วัดได้จึงอยู่ในรูปของ Msin(i) คือถ้ามุมเอียงมากหมายความว่ามวลจริงๆจะมากกว่าค่านั้นมาก
หากดูที่สดมภ์ pl_bmassprov อันที่มวลแสดงเป็นค่ามวลขั้นต่ำจะเขียนว่า Msini
ดาวเคราะห์ที่ค้นพบด้วยวิธีความเร็วแนวเล็งหากไม่รู้มุมเอียงวงโคจรก็จะไม่รู้มวลที่แท้จริง รู้ได้แค่มวลขั้นต่ำ แต่ถ้ารู้มุมเอียงแล้วในสดมภ์ pl_bmassprov จะเขียนว่า Msin(i)/sin(i) แล้วค่ามวลก็จะถูกเขียนเป็นมวลจริงไว้แล้ว
หากมวลถูกวัดด้วยวิธีอื่น ใน pl_bmassprov จะเขียนว่า Mass เฉยๆ
df1 = df[(df.pl_bmassj>0)]
print(df1.pl_bmassj.describe())
print(df.groupby('pl_bmassprov').apply(len))count 1530.000000
mean 2.535104
std 4.431595
min 0.000060
25% 0.110840
50% 0.915500
75% 2.580000
max 55.590000
Name: pl_bmassj, dtype: float64
pl_bmassprov
Mass 824
Msin(i)/sin(i) 5
Msini 701
dtype: int64ลองมาดูการกระจายของมวลดาวเคราะห์เฉพาะที่รู้มวลแน่นอนแล้ว
df1 = df[(df.pl_bmassj>0)&(df.pl_bmassprov!='Msini')]
print(df1.pl_bmassj.describe())
plt.hist(np.log10(df1.pl_bmassj),50,ec='k')
plt.xlabel('มวลดาวเคราะห์ ($M_J$)',fontname='Tahoma')
xtick = np.arange(-4,2.)
plt.xticks(xtick,10**xtick)
plt.show()count 829.000000
mean 2.072610
std 4.088909
min 0.000060
25% 0.069220
50% 0.650000
75% 1.855000
max 30.000000
Name: pl_bmassj, dtype: float64
มวลของดาวหลัก
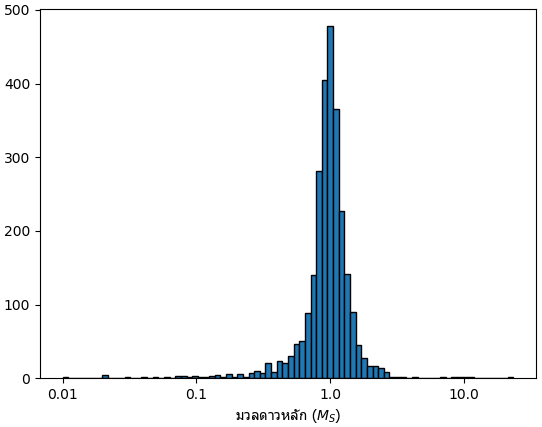
มวลของดาวหลักเขียนอยู่ที่สดมภ์ st_mass หน่วยเป็นจำนวนเท่าของมวลดวงอาทิตย์
st_mass = df[df.st_mass>0].drop_duplicates('pl_hostname').st_mass
print(st_mass.describe())
plt.hist(np.log10(st_mass),80,ec='k')
plt.xlabel('มวลดาวหลัก ($M_S$)',fontname='Tahoma')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()count 2633.000000
mean 1.027626
std 0.678201
min 0.010000
25% 0.830000
50% 0.980000
75% 1.140000
max 23.560000
Name: st_mass, dtype: float64
ดาวหลักที่มวลใกล้เคียงกับดวงอาทิตย์จะมีค่อนข้างเยอะ
ความหนาแน่นของดาวเคราะห์
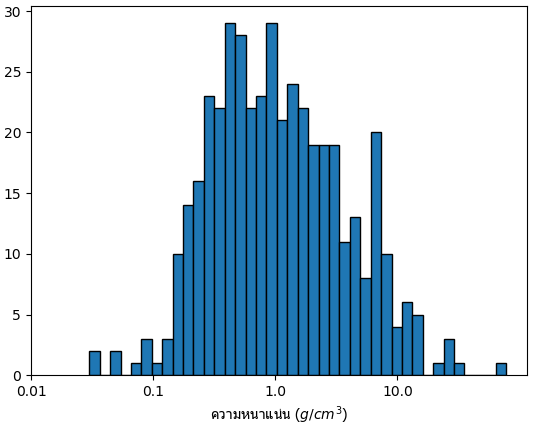
ค่าความหนานแน่นของดาวเคราะห์อยู่ที่สดมภ์ pl_dens หน่วยคือกรัมต่อลูกบาศก์เมตร แต่ที่มีข้อมูลมีอยู่น้อย และความไม่แน่นอนก็สูงด้วย
ความคลาดเคลื่อนของความหนาแน่นดูได้ที่สดมภ์ pl_denserr1 และ pl_denserr2
df1 = df[df.pl_dens>0]
print(df1.pl_dens.describe())
print(df1.loc[[df1.pl_dens.idxmin(),df1.pl_dens.idxmax()]][['pl_dens','pl_denserr1','pl_denserr2']])
plt.hist(np.log10(df1.pl_dens),40,ec='k')
plt.xlabel('ความหนาแน่น ($g/cm^3$)',fontname='Tahoma')
xtick = np.arange(-2,2.)
plt.xticks(xtick,10**xtick)
plt.show()count 435.000000
mean 2.509603
std 5.200267
min 0.030000
25% 0.410000
50% 0.964000
75% 2.500000
max 77.700000
Name: pl_dens, dtype: float64
pl_dens pl_denserr1 pl_denserr2
pl_name
Kepler-51 b 0.03 0.02 -0.01
Kepler-131 c 77.70 55.00 -55.00
ดาวที่มีความหนาแน่นมากที่สุดหนาแน่นถึง ๗๗.๗ g/cm3 แต่ก็มี ±๕๕ จึงมีความไม่แน่นอนมาก
ตำแหน่งบนทรงกลมท้องฟ้า
ค่าไรต์แอสเซนชัน (right ascention) และเดคลิเนชัน (declination) ซึ่งบอกตำแหน่งของดาวบนพิกัดทรงกลมท้องฟ้านั้นอยู่ในสดมภ์ ra และ dec หน่วยเป็นองศา
หากมองดูบนท้องฟ้าจะเห็นว่าตรงไหนก็เห็นดาวได้หมด การค้นหาดาวเคราะห์ก็ทำกับดาวทั่วท้องฟ้า แต่ว่าก็มีความโน้มเอียงในการค้นหาอยู่ ขึ้นอยู่กับวิธีการ
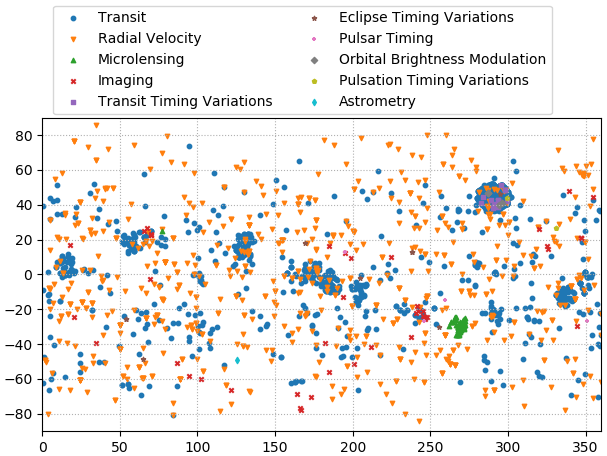
ลองดูการกระจายของตำแหน่งโดยแยกแต่ละวิธี
marker = ['o','v','^','x','s','*','+','D','p','d']
plt.axes(xlim=[0,360],ylim=[-90,90])
for d,m in zip(lis_discmet,marker):
plt.scatter(df.ra[df.pl_discmethod==d],df.dec[df.pl_discmethod==d],s=10,marker=m)
plt.legend(lis_discmet,loc=(0.02,1.01),ncol=2)
plt.grid(ls=':')
plt.tight_layout()
plt.show()
ดาวที่ค้นหาด้วยวิธีความเร็วแนวเล็งนั้นค่อนข้างกระจายสม่ำเสมอ แต่ที่หาด้วยวิธีการเคลื่อนผ่านกับวิธีไมโครเลนส์โน้มถ่วงจะรวมกันแน่นอยู่มากที่บางจุด
สาเหตุเป็นเพราะวิธีการไมโครเลนส์โน้มถ่วงนั้นจะได้ผลดีมากเฉพาะกับแถวใจกลางดาราจักรทางช้างเผือกซึ่งมีดาวอยู่หนาแน่นใช้เป็นฉากหลังได้
ส่วนวิธีการเคลื่อนผ่านนั้นที่จริงไม่ได้มีความแตกต่างมากถึงขนาดนั้น เพียงแต่ว่ากล้องเคพเลอร์นั้นได้ทำการค้นหาดาวเคราะห์อยู่แค่ที่บริเวณเล็กๆที่จำกัดไว้เท่านั้น จึงทำให้ดาวที่ค้นพบกระจุกอยู่ตรงนั้น
เคพเลอร์ในช่วงต้นจะส่งไปแค่บริเวณเล็กๆในกลุ่มดาวหงส์เท่านั้น ส่วนตอนที่เป็น K2 เปลี่ยนเป็นส่องไปรอบๆบริเวณใกล้ๆแนวสุริยวิถี
ในข้อมูลนี้มีสดมภ์ pl_kepflag และ pl_k2flag ซึ่งบอกว่าดาวเคราะห์ดวงนั้นอยู่ในเป้าหมายสังเกตการณ์ของเคพเลอร์หรือ K2 หรือไม่ (0=ไม่, 1=ใช่)
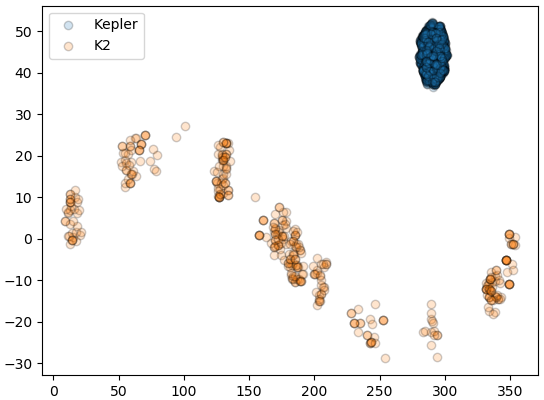
ดาวในกลุ่มนี้จะกระจายอยู่แค่ในบริเวณจำกัดเท่านั้น
df_k = df[df.pl_kepflag==1]
plt.scatter(df_k.ra,df_k.dec,edgecolor='k',alpha=0.2)
df_k2 = df[df.pl_k2flag==1]
plt.scatter(df_k2.ra,df_k2.dec,edgecolor='k',alpha=0.2)
plt.legend(['Kepler','K2'])
plt.show()
นั่นหมายความว่าดาวเกินกว่าครึ่งที่ค้นพบไปนั้นอยู่ในกลุ่มดาวหงส์ซึ่งเป็นเป้าหมายการสังเกตการณ์ของกล้องเคพเลอร์เท่านั้นเอง
หากลองเอาดาวที่เป็นเป้าหมายของเคพเลอร์และที่หาด้วยไมโครเลนส์โน้มถ่วงออกไปก็จะไม่มีบริเวณไหนที่กระจุกกันแน่นเป็นพิเศษอีก
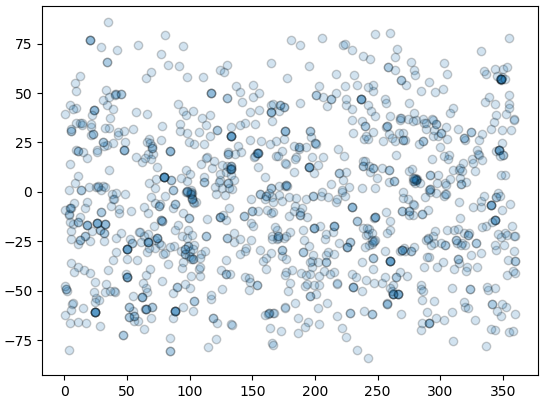
df1 = df[df.pl_kepflag+df.pl_k2flag+(df.pl_discmethod=='Microlensing')==0]
plt.scatter(df1.ra,df1.dec,edgecolor='k',alpha=0.2)
plt.show()
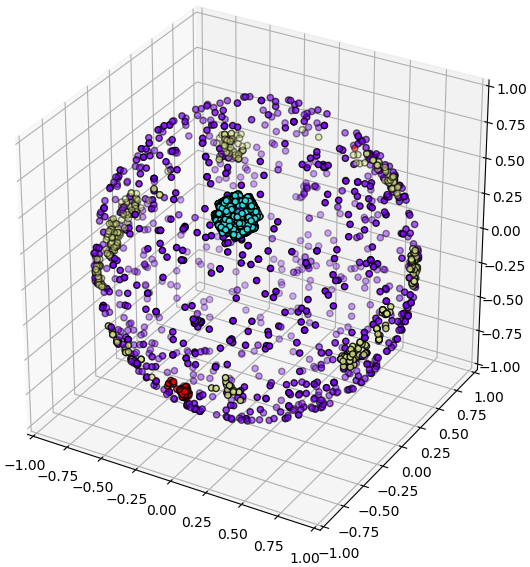
อาจลองแปลงจากไรต์แอสเซนชันและเดคลิเนชันไปเป็นทรงกลมท้องฟ้าในสามมิติดูการแจกแจงได้
x = np.cos(np.radians(df.dec))*np.cos(np.radians(df.ra))
y = np.cos(np.radians(df.dec))*np.sin(np.radians(df.ra))
z = np.sin(np.radians(df.dec))
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[-1,1],ylim=[-1,1],zlim=[-1,1])
c = (df.pl_discmethod=='Microlensing')*3+df.pl_kepflag+df.pl_k2flag*2
ax.scatter(x,y,z,c=c,edgecolor='k',cmap='rainbow')
plt.show()
ในที่นี้สีฟ้าและสีเทาคือดาวที่เป็นเป้าหมายของเคพเลอร์และ K2 ส่วนสีแดงคือที่ค้นด้วยวิธีไมโครเลนส์โน้มถ่วง
ระยะห่างจากโลก
ระยะห่างของระบบดาวเคราะห์นั้นจากโลกเขียนไว้ในสดมภ์ st_dist หน่วยเป็น pc
df1 = df[df.st_dist>0].drop_duplicates('pl_hostname')
print(df1.st_dist.describe())
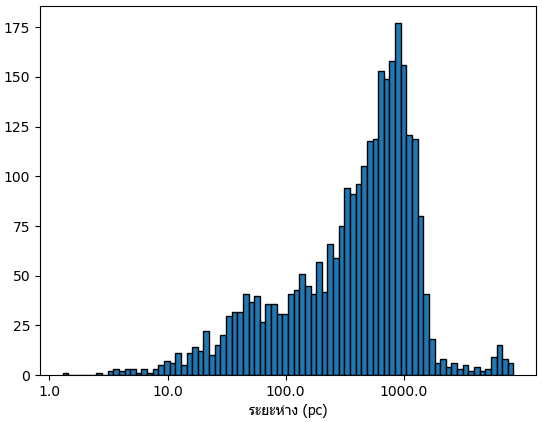
plt.hist(np.log10(df1.st_dist),80,ec='k')
plt.xlabel('ระยะห่าง (pc)',fontname='Tahoma')
xtick = np.arange(4.)
plt.xticks(xtick,10**xtick)
plt.show()count 2930.000000
mean 658.883689
std 875.723167
min 1.290000
25% 171.000000
50% 499.000000
75% 872.000000
max 8500.000000
Name: st_dist, dtype: float64
พื้นที่ของทรงกลมแปรตามกำลังสองของรัศมี ดังนั้นยิ่งไกลยิ่งมีดาวมาก แต่ถ้าไกลไปก็จะเห็นได้ยาก ดังนั้นจึงเจอมากสุดแถวๆ ๑๐๐๐ pc
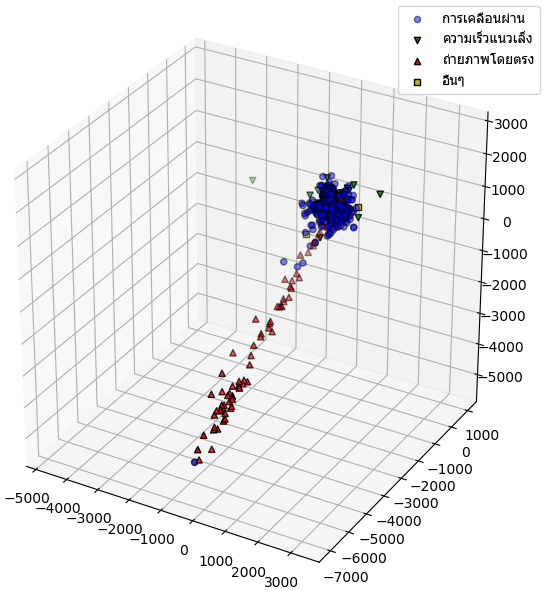
หากนำระยะห่างมาคำนวณเข้ากับไรต์แอสเซนชันและเดคลิเนชันก็จะแสดงการกระจายในปริภูมิสามมิติได้
x = np.cos(np.radians(df1.dec))*np.cos(np.radians(df1.ra))*df1.st_dist
y = np.cos(np.radians(df1.dec))*np.sin(np.radians(df1.ra))*df1.st_dist
z = np.sin(np.radians(df1.dec))*df1.st_dist
a,b,c = np.array([x.max()+x.min(),y.max()+y.min(),z.max()+z.min()])/2
m = max([x.max()-x.min(),y.max()-y.min(),z.max()-z.min()])/2
plt.figure(figsize=[6,6])
ax = plt.axes([0,0,1,1],projection='3d',xlim=[a-m,a+m],ylim=[b-m,b+m],zlim=[c-m,c+m])
c = df1.pl_discmethod=='Transit'
ax.scatter(x[c],y[c],z[c],c='b',edgecolor='k',cmap='rainbow',marker='o',alpha=0.5)
c = df1.pl_discmethod=='Radial Velocity'
ax.scatter(x[c],y[c],z[c],c='g',edgecolor='k',cmap='rainbow',marker='v',)
c = df1.pl_discmethod=='Microlensing'
ax.scatter(x[c],y[c],z[c],c='r',edgecolor='k',cmap='rainbow',marker='^')
c = (df1.pl_discmethod!='Transit')&\
(df1.pl_discmethod!='Radial Velocity')&\
(df1.pl_discmethod!='Microlensing')
ax.scatter(x[c],y[c],z[c],c='y',edgecolor='k',cmap='rainbow',marker='s')
plt.legend(['การเคลื่อนผ่าน','ความเร็วแนวเล็ง','ถ่ายภาพโดยตรง','อื่นๆ'],prop={'family':'Tahoma'})
plt.show()
ส่วนใหญ่จะอยู่ใน ๑๐๐๐ pc แต่ทางฝั่งหันไปทางใจกลางดาราจักรทางช้างเผือกนั้นมีดาวที่ค้นพบด้วยวิธีไมโครเลนส์โน้มถ่วงกระจัดกระจายอยู่มาก
ความสว่างของดาวหลัก
โชติมาตร (magnitude) หรือ อันดับความสว่าง เป็นค่าที่บอกถึงความสว่างของดาว ค่านี้ยิ่งน้อยยิ่งหมายถึงสว่างมาก
โชติมาตรของดาวหลักเขียนไว้ในสดมภ์ st_optmag
df1 = df[df.st_optmag>0].drop_duplicates('pl_hostname')
print(df1.st_optmag.describe())
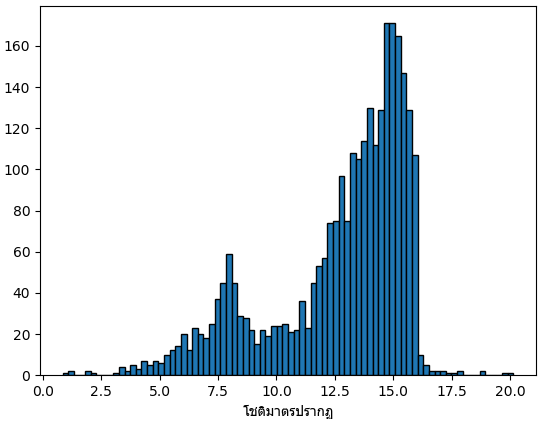
plt.hist(df1.st_optmag,80,ec='k')
plt.xlabel('โชติมาตรปรากฏ',fontname='Tahoma')
plt.show()count 2789.000000
mean 12.694392
std 2.965030
min 0.850000
25% 11.472000
50% 13.659000
75% 14.935000
max 20.150000
Name: st_optmag, dtype: float64
ดาวที่โชติมาตรต่ำส่วนใหญ่เป็นดาวที่เป็นที่รู้จักดี
st_optmag = df[df.st_optmag!=0].drop_duplicates('pl_hostname').set_index('pl_hostname').sort_values('st_optmag').st_optmag
print(st_optmag[st_optmag<3])pl_hostname
alf Tau 0.85
HD 62509 1.14
Fomalhaut 1.16
gam 1 Leo 1.98
alf Ari 2.00
bet UMi 2.08
Name: st_optmag, dtype: float64ดาวทั้ง ๖ นี้คือ
- อัลเดบาราน (Aldebaran) = α กลุ่มดาววัว
- ปอลลุกซ์ (Pollux) = β กลุ่มดาวคนคู่
- ฟอมาลเฮาต์ (Fomalhaut) = α กลุ่มดาวปลาทางใต้
- γ กลุ่มดาวสิงโต
- α กลุ่มดาวแกะ
- β กลุ่มดาวหมีเล็ก
โชติมาตรนี้เป็นโชติมาตรปรากฏที่มองจากโลก ซึ่งยิ่งไกลก็จะยิ่งเห็นมืดลง
ลองดูความสัมพันธ์ระหว่างขนาดดาวกับระยะทางจากโลกและโชติมาตร
df1 = df[(df.st_dist>0)&(df.st_rad>0)&(df.st_optmag>0)].drop_duplicates('pl_hostname')
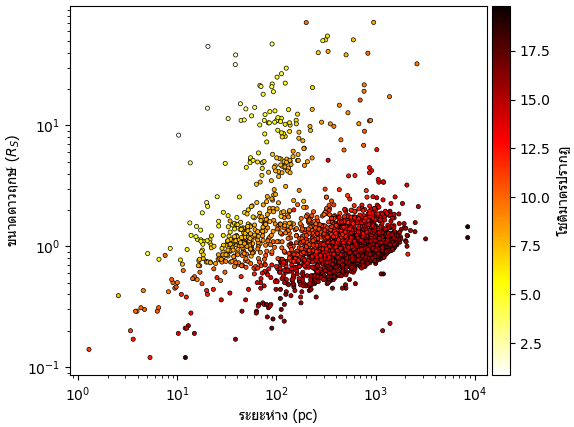
plt.scatter(df1.st_dist,df1.st_rad,c=df1.st_optmag,marker='.',cmap='hot_r',edgecolor='k',lw=0.5)
plt.xlabel('ระยะห่าง (pc)',fontname='Tahoma')
plt.ylabel('ขนาดดาวฤกษ์ ($R_S$)',fontname='Tahoma')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='โชติมาตรปรากฏ',family='Tahoma')
plt.loglog()
plt.show()
ถ้าจะแปลงเป็นโชติมาตรสัมบูรณ์ซึ่งแสดงความสว่างจริงของดาวก็คำนวณโดย
โชติมาตรสัมบูรณ์ = โชติมาตรปรากฏ + 5 - 5 log10(ระยะห่าง)
ลองคำนวณโชติมาตรสัมบูรณ์แล้วดูการแจกแจงดู
df1 = df[(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
print(st_mag.describe())
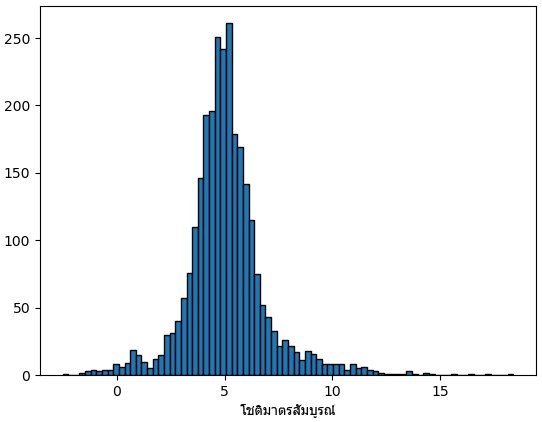
plt.hist(st_mag,80,ec='k')
plt.xlabel('โชติมาตรสัมบูรณ์',fontname='Tahoma')
plt.show()
อุณหภูมิยังผลของดาวหลัก
ค่าอุณหภูมิยังผลของดาวหลักเขียนไว้ที่สดมภ์ st_teff หน่วยเป็นเคลวิน
df1 = df[df.st_teff>0].drop_duplicates('pl_hostname').sort_values('st_teff',ascending=False)
print(df1.st_teff.describe())count 2807.000000
mean 5504.664400
std 1442.050143
min 575.000000
25% 5073.000000
50% 5617.000000
75% 5943.000000
max 57000.000000
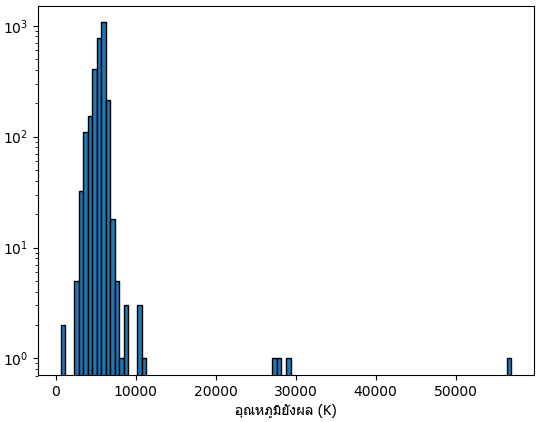
Name: st_teff, dtype: float64จะเห็นว่าดาวที่ร้อนที่สุดนั้นร้อนถึง ๕๗๐๐๐ เคลวิน แต่ว่าดาวนั้นค่อนข้างพิเศษ ที่จะร้อนขนาดนั้นมีไม่มาก ส่วนใหญ่จะอยู่ที่ ๕๐๐๐~๖๐๐๐ ใกล้เคียงดวงอาทิตย์
df1 = df[df.st_teff>0].drop_duplicates('pl_hostname').sort_values('st_teff',ascending=False)
print(df1.st_teff.describe())
print(df1.set_index('pl_hostname')[:6][['st_teff','st_optmag','st_rad','st_mass']].replace(0,'-'))
plt.hist(df1.st_teff,100,ec='k')
plt.xlabel('อุณหภูมิยังผล (K)',fontname='Tahoma')
plt.semilogy()
plt.show()
ลองดูชื่อดาวที่ร้อนเป็นพิเศษพวกนี้ดู
print(df1.set_index('pl_hostname')[:6][['st_teff','st_optmag','st_rad','st_mass']].replace(0,'-'))st_teff st_optmag st_rad st_mass
pl_hostname
NN Ser 57000.0 - - 0.54
V0391 Peg 29300.0 14.57 0.23 0.5
KOI-55 27730.0 14.87 0.2 0.5
KIC 10001893 27500.0 15.846 - -
kap And 10900.0 4.14 - 2.6
HIP 78530 10500.0 7.192 - 2.5ถ้านำอุณหภูมิยังผลและโชติมาตรสัมบูรณ์มาวาดกราฟก็จะได้แผนภาพแฮร์ทสชปรุง-รัสเซล
df1 = df[(df.st_teff>0)&(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
plt.scatter(df1.st_teff,st_mag,(20-st_mag)*5,c=df1.st_teff**0.25,marker='.',cmap='Spectral',edgecolor='k',lw=0.5)
plt.xlabel('อุณหภูมิยังผล (K)',fontname='Tahoma')
plt.ylabel('โชติมาตรสัมบูรณ์',fontname='Tahoma')
plt.xlim(df1.st_teff.max(),df1.st_teff.min())
plt.axes().invert_yaxis()
plt.show()
จำนวนดาวเคราะห์ในระบบ
จำนวนดาวเคราะห์ทั้งหมดที่ถูกค้นพบแล้วในแต่ละระบบถูกเขียนไว้ที่สดมภ์ pl_pnum
ลองมาดูกันว่าแต่ละระบบมีการค้นพบดาวกันมากแค่ไหนแล้ว
n_pl = np.bincount(df.drop_duplicates('pl_hostname').pl_pnum)[1:]
plt.bar(range(1,len(n_pl)+1),n_pl,color='#669955',ec='k')
for i,n in enumerate(n_pl,1):
plt.text(i,n,'%d'%n,ha='center',va='bottom')
plt.semilogy()
plt.tick_params(bottom=0)
plt.show()
ดูแล้วที่พบมากสุดคือ ๘ ดวง เท่ากับระบบสุริยะเลย
ลองดูชื่อของระบบที่มี ๗ และ ๘ ดวงนี้ดู
print(df[df.pl_pnum>=7][['pl_facility','pl_radj','pl_orbper']].sort_index())pl_facility pl_radj pl_orbper
pl_name
KOI-351 b Kepler 0.117 7.008151
KOI-351 c Kepler 0.106 8.719375
KOI-351 d Kepler 0.256 59.736670
KOI-351 e Kepler 0.237 91.939130
KOI-351 f Kepler 0.257 124.914400
KOI-351 g Kepler 0.723 210.606970
KOI-351 h Kepler 1.008 331.600590
KOI-351 i Kepler 0.118 14.449120
TRAPPIST-1 b La Silla Observatory 0.097 1.510871
TRAPPIST-1 c La Silla Observatory 0.094 2.421823
TRAPPIST-1 d La Silla Observatory 0.069 4.049610
TRAPPIST-1 e Multiple Observatories 0.082 6.099615
TRAPPIST-1 f Multiple Observatories 0.093 9.206690
TRAPPIST-1 g Multiple Observatories 0.101 12.352940
TRAPPIST-1 h Multiple Observatories 0.067 18.767000ระบบ ๘ ดวงนี้ชื่อ KOI-351 หรืออีกชื่อคือ Kepler-90 ซึ่งที่จริงแล้วเคยเขียนแนะนำไปในบทความก่อนหน้านี้ ว่าถูกค้นพบโดยปัญญาประดิษฐ์
อ่านได้ที่ https://phyblas.hinaboshi.com/20171216
ส่วนระบบที่มี ๗ ดวงคือ TRAPPIST-1 ซึ่งค้นพบโดยกล้องโทรทรรศน์ TRAPPIST ที่หอดูดาวลาซียา
น่าลองมาดูว่าดาวแบบไหนที่เจอดาวเคราะห์ได้มาก ลองดูสมบัติต่างๆของดาวที่มีดาวเคราะห์ถึง ๕ ดวงขึ้นไปกัน
df1 = df[df.pl_pnum>=5].drop_duplicates('pl_hostname').sort_values('pl_pnum',ascending=False)
df1['st_mag'] = df1.st_optmag+5-5*np.log10(df1.st_dist)
col = ['pl_pnum','st_teff','st_mag','st_rad','st_mass']
print(df1.set_index('pl_hostname')[col].replace(0,'-'))pl_pnum st_teff st_mag st_rad st_mass
pl_hostname
KOI-351 8 6080.0 4.343527 1.2 1.2
TRAPPIST-1 7 2559.0 18.386073 0.12 0.08
HD 34445 6 5879.0 4.007141 1.38 1.14
Kepler-20 6 5495.0 5.198010 0.96 0.95
HD 219134 6 4699.0 6.488794 0.78 0.81
Kepler-11 6 5663.0 5.262698 1.06 0.96
HD 10180 6 5911.0 4.364564 1.11 1.06
Kepler-80 6 4540.0 7.040659 0.68 0.73
Kepler-102 5 4909.0 6.285037 0.76 0.81
Kepler-84 5 6031.0 4.625214 1.17 -
Kepler-238 5 5751.0 4.401983 1.43 -
Kepler-444 5 5046.0 6.116659 0.75 0.76
Kepler-296 5 3740.0 9.150458 0.48 0.5
Kepler-292 5 5299.0 5.847986 0.83 -
HIP 41378 5 6199.0 3.791010 1.4 1.15
Kepler-122 5 6050.0 4.367544 1.22 -
Kepler-55 5 4503.0 7.019258 0.62 -
Kepler-62 5 4925.0 5.895761 0.64 0.69
GJ 667 C 5 3350.0 11.057455 - 0.33
Kepler-186 5 3755.0 8.447358 0.52 0.54
Kepler-33 5 5904.0 3.755524 1.82 1.29
Kepler-32 5 3900.0 9.044787 0.53 0.58
Kepler-169 5 4997.0 6.006551 0.76 -
55 Cnc 5 5196.0 5.459871 0.94 0.91
Kepler-154 5 5690.0 4.874169 1 -
Kepler-150 5 5560.0 5.149601 0.94 -
HD 40307 5 4956.0 6.610329 - 0.77
K2-138 5 5378.0 5.897745 0.86 0.93KOI-351 (Kepler-90) นั้นเป็นดาวที่ค่อนข้างใกล้เคียงกับดวงอาทิตย์ แต่ TRAPPIST-1 นั้นค่อนข้างมืดและเล็กมาก
ลองดูความสัมพันธ์ระหว่างจำนวนดาวเคราะห์กับอุณหภูมิยังผลและโชติมาตรของดาวหลัก
df1 = df[(df.st_teff>0)&(df.st_optmag>0)&(df.st_dist>0)].drop_duplicates('pl_hostname').sort_values('pl_pnum')
st_mag = df1.st_optmag+5-5*np.log10(df1.st_dist)
plt.scatter(df1.st_teff,st_mag,df1.pl_pnum*15,c=df1.pl_pnum,marker='.',cmap='jet',edgecolor='k',lw=0.5)
plt.xlabel('อุณหภูมิยังผล (K)',fontname='Tahoma')
plt.ylabel('โชติมาตร',fontname='Tahoma')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='จำนวนดาวเคราะห์',family='Tahoma')
plt.show()
ดาว TRAPPIST-1 ซึ่งเป็นสีแสดด้านบนค่อนข้างโดดเด่นในนี้ทีเดียว
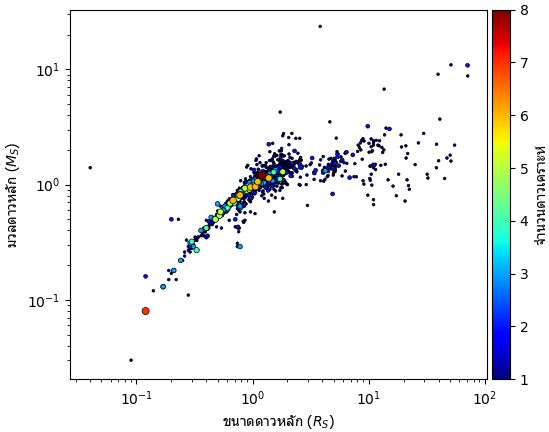
จากนั้นลองดูความสัมพันธ์ระหว่างจำนวนดาวเคราะห์กับมวลและขนาดของดาวหลักด้วย
df1 = df[(df.st_rad>0)&(df.st_mass>0)].drop_duplicates('pl_hostname').sort_values('pl_pnum')
plt.scatter(df1.st_rad,df1.st_mass,df1.pl_pnum*15,c=df1.pl_pnum,marker='.',cmap='jet',edgecolor='k',lw=0.5)
plt.xlabel('ขนาดดาวหลัก ($R_S$)',fontname='Tahoma')
plt.ylabel('มวลดาวหลัก ($M_S$)',fontname='Tahoma')
cb = plt.colorbar(pad=0.01)
cb.set_label(label='จำนวนดาวเคราะห์',family='Tahoma')
plt.loglog()
plt.show()
สรุป
สุดท้ายนี้ลองสรุปค่าต่างๆหลายอย่างในตารางข้อมูลดู
f = lambda x: pd.Series({"ต่ำสุด":x[x>0].min(),
"เฉลี่ย":x[x>0].mean(),
"มัธยฐาน":x[x>0].median(),
"สูงสุด":x.max()})
col = ['pl_radj','pl_bmassj','pl_dens','pl_orbincl','pl_orbper','st_dist']
pl = df[col].apply(f).transpose()
pl.index = ['รัศมีดาวเคราะห์','มวลดาวเคราะห์*','ความหนาแน่นดาวเคราะห์','มุมเอียงวงโคจร','คาบวงโคจร','ระยะห่างดาวเคราะห์']
pl['หน่วย'] = ['R_J','M_J','g/cm^3','องศา','วัน','pc']
col = ['st_rad','st_mass','st_optmag','st_teff','st_dist']
st = df.drop_duplicates('pl_hostname')[col].apply(f).transpose()
st.index = ['รัศมีดาวหลัก','มวลดาวหลัก','โชติมาตรดาวหลัก','อุณหภูมิยังผลดาวหลัก','ระยะห่างดาวหลัก']
st['หน่วย'] = ['R_S','M_S','mag','K','pc']
print(pd.concat([pl,st])) ต่ำสุด เฉลี่ย มัธยฐาน สูงสุด หน่วย
รัศมีดาวเคราะห์ 0.030000 0.370629 0.208000 6.90 R_J
มวลดาวเคราะห์* 0.000060 2.535104 0.915000 55.59 M_J
ความหนาแน่นดาวเคราะห์ 0.030000 2.509603 0.964000 77.70 g/cm^3
มุมเอียงวงโคจร 7.700000 86.100313 88.010000 90.76 องศา
คาบวงโคจร 0.090706 2357.470431 11.989985 7300000.00 วัน
ระยะห่างดาวเคราะห์ 1.290000 627.859352 492.000000 8500.00 pc
รัศมีดาวหลัก 0.040000 1.689048 0.990000 71.23 R_S
มวลดาวหลัก 0.010000 1.027626 0.980000 23.56 M_S
โชติมาตรดาวหลัก 0.850000 12.694392 13.659000 20.15 mag
อุณหภูมิยังผลดาวหลัก 575.000000 5504.664400 5617.000000 57000.00 K
ระยะห่างดาวหลัก 1.290000 658.883689 499.000000 8500.00 pc* มวลดาวเคราะห์มีบางส่วนที่เป็นแค่ค่ามวลขั้นต่ำ Msin(i) ไม่ใช่มวลจริง ดังที่ได้อธิบายไปแล้ว
ทั้งหมดนี้ก็เป็นการสรุปข้อมูลของดาวเคราะห์นอกระบบสุริยะที่ค้นพบมาทั้งหมด ที่จริงยังมีเรื่องน่าสนใจน่าพูดถึงอีกมาก แต่อาจทำให้ยาวเกินไปจึงขอเขียนเพียงเท่านี้
ในนี้ใช้คำสั่งต่างๆใน pandas มากมาย แต่ไม่ได้อธิบายรายละเอียดใดๆเลย แต่ก็น่าจะใช้เป็นตัวอย่างของการนำมาประยุกต์ได้
ต้องขอบคุณทั้ง pandas ที่สามารถทำให้วิเคราะห์ข้อมูลได้ง่ายๆแบบนี้ และ astroquery ที่ทำให้สามารถดึงข้อมูลดาราศาสตร์มาใช้ได้ง่ายดาย
ดาวเคราะห์นอกระบบสุริยะมีการค้นพบใหม่มากขึ้นเรื่อยๆสม่ำเสมอ แม้เวลาที่อ่านบทความนี้ก็ยังมีดาวดวงใหม่รอการค้นพบอีกมากมาย น่าติดตามกันต่อไป
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- ดาราศาสตร์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> pandas
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib