ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๘: การแจกแจงไคกำลังสอง
เขียนเมื่อ 2020/09/10 22:01
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๑๗
ในบทนี้จะเป็นเรื่องของการแจกแจงไคกำลังสอง (χ²分布, chi-square distribution) ซึ่งเป็นการแจกแจงความน่าจะเป็นแบบต่อเนื่องอีกชนิดหนึ่งที่ถูกใช้งานมาก
การแจกแจงไคกำลังสองคือการแจกแจงผลรวมกำลังสองของการแจกแจงแบบปกติ
การแจกแจงไคกำลังสองเป็นการแจกแจงที่ถูกใช้งานอย่างกว้างขวางในทางวิทยาศาสตร์ เพราะเป็นพื้นฐานที่ใช้ในการทดสอบไคกำลังสอง (χ²检验, Chi-squared test) ที่เอาไว้พิจารณาทดสอบความสมเหตุสมผลของผลการทดลองต่างๆ
ลักษณะการแจกแจงดังกล่าวเกิดขึ้นเมื่อมีการสุ่มค่าใดๆที่มีการแจกแจงเป็นแบบปกติมาตรฐาน (คือที่ μ=0 และ σ=1) แล้วหาผลบวกกำลังสองของค่านั้น
ให้ ti เป็นค่าที่ได้จากการสุ่มที่มีการแจกแจงแบบปกติ k ครั้ง หาผลรวมกำลังสองค่าที่ได้นี้
🧹(18.1)
แล้วค่า x ในที่นี้จะมีการแจกแจงความหนาแน่นของความน่าจะเป็นเป็นการแจกแจงไคกำลังสอง
รูปทั่วไปของการแจกแจงไคกำลังสองเป็นดังนี้
🧹(18.2)
โดย Γ ก็คือฟังก์ชันแกมมา
🧹(18.3)
พารามิเตอร์ของการแจกแจงไคกำลังสองมีแค่ตัวเดียวคือค่า k ซึ่งคือจำนวนครั้งที่ทำการสุ่ม ในที่นี้มักเรียกว่าเป็นองศาเสรี (自由度, degree of freedom)
ลองดูตัวอย่างการสุ่มจริงด้วยไพธอน โดยลองทำการสุ่มค่าโดยมีการแจกแจงแบบปกติ 4 ครั้ง แล้วคำนวณผลรวมของค่ากำลังสอง ทำแบบนี้ซ้ำๆสักหมื่นครั้ง เอาผลที่ได้มาวาดแสดงการแจกแจงเป็นฮิสโทแกรม
import random
import matplotlib.pyplot as plt
k = 4 # จำนวนค่าที่จะสุ่ม
n = 10000 # จำนวนครั้งที่จะลองทำซ้ำ
x = [] # ลิสต์เก็บค่าผลรวมที่สุ่มได้
for i in range(n):
xi = 0 # ผลรวมของค่าที่สุ่มได้
for j in range(k):
# สุ่มแบบปกติแล้วคำนวณค่ากำลังสอง แล้วบวกเพิ่มไป ทำทั้งหมด k ครั้ง
xi += random.gauss(0,1)**2
x += [xi] # เก็บค่าผลรวมของการสุ่มที่ได้
# วาดฮิสโทแกรม
plt.hist(x,60,fc='#fad356',ec='k')
plt.show()ผลที่ได้จะเป็นฮิสโทแกรมที่แสดงการแจกแจงให้เห็นในลักษณะแบบนี้
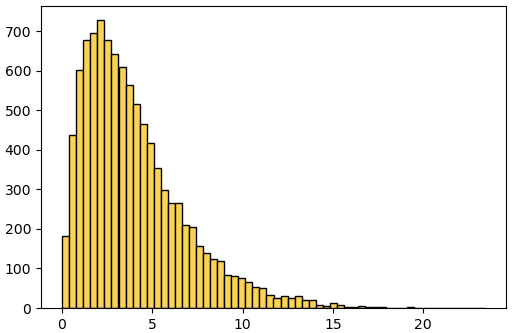
ค่าที่สุ่มนั้นถูกสุ่มให้มีการแจกแจงเป็นแบบปกติ แต่พอเอาค่ามายกกำลังสองก็จะไม่ใช่การแจกแจงแบบปกติ
ลองดูภาพเคลื่อนไหวนี้เพื่อเปรียบเทียบระหว่างระหว่างผลรวมของค่าที่สุ่มได้เฉยๆกับผลรวมของค่ากำลังสอง
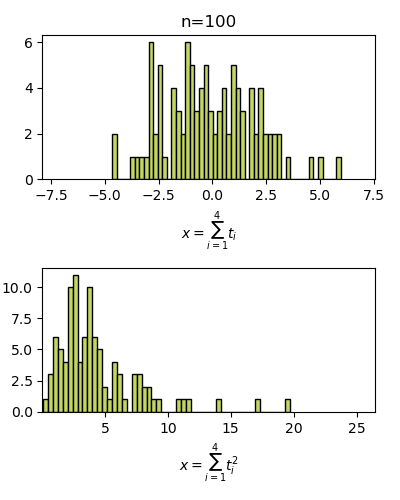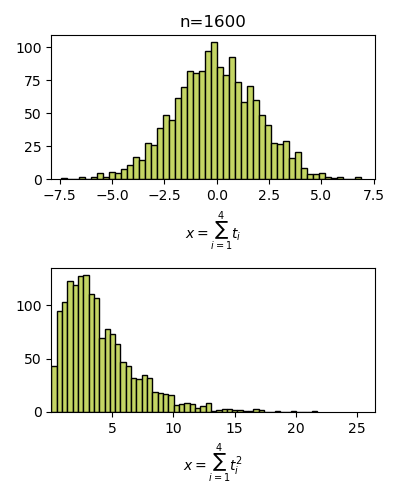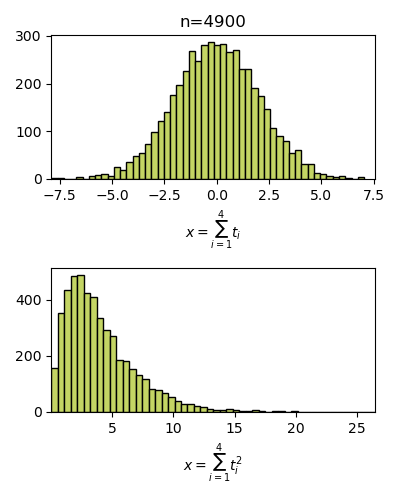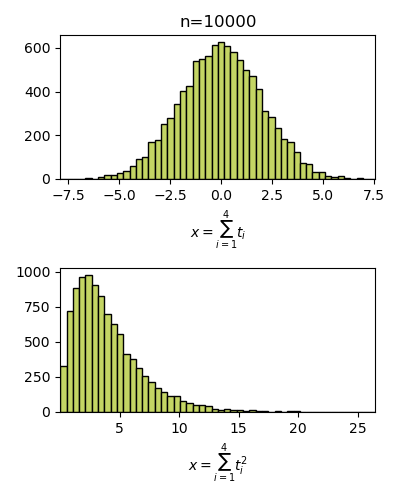
จะเห็นว่าผลรวมธรรมดาจะไม่ต่างจากเดิมนัก จุดสุดสูงสุดยังไงก็เป็น 0 แต่ถ้ายกกำลังสอง จะทำให้ค่าที่ได้ทั้งหมดเป็นบวก และมีแนวโน้มที่จะมีจุดสูงสุดของการแจกแจงเป็นค่าหนึ่งที่มากกว่า 0
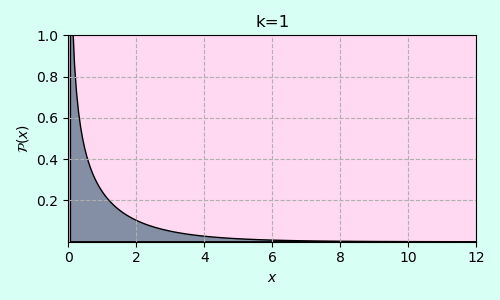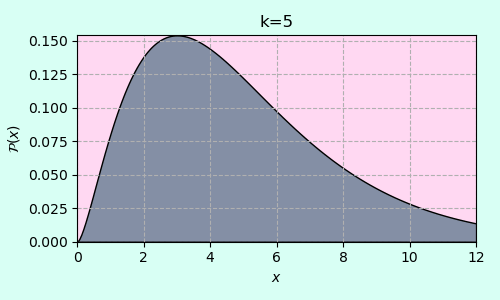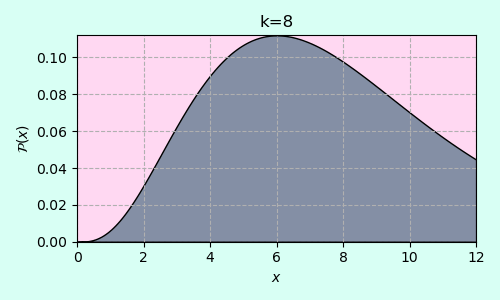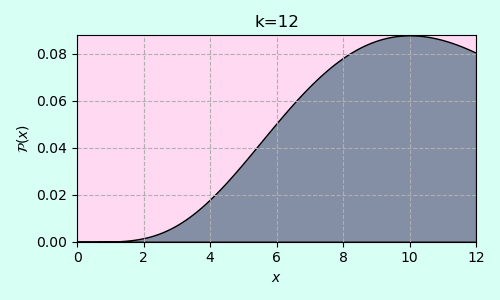
กราฟการแจกแจงไคกำลังสองโดยไล่ตั้งแต่ k=1 ไปจนถึง k=12
จุดสูงสุดและค่าคาดหมายการแจกแจงไคกำลังสอง
กราฟตัวอย่างการแจกแจงไคกำลังสองที่ k เป็น 1 ไปจนถึง 7
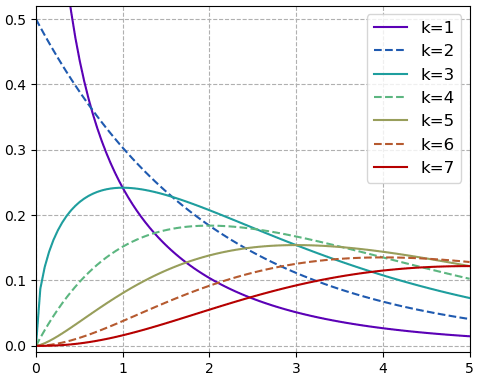
จะเห็นว่าเมื่อ k มากกว่า 2 กราฟจะมีจุดสูงสุด (ฐานนิยม) อยู่ ซึ่งตำแหน่งจุดสูงสุดนั้นคือ
🧹(18.4)
แต่ถ้า k เป็น 2 ลงมา จุดสูงสุดจะอยู่ที่ x=0
ส่วนค่าคาดหมายก็เท่ากับค่า k
🧹(18.5)
ความแปรปรวนคือ
🧹(18.6)
ความสัมพันธ์ระหว่างการแจกแจงไคกำลังสองกับการแจกแจงแกมมา
ความจริงแล้วการแจกแจงไคกำลังสองก็คือการแจกแจงแกมมาชนิดหนึ่งนั่นเอง
พิจารณาสมการการแจกแจงแกมมาดังที่ได้เขียนถึงไปในบทที่ ๑๖
🧹(18.7)
จะเห็นว่าในสมการนี้หากแทน ν ด้วย k/2 และแทน β ด้วย 1/2 จะกลายเป็นการแจกแจงไคกำลังสอง
ฉะนั้นจริงๆแล้วการแจกแจงไคกำลังสองก็ถือเป็นแค่กรณีพิเศษแบบหนึ่งของการแจกแจงแกมมา
ความน่าจะเป็นสะสมของการแจกแจงไคกำลังสอง
การแจกแจงไคกำลังสองมักถูกนำไปใช้เพื่อพิสูจน์ว่าสมมุติฐานที่คิดไว้นั้นมีโอกาสเกิดขึ้นแค่ไหน โดยพิจารณาจากการแจกแจงความน่าจะเป็นสะสมตั้งแต่ x=0 ไปจนถึงตรงค่า x ที่พิจารณา ดังนั้นจึงมีความสำคัญที่จะพูดถึงการแจกแจงความน่าจะเป็นสะสม
การแจกแจงไคกำลังสองจะเริ่มจากที่ x เป็น 0 และมีค่าไปเรื่อยๆจนถึง x เป็นอนันต์ โดยจะลดลงเรื่อยๆ ยิ่งค่า x มากก็ยิ่งมีโอกาสเกิดขึ้นน้อยลงเรื่อยๆ โดยโอกาสที่ x จะได้ค่ามากถึงค่าเท่านั้นขึ้นไปเป็นเท่าไหร่ขึ้นอยู่กับการแจกแจงความน่าจะเป็นสะสม
ฟังก์ชันแจกแจงความน่าจะเป็นสะสมของการแจกแจงไคกำลังสองคือ
🧹(18.8)
โดย γ ในที่นี้คือฟังก์ชันแกมมาแบบไม่สมบูรณ์ (不完全Γ函数, incomplete gamma function)
🧹(18.9)
ตารางแสดงตำแหน่งค่า a ที่มีความน่าจะเป็นรวมฝั่งขวาเป็นค่าต่างๆ
| k |
(คือความน่าจะเป็นรวมของส่วนที่ค่า x > a) |
||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.95 | 0.90 | 0.80 | 0.70 | 0.50 | 0.30 | 0.20 | 0.10 | 0.05 | 0.01 | 0.001 | 1 | 0.004 | 0.02 | 0.06 | 0.15 | 0.46 | 1.07 | 1.64 | 2.71 | 3.84 | 6.63 | 10.83 |
| 2 | 0.10 | 0.21 | 0.45 | 0.71 | 1.39 | 2.41 | 3.22 | 4.61 | 5.99 | 9.21 | 13.82 |
| 3 | 0.35 | 0.58 | 1.01 | 1.42 | 2.37 | 3.66 | 4.64 | 6.25 | 7.81 | 11.34 | 16.27 |
| 4 | 0.71 | 1.06 | 1.65 | 2.20 | 3.36 | 4.88 | 5.99 | 7.78 | 9.49 | 13.28 | 18.47 |
| 5 | 1.14 | 1.61 | 2.34 | 3.00 | 4.35 | 6.06 | 7.29 | 9.24 | 11.07 | 15.09 | 20.52 |
| 6 | 1.63 | 2.20 | 3.07 | 3.83 | 5.35 | 7.23 | 8.56 | 10.64 | 12.59 | 16.81 | 22.46 |
| 7 | 2.17 | 2.83 | 3.82 | 4.67 | 6.35 | 8.38 | 9.80 | 12.02 | 14.07 | 18.48 | 24.32 |
| 8 | 2.73 | 3.49 | 4.59 | 5.53 | 7.34 | 9.52 | 11.03 | 13.36 | 15.51 | 20.09 | 26.12 |
| 9 | 3.32 | 4.17 | 5.38 | 6.39 | 8.34 | 10.66 | 12.24 | 14.68 | 16.92 | 21.67 | 27.88 |
| 10 | 3.94 | 4.87 | 6.18 | 7.27 | 9.34 | 11.78 | 13.44 | 15.99 | 18.31 | 23.21 | 29.59 |
ภาพประกอบเสริมความเข้าใจความหมายในตารางนี้ เทียบกราฟกรณี k เป็น 2,4,6 พื้นที่สีชมพูคือส่วนทางขวาที่มีความน่าจะเป็นรวมเป็นค่า P เท่ากับที่แสดงในขณะนั้น
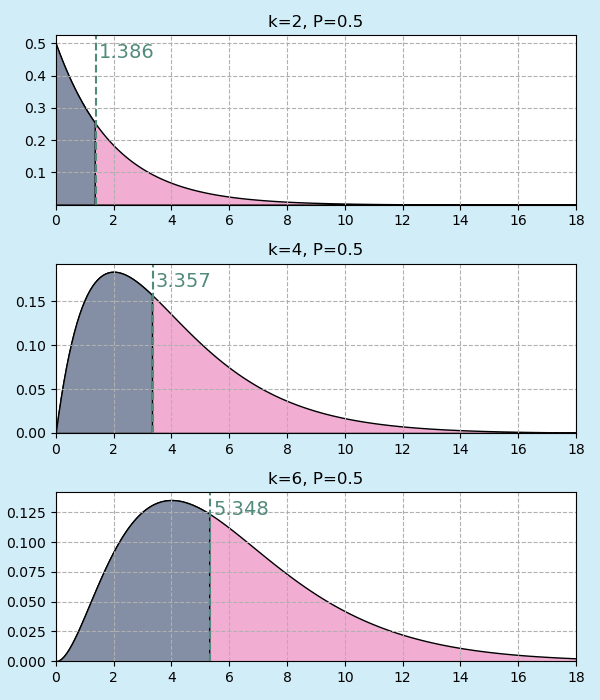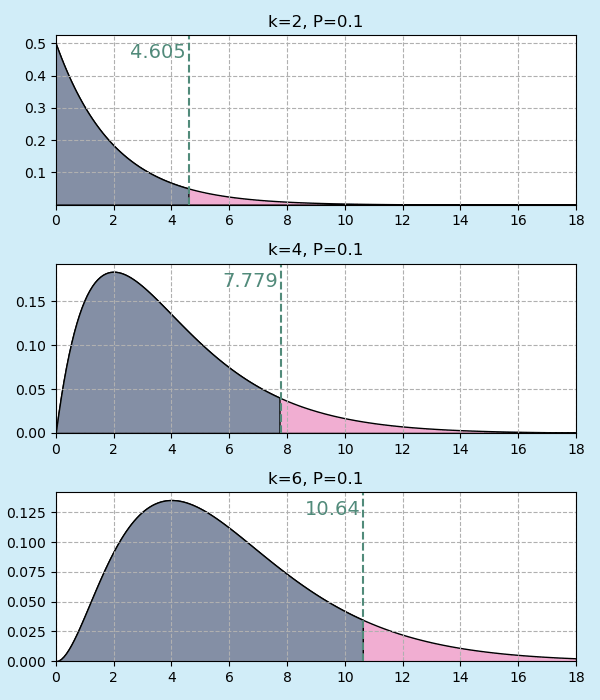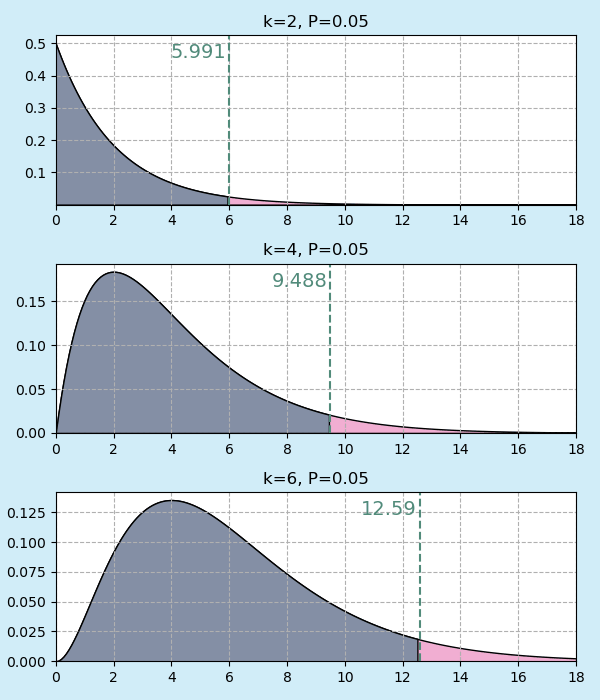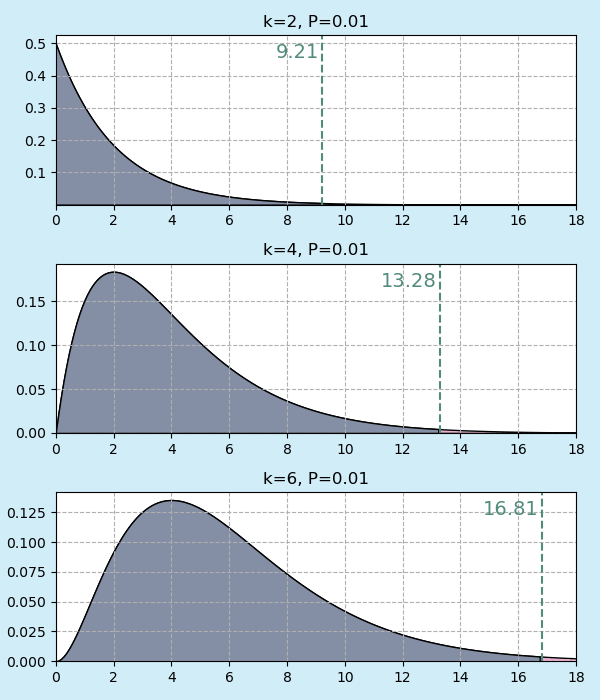
เส้นสีเขียวและตัวเลขสีเขียวคือค่า a
ยิ่งค่า a มากก็ยิ่งทำให้พื้นที่ส่วนฝั่งขวาลดลง โดยจะต่างกันไปขึ้นอยู่กับ k ด้วย
รายละเอียดกว่านั้นเกี่ยวกับเรื่องการทดสอบสมมุติฐานหรือช่วงความเชื่อมั่นนั้นในที่นี้จะไม่ได้เขียนถึง เพราะจะเน้นที่การแจกแจงความน่าจะเป็นเป็นหลัก สามารถอ่านเพิ่มเติมเพื่อทำความเข้าใจต่อได้ในเรื่องของการทดสอบไคกำลังสอง ซึ่งอยู่ในขอบเขตเนื้อหาวิชาสถิติ
บทถัดไป >> บทที่ ๑๙