ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๗: การแจกแจงวิชาร์ตกับเมทริกซ์ความเที่ยงตรงของการแจกแจงแบบปกติหลายตัวแปร
เขียนเมื่อ 2020/09/07 19:41
แก้ไขล่าสุด 2025/03/15 18:23
ต่อจาก บทที่ ๑๖
ในบทนี้เป็นเรื่องของการแจกแจงวิชาร์ต (威沙特分布, Wishart distribution) ซึ่งเป็นการแจกแจงความน่าจะเป็นของเมทริกซ์ความเที่ยงตรงของการแจกแจงแบบปกติหลายตัวแปร
เมทริกซ์ความเที่ยงตรง
ดังที่เคยเขียนถึงไปในบทที่ ๑๓ และบทที่ ๑๕ สมการการแจกแจงแบบปกติมักเขียนในลักษณะนี้
โดย Σ คือเมทริกซ์ความแปรปรวนร่วมเกี่ยว
แต่ในการคำนวณบางกรณีจะเป็นการสะดวกกว่าถ้าเขียนในรูปของเมทริกซ์ผกผันของ Σ
Λ นี้เรียกว่าเป็นเมทริกซ์ความเที่ยงตรง (精度矩阵, precision matrix) ซึ่งเป็นส่วนกลับของเมทริกซ์ความแปรปรวนร่วมเกี่ยว กล่าวคือ Σ ถ้ายิ่งมีตัวเลขมากยิ่งหมายถึงว่าค่ามีการแจกแจงมาก แต่ถ้า Λ มากจะหมายถึงค่ามีการแจกแจงน้อย ค่ามีความเที่ยงตรงมาก
เมื่อแทนด้วย Λ การแจกแจงแบบปกติหลายตัวแปรจะเขียนเป็นแบบนี้
เวลาเขียนแทนด้วย แบบนี้ปกติค่าตัวที่สองที่ใส่จะต้องเป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว ดังนั้นในกรณีที่ใช้เป็นเมทริกซ์ความเที่ยงตรงมักจะเขียนในรูปผกผัน Λ-1 แบบนี้ ไม่ใช่ Λ เฉยๆ
การแจกแจงวิชาร์ต
การแจกแจงวิชาร์ตมีรูปทั่วไปเป็นดังนี้
ที่เป็นตัวหนา ได้แก่ V และ Λ เป็นเมทริกซ์ขนาด m×m (โดย m เป็นจำนวนตัวแปร)
ถ้าเมทริกซ์ล้อมด้วย | | เช่น |V| และ |Λ| จะหมายถึงดีเทอร์มิแนนต์
ส่วน tr หมายถึงผลบวกค่าทั้งหมดในแนวทแยงของเมทริกซ์นั้น
พารามิเตอร์มี 2 ตัวคือ
- คือค่า องศาเสรี (自由度, degree of freedom) เทียบเท่าได้กับ ν/2 ในการแจกแจงแกมมา
- คือ เมทริกซ์สเกลปรับสเกล (尺度矩陣, scale matrix) มีขนาดเท่ากับเมทริกซ์ Λ
Γm เป็นฟังก์ชันแกมมาแบบหลายตัวแปร
จะเห็นว่าค่อนข้างยุ่ง แต่ก้อนนี้เป็นแค่ส่วนหนึ่งของค่าคงที่ซึ่งมีไว้หารเพื่อให้ผลรวมความน่าจะเป็นทั้งหมดเป็น 1 เท่านั้น ในที่นี้ไม่จำเป็นต้องสนใจก็ได้
ค่าต่างๆที่ไม่ได้เกี่ยวกับ Λ จะดึงมารวมไว้ใน แล้วเขียนใหม่ได้ดังนี้
ถ้า m=1 หมายถึงเป็นมิติเดียว V และ Λ ก็จะกลายเป็นเลขตัวเดียว แล้วหากเปลี่ยน เป็น และให้ค่าตัวเดียวใน V เป็น 1/β การแจกแจงนี้ก็จะกลายมาเป็นการแจกแจงแกมมา
ขอยกการแจกแจงแกมมามาเทียบให้ดูตรงนี้
การแจกแจงวิชาร์ตจึงถือเป็นการแจกแจงแกมมาที่ขยายเพิ่มเป็นหลายมิติเพื่อใช้กับการแจกแจงความน่าจะเป็นแบบปกติหลายตัวแปร
ค่าคาดหมายของการแจกแจงของเมทริกซ์ความเที่ยงตรงของการแจกแจงวิชาร์ตมีค่าเป็น
ค่าของเมทริกซ์ความเที่ยงตรงที่มีความน่าจะเป็นในการแจกแจงสูงสุดคือ
การแจกแจงความน่าจะเป็นของเมทริกซ์ความเที่ยงตรง
ต่อไปจะพิจารณาการแจกแจงความน่าจะเป็นของเมทริกซ์ความเที่ยงตรง Λ เช่นเดียวกับที่ทำกับค่าพารามิเตอร์ความเที่ยงตรง α ในบทที่แล้ว
วิธีการโดยรวมๆแล้วก็จะคล้ายๆกัน แค่ปริมาณต่างๆที่พิจารณานั้นเป็นเมทริกซ์ ไม่ใช่เลขตัวเดียว การคำนวณคูณกันก็ต้องคูณแบบเมทริกซ์
ความน่าจะเป็นก่อนหน้าเมื่อไม่มีข้อมูลก็สามารถให้เริ่มจากค่าคงที่ ซึ่งจะได้จากกรณีที่ และ Λ เป็นเมทริกซ์ที่ค่าข้างในมีค่าเล็กๆเข้าใกล้ 0
ให้ เป็นข้อมูล m มิติ (m ตัวแปร) ที่ได้จากการสุ่มแบบปกติหลายตัวแปร ฟังก์ชันควรจะเป็นก็จะได้เป็น
แล้วก็จะคำนวณความน่าจะเป็นภายหลังได้เป็นการแจกแจงวิชาร์ต
และถ้าหากมีข้อมูล n ตัวก็จะได้การแจกแจงวิชาร์ตดังนี้
กรณีที่มีการแจกแจงก่อนหน้าเป็น และ
การแจกแจงความน่าจะเป็นภายหลังก็จะได้เป็น
ต่อไปเป็นตัวอย่างโค้ด ให้สร้างข้อมูลสองมิติที่ทำการสุ่มแบบปกติหลายตัวแปร แล้วลองหาการแจกแจงความน่าจะเป็น
import numpy as np
ν0 = 5
# เมทริกซ์ความแปรปรวนตั้งต้น
Σ0 = np.array([[0.5,0.1],
[0.1,0.5]])
# เมทริกซ์ความแปรปรวนจริงๆที่ต้องการหา
Σ = np.array([[5.,1],
[1,2.]])
μ = np.array([0,0])
x = np.random.multivariate_normal(μ,Σ,3600)
m = len(Σ) # จำนวนมิติ
for i in range(11):
n = (6*i)**2 # จำนวนจุดข้อมูล
# คำนวณค่า ν และเมทริกซ์ V ใหม่ในแต่ละรอบ
ν = ν0+n
V = np.linalg.inv(np.dot((x[:n]-μ).T,(x[:n]-μ))+Σ0)
Σ_max = np.linalg.inv((ν-m-1)*V) # จุดที่ความน่าจะเป็นสูงที่สุด
print(f'ν = {ν}\nV = {V}\nΣ = {Σ_max}')ผลที่ได้
ν = 5
V = [[ 2.08333333 -0.41666667]
[-0.41666667 2.08333333]]
Σ = [[0.25 0.05]
[0.05 0.25]]
ν = 41
V = [[0.0055187 0.00104572]
[0.00104572 0.01859767]]
Σ = [[ 4.81982819 -0.2710123 ]
[-0.2710123 1.4302435 ]]
ν = 149
V = [[ 0.00176174 -0.00041632]
[-0.00041632 0.00410707]]
Σ = [[3.98321883 0.40377066]
[0.40377066 1.70861973]]
ν = 329
V = [[ 0.00068913 -0.00027996]
[-0.00027996 0.00172312]]
Σ = [[4.76578006 0.77430338]
[0.77430338 1.90599849]]
ν = 581
V = [[ 0.00036217 -0.00017873]
[-0.00017873 0.00095164]]
Σ = [[5.26499485 0.98885953]
[0.98885953 2.00375218]]
ν = 905
V = [[ 0.00024671 -0.00011678]
[-0.00011678 0.00061443]]
Σ = [[4.93794367 0.93853582]
[0.93853582 1.98272111]]
ν = 1301
V = [[ 1.72833326e-04 -7.97935605e-05]
[-7.97935605e-05 4.19152283e-04]]
Σ = [[4.88708963 0.93034989]
[0.93034989 2.0151434 ]]
ν = 1769
V = [[ 1.22722015e-04 -5.43669747e-05]
[-5.43669747e-05 3.06883104e-04]]
Σ = [[5.00706708 0.88704489]
[0.88704489 2.00231735]]
ν = 2309
V = [[ 9.57755868e-05 -4.67090851e-05]
[-4.67090851e-05 2.38106922e-04]]
Σ = [[5.00678507 0.98217367]
[0.98217367 2.01391784]]
ν = 2921
V = [[ 7.47142508e-05 -3.57389306e-05]
[-3.57389306e-05 1.87296108e-04]]
Σ = [[5.04752753 0.9631446 ]
[0.9631446 2.01350814]]
ν = 3605
V = [[ 6.11264567e-05 -2.97188289e-05]
[-2.97188289e-05 1.53627692e-04]]
Σ = [[5.01329716 0.96980772]
[0.96980772 1.99472562]]ตัวแปรที่แจกแจงในการแจกแจงวิชาร์ตคือเมทริกซ์ความเที่ยงตรง แต่ในที่นี้เพื่อให้เห็นภาพง่ายจึงแสดงเป็นเมทริกซ์ความแปรปรวนเป็นหลัก เวลาคำนวณก็ใช้ np.linalg.inv เพื่อคำนวณเมทริกซ์ผกผัน
วาดภาพเคลื่อนไหวแสดงการแจกแจงที่เปลี่ยนไปตามเวลาได้แบบนี้
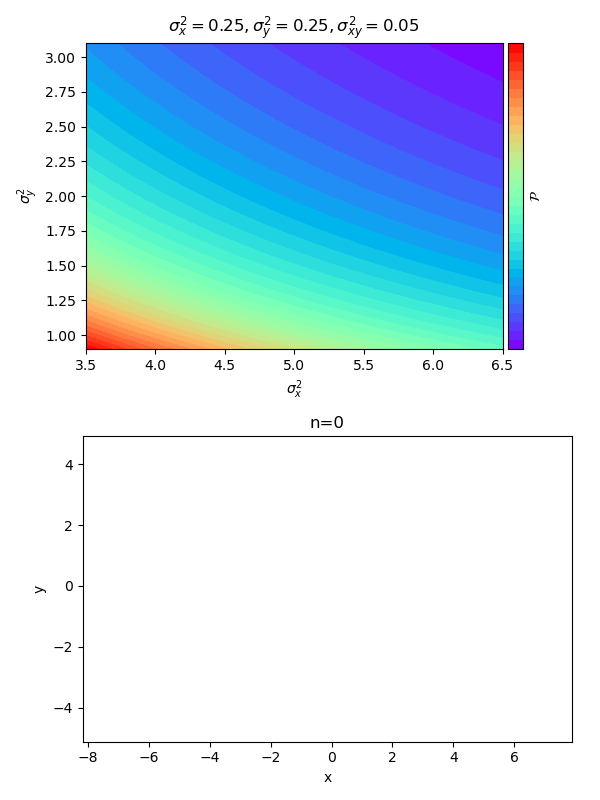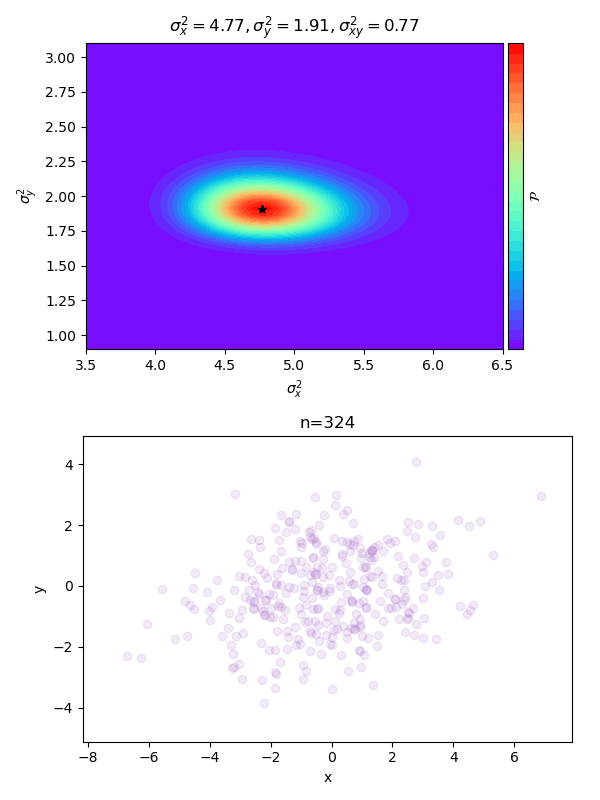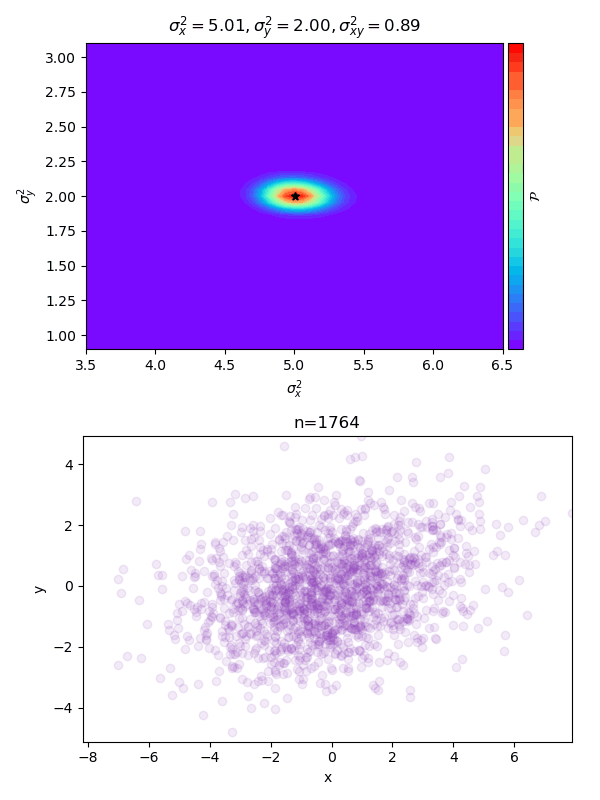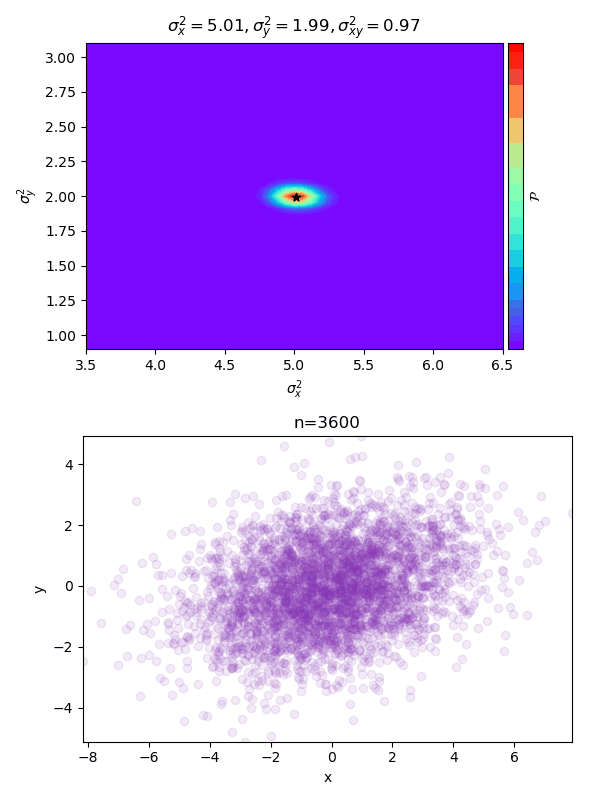
ภาพด้านบนคือค่าความหนาแน่นความน่าจะเป็นที่ค่า ต่างๆที่ สูงสุด โดยสีแดงคือค่าสูงสีม่วงคือค่าน้อย ค่าทั้ง 3 ตัวที่แสดงด้านบนคือค่าที่ตำแหน่งสูงสุด จุดรูปดาวแสดงตำแหน่งที่ค่าสูงสุด
ภาพด้านล่างแสดงการแจกแจงของจุดข้อมูลที่มี ทั้งหมด n จุด
ยิ่งใส่จุดข้อมูลมาก การแจกแจงค่า ที่คำนวณได้ก็จะยิ่งมากองอยู่ใกล้จุด ซึ่งเป็นค่าจริงๆของการแจกแจงนี้
บทถัดไป >> บทที่ ๑๘