ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๓: ความแปรปรวนร่วมเกี่ยวและการแจกแจงแบบปกติหลายตัวแปร
เขียนเมื่อ 2020/08/31 13:55
แก้ไขล่าสุด 2022/07/10 21:05
ต่อจาก บทที่ ๑๒ ซึ่งได้อธิบายถึงการแจกแจงแบบปกติตัวแปรเดียวไปแล้ว
ในบทนี้จะยังคงเป็นเรื่องของการแจกแจงแบบปกติ แต่ขยายมาเป็นการแจกแจงปกติหลายตัวแปร
ที่จริงเนื้อหาในบทนี้จะใกล้เคียงกับบทความที่เคยเขียนไปในบทความก่อนหน้านี้คือ
- วิเคราะห์ความสัมพันธ์ระหว่างตัวแปรจากค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
- การสร้างค่าสุ่มด้วยการแจกแจงแบบปกติหลายตัวแปร
เพียงแต่วิธีการเล่าจะต่างกัน ดังนั้นหากอ่านหน้านี้ไม่เข้าใจสามารถอ่านใน 2 หน้านั้นแทนได้ จะมีการอธิบายรายละเอียดบางส่วนมากกว่า
การแจกแจงแบบปกติตัวแปรเดียว
ในบทที่ผ่านๆมาใช้มอดูล random เป็นหลักเพื่อความเข้าใจง่าย แต่สำหรับในบทนี้ การแจกแจงปกติหลายตัวแปรไม่มีในมอดูล random จำเป็นต้องใช้ numpy
ก่อนอื่นขอเริ่มทวนจากเรื่องการแจกแจงแบบปกติตัวแปรเดียวซึ่งอธิบายในบทที่แล้ว นั่นคือหากมีตัวแปรตัวเดียวคือ x ซึ่งแจกแจงแบบปกติโดยมี μ เป็นจุดกึ่งกลาง (และก็คือค่าเฉลี่ย) ของการกระจาย และ σ คือส่วนเบี่ยงเบนมาตรฐานของการกระจาย (และ σ2 คือความแปรปรวน) ฟังก์ชันความหนาแน่นของความน่าจะเป็นคือ
เช่นเดียวกับที่ random.gauss() ในมอดูล random ที่กล่าวถึงในบทที่แล้ว การสุ่มค่าตัวเลขโดยมีการแจกแจงแบบปกตินั้นใน numpy สามารถทำได้โดยใช้ฟังก์ชัน np.random.normal() โดยใส่ np.random.normal(μ,σ,จำนวนที่ต้องการสุ่ม)
รายละเอียดเพิ่มเติมเกี่ยวกับฟังก์ชันสุ่มเบื้องต้นใน numpy อ่านได้ใน เนื้อหา numpy & matplotlib เบื้องต้น บทที่ ๑๕
ตัวอย่าง ลองสร้างค่าแบบสุ่มแล้วมาวาดฮิสโทแกรมแสดงการแจกแจง แล้วก็คำนวณค่าเฉลี่ยกับส่วนเบี่ยงเบนมาตรฐานและความแปรปรวน
import numpy as np
import matplotlib.pyplot as plt
μ = 10
σ = 3
x = np.random.normal(μ,σ,10000)
plt.hist(x,50,color='c',ec='m')
plt.show()
print('ค่าเฉลี่ย',x.mean()) # ได้ 9.942270432427566
print('ส่วนเบี่ยงเบนมาตรฐาน',x.std()) # ได้ 2.9856620000603917
print('ความแปรปรวน',x.var()) # ได้ 8.914177578604619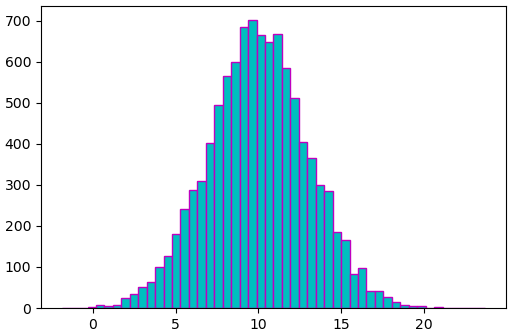
จะได้เห็นว่าได้ค่าการแจกแจงเป็นระฆังคว่ำที่มีจุดกึ่งกลาง μ = 10 และส่วนเบี่ยงเบนมาตรฐาน σ = 3 และเมื่อคำนวณค่าเฉลี่ยกับส่วนเบี่ยงเบนมาตรฐานและความแปรปรวนของข้อมูลที่สุ่มได้ก็จะออกมาได้ใกล้เคียง
หากมีตัวแปร 2 ตัวขึ้นไปซึ่งแจกแจงแบบปกติโดยเป็นอิสระจากกัน แบบนี้ก็ถือเป็นการแจกแจงแบบปกติตัวแปรเดียวเช่นกัน แค่สุ่มหลายตัวแปรแต่ไม่ได้เกี่ยวข้องกัน
เช่นลองสุ่มค่า x และ y ซึ่งต่างก็แจกแจงแบบปกติ แล้วเอามาวาดแสดงการแจกแจง
μ_x = 7
σ_x = 5
x = np.random.normal(μ_x,σ_x,2000)
μ_y = 2
σ_y = 3
y = np.random.normal(μ_y,σ_y,2000)
plt.axes(aspect=1,xlabel='x',ylabel='y')
plt.scatter(x,y,color='#5233b8',ec='k',alpha=0.1)
plt.show()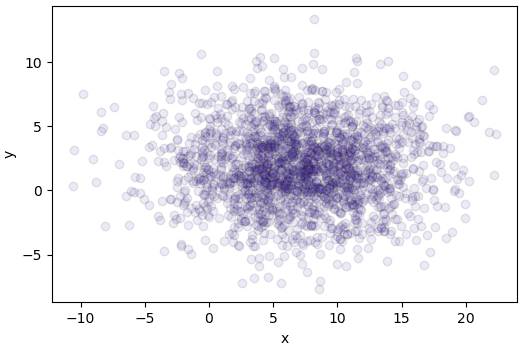
จะเห็นว่ามีการแจกแจงแบบเกาส์อย่างสม่ำเสมอทั้งในแกน x และ y
เมทริกซ์ความแปรปรวนร่วมเกี่ยว
ในธรรมชาติค่าอะไรบางอย่างที่เกิดขึ้นแบบสุ่มมักจะมีความสัมพันธ์กับค่าสุ่มอีกค่า ไม่ได้ต่างคนต่างสุ่มแยกเป็นอิสระไม่เกี่ยวข้องกันโดยทั้งหมด
การสุ่มค่าแบบปกติพร้อมกันหลายๆตัวโดยพิจารณาถึงความสัมพันธ์ระหว่างค่าแต่ละตัวไปด้วยนั้นจะเรียกว่าการแจกแจงแบบปกติหลายตัวแปร (多元正态分布, multivariate normal distribution)
หากมีชุดข้อมูลของตัวแปรสุ่ม n ตัว
และแต่ละตัวในนี้มีการแจกแจงแบบปกติหลายตัวแปร จะมีฟังก์ชันการแจกแจงความหนาแน่นเป็นดังนี้
โดย คือจุดกึ่งกลางการแจกแจงของแต่ละค่า
ในที่นี้ชื่อตัวแปรใช้ลูกษรข้างบนเพื่อใช้แสดงว่าเป็นปริมาณที่มีหลายตัว ไม่ได้มีแค่ตัวเดียว
ส่วน Σ คือเมทริกซ์ เรียกว่าเป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว (协方差矩阵, covariance matrix) เป็นเมทริกซ์ n×n ที่เขียนค่าความแปรปรวนร่วมเกี่ยว (协方差, covariance) ซึ่งแสดงความสัมพันธ์ระหว่างค่าของแต่ละตัวในชุดข้อมูล
ที่อยู่ในแทวทแยงคือ แสดงถึงความแปรปรวน (ส่วนเบี่ยงเบนมาตรฐานยกกำลังสอง) ของ xi
เรียกว่าเป็นความแปรปรวนร่วมเกี่ยว ระหว่างค่า 2 ตัวคือ xi กับ xj
ความแปรปรวนร่วมเกี่ยวคือค่าที่แสดงว่าตัวแปร 2 ตัวจะเปลี่ยนค่าไปโดยมีความสัมพันธ์กันอย่างไร ยิ่งค่ามากก็ยิ่งหมายความว่าทั้ง 2 ตัวสัมพันธ์กันมาก
หากมีตัวแปรสุ่ม 2 ตัวคือ xi และ xj ความแปรปรวนร่วมเกี่ยวระหว่าง xi กับ xj จะคำนวณได้เป็น
โดยในที่นี้ คือค่าคาดหมาย (ค่าเฉลี่ยของข้อมูลทั้งหมด) ของ xi
และจะเห็นว่าถ้าเป็นตัวแปรเดียวกัน ค่านี้ก็คือความแปรปรวนนั่นเอง
ดังนั้นอาจมองว่าความแปรปรวนคือสิ่งที่บอกถึงการแจกแจงภายในตัวแปรตัวเดียวเอง ส่วนความแปรปรวนร่วมเกี่ยวบอกถึงการแจกแจงที่สัมพันธ์ระหว่างตัวแปร 2 ตัว
เมทริกซ์ความแปรปรวนร่วมเกี่ยวจะมีลักษณะเป็นสมมาตรเสมอ เพราะทั้งแถวและหลักต่างก็ไล่เลียงค่าทั้ง n ตัวตามลำดับ และไม่ว่าจะเอาตัวไหนขึ้นก่อนก็มีค่าเท่ากัน
ส่วน |Σ| คือ ดีเทอร์มิแนนต์ (行列式, determinant) ของเมทริกซ์ Σ
ใน numpy มีฟังก์ชันสำหรับสุ่มโดยกระจายแบบปกติหลายตัวแปร คือ np.random.multivariate_normal() วิธีใช้คือ
np.random.multivariate_normal(μ,Σ,จำนวนที่ต้องการสุ่ม)ซึ่งจะเห็นว่าวิธีการใช้ดูคล้ายๆกับฟังก์ชัน np.random.normal() ซึ่งเอาไว้แจกแจงแบบปกติตัวเดียว แค่ μ ในที่นี้ไม่ใช่เลขค่าเดียวแต่เป็นหลายค่า ส่วนที่เดิมทีเป็นส่วนเบี่ยงเบนมาตรฐาน σ ก็เปลี่ยนเป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว Σ
การสุ่มนี้จะให้ค่าของทุกตัวแปรออกมาพร้อมกัน ผลที่ได้จะออกมาเป็นอาเรย์สองมิติ ขนาดเป็น [จำนวนที่ต้องการสุ่ม × จำนวนตัวแปร]
แต่ถ้าหากไม่ได้ใส่จำนวนที่ต้องการสุ่มไป ผลที่ได้จะออกมาเป็นอาเรย์หนึ่งมิติ ขนาดเท่ากับจำนวนตัวแปร
อนึ่ง จริงๆแล้วเมทริกซ์ความแปรปรวนร่วมเกี่ยวน่าจะเป็นสิ่งที่เทียบเท่ากับความแปรปรวน σ2 แต่ที่ใช้ใส่ใน np.random.normal() หรือ random.gauss() กลับเป็นส่วนเบี่ยงเบนมาตรฐาน σ ในขณะที่ np.random.multivariate_normal() กลับใส่เป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว ดังนั้นอาจต้องระวังจะใช้สับสน
ตัวอย่าง ลองสุ่มค่า x และ y ที่มีการแจกแจงแบบปกติโดยมีจุดกึ่งกลางการแจกแจงและเมทริกซ์ความแปรปรวนร่วมเกี่ยวเป็นดังนี้
μ = np.array([3,2])
Σ = np.array([[0.5,0.15],
[0.15,0.2]])
X = np.random.multivariate_normal(μ,Σ,2000)
print(X.shape) # ได้ (2000, 2)
x = X[:,0]
y = X[:,1]
plt.axes(aspect=1,xlabel='x',ylabel='y')
plt.scatter(x,y,color='#558812',ec='k',alpha=0.1)
plt.show()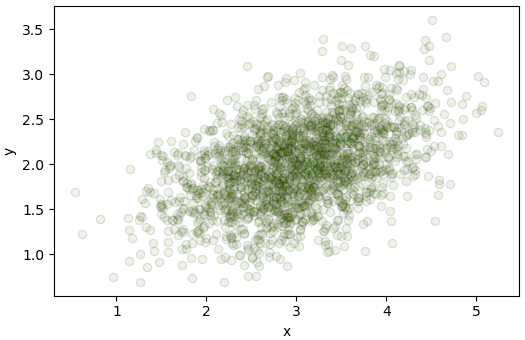
จะเห็นว่าได้ค่า x และ y ที่แจกแจงแบบเกาส์โดยมีลักษณะเอียง
เพื่อให้เห็นภาพของความแปรปรวนร่วมเกี่ยวมากขึ้น ลองดูอีกตัวอย่างโดยวาดหลายๆภาพที่มี (ความแปรปรวนร่วมเกี่ยวระหว่าง x และ y) ต่างกันออกไป
plt.figure(figsize=[6,9])
μ = np.array([0,0])
for i in range(6):
σ_xy = (i-2)*0.3
Σ = np.array([[1,σ_xy],
[σ_xy,1]])
X = np.random.multivariate_normal(μ,Σ,1000)
x = X[:,0]
y = X[:,1]
plt.subplot(3,2,1+i,aspect=1,title='$σ_{x,y}^2=%.3f$'%σ_xy)
plt.scatter(x,y,color='#a133b8',ec='k',alpha=0.1)
plt.tight_layout()
plt.show()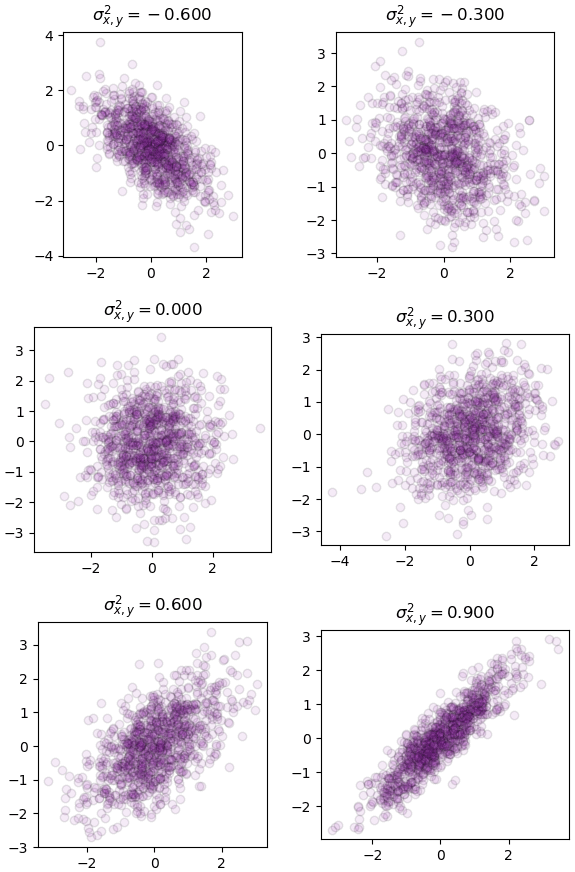
จากตัวอย่างน่าจะพอทำให้เห็นภาพขึ้นมาได้ว่าค่าความแปรปรวนร่วมเกี่ยวมีผลอย่างไรต่อการแจกแจง
ภาพกลางฝั่งซ้ายแสดงกรณีที่ค่านอกจากในแนวทแยงเป็น 0 ทั้งหมด แบบนี้แสดงว่าค่าแต่ละตัวไม่มีความเกี่ยวข้องกันเลย แบบนั้นการแจกแจงก็จะไม่ต่างไปจากกรณีที่ใช้แจกแจงแบบตัวแปรเดียวแยกกันทีละตัว
ต่อมาลองแสดงตัวอย่างการสุ่มจุดขึ้นมาพร้อมกันเป็นชุดหลายๆตัว เอาแต่ละตัวมาเรียงต่อกัน
หากเมทริกซ์ความแปรปรวนร่วมเกี่ยวเป็นเมทริกซ์แนวทแยง คือมีค่าแค่ในแนวทแยง แต่ละค่าจะสุ่มแบบแยกเป็นอิสระต่อกันหมดไม่เกี่ยวข้องกัน
μ = np.zeros(20)
Σ = np.eye(20)
for i in range(6):
plt.plot(np.random.multivariate_normal(μ,Σ),'o-')
plt.show()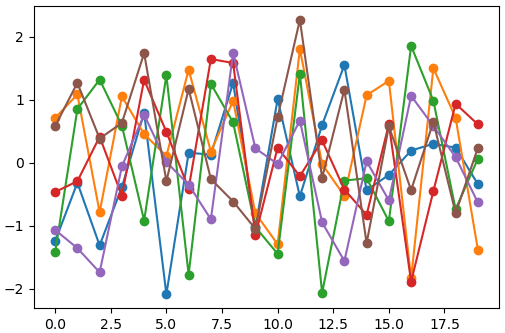
ถ้าเปลี่ยนมาใช้ค่าเดียวกันทั้งหมดเป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว แบบนั้นเท่ากับว่าทุกค่าจะเกี่ยวพันกันเท่ากันหมด ทำให้ได้ค่าเหมือนกันหมด
μ = np.zeros(20)
Σ = np.ones([20,20])
for i in range(6):
plt.plot(np.random.multivariate_normal(μ,Σ),'o-')
plt.show()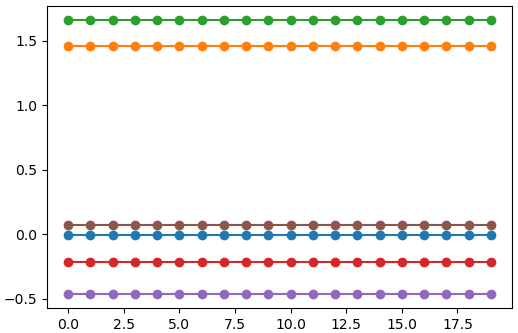
ลองเปลี่ยนเมทริกซ์ความแปรปรวนร่วมเกี่ยวให้มีค่าแนวทแยงมากกว่าเล็กน้อย จะทำให้ค่าแต่ละตัวต่างกันไปเล็กน้อย
μ = np.zeros(20)
Σ = np.ones([20,20]) + np.eye(20)/20
for i in range(6):
plt.plot(np.random.multivariate_normal(μ,Σ),'o-')
plt.show()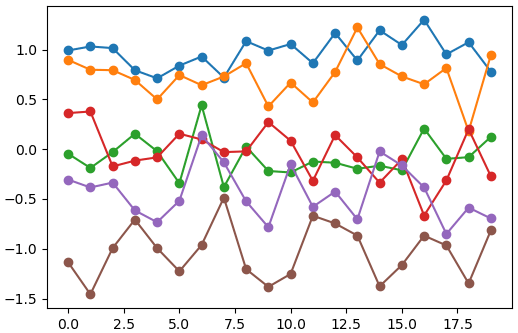
การสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวด้วยฟังก์ชันเคอร์เนล
ค่าที่เป็นอนุกรมเวลา (เช่นอุณหภูมิในแต่ละนาที) หรือแสดงค่าในตำแหน่งต่างๆกัน (เช่นอุณหภูมิที่ตำแหน่งต่างๆบนโต๊ะ) ค่าพวกนี้มักจะสัมพันธ์กับค่าที่ตำแหน่งหรือจุดเวลาใกล้ๆ กรณีแบบนี้เมื่อต้องการสร้างเมทริกซ์ความแปรปรวนร่วมอาจทำโดยใช้วิธีเคอร์เนล (kernel)
ให้ k(x1,k2) เป็นฟังก์ชันอะไรบางอย่างของตัวแปรสองตัวซึ่งเป็นค่าตำแหน่ง (หรือเวลา) เราสามารถสร้างค่าในเมทริกซ์ความแปรปรวนร่วมเกี่ยวขึ้นได้ในลักษณะนี้
ฟังก์ชัน k(x1,k2) ที่ใช้สร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวในลักษณะนี้มักเรียกว่าฟังก์ชันเคอร์เนล หรืออาจเรียกว่าเคอร์เนลเฉยๆ
โดยทั่วไปฟังก์ชันเคอร์เนลมักขึ้นกับระยะห่างระหว่าง 2 ค่า หรือก็คือ k เป็นฟังก์ชันขอ |x1-k2|
ตัวอย่างฟังก์ชันเคอร์เนลที่ใช้บ่อยคือเคอร์เนลกำลังสองเอ็กซ์โพเนนเชียล ซึ่งก็คือหน้าตาเหมือนฟังก์ชันเกาส์
แล้วจะได้เมทริกซ์ความแปรปรวนร่วมเกี่ยวเป็น
ในที่นี้ฟังก์ชันขึ้นอยู่กับพารามิเตอร์ 2 ตัว คือ a ซึ่งเป็นตัวกำหนดขนาดของความแปรปรวน และ σ ซึ่งเป็นตัวกำหนดว่าจะให้ค่าส่งผลไปถึงรอบข้างเป็นวงกว้างแค่ไหน
ตัวอย่าง ลองสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวขึ้นมาแล้วแสดงการแจกแจงของค่าภายในเมทริกซ์นี้โดยใช้สี
def kernel(x,a,σ):
x1,x2 = np.meshgrid(x,x)
return a**2*np.exp(-0.5*((x1-x2)/σ)**2)
x = np.arange(0,31)
Σ = kernel(x,2,4)
plt.imshow(Σ,cmap='cividis')
plt.colorbar(pad=0.01)
plt.show()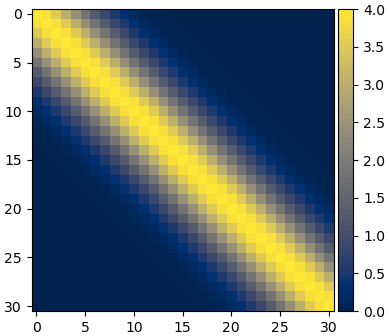
จะเห็นว่าได้เมทริกซ์ที่มีค่ามากในแนวทแยงแล้วค่าก็ค่อยๆลดลงเมื่อห่างออกจากแนวทแยง นั่นคือค่าของตัวใดๆจะเกี่ยวพันตัวข้างๆกันและยิ่งห่างออกไปยิ่งไม่เกี่ยวข้องกัน
ลองสุ่มค่าขึ้นมาโดยใช้เมทริกซ์ความแปรปรวนร่วมเกี่ยวนี้
μ = np.zeros(31)
y = np.random.multivariate_normal(μ,Σ,5)
plt.plot(x,y.T,'o-')
plt.show()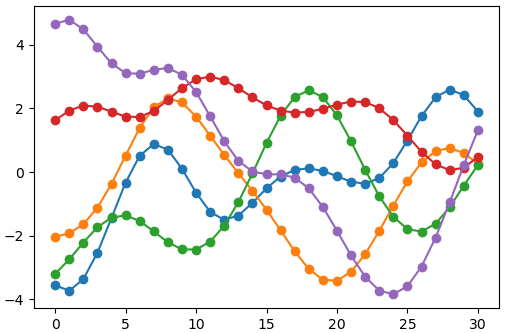
จะได้กราฟที่มีลักษณะเรียบๆ เพราะแต่ละตัวจะสัมพันธ์กับค่าที่อยู่ข้างเคียง
ฟังก์ชันเคอร์เนลอีกแบบที่เจอบ่อยคือ
ในที่นี้ δ คือเดลตาโครเนกเกอร์ (克罗内克δ, Kronecker delta) ซึ่งหมายความว่าจะเป็น 1 ถ้า x1 เท่ากับ x2 และจะเป็น 0 ถ้าไม่เท่า ผลก็คือจะได้เป็นเมทริกซ์แนวทแยงที่มีค่าแนวทแยงเป็น a และที่อื่นเป็น 0
ถ้าเขียนเป็นฟังก์ชันในไพธอนก็อาจเขียนได้แบบนี้
def kernel(x,a):
x1,x2 = np.meshgrid(x,x)
return a**2*(x1==x2)ลักษณะแบบนี้เรียกว่าเป็นสัญญาณรบกวนขาว (白噪声, white noise)
ฟังก์ชันเคอร์เนลอาจสร้างขึ้นโดยผสมเคอร์เนล 2 ชนิดเข้าด้วยกัน เช่น เคอร์เนลกำลังสองเอ็กซ์โพเนนเชียลรวมกับเคอร์เนลสัญญาณรบกวนขาว
ลองใช้เคอร์เนลแบบนี้สร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยว
def kernel(x,a,σ,a2):
x1,x2 = np.meshgrid(x,x)
return a**2*np.exp(-0.5*((x1-x2)/σ)**2) + a2**2*(x1==x2)
x = np.arange(0,31)
Σ = kernel(x,2,4,0.5)
plt.imshow(Σ,cmap='cividis')
plt.colorbar(pad=0.01)
plt.show()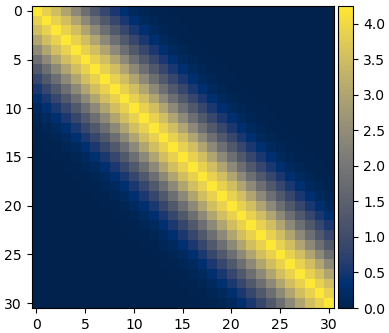
ค่าตรงแนวทแยงจะสูงเด่นขึ้นมากว่าเดิม
แล้วนำมาใช้สุ่มดูก็จะได้แบบนี้
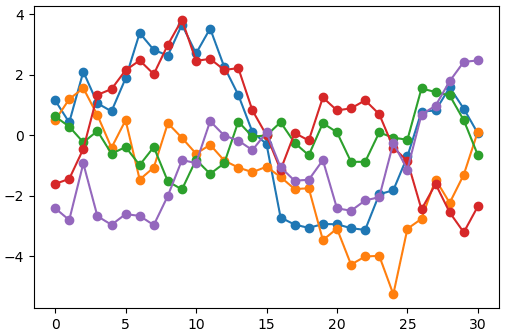
ผลที่ได้จะเห็นว่าค่าจะมีความต่อเนื่องจากค่าข้างเคียง แต่ไม่ได้เรียบเพราะมีส่วนของสัญญาณรบกวนขาวซึ่งทำให้เกิดความแปรปรวนของแต่ละจุดที่ไม่ได้เกี่ยวพันกับจุดอื่นๆ
ตัวอย่างเคอร์เนลแบบอื่นๆ
เคอร์เนลอีกแบบที่อาจเจอได้บ่อยคือเคอร์เนลแบบไซน์กำลังสองเอ็กซ์โพเนนเชียล (exp-sine-squared kernel)
ในที่นี้ τ คือคาบของการเปลี่ยนแปลง
ลองดูค่าของเมทริกซ์ความแปรปรวนร่วมเกี่ยวที่สร้างได้
def kernel(x,a,τ,λ):
x1,x2 = np.meshgrid(x,x)
return a**2*np.exp(-2*(np.sin((x1-x2)*np.pi/τ)/λ)**2)
x = np.arange(0,31)
Σ = kernel(x,a=2,τ=12,λ=2)
plt.imshow(Σ,cmap='cividis')
plt.colorbar(pad=0.01)
plt.show()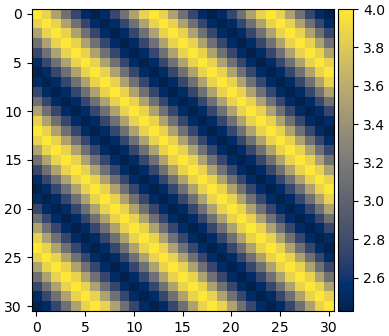
จะได้ค่าที่เปลี่ยนไปเป็นคาบตามระยะห่างจากแนวทแยง
แล้วนำมาใช้สุ่มดูจะได้ออกมาเป็นแบบนี้
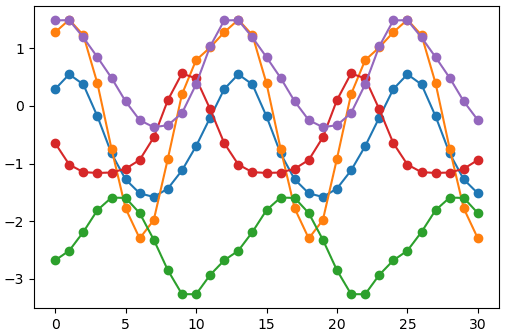
ผลที่ได้จะเห็นว่าค่าจะเปลี่ยนแปลงเป็นคาบ โดยคาบเท่ากับ τ
อีกตัวอย่างคือเคอร์เนลที่ทำให้เกิดการเปลี่ยนแปลงแบบเกือบเป็นคาบ (quasi-periodic) คือมีลักษณะที่จะวนกลับมาค่าใกล้เคียงเดิมอยู่เรื่อยๆเป็นคาบ แต่ไม่ได้เหมือนกันเสียทีเดียว ต่างออกไปทีละเล็กน้อย
ในที่นี้ τ คือคาบของการเปลี่ยนแปลง ส่วน σ เป็นตัวกำหนดว่าจะมีความสัมพันธ์กับตัวที่อยู่ไกลแค่ไหน ยิ่งค่ามากก็ยิ่งเห็นความแตกต่างในแต่ละคาบน้อยลง
ลองดูค่าของเมทริกซ์ความแปรปรวนร่วมเกี่ยวที่สร้างได้
def kernel(x,a,τ,λ,σ):
x1,x2 = np.meshgrid(x,x)
dx = x1-x2
return a**2*np.exp(-2*(np.sin(dx*np.pi/τ)/λ)**2-0.5*(dx/σ)**2)
x = np.arange(0,31)
Σ = kernel(x,a=2,τ=6,λ=2,σ=24)
plt.imshow(Σ,cmap='cividis')
plt.colorbar(pad=0.01)
plt.show()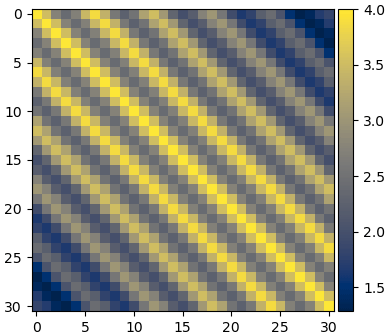
จะได้ค่าที่เปลี่ยนไปเป็นคาบตามระยะห่างจากแนวทแยงแค่ค่อยๆลดลงเรื่อยๆตามลำดับ
แล้วนำมาใช้สุ่มดูก็จะได้แบบนี้
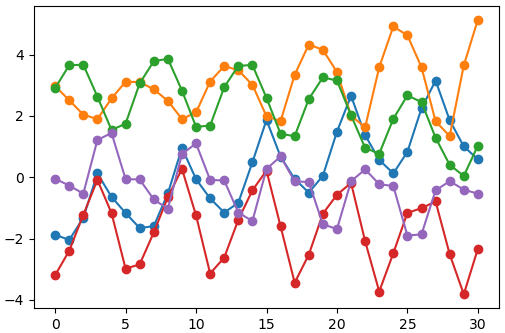
ผลที่ได้จะเห็นว่าค่าจะเปลี่ยนแปลงเป็นคาบ แต่ว่าในแต่ละคาบจะไม่เหมือนกันพอดี แต่เปลี่ยนไปเรื่อยๆ
นอกจากนี้แล้วก็ยังมีฟังก์ชันเคอร์เนลอยู่อีกหลากหลายรูปแบบ ที่ยกมาในนี้เป็นแค่ส่วนหนึ่งที่ใช้ง่ายเพื่อทำความเข้าใจในเบื้องต้น
บทถัดไป >> บทที่ ๑๔