[python] วิเคราะห์ความสัมพันธ์ระหว่างตัวแปรจากค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
เขียนเมื่อ 2018/05/17 10:43
แก้ไขล่าสุด 2021/09/28 16:42
บทความนี้เขียนขึ้นเพื่อเป็นเนื้อหาคณิตศาสตร์เสริมประกอบบทเรียนเรื่องการเรียนรู้ของเครื่อง
ในนี้จะมีการแสดงสมการอธิบาย พร้อมกับโค้ดไพธอนคำนวณเป็นตัวอย่างเพื่อประกอบความเข้าใจด้วย
ในการเรียนรู้ของเครื่องนั้นเรามักจะต้องเผชิญกับตัวแปรต่างๆมากมาย ซึ่งพัวพันอยู่ในปัญหาที่เราต้องการแก้
ในระหว่างวิเคราะห์ค่าตัวแปรต่างๆนั้นสิ่งสำคัญอย่างหนึ่งที่อาจต้องพิจารณาก็คือการกระจายของค่าตัวแปรต่างๆ และความสัมพันธ์ระหว่างตัวแปรต่างๆ
เช่นถ้าตัวแปรนี้เพิ่มแล้ว อีกตัวแปรจะมีแนวโน้มเพิ่มตามหรือเปล่า หรือว่าไม่เกี่ยวข้องอะไรกันเลย นั่นคือสิ่งที่น่าจะต้องการจะรู้
สิ่งที่จะบอกว่าตัวแปรสองตัวมีความสัมพันธ์กันยังไง มีการแปรผันไปตามกันมากแค่ไหนนั้น อาจหาจากค่า
- ความแปรปรวนร่วมเกี่ยว (协方差, covariance)
- สหสัมพันธ์ (相关系数, correlation)
เมื่อคำนวณทั้ง ๒ อย่างนี้ จะช่วยให้สามารถวิเคราะห์และเข้าใจความสัมพันธ์ระหว่างตัวแปรได้
ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน
ความแปรปรวนร่วมเกี่ยวนั้นเป็นคำที่มาจากความแปรปรวน (方差, variance) แล้วก็เติมคำว่า ร่วมเกี่ยว (co) เข้าไป จึงหมายถึงว่าค่าความแปรปรวนจากการพิจารณาตัวแปรต่างๆ
ดังนั้นก่อนอื่นต้องเข้าใจก่อนว่าความหมายของความแปรปรวนในทางคณิตศาสตร์หมายถึงอะไร
ความแปรปรวนหมายถึงค่าคาดหมายของกำลังสองของความต่างจากค่าคาดหมายของตัวแปรนั้น
..(1)
โดยในที่นี้ E หมายถึงค่าคาดหมาย (期望值, expected value)
ค่าคาดหมาย ถ้าให้อธิบายง่ายๆก็คือค่าเฉลี่ยนั่นเอง เพียงแต่ว่าในกรณีที่ค่าแต่ละตัวมีการถ่วงน้ำหนักค่าความคาดหมายจะต้องคิดค่าน้ำหนักด้วย ซึ่งจะต่างไปจากค่าเฉลี่ย แต่ในที่นี้ไม่จำเป็นต้องพูดถึง ดังนั้นให้ถือว่าเป็นค่าเฉลี่ย
รากที่สองของความแปรปรวนเรียกว่าส่วนเบี่ยงเบนมาตรฐาน (标准差, standard deviation) มักเขียนแทนด้วย σ
..(2)
ตัวอย่าง สมมุติมีค่าตัวแปรชุดนึง มีค่าดังนี้
สามารถหาค่าความแปรปรวนได้ดังนี้
แต่ว่า numpy ได้เตรียมวิธีการหาค่าความแปรปรวนไว้อยู่แล้ว คือฟังก์ชัน var
การคำนวณความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
สมมุติว่ามีตัวแปรที่พิจารณาอยู่ ๒ ตัว x และ y
ความแปรปรวนร่วมเกี่ยวคำนวณได้จากค่าคาดหมายของผลคูณระหว่างความต่างจากค่าคาดหมายของตัวแปรทั้งสอง นั่นคือ
..(3)
โดยที่
..(4)
ส่วนค่าสหสัมพันธ์จะมีค่าเท่ากับความแปรปรวนร่วมเกี่ยวหารด้วยผลคูณของส่วนเบี่ยงเบนมาตรฐาน
..(5)
ยกตัวอย่าง สมมุติว่า ร้านอาหารแห่งหนึ่งต้องการเทียบปริมาณกาแฟร้อนที่ขายได้ในแต่ละวันเทียบกับอุณหภูมิสูงสุดของแต่ละวัน เมื่อวาดการกระจายออกมาได้ผลดังนี้
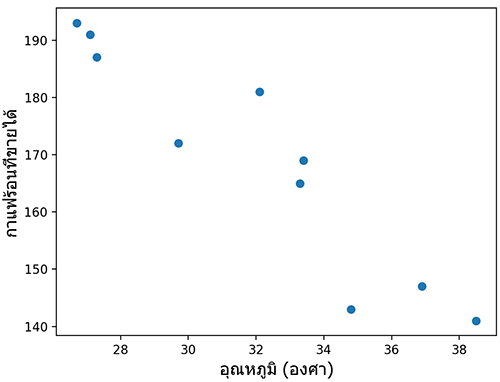
อาจเขียนโค้ดในไพธอนได้ดังนี้
สามารถหาค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ได้ด้วยสมการ (3) และ (5) ข้างต้น นำมาเขียนเป็นโค้ดได้ดังนี้
ค่าที่ได้มานี้เป็นลบ บอกแนวโน้มว่ายิ่งอุณหภูมิสูงก็ยิ่งขายกาแฟร้อนได้น้อย
การตีความค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
เพื่อให้เห็นภาพรวมชัดขึ้น ลองสร้างภาพแสดงตัวอย่างเปรียบเทียบระหว่างลักษณะการกระจายและค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ที่ได้ดูได้ดังนี้
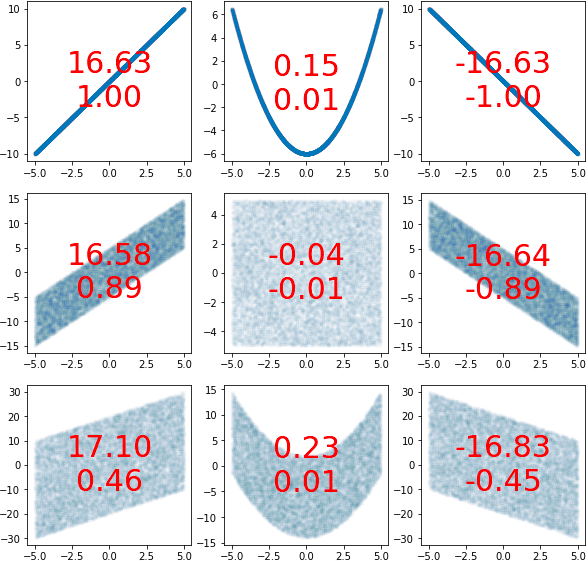
โดยเลขตัวบนคือความแปรปรวนร่วมเกี่ยว ตัวล่างคือสหสัมพันธ์
โค้ดที่ใช้สร้างภาพนี้คือ
จะเห็นว่าทั้งความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์นั้นเมื่อดูว่าค่าเป็นบวกหรือลบสามารถบอกได้คร่าวๆว่า
- หากค่าเป็นบวก จะบ่งบอกถึงว่าเมื่อ x เพิ่ม y ก็มีแนวโน้มจะเพิ่มด้วย
- หากเป็นลบ หมายถึงว่าเมื่อ x เพิ่ม y ก็มีแนวโน้มจะลด
- แต่ถ้าเป็น 0 นั่นหมายความว่าไม่ว่า x จะเพิ่มหรือลดยังไงก็ไม่อาจบอกได้ว่า y จะเพิ่มหรือว่าลด
เพียงแต่ว่า ต่อให้ค่าเป็น 0 ก็ไม่ได้หมายความว่า x หรือ y ไม่ได้มีความสัมพันธ์ใดๆกัน เพียงแต่อาจแค่เพราะความสัมพันธ์นั้นมีการกระจายในช่วงบวกและลบพอๆกันจนหักล้างกัน
เช่นในกรณี x≈y2 เป็นต้น มีช่วงนึงที่ y เพิ่มตาม x และอีกช่วง y ลดเมื่อ x เพิ่ม ทั้งสองส่วนหักล้างกันหมด
ที่จริงแถวตรงกลางตามหลักแล้วควรจะเป็น 0 ทั้งหมด แต่เนื่องจากความไม่แน่นอนในการสุ่มจึงทำให้เบี่ยงเบนไปจาก 0 เล็กน้อย
ข้อแตกต่างของความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ก็คือ สหสัมพันธ์จะมีการหารค่าความแปรปรวนที่เกิดขึ้นภายในตัวแปรเอง ทำให้ค่าที่ได้ไม่ขึ้นอยู่กับความแปรปรวนภายใน และค่าจะอยู่ระหว่าง -1 ถึง 1 เสมอ
โดยถ้าสหสัมพันธ์เป็น 1 แสดงว่า x ∝ y โดยสมบูรณ์ ถ้าเป็น -1 หมายถึง x ∝ -y
ดังนั้นถ้าต้องการจะบอกว่าตัวแปรสองตัวมีการแปรเปลี่ยนไปตามกันมากแค่ไหนเมื่อเทียบกับความแปรปรวนในตัวแปรนั้นๆเอง ดูค่าสหสัมพันธ์จะบอกได้ชัดกว่า
ในขณะที่ถ้าต้องการรู้ทั้งความสัมพันธ์ระหว่างตัวแปรพร้อมกับความแปรปรวนภายในด้วย ต้องดูค่าความแปรปรวนร่วมเกี่ยว
การแสดงความสัมพันธ์ระหว่างตัวแปรในรูปเมทริกซ์
ในการอธิบายความสัมพันธ์ระหว่างตัวแปรหลายตัว ความแปรปรวนร่วมเกี่ยวอาจถูกเขียนออกมาในรูปแบบของเมทริกซ์ โดยนำตัวแปรทั้งหมดที่มีมาจับคู่กันให้หมด เรียกว่าเมทริกซ์ความแปรปรวนร่วมเกี่ยว (协方差矩阵, covariance matrix)
กรณีที่มีแค่ ๒ ตัวแปร x และ y จะได้เมทริกซ์จตุรัสขนาด 2×2 แบบนี้
..(6)
และถ้าหากมีหลายตัวแปร เช่นเป็น x1,x2,...,xn ก็จะออกมาเป็นแบบนี้ ความกว้างและความสูงของเมทริกซ์จะเท่ากับจำนวนตัวแปร
..(7)
จะเห็นได้ว่าเมทริกซ์ที่ได้จะเป็นเมทริกซ์สมมาตรเสมอ คือส่วนบนขวาและซ้ายล่างมีค่าเท่ากัน เพราะการคูณมีสมบัติการสลับที่
โดยในส่วนแนวทแยงนั้นคือส่วนที่พิจารณาความแปรปรวนร่วมเกี่ยวของตัวแปรตัวเดียวกัน ซึ่งที่ได้ออกมาก็คือค่าความแปรปรวนของตัวแปรนั้นเอง ซึ่งเป็นสิ่งที่บ่งบอกถึงขนาดของการกระจายที่เกิดจากตัวแปรนั้นๆเองโดยไม่เกี่ยวกับตัวอื่น
ส่วนสหสัมพันธ์จะเป็นแบบนี้
กรณี ๒ ตัวแปร
..(8)
กรณีหลายตัวแปร
..(9)
จะเห็นว่าค่าในแนวทแยงเป็น 1 เสมอ
ตัวอย่างการใช้งาน เช่น ร้านนึงต้องการหาความสัมพันธ์ระหว่างอุณหภูมิสูงสุดของวันกับจำนวนน้ำแข็งไสและข้าวเหนียวมะม่วงที่ขายได้
ได้
ผลที่ได้บอกให้รู้ว่าเมื่ออุณหภูมิสูงขึ้นจะขายน้ำแข็งไสได้มากขึ้นเยอะ แต่ขายข้าวเหนียวมะม่วงได้ลดลงเล็กน้อย
ในการคำนวณหากไม่ต้องการใช้ฟังก์ชันสำเร็จอยากจะเขียนคำนวณเองก็อาจเขียนได้ดังนี้
นอกจากนี้ใน numpy ยังมีฟังก์ชัน np.correlate() ซึ่งเอาไว้ใช้สหสัมพันธ์ไขว้ ไม่เหมือนกับ np.corrcoef() วัตถุประสงค์ในการใช้ก็ต่างกัน รายละเอียดอ่านได้ใน https://phyblas.hinaboshi.com/20180609
สหสัมพันธ์ในอนุกรมเวลา
เพื่อความเข้าใจมากขึ้น มีอีกตัวอย่างหนึ่งที่น่ายกมาอธิบายถึงคือ สหสัมพันธ์ของค่าอะไรบางอย่างที่เรียงกันตามลำดับเวลา
สมมุติว่ามีค่าอะไรบางอย่างที่เปลี่ยนแปลงไปตามเวลา แล้วเราอยากหาว่าค่าในเวลาหนึ่งมันเกี่ยวพันกับค่าในอีกเวลาหนึ่งยังไง
ค่าที่เรียงตามลำดับเวลาอาจมีความสัมพันธ์กันหรืออาจไม่จำเป็นต้องมีความสัมพันธ์กันเลยก็ได้
เช่น ทอยลูกเต๋า ๗ ครั้ง แล้วเอาค่าของทั้ง ๗ ครั้งมาเขียนเรียงกันเป็นกราฟ ทำแบบนี้ทั้งหมด ๒๐ รอบ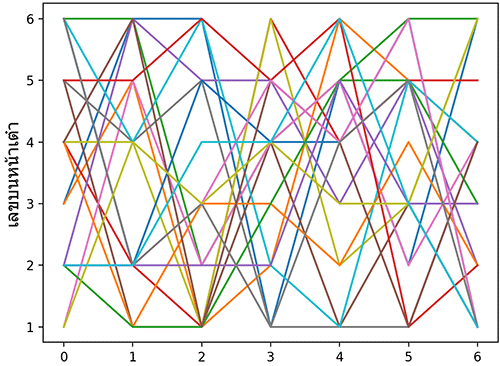
แต่ละเส้นแทนการลองทอย ๗ ครั้ง ทำแบบนี้ทั้งหมด ๒๐ รอบ
จะเห็นว่าแต่ละครั้งก็มีโอกาสได้ค่า 1-6 เท่ากัน ค่าที่ได้ไม่ได้เกี่ยวอะไรกับการโยนครั้งก่อนๆเลย
ดังนั้นเมื่อหาค่าสหสัมพันธ์ของแต่ละครั้งการทอยออกมาก็จะพบว่าค่าออกมาใกล้ 0 เต็มไปหมด ตัวแปรที่สุ่มขึ้นมาโดยเป็นอิสระจากกันจะหาสหสัมพันธ์ได้เข้าใกล้ 0
ได้
ลองนำมาแสดงในรูปแบบของช่องระบายสีน่าจะเห็นภาพชัดขึ้น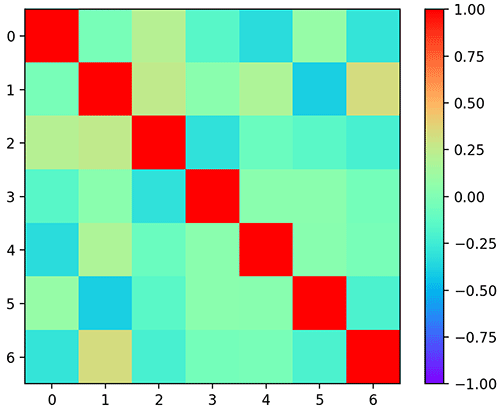
แต่หากเปลี่ยนจากค่าที่ทอยได้ในแต่ละครั้งมาเป็นแต้มสะสม เช่นครั้งแรกได้ 6 นับเป็น 6 ต่อมาได้ 5 ก็บวกเพิ่มเป็น 11 แบบนี้ละก็ แบบนี้แสดงว่าค่าของครั้งถัดๆไปจะขึ้นอยู่กับว่าครั้งก่อนทอยได้เท่าไหร่ด้วย แบบนี้สหสัมพันธ์จะไม่เป็น 0
ตัวอย่าง ลองเขียนดู สามารถทำได้ง่ายโดยใช้คำสั่ง cumsum
พอลองมาหาสหสัมพันธ์ดูใหม่
ก็จะพบว่าได้แบบนี้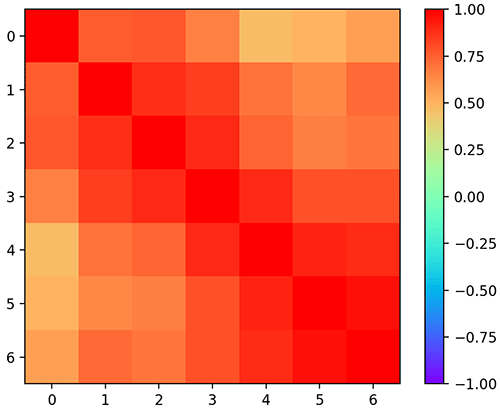
คราวนี้จะเห็นว่าส่วนที่อยู่ใกล้แนวทแยงจะมีค่าเข้าใกล้ 1 เพราะค่าของแต่ละครั้งมีความเกี่ยวเนื่องจากครั้งที่แล้วมานั่นเอง แต่จุดที่ยิ่งห่างออกไปก็มีความเกี่ยวพันน้อยลงจึงมีค่าน้อยลงเรื่อยๆ
ในธรรมชาติทั่วไปค่าหนึ่งๆในอนุกรมเวลามักจะมีความเกี่ยวพันกับค่าก่อนหน้าหรือข้างหลังไม่มากก็น้อย สหสัมพันธ์จะเป็นตัวบอกได้ว่าค่านั้นจะมีความเกี่ยวพันกันแค่ไหนอย่างไร
ทั้งหมดนี้เป็นคำอธิบายและตัวอย่างคร่าวๆของการใช้ความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
ทั้งสองอย่างนี้ถูกใช้อย่างกว้างขวางในสาขาการเรียนรู้ของเครื่อง ดังนั้นในบทความอื่นๆหลังจากนี้ก็จะมีกล่าวถึงอีก เช่น ใช้สร้างค่าสุ่มด้วยการแจกแจงแบบปกติหลายตัวแปร https://phyblas.hinaboshi.com/20180525
ในนี้จะมีการแสดงสมการอธิบาย พร้อมกับโค้ดไพธอนคำนวณเป็นตัวอย่างเพื่อประกอบความเข้าใจด้วย
ในการเรียนรู้ของเครื่องนั้นเรามักจะต้องเผชิญกับตัวแปรต่างๆมากมาย ซึ่งพัวพันอยู่ในปัญหาที่เราต้องการแก้
ในระหว่างวิเคราะห์ค่าตัวแปรต่างๆนั้นสิ่งสำคัญอย่างหนึ่งที่อาจต้องพิจารณาก็คือการกระจายของค่าตัวแปรต่างๆ และความสัมพันธ์ระหว่างตัวแปรต่างๆ
เช่นถ้าตัวแปรนี้เพิ่มแล้ว อีกตัวแปรจะมีแนวโน้มเพิ่มตามหรือเปล่า หรือว่าไม่เกี่ยวข้องอะไรกันเลย นั่นคือสิ่งที่น่าจะต้องการจะรู้
สิ่งที่จะบอกว่าตัวแปรสองตัวมีความสัมพันธ์กันยังไง มีการแปรผันไปตามกันมากแค่ไหนนั้น อาจหาจากค่า
- ความแปรปรวนร่วมเกี่ยว (协方差, covariance)
- สหสัมพันธ์ (相关系数, correlation)
เมื่อคำนวณทั้ง ๒ อย่างนี้ จะช่วยให้สามารถวิเคราะห์และเข้าใจความสัมพันธ์ระหว่างตัวแปรได้
ความแปรปรวนและส่วนเบี่ยงเบนมาตรฐาน
ความแปรปรวนร่วมเกี่ยวนั้นเป็นคำที่มาจากความแปรปรวน (方差, variance) แล้วก็เติมคำว่า ร่วมเกี่ยว (co) เข้าไป จึงหมายถึงว่าค่าความแปรปรวนจากการพิจารณาตัวแปรต่างๆ
ดังนั้นก่อนอื่นต้องเข้าใจก่อนว่าความหมายของความแปรปรวนในทางคณิตศาสตร์หมายถึงอะไร
ความแปรปรวนหมายถึงค่าคาดหมายของกำลังสองของความต่างจากค่าคาดหมายของตัวแปรนั้น
..(1)
โดยในที่นี้ E หมายถึงค่าคาดหมาย (期望值, expected value)
ค่าคาดหมาย ถ้าให้อธิบายง่ายๆก็คือค่าเฉลี่ยนั่นเอง เพียงแต่ว่าในกรณีที่ค่าแต่ละตัวมีการถ่วงน้ำหนักค่าความคาดหมายจะต้องคิดค่าน้ำหนักด้วย ซึ่งจะต่างไปจากค่าเฉลี่ย แต่ในที่นี้ไม่จำเป็นต้องพูดถึง ดังนั้นให้ถือว่าเป็นค่าเฉลี่ย
รากที่สองของความแปรปรวนเรียกว่าส่วนเบี่ยงเบนมาตรฐาน (标准差, standard deviation) มักเขียนแทนด้วย σ
..(2)
ตัวอย่าง สมมุติมีค่าตัวแปรชุดนึง มีค่าดังนี้
import numpy as np
x = np.array([4.4,1.4,8.7,9.2,4.3,6.0,4.2,9.4])สามารถหาค่าความแปรปรวนได้ดังนี้
m = x.mean() # หรือ np.mean(x)
var = ((m-x)**2).mean() # หรือ np.mean((m-x)**2)
print(var) # ได้ 7.365แต่ว่า numpy ได้เตรียมวิธีการหาค่าความแปรปรวนไว้อยู่แล้ว คือฟังก์ชัน var
var = x.var() # หรือ np.var(x)การคำนวณความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
สมมุติว่ามีตัวแปรที่พิจารณาอยู่ ๒ ตัว x และ y
ความแปรปรวนร่วมเกี่ยวคำนวณได้จากค่าคาดหมายของผลคูณระหว่างความต่างจากค่าคาดหมายของตัวแปรทั้งสอง นั่นคือ
..(3)
โดยที่
..(4)
ส่วนค่าสหสัมพันธ์จะมีค่าเท่ากับความแปรปรวนร่วมเกี่ยวหารด้วยผลคูณของส่วนเบี่ยงเบนมาตรฐาน
..(5)
ยกตัวอย่าง สมมุติว่า ร้านอาหารแห่งหนึ่งต้องการเทียบปริมาณกาแฟร้อนที่ขายได้ในแต่ละวันเทียบกับอุณหภูมิสูงสุดของแต่ละวัน เมื่อวาดการกระจายออกมาได้ผลดังนี้

อาจเขียนโค้ดในไพธอนได้ดังนี้
import matplotlib.pyplot as plt
# อุณหภูมิ
x = np.array([36.9,32.1,29.7,26.7,33.4,27.1,33.3,34.8,27.3,38.5])
# จำนวนกาแฟร้อนที่ขายได้
y = np.array([147,181,172,193,169,191,165,143,187,141])
plt.xlabel(u'อุณหภูมิ (องศา)',family='Tahoma',size=14)
plt.ylabel(u'กาแฟร้อนที่ขายได้',family='Tahoma',size=14)
plt.scatter(x,y)
plt.show()สามารถหาค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ได้ด้วยสมการ (3) และ (5) ข้างต้น นำมาเขียนเป็นโค้ดได้ดังนี้
mu = x.mean() # μ
nu = y.mean() # ν
# ความแปรปรวนร่วมเกี่ยว
cov = ((x-mu)*(y-nu)).mean()
print(cov) # ได้ -69.31199999999998
var_x = ((x-mu)**2).mean()
var_y = ((y-nu)**2).mean()
# สหสัมพันธ์
cor = cov/np.sqrt(var_x*var_y) # หรือ cov/x.std()/y.std()
print(cor) # ได้ -0.9347400061127582ค่าที่ได้มานี้เป็นลบ บอกแนวโน้มว่ายิ่งอุณหภูมิสูงก็ยิ่งขายกาแฟร้อนได้น้อย
การตีความค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
เพื่อให้เห็นภาพรวมชัดขึ้น ลองสร้างภาพแสดงตัวอย่างเปรียบเทียบระหว่างลักษณะการกระจายและค่าความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ที่ได้ดูได้ดังนี้

โดยเลขตัวบนคือความแปรปรวนร่วมเกี่ยว ตัวล่างคือสหสัมพันธ์
โค้ดที่ใช้สร้างภาพนี้คือ
def coco(x,y,i):
mu = x.mean()
nu = y.mean()
cov = ((x-mu)*(y-nu)).mean()
var_x = ((x-mu)**2).mean()
var_y = ((y-nu)**2).mean()
cor = cov/np.sqrt(var_x*var_y)
plt.subplot(3,3,i)
plt.text(0,0,'%.2f\n%.2f'%(cov,cor),size=30,ha='center',va='center',color='r')
plt.scatter(x,y,marker='.',alpha=0.01)
n = 20000
x = np.random.uniform(-5,5,n)
plt.figure(figsize=[10,10])
coco(x,x*2,1)
coco(x,x**2/2-6,2)
coco(x,-x*2,3)
coco(x,x*2+np.random.uniform(-5,5,n),4)
coco(x,np.random.uniform(-5,5,n),5)
coco(x,-x*2+np.random.uniform(-5,5,n),6)
coco(x,x*2+np.random.uniform(-20,20,n),7)
coco(x,x**2/2-6+np.random.uniform(-8,8,n),8)
coco(x,-x*2+np.random.uniform(-20,20,n),9)
plt.show()จะเห็นว่าทั้งความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์นั้นเมื่อดูว่าค่าเป็นบวกหรือลบสามารถบอกได้คร่าวๆว่า
- หากค่าเป็นบวก จะบ่งบอกถึงว่าเมื่อ x เพิ่ม y ก็มีแนวโน้มจะเพิ่มด้วย
- หากเป็นลบ หมายถึงว่าเมื่อ x เพิ่ม y ก็มีแนวโน้มจะลด
- แต่ถ้าเป็น 0 นั่นหมายความว่าไม่ว่า x จะเพิ่มหรือลดยังไงก็ไม่อาจบอกได้ว่า y จะเพิ่มหรือว่าลด
เพียงแต่ว่า ต่อให้ค่าเป็น 0 ก็ไม่ได้หมายความว่า x หรือ y ไม่ได้มีความสัมพันธ์ใดๆกัน เพียงแต่อาจแค่เพราะความสัมพันธ์นั้นมีการกระจายในช่วงบวกและลบพอๆกันจนหักล้างกัน
เช่นในกรณี x≈y2 เป็นต้น มีช่วงนึงที่ y เพิ่มตาม x และอีกช่วง y ลดเมื่อ x เพิ่ม ทั้งสองส่วนหักล้างกันหมด
ที่จริงแถวตรงกลางตามหลักแล้วควรจะเป็น 0 ทั้งหมด แต่เนื่องจากความไม่แน่นอนในการสุ่มจึงทำให้เบี่ยงเบนไปจาก 0 เล็กน้อย
ข้อแตกต่างของความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์ก็คือ สหสัมพันธ์จะมีการหารค่าความแปรปรวนที่เกิดขึ้นภายในตัวแปรเอง ทำให้ค่าที่ได้ไม่ขึ้นอยู่กับความแปรปรวนภายใน และค่าจะอยู่ระหว่าง -1 ถึง 1 เสมอ
โดยถ้าสหสัมพันธ์เป็น 1 แสดงว่า x ∝ y โดยสมบูรณ์ ถ้าเป็น -1 หมายถึง x ∝ -y
ดังนั้นถ้าต้องการจะบอกว่าตัวแปรสองตัวมีการแปรเปลี่ยนไปตามกันมากแค่ไหนเมื่อเทียบกับความแปรปรวนในตัวแปรนั้นๆเอง ดูค่าสหสัมพันธ์จะบอกได้ชัดกว่า
ในขณะที่ถ้าต้องการรู้ทั้งความสัมพันธ์ระหว่างตัวแปรพร้อมกับความแปรปรวนภายในด้วย ต้องดูค่าความแปรปรวนร่วมเกี่ยว
การแสดงความสัมพันธ์ระหว่างตัวแปรในรูปเมทริกซ์
ในการอธิบายความสัมพันธ์ระหว่างตัวแปรหลายตัว ความแปรปรวนร่วมเกี่ยวอาจถูกเขียนออกมาในรูปแบบของเมทริกซ์ โดยนำตัวแปรทั้งหมดที่มีมาจับคู่กันให้หมด เรียกว่าเมทริกซ์ความแปรปรวนร่วมเกี่ยว (协方差矩阵, covariance matrix)
กรณีที่มีแค่ ๒ ตัวแปร x และ y จะได้เมทริกซ์จตุรัสขนาด 2×2 แบบนี้
..(6)
และถ้าหากมีหลายตัวแปร เช่นเป็น x1,x2,...,xn ก็จะออกมาเป็นแบบนี้ ความกว้างและความสูงของเมทริกซ์จะเท่ากับจำนวนตัวแปร
..(7)
จะเห็นได้ว่าเมทริกซ์ที่ได้จะเป็นเมทริกซ์สมมาตรเสมอ คือส่วนบนขวาและซ้ายล่างมีค่าเท่ากัน เพราะการคูณมีสมบัติการสลับที่
โดยในส่วนแนวทแยงนั้นคือส่วนที่พิจารณาความแปรปรวนร่วมเกี่ยวของตัวแปรตัวเดียวกัน ซึ่งที่ได้ออกมาก็คือค่าความแปรปรวนของตัวแปรนั้นเอง ซึ่งเป็นสิ่งที่บ่งบอกถึงขนาดของการกระจายที่เกิดจากตัวแปรนั้นๆเองโดยไม่เกี่ยวกับตัวอื่น
ส่วนสหสัมพันธ์จะเป็นแบบนี้
กรณี ๒ ตัวแปร
..(8)
กรณีหลายตัวแปร
..(9)
จะเห็นว่าค่าในแนวทแยงเป็น 1 เสมอ
ตัวอย่างการใช้งาน เช่น ร้านนึงต้องการหาความสัมพันธ์ระหว่างอุณหภูมิสูงสุดของวันกับจำนวนน้ำแข็งไสและข้าวเหนียวมะม่วงที่ขายได้
x1 = [38.9,35.5,39.3,36.5,32.9,31.2,27.7,36.8,28.0,26.7] # อุณหภูมิ
x2 = [309,274,324,282,255,289,223,296,271,254] # น้ำแข็งไส
x3 = [192,174,178,226,236,160,217,213,188,219] # ข้าวเหนียวมะม่วง
plt.scatter(x1,x2)
plt.scatter(x1,x3)
plt.xlabel(u'อุณหภูมิ (องศา)',family='Tahoma',size=14)
plt.legend([u'น้ำแข็งไส',u'ข้าวเหนียวมะม่วง'],prop={'family':'Tahoma','size':14})
plt.show()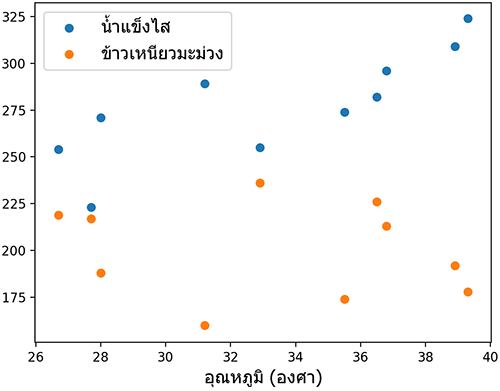
** "น้ำแข็งไส" ใช้ไม้มลาย ระวัง คนเขียนผิดกันเยอะ
ใน numpy ได้เตรียมฟังก์ชันสำหรับสร้างเมทริกซ์ความแปรปรวนร่วมเกี่ยวและเมทริกซ์สหสัมพันธ์ไว้แล้ว
cov = np.cov([x1,x2,x3])
cor = np.corrcoef([x1,x2,x3])
print(cov)
print(cor)ได้
[[ 22.47166667 111.81666667 -21.42777778]
[ 111.81666667 859.12222222 -376.9 ]
[ -21.42777778 -376.9 639.78888889]]
[[ 1. 0.80475081 -0.17870683]
[ 0.80475081 1. -0.50837047]
[-0.17870683 -0.50837047 1. ]]ผลที่ได้บอกให้รู้ว่าเมื่ออุณหภูมิสูงขึ้นจะขายน้ำแข็งไสได้มากขึ้นเยอะ แต่ขายข้าวเหนียวมะม่วงได้ลดลงเล็กน้อย
ในการคำนวณหากไม่ต้องการใช้ฟังก์ชันสำเร็จอยากจะเขียนคำนวณเองก็อาจเขียนได้ดังนี้
X = np.stack([x1,x2,x3]).T
m = X-X.mean(0)
cov = np.dot(m.T,m)/len(X)
v = X.var(0)
cor = cov/np.sqrt(v[:,None]*v)นอกจากนี้ใน numpy ยังมีฟังก์ชัน np.correlate() ซึ่งเอาไว้ใช้สหสัมพันธ์ไขว้ ไม่เหมือนกับ np.corrcoef() วัตถุประสงค์ในการใช้ก็ต่างกัน รายละเอียดอ่านได้ใน https://phyblas.hinaboshi.com/20180609
สหสัมพันธ์ในอนุกรมเวลา
เพื่อความเข้าใจมากขึ้น มีอีกตัวอย่างหนึ่งที่น่ายกมาอธิบายถึงคือ สหสัมพันธ์ของค่าอะไรบางอย่างที่เรียงกันตามลำดับเวลา
สมมุติว่ามีค่าอะไรบางอย่างที่เปลี่ยนแปลงไปตามเวลา แล้วเราอยากหาว่าค่าในเวลาหนึ่งมันเกี่ยวพันกับค่าในอีกเวลาหนึ่งยังไง
ค่าที่เรียงตามลำดับเวลาอาจมีความสัมพันธ์กันหรืออาจไม่จำเป็นต้องมีความสัมพันธ์กันเลยก็ได้
เช่น ทอยลูกเต๋า ๗ ครั้ง แล้วเอาค่าของทั้ง ๗ ครั้งมาเขียนเรียงกันเป็นกราฟ ทำแบบนี้ทั้งหมด ๒๐ รอบ
z = np.random.randint(1,7,[7,20])
plt.ylabel(u'เลขบนหน้าเต๋า',family='Tahoma',size=14)
plt.plot(z)
plt.show()
แต่ละเส้นแทนการลองทอย ๗ ครั้ง ทำแบบนี้ทั้งหมด ๒๐ รอบ
จะเห็นว่าแต่ละครั้งก็มีโอกาสได้ค่า 1-6 เท่ากัน ค่าที่ได้ไม่ได้เกี่ยวอะไรกับการโยนครั้งก่อนๆเลย
ดังนั้นเมื่อหาค่าสหสัมพันธ์ของแต่ละครั้งการทอยออกมาก็จะพบว่าค่าออกมาใกล้ 0 เต็มไปหมด ตัวแปรที่สุ่มขึ้นมาโดยเป็นอิสระจากกันจะหาสหสัมพันธ์ได้เข้าใกล้ 0
cor = np.corrcoef(z)
print(cor)ได้
[[ 1. -0.02473 0.2169 -0.1549 -0.3354 0.0869 -0.2925 ]
[-0.02473 1. 0.25 0.0443 0.187 -0.397 0.3354 ]
[ 0.2169 0.25 1. -0.3066 -0.08044 -0.1418 -0.2148 ]
[-0.1549 0.0443 -0.3066 1. 0.04312 0.04385 -0.0404 ]
[-0.3354 0.187 -0.08044 0.04312 1. 0.03293 -0.03033]
[ 0.0869 -0.397 -0.1418 0.04385 0.03293 1. -0.2001 ]
[-0.2925 0.3354 -0.2148 -0.0404 -0.03033 -0.2001 1. ]]ลองนำมาแสดงในรูปแบบของช่องระบายสีน่าจะเห็นภาพชัดขึ้น
plt.imshow(cor,vmin=-1,vmax=1,cmap='rainbow')
plt.colorbar()
plt.show()
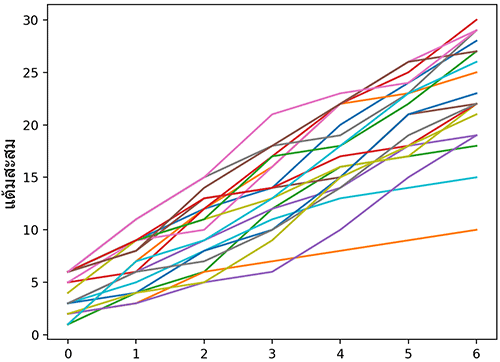
แต่หากเปลี่ยนจากค่าที่ทอยได้ในแต่ละครั้งมาเป็นแต้มสะสม เช่นครั้งแรกได้ 6 นับเป็น 6 ต่อมาได้ 5 ก็บวกเพิ่มเป็น 11 แบบนี้ละก็ แบบนี้แสดงว่าค่าของครั้งถัดๆไปจะขึ้นอยู่กับว่าครั้งก่อนทอยได้เท่าไหร่ด้วย แบบนี้สหสัมพันธ์จะไม่เป็น 0
ตัวอย่าง ลองเขียนดู สามารถทำได้ง่ายโดยใช้คำสั่ง cumsum
z = np.random.randint(1,7,[7,20]).cumsum(0)
plt.ylabel(u'แต้มสะสม',family='Tahoma',size=14)
plt.plot(z)
plt.show()
พอลองมาหาสหสัมพันธ์ดูใหม่
cor = np.corrcoef(z)
print(cor)
plt.imshow(cor,vmin=-1,vmax=1,cmap='rainbow')
plt.colorbar()
plt.show()ก็จะพบว่าได้แบบนี้
[[1. 0.7583 0.7754 0.6577 0.4717 0.5 0.5664]
[0.7583 1. 0.8813 0.843 0.6997 0.6387 0.719 ]
[0.7754 0.8813 1. 0.891 0.735 0.666 0.69 ]
[0.6577 0.843 0.891 1. 0.897 0.79 0.796 ]
[0.4717 0.6997 0.735 0.897 1. 0.912 0.8887]
[0.5 0.6387 0.666 0.79 0.912 1. 0.953 ]
[0.5664 0.719 0.69 0.796 0.8887 0.953 1. ]]
คราวนี้จะเห็นว่าส่วนที่อยู่ใกล้แนวทแยงจะมีค่าเข้าใกล้ 1 เพราะค่าของแต่ละครั้งมีความเกี่ยวเนื่องจากครั้งที่แล้วมานั่นเอง แต่จุดที่ยิ่งห่างออกไปก็มีความเกี่ยวพันน้อยลงจึงมีค่าน้อยลงเรื่อยๆ
ในธรรมชาติทั่วไปค่าหนึ่งๆในอนุกรมเวลามักจะมีความเกี่ยวพันกับค่าก่อนหน้าหรือข้างหลังไม่มากก็น้อย สหสัมพันธ์จะเป็นตัวบอกได้ว่าค่านั้นจะมีความเกี่ยวพันกันแค่ไหนอย่างไร
ทั้งหมดนี้เป็นคำอธิบายและตัวอย่างคร่าวๆของการใช้ความแปรปรวนร่วมเกี่ยวและสหสัมพันธ์
ทั้งสองอย่างนี้ถูกใช้อย่างกว้างขวางในสาขาการเรียนรู้ของเครื่อง ดังนั้นในบทความอื่นๆหลังจากนี้ก็จะมีกล่าวถึงอีก เช่น ใช้สร้างค่าสุ่มด้วยการแจกแจงแบบปกติหลายตัวแปร https://phyblas.hinaboshi.com/20180525
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คณิตศาสตร์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib