ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๔: ฟังก์ชันควรจะเป็น
เขียนเมื่อ 2020/09/02 21:58
แก้ไขล่าสุด 2021/09/28 16:42
ต่อจาก บทที่ ๑๓
ในบทนี้จะว่าด้วยเรื่องของค่าควรจะเป็นและฟังก์ชันควรจะเป็น รวมถึงการหาพารามิเตอร์ที่เหมาะสมด้วยการประมาณค่าควรจะเป็นสูงที่สุด
ความหมายของค่าควรจะเป็นและฟังก์ชันควรจะเป็น
เมื่อมีตัวแปรสุ่มบางอย่างที่เราไม่แน่ใจว่าการแจกแจงของมันเป็นอย่างไร เช่น การโยนเหรียญหัวก้อย ซึ่งเป็นการแจกแจงทวินามดังที่เขียนถึงไปในบทที่ ๕
ยกตัวอย่างง่ายๆว่า หากมีเหรียญอยู่อันหนึ่งซึ่งไม่แน่ใจว่ามีความน่าจะเป็นที่จะออกหัวอยู่เท่าใด เพื่อที่จะพิจารณาว่าความน่าจะเป็นนั้นควรจะเป็นเท่าไหร่อาจทำได้โดยการทำการทดลองโยนเหรียญแล้วดูผลที่ออกมา
ให้ เป็นผลของการโยนเหรียญ n ครั้ง ถ้าผลออกหัวให้เป็น 1 ออกก้อยให้เป็น 0
ความน่าจะเป็นที่ผลจะออกมาเป็นค่า ชุดนี้ก็คือความน่าจะเป็นร่วมของแต่ละตัว
ในกรณีโยนเหรียญ การโยนเหรียญแต่ละครั้งเป็นอิสระต่อกัน ดังนั้นจึงแยกออกเป็นในรูปผลคูณได้
ในที่นี้ ∏ แทนการเอาตัวเลขมาคูณกัน คล้ายกับที่ ∑ ใช้แสดงถึงการบวกรวมกัน
สำหรับกรณีโยนเหรียญ ถ้าเหรียญมีความน่าจะเป็นที่จะออกหัวเป็น p โยน n ครั้ง ได้หัว k ครั้ง แบบนี้ความน่าจะเป็นร่วมก็จะเป็น
ค่าความน่าจะเป็นร่วมนี้จะออกมาเป็นเท่าใดก็ขึ้นอยู่กับความน่าจะเป็น p แต่นี่เป็นค่าพารามิเตอร์ที่เราไม่รู้และต้องการหา
วิธีการคิดอย่างง่ายที่สุดก็คือ ดูว่าความน่าจะเป็นร่วมที่ได้นี้มีค่าเท่าใด ถ้ายิ่งสูงแสดงว่าค่า p นั้นน่าจะมีโอกาสทำให้เกิดผลตามที่เป็นอยู่นั้นมาก ดังนั้นหาค่า p ที่ทำให้คิดค่าความน่าจะเป็นร่วมรวมนั้นได้สูงที่สุด
ในที่นี้ความน่าจะเป็นร่วม จะเรียกว่าเป็น ฟังก์ชันควรจะเป็น (似然函数, likelihood function) คือเป็นฟังก์ชันที่จะคำนวณค่าควรจะเป็น (似然, likelihood) ซึ่งเป็นค่าที่มีความสำคัญเพราะเอาไว้บอกถึงความเหมาะสมถูกต้องของการแจกแจงที่กำลังพิจารณาอยู่
* อนึ่ง ในที่นี้แยกแยะคำว่า "ความน่าจะเป็น" (probability) กับ "ค่าควรจะเป็น" (likelihood) เป็นคนละความหมายชัดเจน แม้แปลเป็นไทยแล้วจะดูคล้ายกันแต่ถือเป็นคนละคำ ระวังจะสับสน
ที่จริงค่าควรจะเป็นก็คือความน่าจะเป็นชนิดหนึ่ง แต่ใช้เรียกค่าความน่าจะเป็นร่วมที่จะทำให้เกิดผลออกมาเป็นข้อมูลที่พิจารณาอยู่ ดังที่ได้กล่าวไป
การเปรียบเทียบค่าควรจะเป็น
ค่าความควรจะเป็นเป็นตัวที่จะบอกว่าผลที่ออกมานี้มีโอกาสเกิดขึ้นมากน้อยแค่ไหน ถ้าค่ายิ่งมากก็ยิ่งแปลว่าสมเหตุสมผล
การพิจารณาหารูปแบบการแจกแจงที่เหมาะสมโดยดูว่าการแจกแจงแบบไหนให้ค่าควรจะเป็นสูงที่สุดนั้นเรียกว่า การประมาณค่าควรจะเป็นสูงที่สุด (最大似然估计, maximum likelihood estimation)
หากรูปแบบการแจกแจงได้ถูกกำหนดไว้แน่นอนแล้ว เช่นกรณีโยนเหรียญซึ่งมีรูปแบบการแจกแจงเป็นแบบทวินาม ค่าที่สำคัญที่เป็นตัวทำให้ค่าควรจะเป็นได้ต่างกันออกไปคือค่า p ในที่นี้ถือเป็นพารามิเตอร์ที่พิจารณา
ตัวอย่างเช่น สมมุติว่าโยนเหรียญ 5 ครั้ง ได้ผลเป็น [ก้อย, หัว, ก้อย, ก้อย, หัว] ลองเขียนโปรแกรมเพื่อคำนวณค่าควรจะเป็น โดยดูกรณีที่ p=0.4 และ p=0.5 แล้วเทียบกัน
x = [0,1,0,0,1]
n = len(x) # จำนวนทั้งหมด
k = sum(x) # จำนวนที่ได้หัว
p = 0.4
llh = p**k * (1-p)**(n-k)
print(llh) # ได้ 0.03456
p = 0.5
llh = p**k * (1-p)**(n-k)
print(llh) # ได้ 0.03125จะเห็นว่าเมื่อ p = 0.4 จะได้ค่าควรจะเป็นสูงกว่า จึงสามารถมองได้ว่าเป็นคำตอบที่สมเหตุสมผลกว่า
คราวนี้ลองให้ p เป็นค่าหลายๆค่า ลองตั้งแต่ 0, 0.05, 0.1, ... , 0.95, 1 แล้ววาดกราฟเทียบผลที่ได้
import matplotlib.pyplot as plt
p = []
llh = []
for j in range(21):
p_j = 0.05*j
llh_j = p_j**k * (1-p_j)**(n-k)
p += [p_j]
llh += [llh_j]
plt.title(f'$x={x}$')
plt.xlabel('p')
plt.ylabel('ค่าควรจะเป็น',family='Tahoma')
plt.plot(p,llh,'mo-')
plt.grid(ls='--')
plt.show()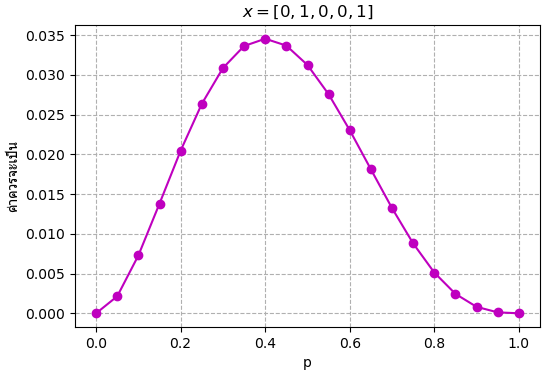
จากกราฟก็จะเห็นได้ว่าค่าควรจะเป็นสูงสุดที่ p=0.4 ดังนั้นการสรุปว่าเหรียญนี้มีความน่าจะเป็นที่จะออกหัวเป็น 0.4 จึงดูจะสมเหตุสมผลที่สุด
ในหลายกรณีสามารถหาค่าจุดสูงสุดได้โดยหาจุดที่มีอนุพันธ์เป็น 0
เช่นกรณีโยนเหรียญนี้ อาจลองคำนวณได้ดังนี้
ผลที่ออกมาก็เป็นไปตามที่ควรจะเป็น คือความน่าจะเป็น p ที่ควรจะเป็นที่สุดคือจำนวนครั้งที่ออกหัว k หารด้วยจำนวนครั้งทั้งหมด n
สมมุติว่าเหรียญออกหัว 1 ครั้งจาก 5 ครั้ง แบบนี้กราฟก็จะกลายเป็นแบบนี้
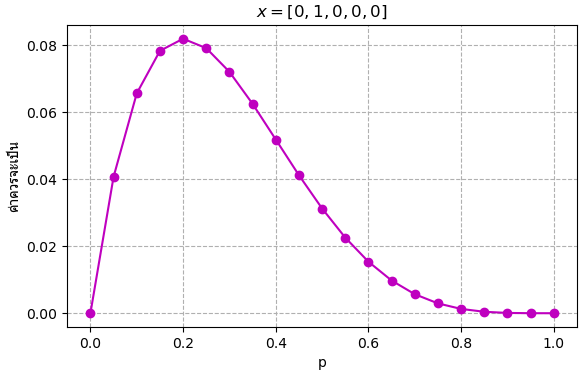
ถ้าเหรียญออกหัว 2 ครั้งจาก 10 ครั้ง จุดสูงสุดก็จะไม่ต่างจาก คืออยู่ที่ 1/5 แต่จะเห็นว่ากราฟถูกบีบแคบลง หมายความว่าความน่าจะเป็นที่จะเป็นค่าเท่านี้ยิ่งมีมากขึ้นเมื่อเทียบกับค่าอื่น
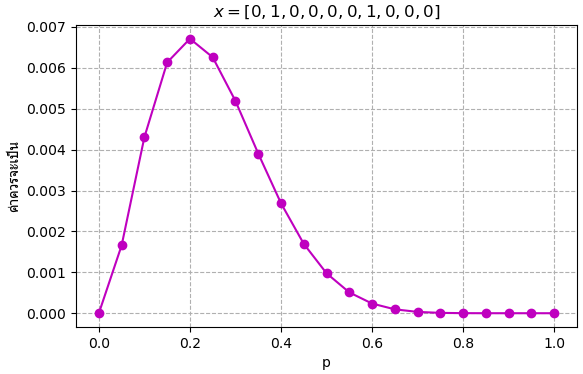
ยิ่งเพิ่มจำนวนการลอง โดยที่สัดส่วนจำนวนออกหัวก้อยยังเท่าเดิมอยู่ ก็ยิ่งจะเห็นผลชัดขึ้น เช่นถ้าออกหัว 3 ครั้งจาก 15 ครั้ง กราฟก็จะยิ่งแคบ
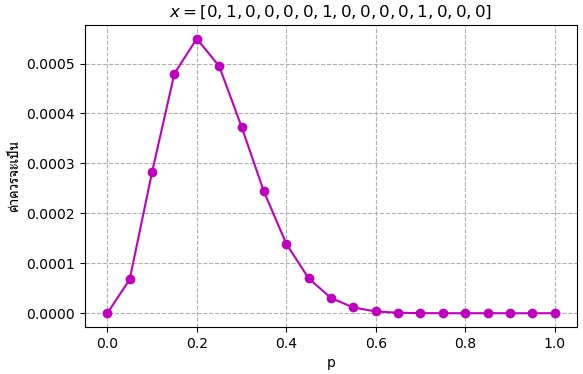
ลองยกอีกตัวอย่างหนึ่ง เช่นเล่นเกมแล้วตีมอนสเตอร์ที่มีโอกาสดร็อปไอเท็ม ต้องการจะรู้ว่าความน่าจะเป็นในการดร็อปไอเท็มเป็นเท่าไหร่ จึงลองตีมอนสเตอร์ดูสัก 10 ตัวก็พบว่าดร็อป 1 ครั้ง พอตี 100 ก็ดร็อป 10 พอตี 1000 ก็ดร็อป 100 เมื่อลองคำนวณค่าควรจะเป็นที่ p ค่าต่างๆแล้ววาดกราฟดูก็จะได้ลักษณะแบบนี้
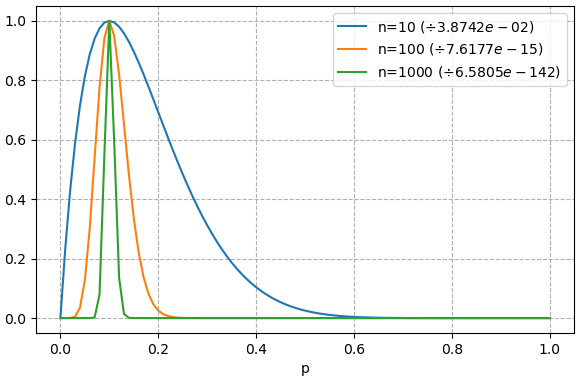
อนึ่ง ยิ่งทำจำนวนครั้งมากค่าควรจะเป็นก็ยิ่งต่ำเข้าใกล้ 0 แต่ยังไงก็เป็นค่าที่มีความแตกต่างกันชัดเจนเทียบกันได้ มีค่าสูงสุดชัดเจน ในที่นี้จึงแสดงเป็นค่าเทียบกับค่าสูงสุด (ทำให้สูงสุดเป็น 1) เพื่อให้เทียบกราฟได้
จะเห็นว่ายิ่งจำนวนครั้งมากก็ยิ่งบีบเข้ามาเป็นแท่งแคบลง การที่กราฟแคบลงแบบนี้ก็แสดงว่ายิ่งน่าจะเป็นค่านั้นแน่นอนยิ่งขึ้น ดังนั้นก็จะเห็นว่ายิ่งทดลองซ้ำมากเข้า การประมาณค่าควรจะเป็นก็ยิ่งให้ผลที่แน่นอนยิ่งขึ้น
ลอการิธึมของค่าควรจะเป็น
ค่าควรจะเป็นเกิดจากการคูณกันของเลขหลายๆตัว ซึ่งลักษณะแบบนี้บางทีก็คูณยาก อีกทั้งเนื่องจากว่าเลขแต่ละตัวที่มาคูณกันนั้นล้วนน้อยกว่า 1 ยิ่งคูณกันเข้ายิ่งเป็นเลขที่เล็กมาก แต่เวลาที่คำนวณในคอมพิวเตอร์ถ้าหากเลขต่ำเกินไปจะถูกปัดเป็น 0 ได้ จึงเป็นปัญหา
ดังนั้นในทางปฏิบัติแล้วแทนที่จะคำนวณค่าควรจะเป็นโดยตรง ก็เป็นคำนวณลอการิธึมของค่าควรจะเป็นแทน พอทำแบบนี้แล้วจากที่อยู่ในรูปของการคูณก็จะแปลงมาเป็นการบวกได้ และถึงค่าจะน้อยแค่ไหนพอใส่ลอการิธึมลงไปก็เป็นแค่ค่าติดลบ
ในที่นี้ แทนลอการิธึมของค่าควรจะเป็น
เนื่องจากค่าควรจะเป็นมีค่าอยู่ระหว่าง 0 ถึง 1 เสมอ ดังนั้น มีค่าติดลบเสมอ ยิ่งค่าติดลบน้อยก็แสดงว่าค่าควรจะเป็นมีค่าสูง
ดังนั้นเมื่อพิจารณาหาพารามิเตอร์ที่ทำให้ค่าความควรจะเป็นสูงที่สุด ก็สามารถเปลี่ยนมาพิจารณาหาค่า สูงสุดแทนได้ ความหมายไม่ต่างกันแต่คำนวณสะดวกกว่า
ลองวาดกราฟดูตัวอย่าง
import math
p = 0.4
P = []
L = []
P_j = 0
for j in range(99):
P_j += 0.01
P += [P_j]
L_j = p*math.log(P_j) + (1-p)*math.log(1-P_j)
L += [L_j]
plt.plot(P,L,'#78aa44')
plt.grid(ls='--')
plt.show()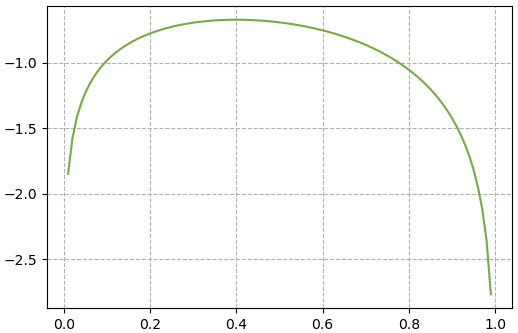
จะเห็นว่าได้กราฟที่ไม่ทำให้ค่าต่างกันมากจนเป็นเนินชันเด่นชัดเหมือนตอนก่อนใส่ลอการิธึม แต่จุดสูงสุดก็ยังคงเป็นจุดสูงสุดไม่ต่างจากเดิม
ดังนั้นจึงเป็นการสะดวกยิ่งขึ้นถ้าคำนวณเป็นค่าลอการิธึม
การกำหนดพารามิเตอร์ของการแจกแจงแบบปกติ
คราวนี้มาดูกรณีการแจกแจงแบบปกติ ซึ่งน่าจะมีโอกาสไกด้ใช้บ่อยที่สุด
ฟังก์ชันความหนาแน่นการแจกแจงความน่าจะเป็นของการแจกแจงแบบปกติเป็นดังนี้ (ยกมาจากบทที่ ๑๑)
ความน่าจะเป็นในการแจกแจงแบบปกติขึ้นกับพารามิเตอร์ 2 ตัวคือ μ และ σ ในที่นี้เราจะมาพิจารณาเพื่อหาค่าที่เหมาะสมที่สุด นั่นก็คือ μ และ σ ที่ทำให้ความน่าจะเป็นร่วมมีค่ามากที่สุด
การแจกแจงแบบปกติเป็นการแจกแจงแบบต่อเนื่อง เมื่อพิจารณาค่าควรจะเป็น แทนที่จะพิจารณาจากความน่าจะเป็นโดยตรงก็จะพิจารณาจากฟังก์ชันความหนาแน่นการแจกแจงความน่าจะเป็น ในที่นี้ขอเขียนใหม่โดยใช้อักษร ดังนี้
ความหมายในการเขียนในที่นี้เช่นเดียวกับตอนใช้ P ธรรมดา แค่เปลี่ยนเป็น แบบนี้ให้ต่างไปเล็กน้อยเพื่อแสดงถึงความหนาแน่นของความน่าจะเป็นแทนที่จะเป็นตัวค่าความน่าจะเป็น ที่จริงจะเขียนเหมือนกันก็ไม่เป็นไร บางตำราก็เขียนเป็น P เหมือนกัน ให้รู้เอาเอง แต่ในที่นี้ขอเขียนต่างเล็กน้อยให้พอรู้ว่าเป็นคนละความหมายกันแม้จะใกล้เคียงกันก็ตาม
ในที่นี้เขียน μ,σ ไว้ด้านขวาเพื่อแสดงว่าเป็นเงื่อนไขว่า μ,σ มีค่าเท่านั้น
สมมุติว่าทำการสุ่มค่าทั้งหมด n ครั้ง ได้ผลออกมาเป็น x1,x2,...,xn ค่าควรจะเป็นในกรณีของการแจกแจงแบบปกตินี้ก็คำนวณได้จากการคูณกันดังนี้
เพื่อความสะดวก ต่อไปจะพิจารณาในรูปลอการิธึมของค่าควรจะเป็น
หาอนุพันธ์เทียบกับค่า μ เพื่อจะหาจุดสูงสุด
ทำเช่นเดียวกันกับ σ
ผลที่ได้นี้จะเห็นว่า μ ก็คือค่าเฉลี่ย ส่วน σ ก็คือส่วนเบี่ยงเบนมาตรฐานนั่นเอง ซึ่งก็เป็นไปตามสมบัติของการแจกแจงแบบปกติ จะเห็นว่าสามารถพิสูจน์ได้จากการพิจารณาค่าควรจะเป็นสูงสุด
ต่อไปยกตัวอย่าง เช่นสมมุติว่ามีค่าที่ได้จากการสุ่มมา 3 ค่าเป็น [1,2,6] (เพื่อความง่ายขอยกตัวอย่างโดยใช้แค่ 3 ตัว)
ในที่นี้คำนวณได้ง่ายๆว่าค่าเฉลี่ยคือ (1+2+6)/3 = 3 และส่วนเบี่ยงเบนมาตรฐานก็จะได้เป็น 2.16
ลองเขียนโปรแกรมคำนวณค่าควรจะเป็น (ในที่นี้ขอไม่ใส่ลอการิธึม) ในกรณีค่า μ และ σ เป็นค่าต่างๆ
# ฟังก์ชันการแจกแจงความหนาแน่นความน่าจะเป็นแบบปกติ
def pakati(x,μ,σ):
return (2*math.pi)*(*-0.5)/σ*math.exp(-(x-μ)**2/(2*σ**2))
x = [1,2,6] # ตำแหน่งจุดข้อมูล
# วาดหลายๆเส้นที่ค่า σ ต่างกันไป โดยใช้ μ เป็นแกนนอน
for σ in [1.5,1.8,2.1,2.4,2.7,3]:
μ = [] # ลิสต์เก็บค่า μ
llh = [] # ลิสต์เก็บค่าความควรจะเป็นทั้งหมด
μ_j = 0.1 # ค่า μ เริ่มต้น
for j in range(100):
llh_j = 1 # ค่าความควรจะเป็น เริ่มที่ 1
# วนซ้ำเพื่อคูณเข้าไปเรื่อยๆ
for i in range(len(x)):
llh_j *= pakati(x[i],μ_j,σ)
μ += [μ_j] # เก็บค่า μ
llh += [llh_j] # เก็บค่าความควรจะเป็นที่ μ ค่านั้น
μ_j += 0.1 # เพิ่มค่า μ ไปเรื่อยๆ
plt.plot(μ,llh,label='σ=%.2f'%σ)
plt.xlabel('μ')
plt.scatter(x,[0]*len(x),c='k') # วาดจุดแสดงตำแหน่งจุดข้อมูลทั้ง 3 จุด
plt.legend()
plt.grid(ls='--')
plt.show()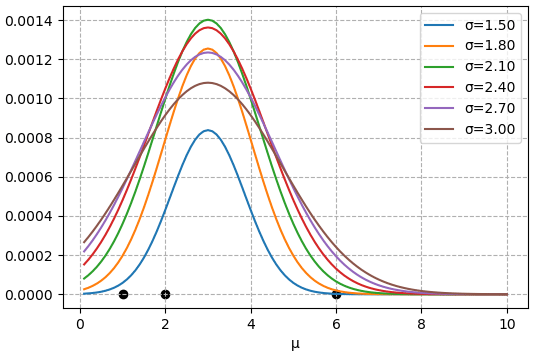
จะเห็นว่าไม่ว่า σ จะเป็นเท่าใดจุดสูงสุดก็อยู่ที่ μ=3 ซึ่งเป็นค่าเฉลี่ย แต่ค่าสูงสุดก็จะได้ต่างกันไป ขึ้นอยู่กับว่า σ เป็นเท่าใด
ลองวาดใหม่ในลักษณะเดียวกันโดยคราวนี้ให้แกนนอนเป็น σ แล้วพิจารณาเทียบที่ μ ค่าต่างๆ
for μ in [0.5,1.5,2.5,3,4,5]:
σ = []
llh = []
σ_j = 0.1
for j in range(100):
llh_j = 1
for i in range(len(x)):
llh_j *= pakati(x[i],μ,σ_j)
σ += [σ_j]
llh += [llh_j]
σ_j += 0.1
plt.plot(σ,llh,label='μ=%.1f'%μ)
plt.xlabel('σ')
plt.legend()
plt.grid(ls='--')
plt.show()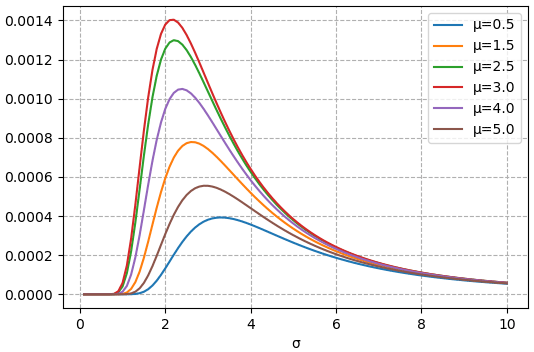
จะเห็นว่าเส้นที่มีค่าสูงที่สุดคือเส้น μ=3 และจุดสูงสุดของเส้นนี้อยู่ที่ σ=2.16 ซึ่งก็คือเท่ากับค่าส่วนเบี่ยงเบนมาตรฐาน
หากลองวาดเป็นคอนทัวร์ก็จะได้ออกมาในลักษณะนี้
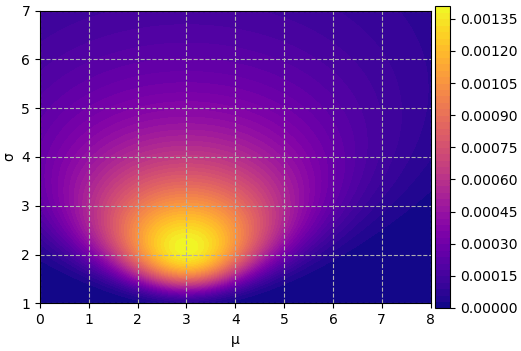
ซึ่งจะเห็นค่าสูงสุดที่ μ=3, σ=2.16
สุดท้ายเพื่อเสริมความเข้าใจให้มองเห็นภาพได้ชัดขึ้นลองดูภาพเคลื่อนไหวนี้
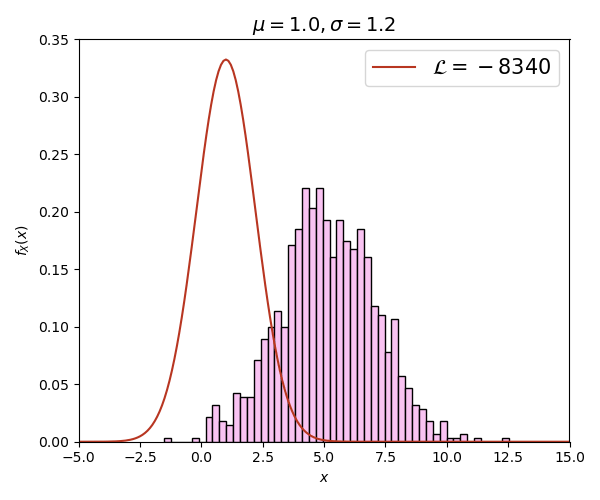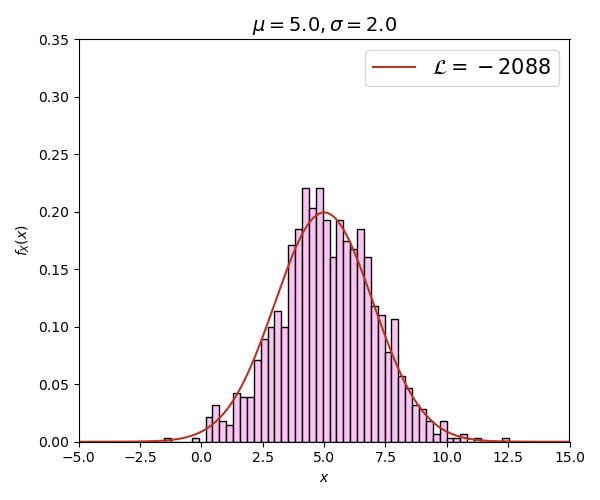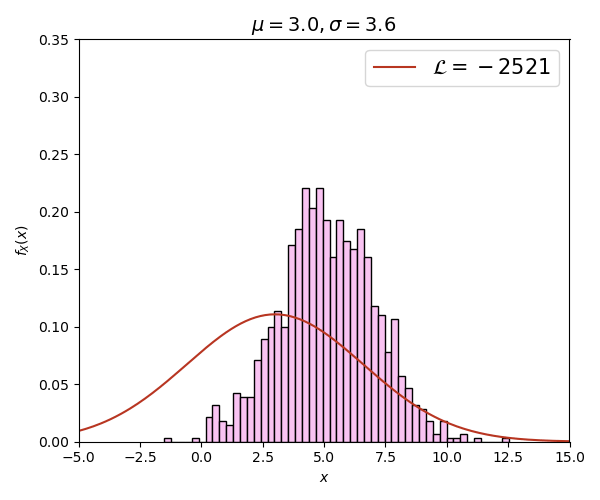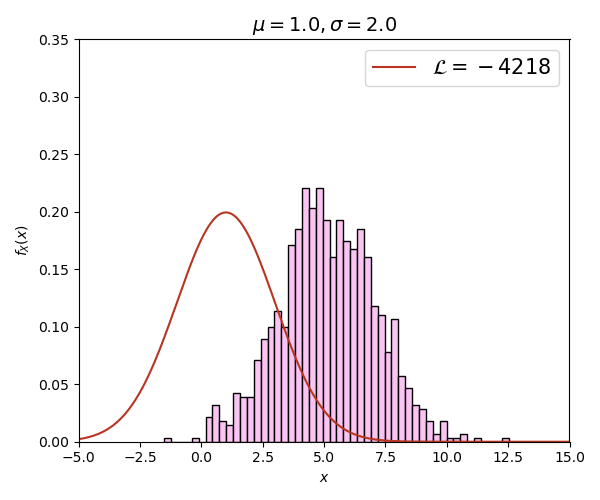
ภาพนี้สร้างจากการสุ่มข้อมูลด้วยการแจกแจงแบบปกติทั้งหมด 1000 ตัว โดยที่ μ=5, σ=2 จากนั้นลองคำนวณลอการิธึมของค่าควรจะเป็น เทียบกรณีที่ μ,σ มีค่าต่างๆกันไป
จะเห็นได้ว่าค่า เปลี่ยนไปตาม μ,σ และค่าจะสูงที่สุด (ติดลบน้อยสุด) เมื่อ μ=5, σ=2 ซึ่งตรงกับการแจกแจงจริงๆที่ใช้สุ่มสร้างข้อมูลนี้ขึ้นมา ยิ่งกราฟดูต่างไปมาก ค่า ก็ยิ่งลดลง
แนวคิดสร้างภาพและวิธีอธิบายแบบนี้ได้แรงบันดาลใจมาจากบทความ 【統計学】尤度って何?をグラフィカルに説明してみる。 ของคุณ まつ けん ในเว็บ qiita
หากใครอ่านภาษาญี่ปุ่นได้ก็ขอแนะนำให้อ่านบทความนี้ไปด้วย เพราะอธิบายเรื่องค่าควรจะเป็นได้เข้าใจง่ายเห็นภาพดีมาก
บทถัดไป >> บทที่ ๑๕