ความน่าจะเป็นเบื้องต้นสำหรับเขียนโปรแกรม บทที่ ๑๕: การแจกแจงความน่าจะเป็นภายหลังของพารามิเตอร์จากความน่าจะเป็นก่อนหน้าสังยุค
เขียนเมื่อ 2020/09/05 20:50
แก้ไขล่าสุด 2024/10/03 19:38
ต่อจาก บทที่ ๑๔
ในบทนี้จะเป็นเรื่องของการหาพารามิเตอร์ของการแจกแจงเช่นเดียวกับในบทที่แล้ว วิธีการต่อยอดจากเรื่องการหาค่าความควรจะเป็น โดยมีการนำทฤษฎีบทของเบส์มาใช้
การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงแบบต่างๆตามทฤษฎีบทของเบส์
ในบทที่ ๓ ได้เริ่มพูดถึงหลักวิธีคิดแบบเบส์และสมการของทฤษฎีบทของเบส์ไว้ว่าความน่าจะเป็นเป็นสิ่งที่เปลี่ยนแปลงไปโดยขึ้นกับข้อมูลที่มี
โดยความน่าจะเป็นก่อนจะได้ข้อมูลใหม่มาเรียกว่าเป็น ความน่าจะเป็นก่อนหน้า (先验概率, prior probability) ความน่าจะเป็นหลังจากได้ข้อมูลใหม่มาเรียกว่าเป็น ความน่าจะเป็นภายหลัง (后验概率, posterior probability)
ทฤษฎีบทของเบส์มักอธิบายด้วยสมการนี้
สำหรับในบทนี้เราจะนำทฤษฎีบทของเบส์มาใช้พิจารณาการแจกแจงความน่าจะเป็นของค่าพารามิเตอร์ที่ไม่แน่ใจค่า โดยพิจารณาจากข้อมูลที่มีอยู่ แบบนี้ A ในที่นี้จะแทนค่าพารามิเตอร์ ส่วน B จะแทนข้อมูลที่ได้มาใหม่
ดังที่ได้กล่าวถึงไปในบทที่ ๑๔ เมื่อมีเหตุการณ์บางอย่างซึ่งมีการแจกแจงความน่าจะเป็นที่ไม่แน่ใจว่ามีลักษณะเป็นอย่างไร และต้องการจะคาดการณ์โดยดูจากข้อมูลที่ทำการทดลอง สามารถทำได้โดยคำนวณฟังก์ชันควรจะเป็น (似然函数, likelihood function)
เพียงแต่ว่าวิธีนั้นเป็นแค่การตัดสินจากข้อมูลที่มีอยู่ตรงหน้าขณะนั้น โดยถือว่าทุกค่ามีความน่าจะเป็นเริ่มต้นเหมือนกันหมด
แต่ในความเป็นจริงแล้ว ถ้าเรามีข้อมูลอะไรบางอย่างมาก่อน เช่นได้มาจากการทำการทดลองก่อนหน้า ทำให้เรามีความน่าจะเป็นก่อนหน้าอยู่ เมื่อใช้หลักวิธีคิดแบบเบส์แล้วเราสามารถเอาผลก่อนหน้ามารวมกับผลที่ได้มาใหม่ เพื่อให้ได้ความน่าจะเป็นภายหลังของค่าของพารามิเตอร์นั้นที่ขึ้นกับความน่าจะเป็นก่อนหน้า
ให้ p เป็นพารามิเตอร์ของการแจกแจงที่กำลังพิจารณา และ x คือข้อมูลที่ได้มา ตามทฤษฎีบทของเบส์จะได้ว่า
โดย P(p) คือความน่าจะเป็นก่อนหน้าของค่าพารามิเตอร์ ซึ่งอาจได้จากข้อมูลที่มีมาก่อนหน้านี้ ส่วน P(x|p) คือค่าควรจะเป็นของการทดลองที่ทำใหม่
ส่วน P(x) คือความน่าจะเป็นที่จะเกิดผลดังที่เป็นอยู่นี้โดยรวมทั้งหมดโดยรวมทุกกรณีไม่ว่า p จะเป็นเท่าใด ในที่นี้เป้าหมายของเราคือหาค่าพารามิเตอร์ p แต่ค่าตัวนี้ไม่มีความเกี่ยวข้องกับพารามิเตอร์ p ดังนั้นเรามักจะไม่ต้องคำนวณค่านี้โดยตรง ค่านี้เป็นแค่ตัวหารที่เอาไว้หารแล้วทำให้การแจกแจงความน่าจะเป็นภายหลัง P(p|x) รวมแล้วเป็น 1
เมื่อพิจารณาผลคูณของความน่าจะเป็นก่อนหน้า P(p) และค่าควรจะเป็น P(x|p) ที่ได้มาใหม่ก็จะได้การแจกแจง ก็จะได้ P(p|x) คือการแจกแจงภายหลังของค่าพารามิเตอร์
เพื่อให้เห็นภาพ ต่อไปจะเริ่มยกตัวอย่างโดยใช้วิธีนี้เข้ากับการแจกแจงแบบต่างๆ
การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงทวินาม
ขอเริ่มยกตัวอย่างจากการแจกแจงที่มีรูปแบบง่ายที่สุด คือการแจกแจงทวินาม ซึ่งได้แนะนำไปในบทที่ ๕
ในที่นี้ขอเขียนแทนฟังก์ชันแจกแจงทวินามด้วย แบบนี้
โดย k คือค่าสุ่มที่จะได้จากการแจกแจง p คือพารามิเตอร์ความน่าจะเป็นที่การทดลองจะสำเร็จ ส่วน n คือจำนวนครั้งที่ทำการทดลอง
ในที่นี้จะขอแทน C(n,k) ด้วย ค่าคงที่ครอบจักรวาล (ก็คือตัว C ที่เขียนให้โค้งเว้าสวยกว่าปกติ) ซึ่งจะให้ใช้แทนค่าที่เราไม่จำเป็นต้องสนใจในการคำนวณขณะนั้น อาจเป็นเท่าใดก็ได้ขึ้นอยู่กับแต่ละสมการ
อนึ่ง ที่จริง n (จำนวนครั้งที่ทำการทดลอง) ก็เป็นพารามิเตอร์อีกตัวของการแจกแจงแบบทวินาม แต่ในที่นี้จะสนใจแค่ p โดยถือว่า n มีค่าแน่นอนอยู่แล้ว คือเรารู้ชัดว่าได้ทำการทดลองไปกี่ครั้ง (หากจะมองกรณีที่ n ไม่ทราบค่าก็จะได้การแจกแจงแบบเรขาคณิตดังที่เขียนในบทที่ ๒)
พิจารณาค่า p จากทฤษฎีบทของเบส์
เช่นเดียวกับบทที่แล้ว ในบทนี้ก็จะใช้ (ตัว P ที่เขียนให้ดูสวยขึ้น) เพื่อแทนความหนาแน่นของความน่าจะเป็นของค่าแบบต่อเนื่อง ในกรณีการแจกแจงทวินามนั้น ค่าแจกแจงคือ k เป็นค่าแบบไม่ต่อเนื่อง แต่พารามิเตอร์ p เป็นค่าใดๆตั้งแต่ 0 ถึง 1 ดังนั้นในที่นี้จึงเป็นค่าความหนาแน่นของความน่าจะเป็น ไม่ใช่ตัวค่าความน่าจะเป็น แต่ไม่ว่ากรณีไหนก็ใช้ทฤษฎีบทของเบส์ได้ แค่ต้องอย่าลืมว่าตัวไหนเป็นค่าแบบต่อเนื่องหรือค่าแบบไม่ต่อเนื่อง
P(k) เป็นค่าคงตัวที่ไม่ได้เกี่ยวกับพารามิเตอร์ p ที่พิจารณาอยู่จึงให้เข้าไปอยู่กับค่าคงที่ครอบจักรวาลด้วย
ความน่าจะเป็นก่อนหน้า เมื่อไม่มีข้อมูลใดๆมาก่อน ง่ายที่สุดคือให้เป็นค่าคงที่
ในบทที่ ๑๑ ได้เขียนถึงเรื่องการแจกแจงเบตา และได้พูดถึงว่าพารามิเตอร์ความน่าจะเป็น p ของการแจกแจงความหนาแน่นของความน่าจะเป็นมักจะมีการแจกแจงเป็นแบบเบตา
และการแจกแจงแบบคงตัวเป็นค่า 1 ในช่วง p ϵ (0,1) ก็เป็นการแจกแจงเบตาแบบหนึ่ง
ในที่นี้จะเขียนฟังก์ชันเบตาแทนด้วย แบบนี้
ในการเขียนแบบนี้ตัวที่อยู่ทางซ้ายของ | จะเขียนตัวแปรที่ต้องการแจกแจง ส่วนทางขวาของ | จะใส่พารามิเตอร์ของการแจกแจงนั้น
โดยในที่นี้ตัวแปรที่ต้องการแจกแจงคือ p ซึ่งพารามิเตอร์ความน่าจะเป็นของการแจกแจงทวินาม ส่วน α,β เป็นพารามิเตอร์ของการแจกแจงเบตา
ในการแจกแจงทวินาม p เป็นพารามิเตอร์ แต่ในการแจกแจงเบตานี้ p เป็นตัวแปรที่จะแจกแจง
ส่วน B(α,β) คือฟังก์ชันเบตา ซึ่งเป็นแค่ค่าคงที่ซึ่งไม่เกี่ยวกับค่า p สามารถที่จะไม่ต้องสนใจก็ได้ในที่นี้ ดังนั้นจะขอละไว้แล้วรวมเข้ากับส่วนของค่าคงที่ครอบจักรวาล
เมื่อ α=1,β=1 จะกลายเป็นการแจกแจงแบบคงตัวที่มีค่าเป็น 1 ตลอดตั้งแต่ p เป็น 0 ถึง 1 ในที่นี้จะใช้เป็นการแจกแจงความน่าจะเป็นก่อนหน้า
ให้ k1 และ n1 เป็นจำนวนครั้งที่สำเร็จกับจำนวนครั้งที่ทำทั้งหมดของการทดลองครั้งหนึ่ง ค่าควรจะเป็นของการทดลองนี้จะได้เป็น
ความน่าจะเป็นภายหลังของการทดลองนี้คำนวณได้จากทฤษฎีบทของเบส์ดังนี้
โดยในที่นี้ให้ความน่าจะเป็นก่อนหน้า จะได้ว่า
ในที่นี้เมื่อมองว่า p เป็นตัวแปรที่พิจารณาการแจกแจง ก็จะเห็นว่ารูปแบบการแจกแจงของ p นั้นเป็นการแจกแจงเบตา โดยที่ α=1+k1 และ β=1+n1-k1
ดังนั้นจะเห็นว่าทั้งการแจกแจงก่อนหน้าและภายหลังต่างก็เป็นฟังก์ชันเบตา
จากนั้นถ้ามีข้อมูลเพิ่มเข้ามาอีก ความน่าจะเป็นภายหลัง ก็จะกลายเป็นความน่าจะเป็นก่อนหน้าของการทดลองใหม่นี้
ค่าควรจะเป็นของการทดลองรอบนี้ก็คิดได้เช่นเดียวกับรอบแรก
แล้วก็จะผลการแจกแจงภายหลังได้เป็นฟังก์ชันเบตาเช่นเดียวกัน
ถึงตรงนี้น่าจะมองออกได้แล้วว่าถ้ามีตัวที่ 3 เข้ามาอีกก็จะได้ว่า
และถ้ามีข้อมูลใหม่เข้ามาเรื่อยๆก็จะได้ว่า
ก็จะเห็นได้ว่าสำหรับการแจกแจงทวินามนั้นเมื่อเริ่มการแจกแจงเป็นฟังก์ชันเบตาแล้วพอทำการทดลองซ้ำอีกไม่ว่าจะกี่ครั้งก็จะได้ความน่าจะเป็นภายหลังของพารามิเตอร์ p เป็นการแจกแจงเบตา
ฟังก์ชันการแจกแจงเริ่มต้นอาจจะไม่ใช่ที่ α=1,β=1 แต่ให้เป็นฟังก์ชันเบตาใดๆ โดยเริ่มต้นที่ α0,β0 ซึ่งมากกว่า 1
ในกรณีแบบนี้ เมื่อได้ข้อมูลมาใหม่ก็จะเอามารวมกับ α0,β0 เดิม
เพื่อความเข้าใจ ต่อมาเรามาลองเขียนโปรแกรมจำลองเหตุการณ์ โดยให้ p จริงๆของเหตุการณ์เป็น 0.4 แล้วทำการสุ่มไปเรื่อยๆดูว่าการแจกแจงความน่าจะเป็นของค่า p เปลี่ยนแปลงไปอย่างไร
import random,math
def beta(x,α,β):
return x**(α-1)*(1-x)**(β-1)/(math.factorial(α-1)*math.factorial(β-1)/math.factorial(α+β-1))
p = 0.4
α0 = 1 # α ตั้งต้น
β0 = 1 # β ตั้งต้น
k = 0 # จำนวนครั้งรวมที่สำเร็จ
n = 0 # จำนวนครั้งรวมที่ทำ
for i in range(21):
α = k+α0
β = n-k+β0
Pp04 = beta(0.4,α,β) # P(p=0.4)
Pp05 = beta(0.5,α,β) # P(p=0.5)
print('n=%d, α=%.d, β=%.d, P(p=0.4)=%.3f, P(p=0.5)=%.3f'%(n,α,β,Pp04,Pp05))
n += 10
for j in range(10):
# สุ่มดูว่าจะสำเร็จกี่ครั้ง
if(random.random()<p):
k += 1ผลที่ได้
n=0, α=1, β=1, P(p=0.4)=1.000, P(p=0.5)=1.000
n=10, α=5, β=7, P(p=0.4)=2.759, P(p=0.5)=2.256
n=20, α=8, β=14, P(p=0.4)=3.484, P(p=0.5)=1.553
n=30, α=13, β=19, P(p=0.4)=4.569, P(p=0.5)=2.497
n=40, α=19, β=23, P(p=0.4)=4.205, P(p=0.5)=4.228
n=50, α=21, β=31, P(p=0.4)=5.842, P(p=0.5)=2.135
n=60, α=24, β=38, P(p=0.4)=6.212, P(p=0.5)=1.237
n=70, α=27, β=45, P(p=0.4)=6.190, P(p=0.5)=0.672
n=80, α=31, β=51, P(p=0.4)=6.696, P(p=0.5)=0.594
n=90, α=33, β=59, P(p=0.4)=5.474, P(p=0.5)=0.177
n=100, α=34, β=68, P(p=0.4)=3.005, P(p=0.5)=0.023
n=110, α=38, β=74, P(p=0.4)=3.455, P(p=0.5)=0.022
n=120, α=41, β=81, P(p=0.4)=2.994, P(p=0.5)=0.010
n=130, α=47, β=85, P(p=0.4)=5.327, P(p=0.5)=0.034
n=140, α=53, β=89, P(p=0.4)=7.723, P(p=0.5)=0.091
n=150, α=58, β=94, P(p=0.4)=8.920, P(p=0.5)=0.129
n=160, α=63, β=99, P(p=0.4)=9.876, P(p=0.5)=0.175
n=170, α=68, β=104, P(p=0.4)=10.560, P(p=0.5)=0.230
n=180, α=72, β=110, P(p=0.4)=10.869, P(p=0.5)=0.193
n=190, α=74, β=118, P(p=0.4)=10.278, P(p=0.5)=0.066
n=200, α=80, β=122, P(p=0.4)=11.463, P(p=0.5)=0.136ยิ่งทดลองไปความน่าจะเป็นก็จะมากองกันอยู่ที่ p=0.4 ซึ่งเป็นค่าจริงๆของการทดลองนี้ ทำให้มั่นใจได้มากขึ้น
หากนำมาวาดกราฟทำเป็นภาพเคลื่อนไหวก็จะได้แบบนี้
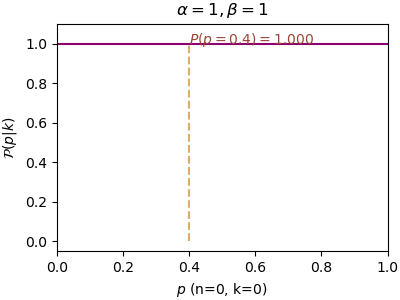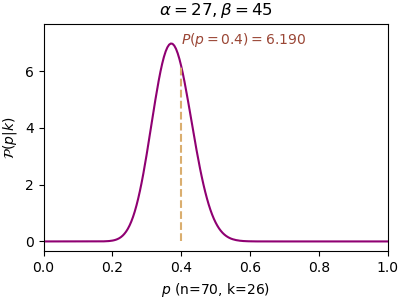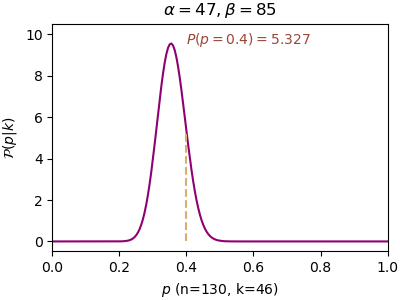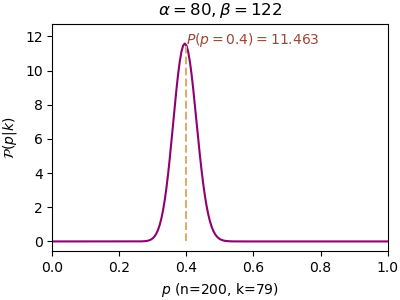
หากเปลี่ยนค่าเริ่มต้นเป็น α1=10, β1=10 ซึ่งหมายความว่าเริ่มจากการที่คิดว่าโอกาสสำเร็จมีสูงมาก จะได้กราฟออกมามีแนวโน้มไปทางขวาในตอนแรก แต่ยิ่งทดลองไปก็จะค่อยๆลู่เข้ามาจนอยู่ที่ 0.4 ได้ แม้จะช้าสักหน่อย
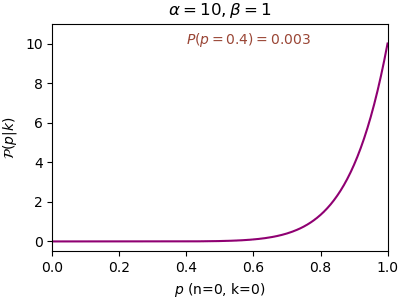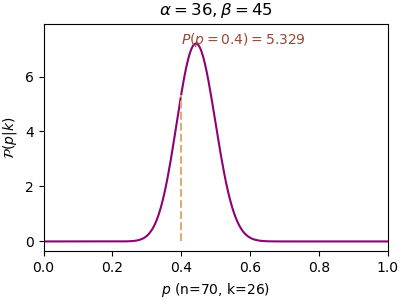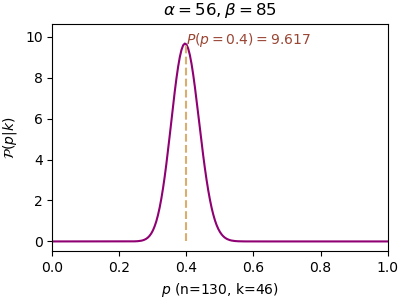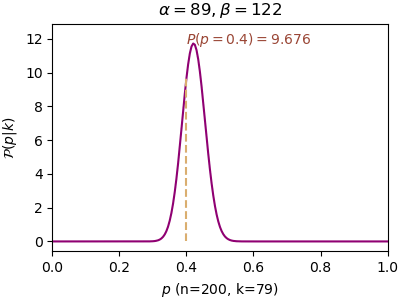
หลักการของเบส์นั้นให้ความสำคัญกับการแจกแจงเริ่มต้นซึ่งได้จากข้อมูลที่มีมาก่อนหน้า ดังนั้นการแจกแจงเริ่มต้นมีความสำคัญมาก แต่หากยิ่งทำซ้ำไปเรื่อยๆผลของการแจกแจงก่อนหน้าก็จะยิ่งจืดจางลงเรื่อยๆ
การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงแบบปกติ
ตัวอย่างต่อมาคือการแจกแจงแบบปกติ ซึ่งเป็นการแจกแจงแบบต่อเนื่องที่ใช้บ่อยที่สุด
ในที่นี้จะเขียนการแจกแจงแบบปกติด้วย แบบนี้
การแจกแจงแบบปกติมีพารามิเตอร์ 2 ตัวคือจุดกึ่งกลาง μ และความแปรปรวน σ2
ในที่นี้จะขอพิจารณาแค่การแจกแจง μ ก่อน โดยถือว่า σ2 มีค่าที่รู้แน่นอนอยู่แล้ว เมื่อใช้ทฤษฎีบทของเบส์จะเขียนได้เป็น
ในที่นี้ก็แทน เป็นค่าคงที่ครอบจักรวาลอีกเช่นเคย
การแจกแจงความน่าจะเป็นก่อนหน้านั้นเมื่อไม่มีข้อมูลอะไรมาก่อนก็อาจให้เป็นค่าคงที่แบบนี้
μ จะเป็นค่าอะไรก็ได้ตั้งแต่ -∞ ถึง ∞ ดังนั้นค่าคงที่ ในที่นี้ก็คือเป็นค่าเล็กๆเข้าใกล้ 0
หากสุ่มข้อมูลใหม่มาตัวหนึ่ง ได้เป็น x1 ค่าควรจะเป็นของการทดลองนี้คือ
การแจกแจงความน่าจะเป็นภายหลังหลังจากได้ข้อมูล x1 มาจะได้เป็น
ถ้ามองดูแล้วการแจกแจงของ μ ในที่นี้ก็เป็นการแจกแจงแบบปกติเช่นเดียวกับ x อาจเขียนได้เป็น
ในที่นี้ดูเผินๆก็เป็นการแจกแจงแบบปกติเหมือนการแจกแจงของ x แต่ต่างกันตรงที่ในนี้ตัวแปรที่แจกแจงคือ μ ไม่ใช่ x
หากมีข้อมูลใหม่ก็พิจารณาค่าควรจะเป็นของตัวใหม่เพิ่มเข้ามาอีกก็เอาความน่าจะเป็นภายหลังที่ได้นี้มาเป็นความน่าจะเป็นก่อนหน้าแล้วก็คำนวณความน่าจะเป็นภายหลังต่อไปอีก
ซึ่งข้อมูลใหม่นี้ ก็ย่อมเป็นการแจกแจงปกติเหมือนเดิม ค่าควรจะเป็นจึงเป็น
เมื่อนำผลมาต่อกัน ก็จะพบว่าผลที่ได้นั้นยังคงเขียนในรูปของการแจกแจงปกติได้อยู่
และถ้ามีข้อมูลที่ได้จากการทดลอง n ตั้ง ก็จะได้การแจกแจงความน่าจะเป็นของ μ เป็นดังนี้
ในกรณีที่มีการแจกแจงความน่าจะเป็นก่อนหน้าอยู่ตั้งแต่เริ่มต้นแล้ว และการแจกแจงนั้นเป็นการแจกแจงแบบปกติ
ในที่นี้ห้อยตัว μ ไว้หมายถึงเป็นการแจกแจงของ μ โดย μμ และ คือจุดกึ่งกลางและความแปรปรวนของการแจกแจงของค่า μ
ซึ่งจะเห็นว่าถ้า μμ = 0 และ σμ → ∞ แล้ว ดังนั้นกรณีข้างต้นที่กำหนดความน่าจะเป็นก่อนหน้าเป็นค่าคงที่นั่นก็คือเหมือนเป็นการแจกแจงแบบปกติซึ่ง μμ = 0 และ σμ → ∞ นั่นเอง
ในกรณีทั่วไปที่ความน่าจะเป็นก่อนหน้าของ μ เป็นการการแจกแจงแบบปกติอยู่แล้ว เมื่อมีข้อมูล x1 เข้ามา ความน่าจะเป็นภายหลังก็จะคำนวณได้เป็น
ในที่นี้ไม่ได้พิสูจน์ให้ดูเพราะค่อนข้างยุ่ง แต่โดยสรุปแล้วก็คือถ้าเริ่มต้นความน่าจะเป็นก่อนหน้าของ μ ด้วยการแจกแจงแบบปกติ ก็จะได้ความน่าจะเป็นภายหลังของ μ ที่เป็นการแจกแจงแบบปกติ
ถ้ามีข้อมูล n ตัวก็จะได้ว่า
ลองดูตัวอย่างการเขียนโปรแกรมจำลองการสุ่มจริง โดยให้การแจกแจงของ x เป็น μ=12 และ σ=3 โดยมีการแจกแจงความน่าจะเป็นก่อนหน้าของ μ ซึ่ง μμ=20 และ σμ=8
μ = 12 # μ จริงๆของการแจกแจง
σ = 3 # σ จริงๆของการแจกแจง
μ_μ0 = 20 # μ_μ ตั้งต้น
σ_μ0 = 8 # σ_μ ตั้งต้น
x = [] # ลิสต์เก็บค่าที่สุ่มได้ทั้งหมด
n = 0
for i in range(11):
# คำนวณ σ_μ และ μ_μ ในแต่ละรอบใหม่
σ_μ = 1/(n/σ**2+1/σ_μ0**2)**0.5
μ_μ = (sum(x)/σ**2+μ_μ0/σ_μ0**2)*σ_μ**2
print('n=%d, μ_μ=%.2f, σ_μ=%.2f'%(n,μ_μ,σ_μ))
n += 10
for j in range(10):
# ค่าใหม่สุ่มโดยแจกแจงแบบปกติโดยใช้ μ,σ จริง
x += [random.gauss(μ,σ)]ผลที่ได้
n=0, μ_μ=20.00, σ_μ=8.00
n=10, μ_μ=11.90, σ_μ=0.94
n=20, μ_μ=12.29, σ_μ=0.67
n=30, μ_μ=12.27, σ_μ=0.55
n=40, μ_μ=11.85, σ_μ=0.47
n=50, μ_μ=12.04, σ_μ=0.42
n=60, μ_μ=12.22, σ_μ=0.39
n=70, μ_μ=12.08, σ_μ=0.36
n=80, μ_μ=11.95, σ_μ=0.34
n=90, μ_μ=12.04, σ_μ=0.32
n=100, μ_μ=12.11, σ_μ=0.30ถ้าทำเป็นภาพเคลื่อนไหวก็จะออกมาแบบนี้
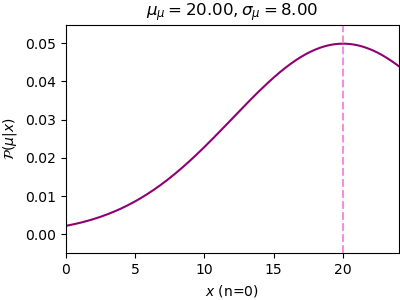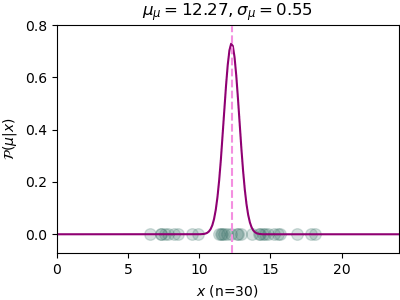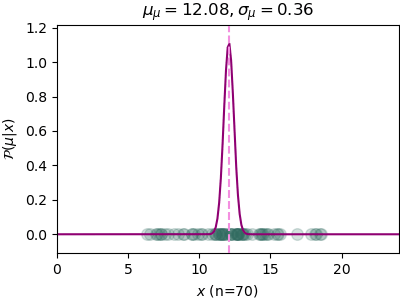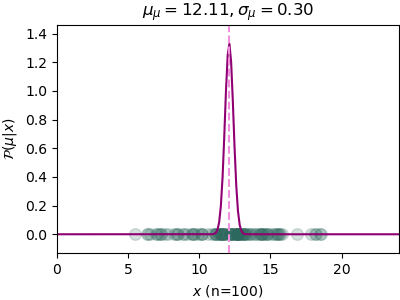
เริ่มแรกกำหนดค่าเริ่มต้นไว้ค่อนข้างห่างไกลจากความเป็นจริง แต่พอได้ข้อมูลเพิ่มขึ้นเรื่อยๆการแจกแจงความน่าจะเป็นของ μ ก็ค่อยๆลู่เข้าค่าจริงๆคือ μμ=12 ยิ่งข้อมูลมากเข้า σμ ก็ยิ่งลดลง นั่นคือค่าไปกองอยู่ที่ 12 แน่นอนมากขึ้น
การแจกแจงความน่าจะเป็นของพารามิเตอร์ของการแจกแจงแบบปกติหลายตัวแปร
ต่อมาลองพิจารณาการแจกแจงแบบปกติหลายตัวแปร (พื้นฐานเรื่องนี้ได้เขียนถึงไปใน บทที่ ๑๓)
ในที่นี้จะเขียนแทนด้วย เหมือนกับการแจกแจงแบบปกติตัวแปรเดียว เพียงแต่ค่าที่ใส่ข้างในนี้ x และ μ จะเป็นเมทริกซ์ซึ่งแสดงถึงค่าหลายมิติ และ Σ เป็นเมทริกซ์ความแปรปรวนร่วมเกี่ยว
โดย m ในที่นี้คือจำนวนมิติของ x
เช่นเดียวกับกรณีตัวแปรเดียว ความน่าจะเป็นก่อนหน้าอาจเริ่มต้นง่ายสุดจากที่เป็นค่าคงที่
แล้วการแจกแจงความน่าจะเป็นหลายหลังก็จะคำนวณได้เป็น
ผลที่ได้คล้ายกับการแจกแจงปกติตัวแปรเดียว แค่ในที่นี้ค่าแต่ละตัวเป็นเมทริกซ์
ถ้ามีข้อมูล n ตัวก็จะเป็นแบบนี้
กรณีที่มีการแจกแจงก่อนหน้าอยู่แล้วก็เช่นเดียวกัน
จะหาการแจกแจงความน่าจะเป็นภายหลังได้ดังนี้
เมื่อได้ข้อมูล n ตัว การแจกแจงความน่าจะเป็นภายหลังก็จะกลายเป็น
เนื่องจากเมทริกซ์ความแปรปรวนร่วมเกี่ยว Σ อยู่ในรูปผกผันเยอะ ถ้าเขียนใหม่ในรูปของเมทริกซ์ความเที่ยงตรง (精度矩阵, precision matrix) Λ=Σ-1 จะสะดวกในการคำนวณมากกว่า
เขียนใหม่ในรูปของ Λ เป็นดังนี้
ตัวอย่างการเขียนโปรแกรมจำลองการสุ่มข้อมูลซึ่งแจกแจงแบบปกติหลายตัวแปร โดยรู้ Σ อยู่ แล้วต้องการหาการแจกแจงความน่าจะเป็นของ
import numpy as np
μ = np.array([6,4]) # μ จริงๆของการแจกแจง
# Σ จริงๆของการแจกแจง
Σ = np.array([[3,1.5],
[1.5,2]])
Λ = np.linalg.inv(Σ)
μ_μ0 = np.array([8,2]) # μ_μ ตั้งต้น
# Σ_μ ตั้งต้น
Σ_μ0 = np.array([[8,5],
[5,8]])
Λ_μ0 = np.linalg.inv(Σ_μ0)
x = [] # ลิสต์เก็บค่าที่สุ่มได้ทั้งหมด
for n in range(26):
# คำนวณ Σ_μ และ μ_μ ในแต่ละรอบใหม่
Λ_μ = n*Λ + Λ_μ0
Σ_μ = np.linalg.inv(Λ_μ)
if(n>0):
μ_μ = np.dot(Σ_μ,np.dot(Λ,np.sum(x,0))+np.dot(Λ_μ0,μ_μ0))
else:
μ_μ = μ_μ0
print('n=%d, μ_μ=%s'%(n,μ_μ))
# สุ่มค่าใหม่
x += [np.random.multivariate_normal(μ,Σ)]ผลที่ได้
n=0, μ_μ=[8 2]
n=1, μ_μ=[7.11044694 5.53433436]
n=2, μ_μ=[7.57880249 5.64612489]
n=3, μ_μ=[7.3091354 5.35834777]
n=4, μ_μ=[6.69878049 5.10382264]
n=5, μ_μ=[7.19864577 4.78835383]
n=6, μ_μ=[7.31947603 4.73575751]
n=7, μ_μ=[7.03194893 4.43476543]
n=8, μ_μ=[7.00767772 4.41767809]
n=9, μ_μ=[6.95494665 4.70232738]
n=10, μ_μ=[6.87727517 4.54670139]
n=11, μ_μ=[6.69744769 4.47764178]
n=12, μ_μ=[6.71810945 4.4387861 ]
n=13, μ_μ=[6.54837634 4.35366301]
n=14, μ_μ=[6.46439739 4.26283085]
n=15, μ_μ=[6.47292722 4.09948288]
n=16, μ_μ=[6.46547921 4.17065036]
n=17, μ_μ=[6.395075 4.16725155]
n=18, μ_μ=[6.43901177 4.16337853]
n=19, μ_μ=[6.35743761 4.11290852]
n=20, μ_μ=[6.50691015 4.11421343]
n=21, μ_μ=[6.38746785 4.07422364]
n=22, μ_μ=[6.3124434 4.12962976]
n=23, μ_μ=[6.28712383 4.07894809]
n=24, μ_μ=[6.23349005 4.02458102]
n=25, μ_μ=[6.28488896 3.99196654]หากวาดเป็นภาพเคลื่อนไหวให้เห็นการเปลี่ยนแปลงก็จะได้ดังนี้
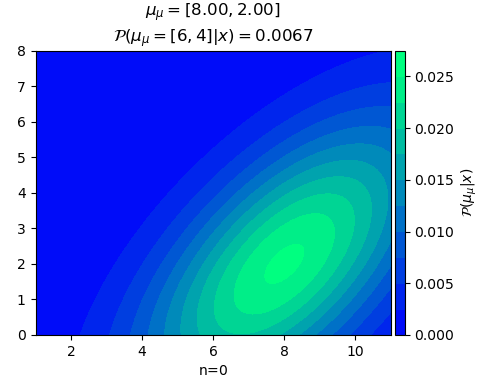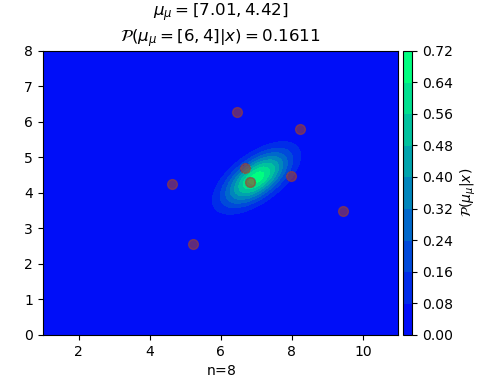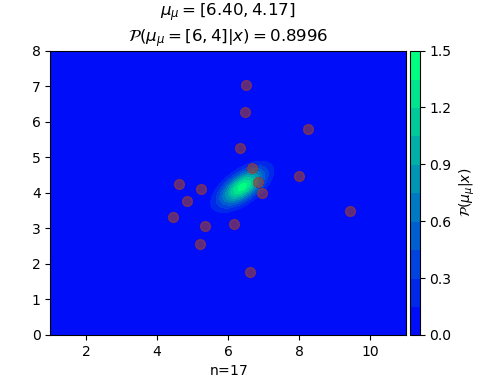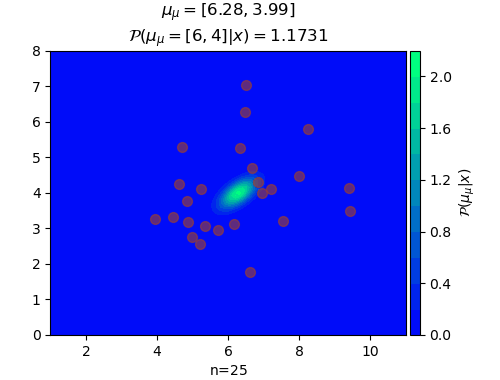
ในที่นี้สีพื้นคอนทัวร์แสดงถึงความน่าจะเป็นของค่า μ ในตำแหน่งนั้น จุดสีแดงคือจุดข้อมูลที่สุ่มขึ้นมา
ยิ่งเพิ่มจุดข้อมูลเข้าไปเรื่อยๆจุดกึ่งกลางการแจกแจงของค่า μ ก็จะเข้าใกล้ 6,4 ซึ่งเป็นค่าจริง และความแปรปรวนก็ยิ่งลดลง
ความน่าจะเป็นก่อนหน้าสังยุค
จะเห็นว่าในการแจกแจงทวินามเมื่อให้การแจกแจงความน่าจะเป็นก่อนหน้าของพารามิเตอร์ p เป็นการแจกแจงเบตา เมื่อได้ข้อมูลจากการทดลองมาเพิ่ม ความน่าจะเป็นภายหลังของ p ก็จะได้เป็นการแจกแจงแบบเบตาอีกเช่นเดิม
ลักษณะความสัมพันธ์ระหว่างการแจกแจงทวินามกับการแจกแจงเบตาในลักษณะที่กล่าวมาข้างต้นนี้เรียกว่าเป็นความน่าจะเป็นก่อนหน้าสังยุค (共轭先验, conjugate prior)
สำหรับการแจกแจงแบบปกติ เมื่อพิจารณาการแจกแจงก่อนหน้าของ μ ก็จะเห็นว่าถ้าให้ μ แจกแจงแบบปกติก็จะได้การแจกภายหลังเป็นการแจกแจงปกติเช่นกัน ดังนั้นแบบนี้ก็เรียกว่าเป็นความน่าจะเป็นก่อนหน้าสังยุคเช่นกัน เพียงแต่กรณีนี้เป็นการแจกแจงแบบปกติเหมือนกัน
นอกจากนี้แล้วยังมีความสัมพันธ์ในลักษณะนี้อยู่อีกหลายคู่ อาจสรุปได้ดังตารางนี้
| การแจกแจงของการทดลอง (ฟังก์ชันควรจะเป็น) | พารามิเตอร์ที่พิจารณา | การแจกแจงความน่าจะเป็นก่อนหน้าสังยุค |
|---|---|---|
| การแจกแจงทวินาม การแจกแจงแบร์นุลลี | p | การแจกแจงเบตา |
| การแจกแจงทวินามเชิงลบ การแจกแจงแบบเรขาคณิต | p | การแจกแจงเบตา |
| การแจกแจงอเนกนาม การแจกแจงแบบหมวดหมู่ | p | การแจกแจงดีริคเล |
| การแจกแจงปัวซง | λ | การแจกแจงแกมมา |
| การแจกแจงแบบเลขชี้กำลัง | λ | การแจกแจงแกมมา |
| การแจกแจงแบบปกติ | μ | การแจกแจงแบบปกติ |
| α (=1/σ2) | การแจกแจงแกมมา | |
| การแจกแจงแบบปกติหลายตัวแปร | μ | การแจกแจงแบบปกติหลายตัวแปร |
| Λ (=Σ-1) | การแจกแจงวิชาร์ต |
ที่อยู่ในตารางนี้มีทั้งการแจกแจงที่เคยเขียนถึงไปในบทก่อนหน้านี้แล้ว ส่วนที่ยังไม่ได้เขียนถึงก็จะกล่าวถึงในบทถัดๆไป
สำหรับการแจกแจงแบบปกตินั้นมีพารามิเตอร์ที่สำคัญ 2 ตัวคือ μ และ σ ซึ่งการแจกแจงความน่าจะเป็นก่อนหน้าสังยุคจะต่างกันออกไปขึ้นอยู่กับว่าพิจารณาตัวไหน
เพียงแต่สำหรับ σ นั้นแทนที่จะคิดการแจกแจงของ σ โดยตรงจะพิจารณาการแจกแจงของ α=1/σ2 ซึ่งเรียกว่าพารามิเตอร์ความเที่ยงตรง (精度参数, precision parameter)
เมื่อพิจารณาการแจกแจงของพารามิเตอร์ความเที่ยงตรงก็จะมีความน่าจะเป็นก่อนหน้าสังยุคเป็นการแจกแจงแกมมา
การแจกแจงแกมมายังเป็นการแจกแจงความน่าจะเป็นก่อนหน้าสังยุคของการแจกแจงปัวซงและการแจกแจงแบบเลขชี้กำลังด้วย
เรื่องของการแจกแจงแกมมาจะเขียนถึงในบทถัดไป
บทถัดไป >> บทที่ ๑๖