maya python เบื้องต้น บทที่ ๑๓: การทำภาพเคลื่อนไหวต่อเนื่องไปเรื่อยๆ
เขียนเมื่อ 2016/03/10 20:31
แก้ไขล่าสุด 2021/09/28 16:42
ในบทที่แล้วได้เข้าใจวิธีการทำภาพเคลื่อนไหวโดยใช้คีย์เฟรมไปแล้ว แต่จะเห็นว่าหลังจากที่เลยเฟรมสุดท้ายที่มีตั้งคีย์เฟรมไปแล้ว โดยทั่วไปวัตถุจะคงอยู่ในสภาพนั้นต่อไปถ้าเราไม่ได้ตั้งคีย์เฟรมต่อไปแล้ว
หากต้องการทำให้วัตถุมีการเปลี่ยนแปลงต่อไปจะต้องเซ็ตคีย์เฟรมต่อไปเรื่อยๆโดยอาจใช้ whileหรือ for เพื่อการทำซ้ำ
หรืออาจใช้วิธีการตั้งค่าเพื่อให้มีการทำต่อเนื่องไปจากคีย์เฟรมสุดท้ายที่ตั้งไว้โดยอาศัยแนวโน้มที่ต่อเนื่องมา
หากต้องการให้มันมีการเปลี่ยนแปลงค่าต่อไปโดยอาศัยแนวโน้มของคีย์เฟรมที่ตั้งไปแล้วก็สามารถทำได้โดยใช้ฟังก์ชัน setInfinity()
บทนี้ขอเริ่มอธิบายด้วยการยกตัวอย่าง
ลูกแก้วพลัง เป็นท่าไม้ตายหนึ่งของโกคู จากมังงะ (และอนิเมะ) เรื่องดรากอนบอล ในภาษาญี่ปุ่นเรียกว่าเกงกิดามะ (元気玉, genkidama) เป็นท่าที่รวบรวมพลังจากสิ่งรอบข้างมาไว้บนฝ่ามือเพื่อสร้างเป็นลูกบอลแสง ขึ้นมา ยิ่งรวบรวมพลังได้ก็ยิ่งใหญ่ขึ้น แต่ก็ต้องใช้เวลานาน
เราจะใช้มันเป็นตัวอย่างสำหรับบทนี้
เราจะให้ลูกแก้วพลังมีขนาดเริ่มต้นเป็น ๑๐ ซม. แล้วขยายขึ้นวินาทีละประมาณ ๑๐ ซม. หมายความว่าภายใน ๙ วินาทีก็จะขยายขึ้นเป็น ๑ เมตร
ดังนั้นเราต้องสร้างทรงกลมและตั้งคีย์เฟรมให้ขนาดเปลี่ยนไปตามเวลา องค์ประกอบที่กำหนดขนาดของทรงกลมก็คือ r (radius)
และเนื่องจากว่าเมื่อลูกแก้วพลังขยายขึ้นตำแหน่งของมันจะต้องอยู่สูงขึ้นเพื่อ ให้จุดล่างสุดของมันลอยอยู่บนฝ่ามือของโกคูเช่นเดิมตลอด ดังนั้นเราต้องเปลี่ยนตำแหน่งไปด้วย จึงต้องปรับ ty (translationY)
เริ่มแรกลองพิมพ์ตามนี้
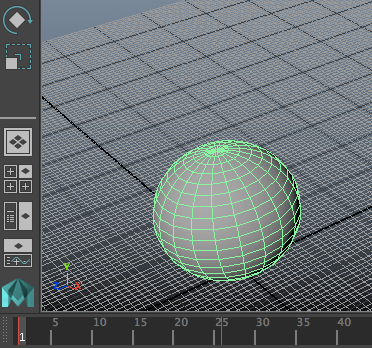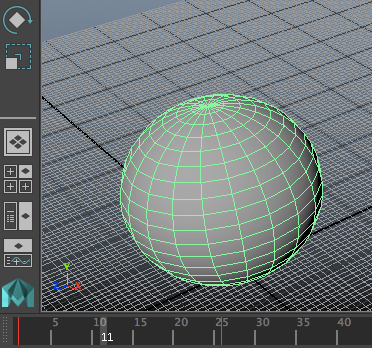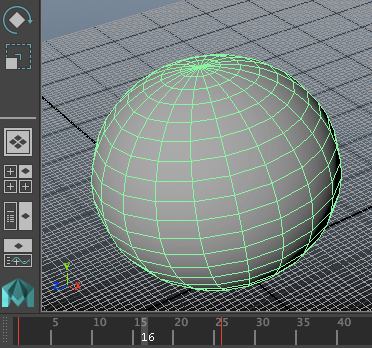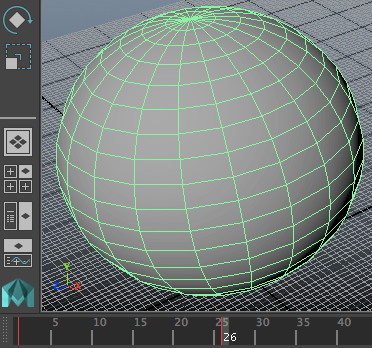
ก็จะได้ลูกบอลที่เริ่มต้นมีขนาดเป็น 10 ในเฟรมที่ 1 และขนาดเป็น 20 ในเฟรมที่ 26
อนึ่ง ต้องอย่าลืมว่าองค์ประกอบ r เป็นส่วนหนึ่งของโหนดที่กำหนดรูปร่างทรงกลม ในขณะที่โหนด ty นั้นอยู่ในโหนดหลักของวัตถุ ดังนั้นอาร์กิวเมนต์ที่ต้องใส่จึงเป็นชื่อต่างกัน ในที่นี้ใช้ลิสต์ชื่อ genkidama เป็นตัวเก็บค่าของโหนดทั้งสองซึ่งเป็นค่าคืนกลับตอนสร้างทรงกลม
จะเห็นว่าเฟรมหลังจาก 26 ไปทุกอย่างก็จะหยุดนิ่ง ไม่มีอะไรเปลี่ยนแปลงต่อ
จากตรงนี้เราต้องการให้บอลมีการขยายขนาดต่อไปเรื่อยๆโดยใช้ฟังก์ชัน setInfinity()
ฟังก์ชันนี้มีไว้กำหนดรูปแบบของค่าองค์ประกอบว่าจะเป็นยังไงหลังจากสิ้นสุดคีย์เฟรมสุดท้าย หรือก่อนเริ่มต้นคีย์
กรณี ต้องการกำหนดรูปแบบหลังคีย์เฟรมสุดท้ายให้ใช้แฟล็ก poi (postInfinite) ส่วนถ้าต้องการกำหนดรูปแบบก่อนคีย์แรกให้ใช้แฟล็ก pri (preInfinite)
โครงสร้าง เป็นดังนี้ mc.setInfinity(ชื่อวัตถุ, at=องค์ประกอบที่ต้องการตั้งค่า ,poi=รูปแบบการเปลี่ยนแปลงหลังคีย์เฟรมสุดท้าย, pri=รูปแบบการเปลี่ยนแปลงก่อนคีย์เฟรมแรก)
ในที่นี้เราจะใช้แค่ poi เพราะคีย์เฟรมแรกเราอยู่ที่คีย์เฟรมที่ 1 อยู่แล้ว ไม่จำเป็นต้องสนใจก่อนหน้านั้น
ส่วนรูปแบบนั้นมีอยู่ ๕ แบบ ประกอบไปด้วย
poi='constant' คงที่ (一定, Constant) คือไม่มีการเปลี่ยนแปลง โดยปกตินี่คือค่าตั้งต้น
poi='linear' เชิงเส้น (リニア, Linear) เปลี่ยนแปลงอย่างคงที่ต่อไปโดยไปตามความชันที่คีย์เฟรมสุดท้าย
poi='cycle' วัฏจักร (サイクル Cycle) วนซ้ำในรูปแบบเดิมไปเรื่อยๆโดยกลับมาเริ่มที่ค่าของคีย์เฟรมแรกใหม่ทุกครั้ง
poi='cycleRelative' วัฏจักรพร้อมปรับแก้ (オフセット付きサイクル, Cycle with Offset) วนซ้ำในรูปแบบเดิมไปเรื่อยๆ โดยค่าเริ่มต้นเปลี่ยนไปทุกครั้งตามความต่างของคีย์เฟรมแรกและคีย์เฟรม สุดท้าย
poi='oscillate' กลับไปกลับมา (折り返し, Oscillate) ถอยหลังกลับจากค่าที่คีย์เฟรมสุดท้ายไปยังคีย์เฟรมแรก แล้วก็วนซ้ำอีกไปเรื่อยๆ
ในที่นี้เราต้องการให้บอลขยายต่อไปเรื่อยๆโดยใช้แนวโน้มจากคีย์สุดท้าย ดังนั้นก็อาจเลือกใช้แบบ linear ดังนั้นพิมพ์ตามนี้
อย่างไรก็ตาม หากพิมพ์เพิ่มลงไปแค่นี้ก็จะพบว่าไม่มีอะไรเปลี่ยนแปลงเกิดขึ้น เพราะอะไร?
ลองมาดูที่ graph editor แล้วคลิกที่กราฟของรัศมีทรงกลมก็จะพบว่า เส้นสัมผัสทั้งด้านซ้ายและขวาชี้ไปในแนวราบ นี่เกิดจากการที่กราฟถูกปรับให้มีความชันเป็น 0 ที่จุดต้นแหละปลาย
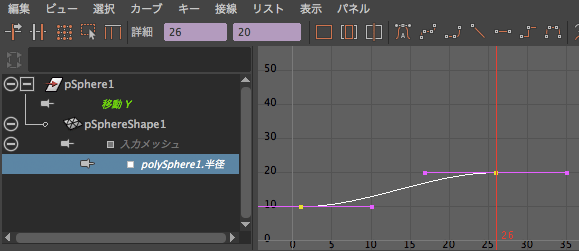
ดัง นั้นต้องทำการเปลี่ยนรูปแบบเส้นสัมผัสด้วย โดยคราวนี้จะใช้เป็นแบบ clamped ซึ่งจะคล้ายกับแบบ linear เพียงแต่เส้นสัมผัสเข้าและออกจะถูกปรับให้มีความชันเท่ากัน กราฟจึงดูต่อเนื่อง
พอพิมพ์ไปตามนี้แล้วก็จะเห็นว่ารูปร่างของกราฟเปลี่ยนไป
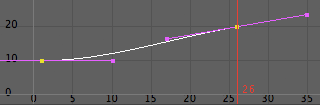
และลูกแก้วพลังก็จะขยายขนาดขึ้นไปเรื่อยๆไม่มีที่สิ้นสุด
อย่างไรก็ตามจะเห็นว่าเส้นกราฟในช่วงยังไม่ตรง ต้องปรับเส้นสัมผัสขาออกที่คีย์เฟรมแรกให้เป็น clamped ไปด้วย หรือจะเป็น linear ก็ได้
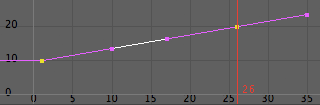
คราวนี้จะเห็นว่าลูกแก้วพลังขยายไปเรื่อยๆด้วยความเร็วคงที่
นอกจากนี้แล้วก็ยังต้องไปปรับตำแหน่งเพื่อให้ลอยขึ้นเรื่อยๆด้วย ก็สามารถปรับได้โดยทำแบบเดียวกัน
รูปแบบเส้นสัมผัสสามารถกำหนดได้ตั้งแต่ตอนที่ตั้งคีย์เฟรม ดังนั้นลบอันเก่าแล้วสร้างใหม่เลยอาจง่ายกว่า พิมพ์ตามนี้ได้เลย
ในขณะนี้หากพบว่าขอบเขตของเส้นเวลานั้นแคบเกินไปและอยากดูต่อจากนี้ไปก็สามารถ ปรับขอบเขตของเวลาให้ก้างไกลยิ่งขึ้นได้โดยใช้ฟังก์ชัน playbackOptions()
เพื่อที่จะให้เล่นได้ยาว ๑๐ วินาทีโดยเล่นรอบเดียวหยุด พิมพ์
โดยแฟล็ก min (minTime) คือขอบเขตเวลาเริ่มต้น ส่วน max (maxTime)
แฟล็ก l (loop) เป็นตัวกำหนดว่าพอเล่นไปจนสุดแล้วจะเป็นยังไงต่อ มีเลือกได้ ๓ แบบคือ
l='once' เล่นครั้งเดียวจบแล้วหยุด
l='continuous' พอเล่นจนจบก็กลับมาเริ่มที่จุดเริ่มใหม่
l='oscillate' พอเล่นจนจบก็จะเล่นย้อนถอยหลังกลับ
ตอน นี้เราได้ลูกแก้วพลังที่ใหญ่ขึ้นเรื่อยๆแล้ว แต่ว่าใหญ่ขึ้นด้วยความเร็วคงที่แบบนี้ไปเรื่อยๆมันก็ดูเหมือนขาดอะไรไป ปกติเวลาที่โกคูรวบรวมพลังลูกบอลจะค่อยๆใหญ่ขึ้นเรื่อยๆเมื่อรวบรวมพลังจาก รอบข้างมาได้ทีละนิด ดังนั้นน่าจะให้มีการขยายแล้วยุบลงนิดๆเป็นช่วงๆไปด้วยขณะที่กำลังขยาย
ซึ่งตรงนี้เราอาจทำได้ด้วยการตั้งให้เส้นสัมผัสขาเข้าของคีย์เฟรมหลังเป็นมุมติดลบนิดหน่อย
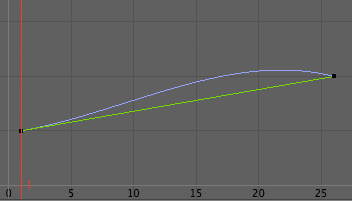
แล้วตั้ง poi เป็นแบบ cycleRelative
แบบนี้ก็จะได้บอลที่ขยายแล้วมีการยุบเล็กน้อยเป็นช่วงๆ ดูเป็นธรรมชาติมากขึ้น
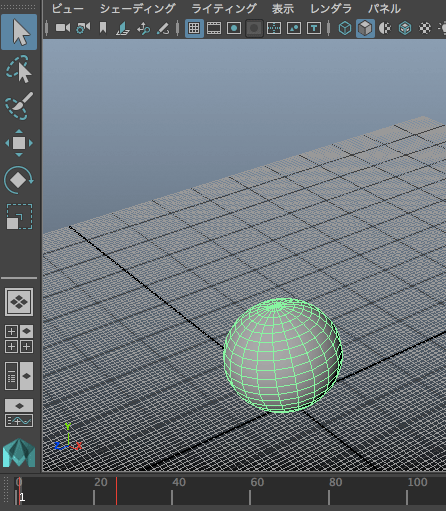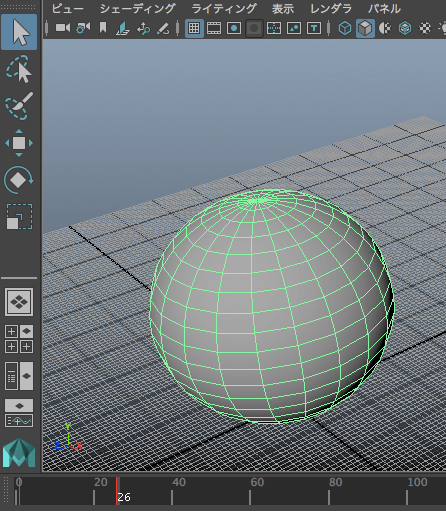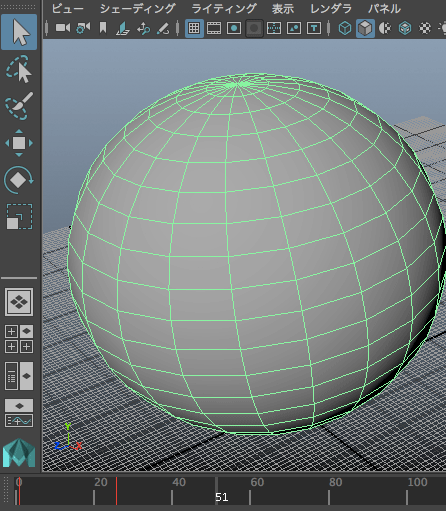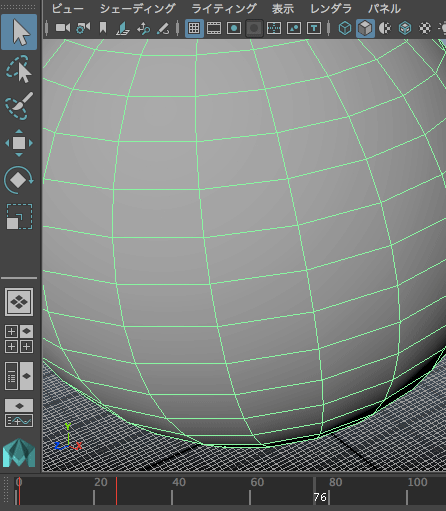
นอกจากนี้อาจลองทำให้มันมีการเคลื่อนที่ส่ายไปมาสักหน่อยด้วยอาจดูมีอะไรมากขึ้นมา ลองตั้งการเคลื่อนที่แนวแกน x โดยตั้งคีย์เฟรมสองจุดแล้วตั้ง poi เป็น oscillate
แกน z ก็ให้มีการสั่นไปด้วย แต่ให้คาบต่างกัน เริ่มที่เวลาต่างกัน และเนื่องจากคราวนี้ไม่ได้ตั้งให้เริ่มที่เฟรมที่ 1 ดังนั้นจึงควรตั้ง pri ด้วย
สรุปโค้ดทั้งหมดที่ใช้ในการสร้างลูกแก้วพลัง
อย่างไรก็ตามการใช้ setInfinity() ก็มีข้อจำกัด นั่นคือเมื่อใช้แล้วจะเป็นการทำซ้ำไปเรื่อยๆโดยที่ไม่สามารถเปลี่ยนแปลงอะไร ได้แล้ว ดังนั้นกรณีที่ทำซ้ำไปสักระยะหนึ่งแล้วต้องการมาเปลี่ยนอะไรเอาตอนหลัง วิธีนี้อาจไม่ค่อยเหมาะสมสักเท่าไหร่
เช่นลูกแก้วพลังนั้น หลังจากที่มันเติบโตจนได้ที่แล้วก็ได้เวลาเอาไปโยนเพื่อโจมตีศัตรู
ดังนั้นต่อไปจะแนะนำวิธีการทำซ้ำอีกแบบ ซึ่งสามารถปรับอะไรได้อย่างอิสระมากกว่า วิธีนั้นก็คือใช้คำสั่ง for เพื่อวนซ้ำ
ลองสร้างใหม่ตามนี้ คราวนี้ใช้ for แทน setInfinity() แล้วก็เพิ่มส่วนท้ายที่สั่งให้พุ่งไปข้างหน้า
ผลของโค้ดนี้ได้ทำเป็นคลิปเอาไว้
ขอยกอีกตัวอย่าง คือพิจารณาวัตถุที่ร่วงจากที่สูงลงไปถึงพื้นแล้วเด้งขึ้นมาใหม่
สมมุติว่าปล่อยให้วัตถุตกอย่างอิสระโดยไม่มีแรงต้านอากาศ ความสูงจะเป็นไปตามสมการ y=H-0.5*g*t**2
โดย ในที่นี้ H คือความสูงที่ปล่อย g คือค่าคงที่โน้มถ่วง มีค่าประมาณ 9.8 m/s**2 แต่ในที่นี้ขอประมาณเป็น 10 ส่วน t คือเวลาในหน่วยวินาที
จากสูตรนี้ถ้าวัตถุตกลงมาจากที่สูง ๕ เมตรก็จะถึงพื้นใน ๑ วินาที
ระหว่าง นั้นถ้าหากมีความเร็วตั้งต้นในแนวระดับด้วยวัตถุก็จะเคลื่อนที่ในแนวระดับ ด้วยความเร็วคงที่ไปพร้อมกัน x=v*t กลายเป็นการเคลื่อนที่แบบโพรเจ็กไทล์
ลองสร้างวัตถุให้ตกลงจากที่สูง ๕ เมตร โดยมีความเร็วตั้งต้นแนวระดับเป็น ๔ ใช้คำสั่ง for เพื่อตั้งคีย์เฟรมของความสูงจากพื้นทุกเฟรม
เมื่อ ดูกราฟของ ty จะพบว่าเป็นเส้นโค้งพาราโบลา และมีคีย์เฟรมขีดอยู่ทุกเฟรม ความจริงแล้วไม่จำเป็นตั้งคีย์เฟรมทุกเฟรมแบบนี้ แต่ยิ่งตั้งถี่ก็ยิ่งได้การเคลื่อนที่ที่แม่นยำยิ่งขึ้น เลือกใช้ตามความเหมาะสม
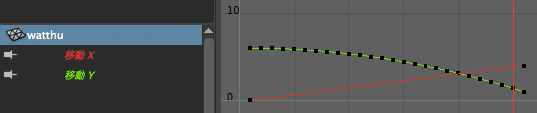
อนึ่ง ty ในที่นี้บวกครึ่งความสูงของวัตถุไปด้วย เพราะความสูงของวัตถุภายในโปรแกรมวัดจากกึ่งกลาง ไม่ใช่ใต้ก้น ดังนั้นจึง +1
จากนั้นสามารถใช้ setInfinity() เพื่อทำให้วัตถุเด้งกระดอนอย่างต่อเนื่อง
ลองลบแล้วสร้างใหม่
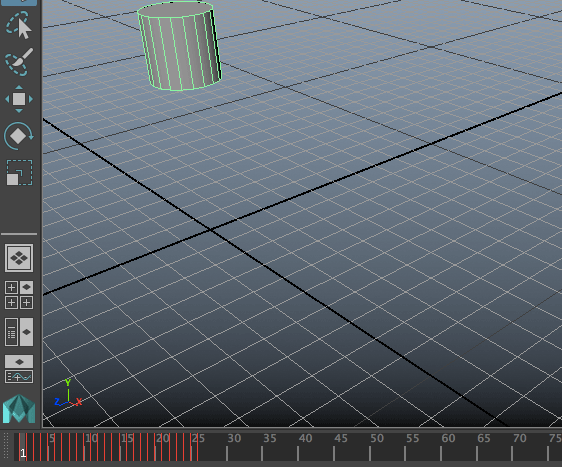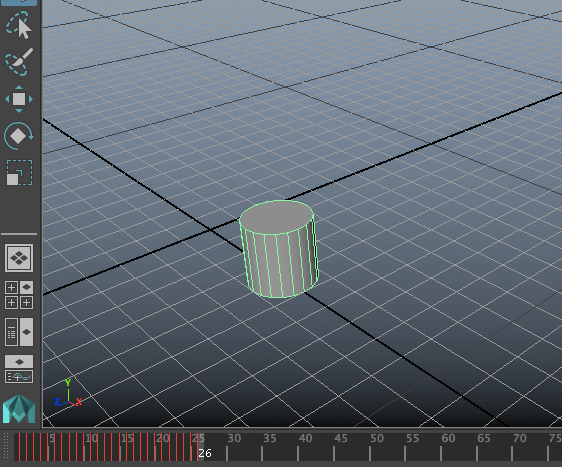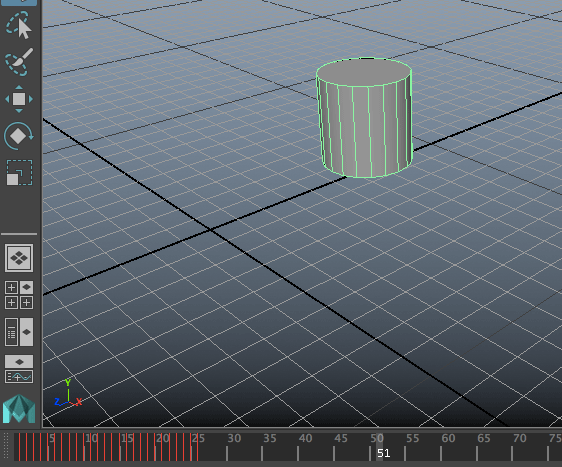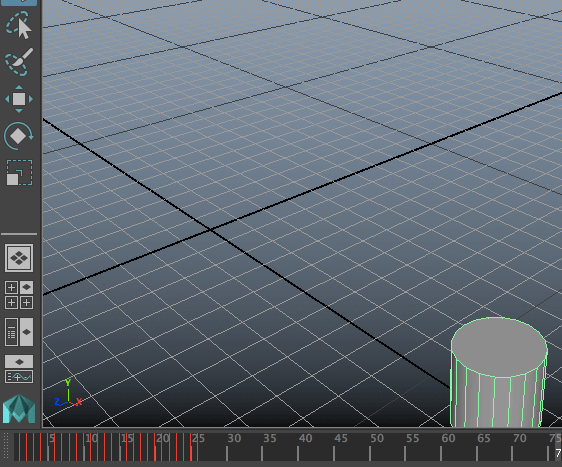
ด้วยการวนซ้ำด้วย for หรือ while บวกกับฟังก์ชัน setInfinity() ตอนนี้เราสามารถสร้างการเคลื่อนที่ในแบบต่างๆได้มากมายหลากหลายพอสมควรแล้ว
อนึ่ง ที่จริงเรื่องของการดัดกราฟนี้อาจค่อนข้างเข้าใจยาก คิดว่าคงมีหลายคนที่อ่านแล้วงงๆ หากไม่เข้าใจก็ไม่ต้องคิดมาก แค่เข้าใจเรื่องตั้งคีย์เฟรมก็เพียงพอเพราะเป็นเรื่องที่เน้นมากกว่า ส่วนกราฟนั้นจะมาปรับเมื่อต้องการเน้นรายละเอียดเท่านั้น
อ้างอิง
หากต้องการทำให้วัตถุมีการเปลี่ยนแปลงต่อไปจะต้องเซ็ตคีย์เฟรมต่อไปเรื่อยๆโดยอาจใช้ whileหรือ for เพื่อการทำซ้ำ
หรืออาจใช้วิธีการตั้งค่าเพื่อให้มีการทำต่อเนื่องไปจากคีย์เฟรมสุดท้ายที่ตั้งไว้โดยอาศัยแนวโน้มที่ต่อเนื่องมา
หากต้องการให้มันมีการเปลี่ยนแปลงค่าต่อไปโดยอาศัยแนวโน้มของคีย์เฟรมที่ตั้งไปแล้วก็สามารถทำได้โดยใช้ฟังก์ชัน setInfinity()
บทนี้ขอเริ่มอธิบายด้วยการยกตัวอย่าง
ลูกแก้วพลัง เป็นท่าไม้ตายหนึ่งของโกคู จากมังงะ (และอนิเมะ) เรื่องดรากอนบอล ในภาษาญี่ปุ่นเรียกว่าเกงกิดามะ (元気玉, genkidama) เป็นท่าที่รวบรวมพลังจากสิ่งรอบข้างมาไว้บนฝ่ามือเพื่อสร้างเป็นลูกบอลแสง ขึ้นมา ยิ่งรวบรวมพลังได้ก็ยิ่งใหญ่ขึ้น แต่ก็ต้องใช้เวลานาน
เราจะใช้มันเป็นตัวอย่างสำหรับบทนี้
เราจะให้ลูกแก้วพลังมีขนาดเริ่มต้นเป็น ๑๐ ซม. แล้วขยายขึ้นวินาทีละประมาณ ๑๐ ซม. หมายความว่าภายใน ๙ วินาทีก็จะขยายขึ้นเป็น ๑ เมตร
ดังนั้นเราต้องสร้างทรงกลมและตั้งคีย์เฟรมให้ขนาดเปลี่ยนไปตามเวลา องค์ประกอบที่กำหนดขนาดของทรงกลมก็คือ r (radius)
และเนื่องจากว่าเมื่อลูกแก้วพลังขยายขึ้นตำแหน่งของมันจะต้องอยู่สูงขึ้นเพื่อ ให้จุดล่างสุดของมันลอยอยู่บนฝ่ามือของโกคูเช่นเดิมตลอด ดังนั้นเราต้องเปลี่ยนตำแหน่งไปด้วย จึงต้องปรับ ty (translationY)
เริ่มแรกลองพิมพ์ตามนี้
genkidama = mc.polySphere(r=10)
mc.setKeyframe(genkidama[1],at='r',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',v=20,t=26)
mc.setKeyframe(genkidama[0],at='ty',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',v=20,t=26)
mc.setKeyframe(genkidama[1],at='r',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',v=20,t=26)
mc.setKeyframe(genkidama[0],at='ty',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',v=20,t=26)
ก็จะได้ลูกบอลที่เริ่มต้นมีขนาดเป็น 10 ในเฟรมที่ 1 และขนาดเป็น 20 ในเฟรมที่ 26

อนึ่ง ต้องอย่าลืมว่าองค์ประกอบ r เป็นส่วนหนึ่งของโหนดที่กำหนดรูปร่างทรงกลม ในขณะที่โหนด ty นั้นอยู่ในโหนดหลักของวัตถุ ดังนั้นอาร์กิวเมนต์ที่ต้องใส่จึงเป็นชื่อต่างกัน ในที่นี้ใช้ลิสต์ชื่อ genkidama เป็นตัวเก็บค่าของโหนดทั้งสองซึ่งเป็นค่าคืนกลับตอนสร้างทรงกลม
จะเห็นว่าเฟรมหลังจาก 26 ไปทุกอย่างก็จะหยุดนิ่ง ไม่มีอะไรเปลี่ยนแปลงต่อ
จากตรงนี้เราต้องการให้บอลมีการขยายขนาดต่อไปเรื่อยๆโดยใช้ฟังก์ชัน setInfinity()
ฟังก์ชันนี้มีไว้กำหนดรูปแบบของค่าองค์ประกอบว่าจะเป็นยังไงหลังจากสิ้นสุดคีย์เฟรมสุดท้าย หรือก่อนเริ่มต้นคีย์
กรณี ต้องการกำหนดรูปแบบหลังคีย์เฟรมสุดท้ายให้ใช้แฟล็ก poi (postInfinite) ส่วนถ้าต้องการกำหนดรูปแบบก่อนคีย์แรกให้ใช้แฟล็ก pri (preInfinite)
โครงสร้าง เป็นดังนี้ mc.setInfinity(ชื่อวัตถุ, at=องค์ประกอบที่ต้องการตั้งค่า ,poi=รูปแบบการเปลี่ยนแปลงหลังคีย์เฟรมสุดท้าย, pri=รูปแบบการเปลี่ยนแปลงก่อนคีย์เฟรมแรก)
ในที่นี้เราจะใช้แค่ poi เพราะคีย์เฟรมแรกเราอยู่ที่คีย์เฟรมที่ 1 อยู่แล้ว ไม่จำเป็นต้องสนใจก่อนหน้านั้น
ส่วนรูปแบบนั้นมีอยู่ ๕ แบบ ประกอบไปด้วย
poi='constant' คงที่ (一定, Constant) คือไม่มีการเปลี่ยนแปลง โดยปกตินี่คือค่าตั้งต้น
poi='linear' เชิงเส้น (リニア, Linear) เปลี่ยนแปลงอย่างคงที่ต่อไปโดยไปตามความชันที่คีย์เฟรมสุดท้าย
poi='cycle' วัฏจักร (サイクル Cycle) วนซ้ำในรูปแบบเดิมไปเรื่อยๆโดยกลับมาเริ่มที่ค่าของคีย์เฟรมแรกใหม่ทุกครั้ง
poi='cycleRelative' วัฏจักรพร้อมปรับแก้ (オフセット付きサイクル, Cycle with Offset) วนซ้ำในรูปแบบเดิมไปเรื่อยๆ โดยค่าเริ่มต้นเปลี่ยนไปทุกครั้งตามความต่างของคีย์เฟรมแรกและคีย์เฟรม สุดท้าย
poi='oscillate' กลับไปกลับมา (折り返し, Oscillate) ถอยหลังกลับจากค่าที่คีย์เฟรมสุดท้ายไปยังคีย์เฟรมแรก แล้วก็วนซ้ำอีกไปเรื่อยๆ
ในที่นี้เราต้องการให้บอลขยายต่อไปเรื่อยๆโดยใช้แนวโน้มจากคีย์สุดท้าย ดังนั้นก็อาจเลือกใช้แบบ linear ดังนั้นพิมพ์ตามนี้
mc.setInfinity(genkidama[1],at='r',poi='linear')
อย่างไรก็ตาม หากพิมพ์เพิ่มลงไปแค่นี้ก็จะพบว่าไม่มีอะไรเปลี่ยนแปลงเกิดขึ้น เพราะอะไร?
ลองมาดูที่ graph editor แล้วคลิกที่กราฟของรัศมีทรงกลมก็จะพบว่า เส้นสัมผัสทั้งด้านซ้ายและขวาชี้ไปในแนวราบ นี่เกิดจากการที่กราฟถูกปรับให้มีความชันเป็น 0 ที่จุดต้นแหละปลาย

ดัง นั้นต้องทำการเปลี่ยนรูปแบบเส้นสัมผัสด้วย โดยคราวนี้จะใช้เป็นแบบ clamped ซึ่งจะคล้ายกับแบบ linear เพียงแต่เส้นสัมผัสเข้าและออกจะถูกปรับให้มีความชันเท่ากัน กราฟจึงดูต่อเนื่อง
mc.keyTangent(genkidama[1],t=(26,26),at='r',ott='clamped',itt='clamped')
พอพิมพ์ไปตามนี้แล้วก็จะเห็นว่ารูปร่างของกราฟเปลี่ยนไป

และลูกแก้วพลังก็จะขยายขนาดขึ้นไปเรื่อยๆไม่มีที่สิ้นสุด
อย่างไรก็ตามจะเห็นว่าเส้นกราฟในช่วงยังไม่ตรง ต้องปรับเส้นสัมผัสขาออกที่คีย์เฟรมแรกให้เป็น clamped ไปด้วย หรือจะเป็น linear ก็ได้
mc.keyTangent(genkidama[1],t=(1,1),at='r',ott='linear')

คราวนี้จะเห็นว่าลูกแก้วพลังขยายไปเรื่อยๆด้วยความเร็วคงที่
นอกจากนี้แล้วก็ยังต้องไปปรับตำแหน่งเพื่อให้ลอยขึ้นเรื่อยๆด้วย ก็สามารถปรับได้โดยทำแบบเดียวกัน
รูปแบบเส้นสัมผัสสามารถกำหนดได้ตั้งแต่ตอนที่ตั้งคีย์เฟรม ดังนั้นลบอันเก่าแล้วสร้างใหม่เลยอาจง่ายกว่า พิมพ์ตามนี้ได้เลย
genkidama = mc.polySphere(r=10)
mc.setKeyframe(genkidama[1],at='r',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[1],at='r',poi='linear')
mc.setKeyframe(genkidama[0],at='ty',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[0],at='ty',poi='linear')
mc.setKeyframe(genkidama[1],at='r',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[1],at='r',poi='linear')
mc.setKeyframe(genkidama[0],at='ty',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[0],at='ty',poi='linear')
ในขณะนี้หากพบว่าขอบเขตของเส้นเวลานั้นแคบเกินไปและอยากดูต่อจากนี้ไปก็สามารถ ปรับขอบเขตของเวลาให้ก้างไกลยิ่งขึ้นได้โดยใช้ฟังก์ชัน playbackOptions()
เพื่อที่จะให้เล่นได้ยาว ๑๐ วินาทีโดยเล่นรอบเดียวหยุด พิมพ์
mc.playbackOptions(min=1,max=250,l='once')
โดยแฟล็ก min (minTime) คือขอบเขตเวลาเริ่มต้น ส่วน max (maxTime)
แฟล็ก l (loop) เป็นตัวกำหนดว่าพอเล่นไปจนสุดแล้วจะเป็นยังไงต่อ มีเลือกได้ ๓ แบบคือ
l='once' เล่นครั้งเดียวจบแล้วหยุด
l='continuous' พอเล่นจนจบก็กลับมาเริ่มที่จุดเริ่มใหม่
l='oscillate' พอเล่นจนจบก็จะเล่นย้อนถอยหลังกลับ
ตอน นี้เราได้ลูกแก้วพลังที่ใหญ่ขึ้นเรื่อยๆแล้ว แต่ว่าใหญ่ขึ้นด้วยความเร็วคงที่แบบนี้ไปเรื่อยๆมันก็ดูเหมือนขาดอะไรไป ปกติเวลาที่โกคูรวบรวมพลังลูกบอลจะค่อยๆใหญ่ขึ้นเรื่อยๆเมื่อรวบรวมพลังจาก รอบข้างมาได้ทีละนิด ดังนั้นน่าจะให้มีการขยายแล้วยุบลงนิดๆเป็นช่วงๆไปด้วยขณะที่กำลังขยาย
ซึ่งตรงนี้เราอาจทำได้ด้วยการตั้งให้เส้นสัมผัสขาเข้าของคีย์เฟรมหลังเป็นมุมติดลบนิดหน่อย
mc.keyTangent(genkidama[1],t=(26,26),at='r',ia=-30)

แล้วตั้ง poi เป็นแบบ cycleRelative
mc.setInfinity(genkidama[1],at='r',poi='cycleRelative')
แบบนี้ก็จะได้บอลที่ขยายแล้วมีการยุบเล็กน้อยเป็นช่วงๆ ดูเป็นธรรมชาติมากขึ้น

นอกจากนี้อาจลองทำให้มันมีการเคลื่อนที่ส่ายไปมาสักหน่อยด้วยอาจดูมีอะไรมากขึ้นมา ลองตั้งการเคลื่อนที่แนวแกน x โดยตั้งคีย์เฟรมสองจุดแล้วตั้ง poi เป็น oscillate
mc.setKeyframe(genkidama[0],at='tx',v=-10,t=1)
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11)
mc.setInfinity(genkidama[0],at='tx',poi='oscillate')
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11)
mc.setInfinity(genkidama[0],at='tx',poi='oscillate')
แกน z ก็ให้มีการสั่นไปด้วย แต่ให้คาบต่างกัน เริ่มที่เวลาต่างกัน และเนื่องจากคราวนี้ไม่ได้ตั้งให้เริ่มที่เฟรมที่ 1 ดังนั้นจึงควรตั้ง pri ด้วย
mc.setKeyframe(genkidama[0],at='tz',v=-10,t=6)
mc.setKeyframe(genkidama[0],at='tz',v=10,t=14)
mc.setInfinity(genkidama[0],at='tz',pri='oscillate',poi='oscillate')
mc.setKeyframe(genkidama[0],at='tz',v=10,t=14)
mc.setInfinity(genkidama[0],at='tz',pri='oscillate',poi='oscillate')

สรุปโค้ดทั้งหมดที่ใช้ในการสร้างลูกแก้วพลัง
genkidama = mc.polySphere(r=10)
mc.setKeyframe(genkidama[1],at='r',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[1],at='r',poi='cycleRelative')
mc.keyTangent(genkidama[1],t=(26,26),at='r',ia=-30)
mc.setKeyframe(genkidama[0],at='ty',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[0],at='ty',poi='linear')
mc.setKeyframe(genkidama[0],at='tx',v=-10,t=1)
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11)
mc.setInfinity(genkidama[0],at='tx',poi='oscillate')
mc.setKeyframe(genkidama[0],at='tz',v=-10,t=6)
mc.setKeyframe(genkidama[0],at='tz',v=10,t=14)
mc.setInfinity(genkidama[0],at='tz',pri='oscillate',poi='oscillate')
mc.setKeyframe(genkidama[1],at='r',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[1],at='r',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[1],at='r',poi='cycleRelative')
mc.keyTangent(genkidama[1],t=(26,26),at='r',ia=-30)
mc.setKeyframe(genkidama[0],at='ty',ott='linear',v=10,t=1)
mc.setKeyframe(genkidama[0],at='ty',itt='clamped',ott='clamped',v=20,t=26)
mc.setInfinity(genkidama[0],at='ty',poi='linear')
mc.setKeyframe(genkidama[0],at='tx',v=-10,t=1)
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11)
mc.setInfinity(genkidama[0],at='tx',poi='oscillate')
mc.setKeyframe(genkidama[0],at='tz',v=-10,t=6)
mc.setKeyframe(genkidama[0],at='tz',v=10,t=14)
mc.setInfinity(genkidama[0],at='tz',pri='oscillate',poi='oscillate')
อย่างไรก็ตามการใช้ setInfinity() ก็มีข้อจำกัด นั่นคือเมื่อใช้แล้วจะเป็นการทำซ้ำไปเรื่อยๆโดยที่ไม่สามารถเปลี่ยนแปลงอะไร ได้แล้ว ดังนั้นกรณีที่ทำซ้ำไปสักระยะหนึ่งแล้วต้องการมาเปลี่ยนอะไรเอาตอนหลัง วิธีนี้อาจไม่ค่อยเหมาะสมสักเท่าไหร่
เช่นลูกแก้วพลังนั้น หลังจากที่มันเติบโตจนได้ที่แล้วก็ได้เวลาเอาไปโยนเพื่อโจมตีศัตรู
ดังนั้นต่อไปจะแนะนำวิธีการทำซ้ำอีกแบบ ซึ่งสามารถปรับอะไรได้อย่างอิสระมากกว่า วิธีนั้นก็คือใช้คำสั่ง for เพื่อวนซ้ำ
ลองสร้างใหม่ตามนี้ คราวนี้ใช้ for แทน setInfinity() แล้วก็เพิ่มส่วนท้ายที่สั่งให้พุ่งไปข้างหน้า
genkidama = mc.polySphere(r=10)
for i in range(11):
t=1+25*i
mc.setKeyframe(genkidama[1],at='r',v=10+10*i,t=t)
mc.keyTangent(genkidama[1],t=(t,t),at='r',ia=-30)
mc.setKeyframe(genkidama[0],at='ty',v=10+10*i,t=t)
for i in range(13):
mc.setKeyframe(genkidama[0],at='tx',v=-10,t=1+i*20)
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11+i*20)
for i in range(16):
mc.setKeyframe(genkidama[0],at='tz',v=-10,t=6+i*16)
mc.setKeyframe(genkidama[0],at='tz',v=10,t=i*16-2)
mc.setKeyframe(genkidama[0],at='tx',v=1000,t=301)
mc.playbackOptions(min=1,max=300,l='once')
for i in range(11):
t=1+25*i
mc.setKeyframe(genkidama[1],at='r',v=10+10*i,t=t)
mc.keyTangent(genkidama[1],t=(t,t),at='r',ia=-30)
mc.setKeyframe(genkidama[0],at='ty',v=10+10*i,t=t)
for i in range(13):
mc.setKeyframe(genkidama[0],at='tx',v=-10,t=1+i*20)
mc.setKeyframe(genkidama[0],at='tx',v=10,t=11+i*20)
for i in range(16):
mc.setKeyframe(genkidama[0],at='tz',v=-10,t=6+i*16)
mc.setKeyframe(genkidama[0],at='tz',v=10,t=i*16-2)
mc.setKeyframe(genkidama[0],at='tx',v=1000,t=301)
mc.playbackOptions(min=1,max=300,l='once')
ผลของโค้ดนี้ได้ทำเป็นคลิปเอาไว้
ขอยกอีกตัวอย่าง คือพิจารณาวัตถุที่ร่วงจากที่สูงลงไปถึงพื้นแล้วเด้งขึ้นมาใหม่
สมมุติว่าปล่อยให้วัตถุตกอย่างอิสระโดยไม่มีแรงต้านอากาศ ความสูงจะเป็นไปตามสมการ y=H-0.5*g*t**2
โดย ในที่นี้ H คือความสูงที่ปล่อย g คือค่าคงที่โน้มถ่วง มีค่าประมาณ 9.8 m/s**2 แต่ในที่นี้ขอประมาณเป็น 10 ส่วน t คือเวลาในหน่วยวินาที
จากสูตรนี้ถ้าวัตถุตกลงมาจากที่สูง ๕ เมตรก็จะถึงพื้นใน ๑ วินาที
ระหว่าง นั้นถ้าหากมีความเร็วตั้งต้นในแนวระดับด้วยวัตถุก็จะเคลื่อนที่ในแนวระดับ ด้วยความเร็วคงที่ไปพร้อมกัน x=v*t กลายเป็นการเคลื่อนที่แบบโพรเจ็กไทล์
ลองสร้างวัตถุให้ตกลงจากที่สูง ๕ เมตร โดยมีความเร็วตั้งต้นแนวระดับเป็น ๔ ใช้คำสั่ง for เพื่อตั้งคีย์เฟรมของความสูงจากพื้นทุกเฟรม
mc.polyCylinder(r=1,h=2,n='watthu')
for k in range(1,27):
t=(k-1.)/25
mc.setKeyframe('watthu',at='ty',v=6-5*t**2,t=k)
mc.setKeyframe('watthu',at='tx',v=0,t=1,ott='linear')
mc.setKeyframe('watthu',at='tx',v=4,t=26,itt='linear')
for k in range(1,27):
t=(k-1.)/25
mc.setKeyframe('watthu',at='ty',v=6-5*t**2,t=k)
mc.setKeyframe('watthu',at='tx',v=0,t=1,ott='linear')
mc.setKeyframe('watthu',at='tx',v=4,t=26,itt='linear')
เมื่อ ดูกราฟของ ty จะพบว่าเป็นเส้นโค้งพาราโบลา และมีคีย์เฟรมขีดอยู่ทุกเฟรม ความจริงแล้วไม่จำเป็นตั้งคีย์เฟรมทุกเฟรมแบบนี้ แต่ยิ่งตั้งถี่ก็ยิ่งได้การเคลื่อนที่ที่แม่นยำยิ่งขึ้น เลือกใช้ตามความเหมาะสม

อนึ่ง ty ในที่นี้บวกครึ่งความสูงของวัตถุไปด้วย เพราะความสูงของวัตถุภายในโปรแกรมวัดจากกึ่งกลาง ไม่ใช่ใต้ก้น ดังนั้นจึง +1
จากนั้นสามารถใช้ setInfinity() เพื่อทำให้วัตถุเด้งกระดอนอย่างต่อเนื่อง
ลองลบแล้วสร้างใหม่
mc.polyCylinder(r=1,h=2,n='watthu')
for k in range(1,27):
t=(k-1.)/25
mc.setKeyframe('watthu',at='ty',v=6-5*t**2,t=k)
mc.setKeyframe('watthu',at='tx',v=0,t=1,ott='linear')
mc.setKeyframe('watthu',at='tx',v=4,t=26,itt='clamped',ott='clamped')
mc.setInfinity('watthu',at='tx',poi='linear')
mc.setInfinity('watthu',at='ty',poi='oscillate')
for k in range(1,27):
t=(k-1.)/25
mc.setKeyframe('watthu',at='ty',v=6-5*t**2,t=k)
mc.setKeyframe('watthu',at='tx',v=0,t=1,ott='linear')
mc.setKeyframe('watthu',at='tx',v=4,t=26,itt='clamped',ott='clamped')
mc.setInfinity('watthu',at='tx',poi='linear')
mc.setInfinity('watthu',at='ty',poi='oscillate')

ด้วยการวนซ้ำด้วย for หรือ while บวกกับฟังก์ชัน setInfinity() ตอนนี้เราสามารถสร้างการเคลื่อนที่ในแบบต่างๆได้มากมายหลากหลายพอสมควรแล้ว
อนึ่ง ที่จริงเรื่องของการดัดกราฟนี้อาจค่อนข้างเข้าใจยาก คิดว่าคงมีหลายคนที่อ่านแล้วงงๆ หากไม่เข้าใจก็ไม่ต้องคิดมาก แค่เข้าใจเรื่องตั้งคีย์เฟรมก็เพียงพอเพราะเป็นเรื่องที่เน้นมากกว่า ส่วนกราฟนั้นจะมาปรับเมื่อต้องการเน้นรายละเอียดเท่านั้น
อ้างอิง
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/setInfinity.html
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/playbackOptions.html
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-619CAE9C-107D-4504-A769-227DDC847153-htm.html
https://ja.wikipedia.org/wiki/ドラゴンボールの技一覧#.E5.85.83.E6.B0.97.E7.8E.89
http://help.autodesk.com/cloudhelp/2016/JPN/Maya-Tech-Docs/CommandsPython/playbackOptions.html
https://knowledge.autodesk.com/ja/support/maya/learn-explore/caas/CloudHelp/cloudhelp/2016/JPN/Maya/files/GUID-619CAE9C-107D-4504-A769-227DDC847153-htm.html
https://ja.wikipedia.org/wiki/ドラゴンボールの技一覧#.E5.85.83.E6.B0.97.E7.8E.89