ในบทที่ผ่านๆมาได้พูดถึงการสร้างรูปทรงต่างๆและทำให้ย่อขยายเปลี่ยนรูปไปได้ ในระดับนึง แต่ว่าก็ยังมีข้อจำกัดของรูปร่างที่ทำได้ เพราะยังอยู่ในขอบเขตของรูปทรงเริ่มต้น ไม่สามารถแก้ไขอะไรได้มากนัก

สำหรับในบทนี้จะพูดถึงการเปลี่ยนแปลงที่โครงสร้างภายใน ซึ่งจะทำให้สามารถเปลี่ยนแปลงรูปร่างของวัตถุได้อย่างอิสระมากขึ้น

วัตถุประเภทโพลิกอนโดยทั่วไปประกอบขึ้นจากจุดยอด (頂点, vertex) ต่างๆ โดยมีเส้นลากระหว่างจุดสองจุดเกิดเป็นเส้นขอบ (エッジ, edge) และเส้นขอบสามอันขึ้นไปล้อมกันเกิดเป็นหน้า (フェース, face) ขึ้น

จำนวน ของจุดยอด เส้นขอบ และหน้า สามารถหาได้โดยใช้ฟังก์ชัน polyEvaluate() โดยใส่แฟล็กต่างกันได้แก่ v (vertex), e (edge) และ f (face)
v=1 เป็นการหาจำนวนจุดยอด
e=1 เป็นการหาจำนวนเส้นขอบ
f=1 เป็นการหาจำนวนหน้า

ชื่อวัตถุที่ต้องการหาค่านั้นให้ใส่เป็นอาร์กิวเมนต์ของฟังก์ชัน แต่หากไม่ใส่ชื่อวัตถุจะเป็นการหาค่าของวัตถุที่ถูกเลือกอยู่

ยกตัวอย่างทรงสี่เหลี่ยม
จะเห็นว่าทรงสี่เหลี่ยมที่ไม่มีการแบ่งส่วนย่อยเลยจะประกอบไปด้วย 8 จุดยอด 12 เส้นขอบ และ 6 หน้า



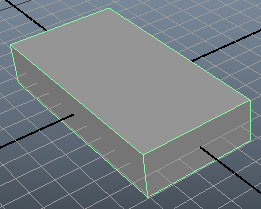
การเข้าถึงจุดยอดแต่ละอันภายในวัตถุทำได้โดยการใส่ชื่อวัตถุแล้วตามด้วย .vtx[หมายเลข]

ลองพิมพ์
ก็จะเห็นว่าทรงสี่เหลี่ยมที่ถูกสร้างขึ้นนั้นถูกเลือกที่ตัวจุดยอดจุดหนึ่งอยู่



หมายเลขของจุดจะไล่ตั้งแต่ 0 ไปจนถึงเท่ากับจำนวนจุดยอดลบด้วย 1 ดังนั้นสำหรับทรงสี่เหลี่ยมจะประกอบไปด้วย
.vtx[0] .vtx[1] ไปเรื่อยๆถึง .vtx[7]

หากต้องการเลือกพร้อมกันหลายอันที่มีเลขติดกันก็ทำได้โดยใช้ : เช่น
จะเป็นการเลือกจุดยอดพร้อมกัน ๔ อัน



และถ้าอยากเลือกจุดยอดทั้งหมดก็ทำได้โดยใช้ * เช่น
จุดยอดทุกจุดจะถูกเลือก



สำหรับเส้นขอบสามารถเข้าถึงได้โดยชื่อวัตถุตามด้วย .e[หมายเลข] ส่วนหน้าก็จะเป็น .f[หมายเลข]

สำหรับทรงสี่เหลี่ยมจะมีเส้นขอบ ๑๒ อัน และมีหน้า ๖ หน้า ก็จะประกอบด้วย
.e[0] .e[1] ไปจนถึง .e[11]
.f[0] .f[1] ไปจนถึง .f[5]

โดยที่เส้นขอบหรือหน้าไหนจะเป็นเลขอะไรนั้นก็มีกำหนดตายตัวอยู่แล้วโดยอัตโนมัติ สามารถรู้ได้จากการลองกดเลือกดูแล้วสังเกตเอาได้ รูปทรงแต่ละชนิดก็กำหนดต่างกันออกไป

นอกจากแค่เลือกด้วย select() แล้วยังอาจใช้กังฟังก์ชันอื่นเช่น delete() เพื่อลบ
จะได้ทรงสี่เหลี่ยมที่ถูกลบหน้าไป ๓ หน้า เหลือแค่ ๓ หน้า



ต้องระวังอย่างหนึ่งว่าหากลบหน้าไปแล้ว ตัวเลขชี้หน้าอื่นๆที่เหลืออาจเปลี่ยนแปลงไปหมดได้ ดังนั้นหลังจากลบไปแล้วจะทำอะไรต่อต้องดูเลขชี้หน้าใหม่ทุกครั้ง

ลองสร้างทรงสี่เหลี่ยมขึ้นมาแล้วพิมพ์ mc.delete('.f[0]') ซ้ำไปเรื่อยๆ จะพบว่าหน้าค่อยๆหายไปทีละหน้า ที่เป็นแบบนี้เพราะพอกดลบห้าน .f[0] ไปก็จะมีหน้าอื่นกลายเป็น .f[0] แทน เพราะเป็นเลขตัวแรก ต่อให้เหลือหน้าเดียวยังไงก็ต้องมีวัตถุชื่อ .f[0] แน่นอน

ดังนั้นหากพิมพ์ mc.delete('.f[0]') ไป ๕ ครั้งก็จะเหลือแค่หน้าเดียว อย่างไรก็ตามจะไม่สามารถลบหน้าทั้งหมดจนเหลือศูนย์หน้าได้ หากจะลบก็ทำการลบทั้งวัตถุไปเลย



ด้วยการจัดการกับส่วนประกอบทีละตัวเราสามารถเปลี่ยนแปลงรูปร่างของของวัตถุได้อย่างอิสระ เช่นอาศัยการย้ายจุดยอด

ลองสร้างทรงสี่เหลี่ยมขึ้นมาแล้วย้ายมุมหนึ่งไปจะได้รูปร่างที่แปลกออกไป


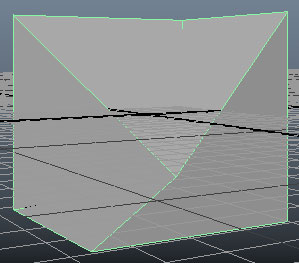
หรืออาจทำการย้ายเส้นขอบ ซึ่งก็จะเป็นการย้ายจุดยอดที่เป็นส่วนประกอบของเส้นขอบนั้นพร้อมกันสองจุด หรือถ้าย้ายหน้าก็จะเป็นการย้ายจุดที่เป็นส่วนประกอบของหน้านั้นทั้งหมดที เดียว

อาจทำการหมุนหรือย่อขยายส่วนประกอบเพื่อเคลื่อนย้าย

คำสั่ง move(), rotate() และ scale() เมื่อใช้กับส่วนประกอบย่อยของวัตถุจะเป็นการเคลื่อนย้ายจุดยอดต่างๆ ไม่ใช่การเปลี่ยนแปลงค่าองค์ประกอบต่างๆเช่นมุมหมุนหรือมาตราส่วน

เช่นการใช้ scale() ถ้าค่าน้อยกว่าหนึ่งจะเป็นการลดระยะห่างระหว่างจุดลง ถ้ามากกว่าหนึ่งจะเป็นการเคลื่อนให้ห่างไปมากขึ้น
จะได้รูปดาว



ลองสร้างทรงกระบอกแล้วจับมาหมุนบิด


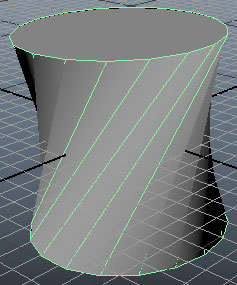
อาจใช้ for เพื่อเข้าถึงส่วนประกอบหลายๆตัว ทำออกมาเป็นรูปสวยๆได้


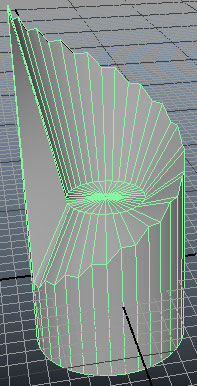
หากต้องการเข้าถึงด้านทั้งหมดเพื่อทำอะไรก็อาจใช้ for โดยหาขอบเขตด้วย polyEvaluate() เช่นลอง
ก็จะได้พื้นผิวลูกคลื่นสวยๆมา



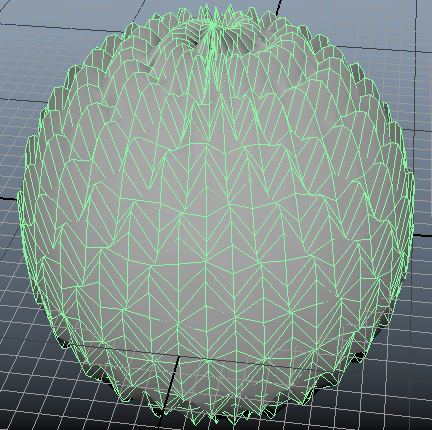
หรือทรงกลมหน้าตาคล้ายผลไม้ที่มีผิวขรุขระ




จบบทนี้ไปแล้วเราสามารถสร้างรูปทรงที่หลากหลายได้มากมาย ไม่จำกัดแค่เพียงรูปทรงพื้นฐานอีกต่อไปแล้ว



อ้างอิง

<< บทที่แล้ว      บทถัดไป >>
หน้าสารบัญ

~ 自己紹介 ~

目次

日本による名言集

python モジュール -- numpy -- matplotlib -- pandas -- manim -- opencv -- pyqt -- pytorch 機械学習 -- ニューラル      ネットワーク

javascript

モンゴル語

言語学

maya

確率論

日本での日記

中国での日記 -- 北京での日記 -- 香港での日記 -- 澳門での日記

台灣での日記

北欧での日記

他の国での日記

qiita

その他の記事

記事の類別

==เลือกหมวด== ดาราศาสตร์ คณิตศาสตร์ -ความน่าจะเป็น คอมพิวเตอร์ -เขียนโปรแกรม --python ---numpy ---scipy ---matplotlib ---pandas ---manim ---pyqt ---sklearn ---pytorch ---mayapython --ruby --javascript --dart --sql --regex --opencv -shell -3D --maya --MMD -microsoft_office -pdf -ปัญญาประดิษฐ์ --โครงข่ายประสาทเทียม -การสุ่ม ภาษาศาสตร์ -ตัวอักษร -เรียนภาษา -หลักเกณฑ์การทับศัพท์ -ภาษาจีน --ภาษาจีนกลาง -ภาษาญี่ปุ่น -ภาษามองโกล -ภาษาลาว -ภาษาเขมร ประวัติศาสตร์ -ประวัติศาสตร์จีน -ประวัติศาสตร์ญี่ปุ่น ปรัชญา บันทึก เรื่องแต่ง ประเทศจีน -จีนแผ่นดินใหญ่ --ปักกิ่ง --เทียนจิน --เหลียวหนิง --เหอเป่ย์ --เหอหนาน --ซานตง --ซานซี --อานฮุย --เจ้อเจียง --หูเป่ย์ --หูหนาน --ฝูเจี้ยน --กวางตุ้ง ---แต้จิ๋ว --ยูนนาน --ซินเจียง -ฮ่องกง -มาเก๊า -ไต้หวัน --ไทเป --จีหลง --เถาหยวน --ซินจู๋ --เหมียวลี่ --ไถจง --จางฮว่า --หยวินหลิน --เจียอี้ --ไถหนาน --เกาสยง --ผิงตง --อี๋หลาน ประเทศญี่ปุ่น -ฮกไกโด -อาโอโมริ -อิวาเตะ -มิยางิ -อากิตะ -ยามางาตะ -ฟุกุชิมะ -อิบารากิ -โทจิงิ -กุมมะ -ไซตามะ -จิบะ -โตเกียว -คานางาวะ -นีงาตะ -โทยามะ -อิชิกาวะ -ฟุกุอิ -ยามานาชิ -นางาโนะ -กิฟุ -ชิซึโอกะ -ไอจิ -มิเอะ -ชิงะ -เกียวโต -โอซากะ -เฮียวโงะ -นาระ -วากายามะ -โอกายามะ -ฮิโรชิมะ -ยามางุจิ -ฟุกุโอกะ ต่างแดน -อุษาคเนย์ --กัมพูชา --พม่า --สิงคโปร์ -ยุโรป --สวีเดน --เดนมาร์ก --ฟินแลนด์ ท่องเที่ยว -มหาวิทยาลัย -พิพิธภัณฑ์ --พิพิธภัณฑ์วิทยาศาสตร์ --หอศิลป์ -สวนสัตว์ --พิพิธภัณฑ์สัตว์น้ำ -ท้องฟ้าจำลอง -ตึกระฟ้า -ปราสาท☑ --ปราสาทญี่ปุ่น --ปราสาทขอม --ปราสาทยุโรป -ศาสนสถาน --วัด --ศาลเจ้า --โบสถ์ --มัสยิด -สุสาน -มรดกโลก -ทะเล -ทะเลสาบ -ภูเขา -หิมะ -ดอกซากุระ -แมว -รถไฟ -เรือ -ตลาดกลางคืน -งานเทศกาล -ที่ระลึกภัยพิบัติ -ตามรอย บันเทิง -เกม --อาเตอลีเย --โปเกมอน --caligula --vn -อนิเมะ -มังงะ -นิยาย -เพลง --เพลงอนิเมะ --เพลงเกม

　 記事を検索

　 最新記事

　 おすすめの記事

月別記事

もっと前の記事

ไทย

日本語

中文