โครงข่ายประสาทเทียมเบื้องต้น บทที่ ๑: เพอร์เซปตรอนชั้นเดียว
เขียนเมื่อ 2018/08/26 23:20
แก้ไขล่าสุด 2022/07/10 21:14
ในบทนำได้แนะนำแนวคิดและภาพรวมทั่วไปเกี่ยวกับโครงข่ายประสาทเทียมไปแล้ว
สำหรับในส่วนนี้จะเริ่มเข้าสู่เนื้อหาหลักที่มีการคำนวณ และวิธีการเขียนโปรแกรมภาษาไพธอนขึ้นเพื่อใช้งานจริง
โดยจะเริ่มแนะนำจากโครงสร้างที่เรียบง่ายที่สุดอย่างเพอร์เซปตรอนชั้นเดียว แล้วจึงต่อยอดไปสู่เพอร์เซปตรอนหลายชั้น แล้วปิดท้ายด้วยโครงข่ายประสาทแบบคอนโวลูชัน (CNN)
ความรู้พื้นฐานที่ควรจะมีคือ
- เวกเตอร์: เข้าใจวิธีบวกลบและด็อตเวกเตอร์
- เมทริกซ์: เข้าใจวิธีบวกลบคูณเมทริกซ์
- พื้นฐานแคลคูลัส: เข้าใจวิธีหาอนุพันธ์ โดยเฉพาะอนุพันธ์ย่อย ส่วนปริพันธ์ไม่ต้องใช้จึงไม่จำเป็น
- พื้นฐานไพธอน: อ่านบทเรียนไพธอนพื้นฐานอย่างน้อยถึงบทที่ ๒๒ ใน https://phyblas.hinaboshi.com/saraban/python
- พื้นฐาน numpy: อ่านบทที่ ๒,๓,๔,๑๕,๒๗,๒๑,๒๓ ใน https://phyblas.hinaboshi.com/saraban/numpy_matplotlib
เพียงแต่โค้ดตรงไหนที่ใช้คำสั่งที่เข้าใจยากจะมีการอธิบายละเอียดอีกที ดังนั้นรู้แค่คร่าวๆไว้ก็อาจเพียงพอ
นอกจากนี้ในนี้มีการวาดภาพแสดงผลด้วย matplotlib แต่เนื่องจากไม่ใช่จุดสำคัญที่ต้องเน้นจึงจะแค่ลงโค้ดไว้ ถ้าใครเข้าใจ matplotlib ก็จะดีกว่า แต่ไม่ได้ขาดไม่ได้
การเขียนจะใช้ไพธอน มอดูลที่ต้องการมีเพียง numpy และ matplotlib ไม่ได้ใช้อย่างอื่นเลย
โค้ดถูกเขียนเพื่อใช้สำหรับไพธอน 3 เป็นหลัก แต่ก็ใช้ในไพธอน 2 ได้เช่นกัน
เพอร์เซปตรอน
เพอร์เซปตรอน (感知器, perceptron) ถือเป็นจุดเริ่มต้นของโครงข่ายประสาทเทียมในยุคแรกสุด ถูกคิดค้นขึ้นในปี 1957
โครงสร้างมีลักษณะง่ายๆคือเป็นเซลล์ประสาทจำลองเซลล์หนึ่งที่รับสัญญาณจำนวนหนึ่งมาจากชั้นขาเข้าซึ่งอาจมีหลายช่องทาง เซลล์จะทำการพิจารณาว่าสัญญาณทั้งหมดรวมแล้วเกินค่าค่าหนึ่งหรือไม่ ถ้าเกินก็จะทำการส่งสัญญาณต่อไป ค่าที่เป็นตัวแบ่งนั้นเรียกว่าค่าขีดแบ่ง (阈值, threshold)
เพียงแต่ว่าข้อมูลต่างๆที่ป้อนเข้าไปจะมีน้ำหนักความสำคัญไม่เท่ากัน โดยจะมีการคูณด้วยค่าน้ำหนัก (权重, weight) ก่อนจึงค่อยนำมาบวกกัน เขียนเป็นสมการจะได้ว่า
..(1.1)
โดย x1, x2, ... คือข้อมูลป้อนเข้า w1, w2, ... เป็นค่าน้ำหนักที่มาคูณค่าของข้อมูลนั้น ส่วน θ คือค่าขีดแบ่ง
ถ้าผลคูณรวมแล้วได้ค่าถึง θ ก็จะได้ค่าเป็น 1 ซึ่งหมายถึงมีสัญญาณไหล แต่ถ้าไม่ถึงก็จะได้ค่า 0 หมายถึงไม่มีสัญญาณไหลผ่าน
เขียนเป็นภาพได้ดังนี้
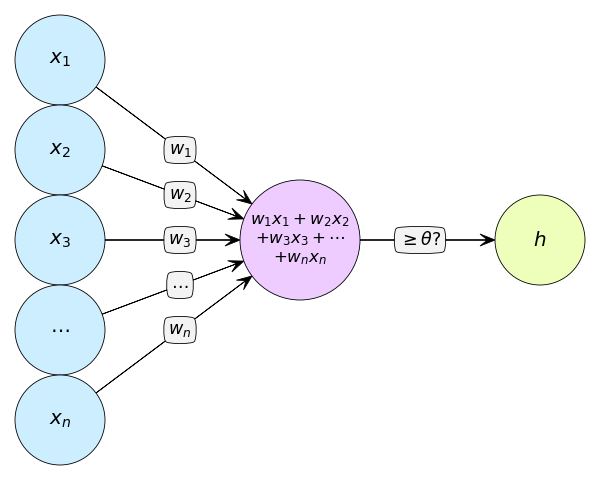
h คือผลลัพธ์ที่ได้ ซึ่งจะมีค่า 1 หรือ 0
เพียงแต่ว่าโดยทั่วไปแล้วแทนที่จะเขียนในรูปของค่าขีดแบ่ง กลับมักจะถูกเขียนในรูปของค่าไบแอส (偏差, bias) มากกว่า คือ
..(1.2)
และ
..(1.3)
ในที่นี้ b เรียกว่าค่าไบแอส ซึ่งจะเห็นว่า b = -θ
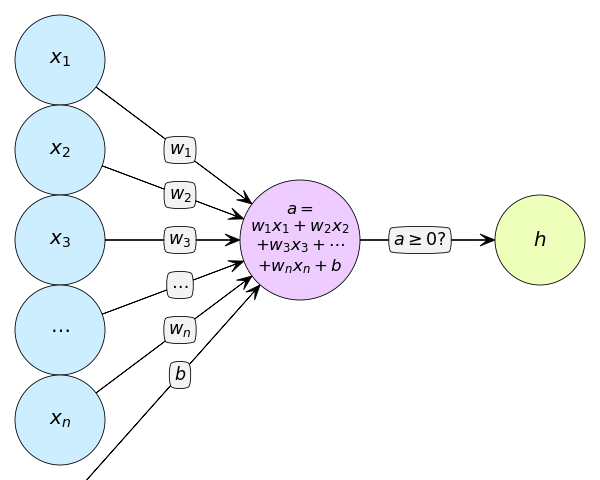
การเขียนในรูปค่าไบแอสแบบนี้สะดวกกว่า เพราะแค่สร้างฟังก์ชันอันนึงขึ้นมา (ในที่นี้แทนด้วย a) แล้วเอามันมาเปรียบเทียบกับค่า 0
ถ้าผลคูณรวมบวกไบแอสแล้วค่าถึง 0 ขึ้นไปก็จะได้ค่าเป็น 1 คือมีการสร้างสัญญาณไหลผ่าน
แต่ถ้าน้อยกว่า 0 จะได้ค่าเป็น 0 คือไม่มีการสร้างสัญญาณไหลผ่าน
ค่า w และ b ในที่นี้เรียกว่าเป็นค่าพารามิเตอร์ (参数, parameter) ของเพอร์เซปตรอน เป็นค่าที่จะต้องปรับให้เหมาะสมกับปัญหาที่พิจารณา
เพื่อให้เห็นภาพชัดต่อไปจะเป็นการยกตัวอย่าง
สมมุติว่าเด็กคนหนึ่งต้องการซื้อของราคา 1000 บาท เขาลองเปิดกระเป๋าตังค์ตัวเองดูก็พบว่ามีอยู่แค่ธนบัตรใบละ 20 กับ 50 บาทเท่านั้น ถามว่าเขาต้องมีธนบัตรใบละเท่าไหร่อยู่กี่ใบจึงจะซื้อได้?
สำหรับปัญหาข้อนี้ถ้าให้ x1 เป็นจำนวนธนบัตร 20 บาทและ x2 เป็นจำนวน 50 บาท จะได้ว่า w1 คือ 20 และ w2 คือ 50 ส่วนไบแอส b ก็เท่ากับ -1000
ดังนั้นสมการ (1.2) จะได้
..(1.4)
อาจเขียนแผนภาพได้แบบนี้
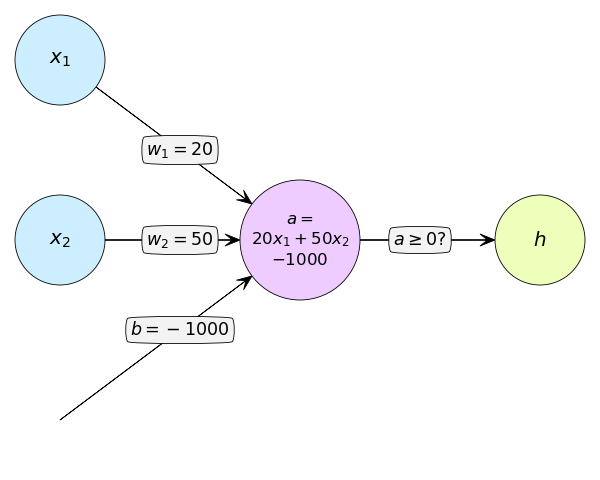
สมมุติว่าเราต้องการเขียนโปรแกรมในรูปแบบของเพอร์เซปตรอนเพื่อคำนวณแล้วตอบคำถามข้อนี้จะได้แบบนี้
วิธีการเขียนข้างต้นนี้เขียนขึ้นในแบบที่ให้ดูง่าย ตรงไปตรงมา แต่ต่อจากนี้ไปเพื่อความสะดวกในการคำนวณจริงๆจะเขียนในรูปอาเรย์ของ numpy เป็นแบบนี้
โดยทั้ง x และ w เป็นปริมาณที่มีหลายตัวดังนั้นจึงสะดวกที่จะเขียนในรูปของอาเรย์ โดยในที่นี้
X = [x1,x2]
w = [w1,w2]
อนึ่ง ในบทความชุดนี้จะใช้ X ตัวใหญ่แบบนี้ภายในโค้ดเพื่อแสดงข้อมูลตัวแปรต้นหลายมิติ แต่เวลาเขียนสมการจะใช้ x ตัวเล็กเสมอ
ส่วนไบแอส b มีตัวเดียวอยู่แล้วก็ไม่ต้องไปทำอะไร
ตอนที่คำนวณ a ก็แค่นำอาเรย์มาคูณกันแล้วก็รวมทั้งหมด แล้วค่อยไปบวก b อีกที
ในที่นี้มีจำนวนตัวแปรต้นและน้ำหนักอยู่ ๒ ตัว แต่หากกำหนดแบบนี้แล้วตัวแปรต้น x จะมีกี่ตัวก็ได้ แค่ w ต้องมีจำนวนเท่านั้นตาม
การคำนวณในแบบอาเรย์
โครงข่ายประสาทนั้นประกอบด้วยการคำนวณที่ซับซ้อน และเพื่อที่จะทำให้การคำนวณเป็นไปอย่างประสิทธิภาพ โดยทั่วไปทุกอย่างจะถูกทำอยู่ในรูปของอาเรย์ หรือก็คือเมทริกซ์
ดังนั้นแล้วเพื่อที่จะไปต่อได้จำเป็นต้องอาศัยความเข้าใจเรื่องเมทริกซ์ค่อนข้างดี หากใครยังพื้นฐานตรงนี้ไม่ดีจำเป็นจะต้องไปทวน
จากตัวอย่างที่แล้วเราเขียน x ในรูปของข้อมูลที่มีหลายตัวแปร ดังนั้น x จึงอยู่ในรูปของอาเรย์หนึ่งมิติ
อย่างไรก็ตามโดยทั่วไปเวลาคำนวณเราจะไม่ได้มีข้อมูลป้อนเข้าแค่ค่าเดียวแต่มาเป็นชุดๆหลายตัว
นั่นคือเราจะมีข้อมูลหลายตัว และแต่ละตัวก็เป็นข้อมูลหลายตัวแปร ดังนั้นเมื่อต้องการเขียนข้อมูลทั้งหมดทีเดียว จะได้ว่าอยู่ในรูปของอาเรย์สองมิติ
..(1.5)
โดย n คือจำนวนข้อมูล ส่วน m คือจำนวนตัวแปร
อนึ่ง เนื่องจากอาเรย์ในไพธอนจะเริ่มนับจาก 0 เพื่อความง่ายแล้วต่อจากนี้จะเริ่มนับเลขไล่ตั้งแต่ 0 แทนที่จะเริ่มจาก 1
และค่า a ก็จะมีหลายค่าเหมือนกัน สามารถเขียนสูตรการคำนวณในรูปการคูณเมทริกซ์ได้โดย
..(1.6)
ที่ใช้อักษรเป็นตัวหนาตรงนี้คือแสดงถึงว่าเป็นอาเรย์สองมิติ (เมทริกซ์) ไม่ใช่ตัวแปรที่เป็นเลขตัวเดียว ส่วนตัวแปรที่มีลูกศรอยู่ด้านบนจะหมายถึงอาเรย์หนึ่งมิติ (เวกเตอร์) ในขณะที่ถ้าเป็นตัวเอียงธรรมดาจะหมายถึงค่าเลขตัวเดียว ในบทความชุดนี้ทั้งหมดจะใช้วิธีการเขียนแบบนี้ในสมการเพื่อแยกแยะให้ชัดเจน
เครื่องหมายจุดตรงกลาง ⋅ ในที่นี้คือการคูณเมทริกซ์ โดยใน numpy จะใช้คำสั่ง np.dot() ไม่ใช่การคูณกันแบบคูณอาเรย์ธรรมดาซึ่งจะเป็นการนำสมาชิกทั้งหมดมาคูณกันเฉยๆ
โดย w ในที่นี้เป็นอาเรย์หนึ่งมิติ โดยอาเรย์หนึ่งมิติปกติจะเขียนเรียงในแนวตั้ง
..(1.7)
และจะได้ว่า
..(1.8)
a ของแต่ละตัวคือ
..(1.9)
ทีนี้จะสามารถเขียนฟังก์ชันของเพอร์เซปตรอนใหม่เพื่อให้สามารถคำนวณได้พร้อมกันทีละหลายตัว แบบนี้
จากนั้นลองนำมาใช้กับอาเรย์ค่า x ที่เป็นสองมิติได้แบบนี้
เท่ากับเป็นการคำนวณหาคำตอบใน ๓ กรณีในคราวเดียวเลย ซึ่งการทำแบบนี้นอกจากการเขียนจะดูกะทัดรัดกว่าแล้วยังคำนวณเร็วกว่ามากด้วย
อนึ่ง .astype(int) ในที่นี้ทำเพื่อเปลี่ยนค่าที่เดิมทีควรจะอยู่ในรูป True,False ให้เป็น 1,0 แต่ที่จริงในกรณีส่วนใหญ่ต่อให้ไม่เปลี่ยนก็สามารถใช้คำนวณได้เหมือนกัน
เราสามารถเขียนโปรแกรมให้ทำการวาดภาพแสดงการแบ่งอาณาเขตระหว่างส่วนที่เป็น 0 และ 1 ได้โดยเขียนแบบนี้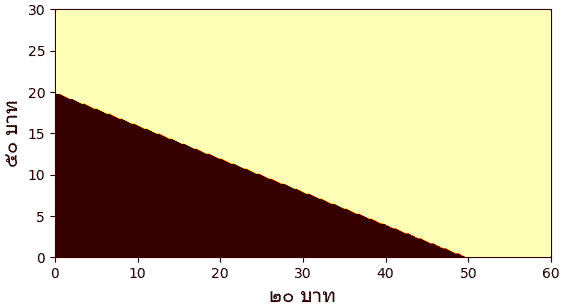
สีดำเป็นเขตที่ได้ 0 สีเหลืองคือได้ 1 จะเห็นว่าถ้ามีแค่ธนบัตรใบละ 20 อย่างเดียวสัก 50 ใบก็ซื้อของได้ หรือมีใบละ 50 สัก 20 ใบก็ซื้อได้เหมือนกัน สมเหตุสมผล
สำหรับวิธีการวาดภาพนั้นใช้ matplotlib ซึ่งไม่ใช่เนื้อหาที่ต้องเน้นตรงนี้จึงจะไม่อธิบายรายละเอียด จะลงแค่โค้ดไว้ หากใครต้องการเข้าใจว่าทำงานยังไงให้อ่านรายละเอียดในเนื้อหา "numpy & matplotlib เบื้องต้น" ในบล็อกนี้
ลอจิกเกต
เพื่อให้เข้าใจมากขึ้นจะขอยกตัวอย่างเพิ่มเติมอีก
ตัวอย่างหนึ่งที่มักถูกยกมาใช้กันมากคือเกต OR เกต AND ในวงจรตรรกะซึ่งถูกใช้บ่อยในเรื่องของวงจรอิเล็กทรอนิกส์
เกี่ยวกับเรื่องนี้หากใครยังไม่เคยรู้จักคุ้นเคยมาก่อนอาจรายละเอียดอ่านได้ในวิกิ https://th.wikipedia.org/wiki/ประตูสัญญาณตรรกะ
ลอจิกเกตในวงจรอิเล็กทรอนิกส์นั้นโดยปกติจะรับสัญญาณเข้ามาทีละ ๒ ตัวแล้ว
เกต OR เป็นเกตที่จะให้ค่า 1 ถ้ามีตัวใดตัวหนึ่งเป็น 1 แต่ถ้าเป็น 0 ทั้งคู่จึงจะเป็น 0
เราอาจเขียนฟังก์ชันสำหรับทำเกต OR ได้ดังนี้
ซึ่งในความเป็นจริงแล้วค่า b และ w ที่ทำเกต OR ได้ตามที่ต้องการนั้นไม่ได้มีเพียงหนึ่งเดียว เช่น b จะปรับเป็น -0.1 หรือ -1 ก็ยังคงได้คำตอบแบบเดิม เพราะยังไงข้อมูลป้อนเข้าก็มีอยู่ได้เพียง ๔ รูปแบบดังที่ยกมา ขอแค่แบ่งทั้ง ๔ แบบได้ตามเงื่อนไขที่ยกมาก็ถือว่าใช้ได้แล้ว
ถ้าวาดแสดงเป็นภาพก็จะได้แบบนี้
ถ้าปรับค่าใน h เป็น w = np.array([0.5,2]) และ b = -0.4 ก็จะได้เขตการแบ่งที่เปลี่ยนไปแต่ก็ยังสามารถแบ่งค่าตามที่ต้องการได้อยู่
ตรงนี้ประเด็นสำคัญที่ต้องการจะให้เห็นก็คือ เราจะเห็นว่าเมื่อค่าพารามิเตอร์ต่างๆในเพอร์เซปตรอนเป็นค่าที่เหมาะสมแล้วผลลัพธ์ก็จะออกมาตามที่ควรจะเป็น
ว่าแต่ว่าจะทำยังไงให้ได้ค่าพารามิเตอร์เหล่านี้มา? นี่ล่ะคือประเด็นสำคัญ
ความจริงแล้วก็คือ เวลาใช้งานจริงๆพารามิเตอร์เหล่านี้ผู้เขียนโปรแกรมจะไม่ได้เป็นคนใส่ให้ แต่โปรแกรมจะทำการเรียนรู้จากข้อมูลที่ใส่เข้าไปเพื่อหาค่าเหล่านี้เอง
เพราะเป็นเช่นนั้นเพอร์เซปตรอนจึงถูกเรียกว่าเป็นเทคนิคการเรียนรู้ของเครื่อง ไม่เช่นนั้นมันก็จะเป็นแค่ฟังก์ชันธรรมดาที่ไม่มีการเรียนรู้
ในบทต่อไปจะกล่าวถึงวิธีการในการเรียนรู้เพื่อปรับพารามิเตอร์
>> อ่านต่อ บทที่ ๒
สำหรับในส่วนนี้จะเริ่มเข้าสู่เนื้อหาหลักที่มีการคำนวณ และวิธีการเขียนโปรแกรมภาษาไพธอนขึ้นเพื่อใช้งานจริง
โดยจะเริ่มแนะนำจากโครงสร้างที่เรียบง่ายที่สุดอย่างเพอร์เซปตรอนชั้นเดียว แล้วจึงต่อยอดไปสู่เพอร์เซปตรอนหลายชั้น แล้วปิดท้ายด้วยโครงข่ายประสาทแบบคอนโวลูชัน (CNN)
ความรู้พื้นฐานที่ควรจะมีคือ
- เวกเตอร์: เข้าใจวิธีบวกลบและด็อตเวกเตอร์
- เมทริกซ์: เข้าใจวิธีบวกลบคูณเมทริกซ์
- พื้นฐานแคลคูลัส: เข้าใจวิธีหาอนุพันธ์ โดยเฉพาะอนุพันธ์ย่อย ส่วนปริพันธ์ไม่ต้องใช้จึงไม่จำเป็น
- พื้นฐานไพธอน: อ่านบทเรียนไพธอนพื้นฐานอย่างน้อยถึงบทที่ ๒๒ ใน https://phyblas.hinaboshi.com/saraban/python
- พื้นฐาน numpy: อ่านบทที่ ๒,๓,๔,๑๕,๒๗,๒๑,๒๓ ใน https://phyblas.hinaboshi.com/saraban/numpy_matplotlib
เพียงแต่โค้ดตรงไหนที่ใช้คำสั่งที่เข้าใจยากจะมีการอธิบายละเอียดอีกที ดังนั้นรู้แค่คร่าวๆไว้ก็อาจเพียงพอ
นอกจากนี้ในนี้มีการวาดภาพแสดงผลด้วย matplotlib แต่เนื่องจากไม่ใช่จุดสำคัญที่ต้องเน้นจึงจะแค่ลงโค้ดไว้ ถ้าใครเข้าใจ matplotlib ก็จะดีกว่า แต่ไม่ได้ขาดไม่ได้
การเขียนจะใช้ไพธอน มอดูลที่ต้องการมีเพียง numpy และ matplotlib ไม่ได้ใช้อย่างอื่นเลย
โค้ดถูกเขียนเพื่อใช้สำหรับไพธอน 3 เป็นหลัก แต่ก็ใช้ในไพธอน 2 ได้เช่นกัน
เพอร์เซปตรอน
เพอร์เซปตรอน (感知器, perceptron) ถือเป็นจุดเริ่มต้นของโครงข่ายประสาทเทียมในยุคแรกสุด ถูกคิดค้นขึ้นในปี 1957
โครงสร้างมีลักษณะง่ายๆคือเป็นเซลล์ประสาทจำลองเซลล์หนึ่งที่รับสัญญาณจำนวนหนึ่งมาจากชั้นขาเข้าซึ่งอาจมีหลายช่องทาง เซลล์จะทำการพิจารณาว่าสัญญาณทั้งหมดรวมแล้วเกินค่าค่าหนึ่งหรือไม่ ถ้าเกินก็จะทำการส่งสัญญาณต่อไป ค่าที่เป็นตัวแบ่งนั้นเรียกว่าค่าขีดแบ่ง (阈值, threshold)
เพียงแต่ว่าข้อมูลต่างๆที่ป้อนเข้าไปจะมีน้ำหนักความสำคัญไม่เท่ากัน โดยจะมีการคูณด้วยค่าน้ำหนัก (权重, weight) ก่อนจึงค่อยนำมาบวกกัน เขียนเป็นสมการจะได้ว่า
..(1.1)
โดย x1, x2, ... คือข้อมูลป้อนเข้า w1, w2, ... เป็นค่าน้ำหนักที่มาคูณค่าของข้อมูลนั้น ส่วน θ คือค่าขีดแบ่ง
ถ้าผลคูณรวมแล้วได้ค่าถึง θ ก็จะได้ค่าเป็น 1 ซึ่งหมายถึงมีสัญญาณไหล แต่ถ้าไม่ถึงก็จะได้ค่า 0 หมายถึงไม่มีสัญญาณไหลผ่าน
เขียนเป็นภาพได้ดังนี้

h คือผลลัพธ์ที่ได้ ซึ่งจะมีค่า 1 หรือ 0
เพียงแต่ว่าโดยทั่วไปแล้วแทนที่จะเขียนในรูปของค่าขีดแบ่ง กลับมักจะถูกเขียนในรูปของค่าไบแอส (偏差, bias) มากกว่า คือ
..(1.2)
และ
..(1.3)
ในที่นี้ b เรียกว่าค่าไบแอส ซึ่งจะเห็นว่า b = -θ

การเขียนในรูปค่าไบแอสแบบนี้สะดวกกว่า เพราะแค่สร้างฟังก์ชันอันนึงขึ้นมา (ในที่นี้แทนด้วย a) แล้วเอามันมาเปรียบเทียบกับค่า 0
ถ้าผลคูณรวมบวกไบแอสแล้วค่าถึง 0 ขึ้นไปก็จะได้ค่าเป็น 1 คือมีการสร้างสัญญาณไหลผ่าน
แต่ถ้าน้อยกว่า 0 จะได้ค่าเป็น 0 คือไม่มีการสร้างสัญญาณไหลผ่าน
ค่า w และ b ในที่นี้เรียกว่าเป็นค่าพารามิเตอร์ (参数, parameter) ของเพอร์เซปตรอน เป็นค่าที่จะต้องปรับให้เหมาะสมกับปัญหาที่พิจารณา
เพื่อให้เห็นภาพชัดต่อไปจะเป็นการยกตัวอย่าง
สมมุติว่าเด็กคนหนึ่งต้องการซื้อของราคา 1000 บาท เขาลองเปิดกระเป๋าตังค์ตัวเองดูก็พบว่ามีอยู่แค่ธนบัตรใบละ 20 กับ 50 บาทเท่านั้น ถามว่าเขาต้องมีธนบัตรใบละเท่าไหร่อยู่กี่ใบจึงจะซื้อได้?
สำหรับปัญหาข้อนี้ถ้าให้ x1 เป็นจำนวนธนบัตร 20 บาทและ x2 เป็นจำนวน 50 บาท จะได้ว่า w1 คือ 20 และ w2 คือ 50 ส่วนไบแอส b ก็เท่ากับ -1000
ดังนั้นสมการ (1.2) จะได้
..(1.4)
อาจเขียนแผนภาพได้แบบนี้

สมมุติว่าเราต้องการเขียนโปรแกรมในรูปแบบของเพอร์เซปตรอนเพื่อคำนวณแล้วตอบคำถามข้อนี้จะได้แบบนี้
def h(x1,x2):
w1 = 20
w2 = 50
b = -1000
a = w1*x1 + w2*x2 + b
if(a>=0):
return 1
else:
return 0
print(h(x1=20,x2=10)) # ได้ 0
print(h(x1=14,x2=15)) # ได้ 1วิธีการเขียนข้างต้นนี้เขียนขึ้นในแบบที่ให้ดูง่าย ตรงไปตรงมา แต่ต่อจากนี้ไปเพื่อความสะดวกในการคำนวณจริงๆจะเขียนในรูปอาเรย์ของ numpy เป็นแบบนี้
import numpy as np
def h(X):
w = np.array([20,50])
b = -1000
a = (w*X).sum() + b
return int(a>=0)
X = np.array([20,10])
print(h(X)) # ได้ 0
X = np.array([14,15])
print(h(X)) # ได้ 1โดยทั้ง x และ w เป็นปริมาณที่มีหลายตัวดังนั้นจึงสะดวกที่จะเขียนในรูปของอาเรย์ โดยในที่นี้
X = [x1,x2]
w = [w1,w2]
อนึ่ง ในบทความชุดนี้จะใช้ X ตัวใหญ่แบบนี้ภายในโค้ดเพื่อแสดงข้อมูลตัวแปรต้นหลายมิติ แต่เวลาเขียนสมการจะใช้ x ตัวเล็กเสมอ
ส่วนไบแอส b มีตัวเดียวอยู่แล้วก็ไม่ต้องไปทำอะไร
ตอนที่คำนวณ a ก็แค่นำอาเรย์มาคูณกันแล้วก็รวมทั้งหมด แล้วค่อยไปบวก b อีกที
ในที่นี้มีจำนวนตัวแปรต้นและน้ำหนักอยู่ ๒ ตัว แต่หากกำหนดแบบนี้แล้วตัวแปรต้น x จะมีกี่ตัวก็ได้ แค่ w ต้องมีจำนวนเท่านั้นตาม
การคำนวณในแบบอาเรย์
โครงข่ายประสาทนั้นประกอบด้วยการคำนวณที่ซับซ้อน และเพื่อที่จะทำให้การคำนวณเป็นไปอย่างประสิทธิภาพ โดยทั่วไปทุกอย่างจะถูกทำอยู่ในรูปของอาเรย์ หรือก็คือเมทริกซ์
ดังนั้นแล้วเพื่อที่จะไปต่อได้จำเป็นต้องอาศัยความเข้าใจเรื่องเมทริกซ์ค่อนข้างดี หากใครยังพื้นฐานตรงนี้ไม่ดีจำเป็นจะต้องไปทวน
จากตัวอย่างที่แล้วเราเขียน x ในรูปของข้อมูลที่มีหลายตัวแปร ดังนั้น x จึงอยู่ในรูปของอาเรย์หนึ่งมิติ
อย่างไรก็ตามโดยทั่วไปเวลาคำนวณเราจะไม่ได้มีข้อมูลป้อนเข้าแค่ค่าเดียวแต่มาเป็นชุดๆหลายตัว
นั่นคือเราจะมีข้อมูลหลายตัว และแต่ละตัวก็เป็นข้อมูลหลายตัวแปร ดังนั้นเมื่อต้องการเขียนข้อมูลทั้งหมดทีเดียว จะได้ว่าอยู่ในรูปของอาเรย์สองมิติ
..(1.5)
โดย n คือจำนวนข้อมูล ส่วน m คือจำนวนตัวแปร
อนึ่ง เนื่องจากอาเรย์ในไพธอนจะเริ่มนับจาก 0 เพื่อความง่ายแล้วต่อจากนี้จะเริ่มนับเลขไล่ตั้งแต่ 0 แทนที่จะเริ่มจาก 1
และค่า a ก็จะมีหลายค่าเหมือนกัน สามารถเขียนสูตรการคำนวณในรูปการคูณเมทริกซ์ได้โดย
..(1.6)
ที่ใช้อักษรเป็นตัวหนาตรงนี้คือแสดงถึงว่าเป็นอาเรย์สองมิติ (เมทริกซ์) ไม่ใช่ตัวแปรที่เป็นเลขตัวเดียว ส่วนตัวแปรที่มีลูกศรอยู่ด้านบนจะหมายถึงอาเรย์หนึ่งมิติ (เวกเตอร์) ในขณะที่ถ้าเป็นตัวเอียงธรรมดาจะหมายถึงค่าเลขตัวเดียว ในบทความชุดนี้ทั้งหมดจะใช้วิธีการเขียนแบบนี้ในสมการเพื่อแยกแยะให้ชัดเจน
เครื่องหมายจุดตรงกลาง ⋅ ในที่นี้คือการคูณเมทริกซ์ โดยใน numpy จะใช้คำสั่ง np.dot() ไม่ใช่การคูณกันแบบคูณอาเรย์ธรรมดาซึ่งจะเป็นการนำสมาชิกทั้งหมดมาคูณกันเฉยๆ
โดย w ในที่นี้เป็นอาเรย์หนึ่งมิติ โดยอาเรย์หนึ่งมิติปกติจะเขียนเรียงในแนวตั้ง
..(1.7)
และจะได้ว่า
..(1.8)
a ของแต่ละตัวคือ
..(1.9)
ทีนี้จะสามารถเขียนฟังก์ชันของเพอร์เซปตรอนใหม่เพื่อให้สามารถคำนวณได้พร้อมกันทีละหลายตัว แบบนี้
def h(X):
w = np.array([20,50])
b = -1000
a = np.dot(X,w) + b
return (a>=0).astype(int)จากนั้นลองนำมาใช้กับอาเรย์ค่า x ที่เป็นสองมิติได้แบบนี้
X = np.array([
[10,15],
[10,18],
[22,15]
])
print(h(X)) # ได้ [0 1 1]เท่ากับเป็นการคำนวณหาคำตอบใน ๓ กรณีในคราวเดียวเลย ซึ่งการทำแบบนี้นอกจากการเขียนจะดูกะทัดรัดกว่าแล้วยังคำนวณเร็วกว่ามากด้วย
อนึ่ง .astype(int) ในที่นี้ทำเพื่อเปลี่ยนค่าที่เดิมทีควรจะอยู่ในรูป True,False ให้เป็น 1,0 แต่ที่จริงในกรณีส่วนใหญ่ต่อให้ไม่เปลี่ยนก็สามารถใช้คำนวณได้เหมือนกัน
เราสามารถเขียนโปรแกรมให้ทำการวาดภาพแสดงการแบ่งอาณาเขตระหว่างส่วนที่เป็น 0 และ 1 ได้โดยเขียนแบบนี้
import matplotlib.pyplot as plt
mx,my = np.meshgrid(np.linspace(0,60,200),np.linspace(0,30,200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = h(mX).reshape(200,-1)
plt.axes(aspect=1)
plt.contourf(mx,my,mz,cmap='hot')
plt.xlabel(u'๒๐ บาท',family='Tahoma',size=14)
plt.ylabel(u'๕๐ บาท',family='Tahoma',size=14)
plt.show()
สีดำเป็นเขตที่ได้ 0 สีเหลืองคือได้ 1 จะเห็นว่าถ้ามีแค่ธนบัตรใบละ 20 อย่างเดียวสัก 50 ใบก็ซื้อของได้ หรือมีใบละ 50 สัก 20 ใบก็ซื้อได้เหมือนกัน สมเหตุสมผล
สำหรับวิธีการวาดภาพนั้นใช้ matplotlib ซึ่งไม่ใช่เนื้อหาที่ต้องเน้นตรงนี้จึงจะไม่อธิบายรายละเอียด จะลงแค่โค้ดไว้ หากใครต้องการเข้าใจว่าทำงานยังไงให้อ่านรายละเอียดในเนื้อหา "numpy & matplotlib เบื้องต้น" ในบล็อกนี้
ลอจิกเกต
เพื่อให้เข้าใจมากขึ้นจะขอยกตัวอย่างเพิ่มเติมอีก
ตัวอย่างหนึ่งที่มักถูกยกมาใช้กันมากคือเกต OR เกต AND ในวงจรตรรกะซึ่งถูกใช้บ่อยในเรื่องของวงจรอิเล็กทรอนิกส์
เกี่ยวกับเรื่องนี้หากใครยังไม่เคยรู้จักคุ้นเคยมาก่อนอาจรายละเอียดอ่านได้ในวิกิ https://th.wikipedia.org/wiki/ประตูสัญญาณตรรกะ
ลอจิกเกตในวงจรอิเล็กทรอนิกส์นั้นโดยปกติจะรับสัญญาณเข้ามาทีละ ๒ ตัวแล้ว
เกต OR เป็นเกตที่จะให้ค่า 1 ถ้ามีตัวใดตัวหนึ่งเป็น 1 แต่ถ้าเป็น 0 ทั้งคู่จึงจะเป็น 0
| x0 | x1 | z |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
เราอาจเขียนฟังก์ชันสำหรับทำเกต OR ได้ดังนี้
def h(X):
w = np.array([1,1])
b = -0.9
a = np.dot(X,w) + b
return (a>=0).astype(int)
X = np.array([
[0,0],
[0,1],
[1,0],
[1,1]
])
print(h(X)) # ได้ [0 1 1 1]ซึ่งในความเป็นจริงแล้วค่า b และ w ที่ทำเกต OR ได้ตามที่ต้องการนั้นไม่ได้มีเพียงหนึ่งเดียว เช่น b จะปรับเป็น -0.1 หรือ -1 ก็ยังคงได้คำตอบแบบเดิม เพราะยังไงข้อมูลป้อนเข้าก็มีอยู่ได้เพียง ๔ รูปแบบดังที่ยกมา ขอแค่แบ่งทั้ง ๔ แบบได้ตามเงื่อนไขที่ยกมาก็ถือว่าใช้ได้แล้ว
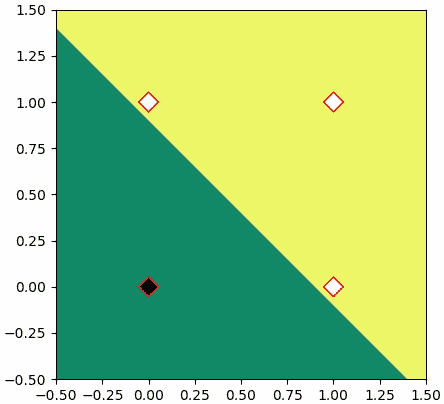
ถ้าวาดแสดงเป็นภาพก็จะได้แบบนี้
mx,my = np.meshgrid(np.linspace(-0.5,1.5,200),np.linspace(-0.5,1.5,200))
mX = np.array([mx.ravel(),my.ravel()]).T
mz = h(mX).reshape(200,-1)
plt.axes(aspect=1)
plt.contourf(mx,my,mz,cmap='summer')
plt.scatter(X[:,0],X[:,1],100,c=h(X),edgecolor='r',marker='D',cmap='hot')
plt.show()
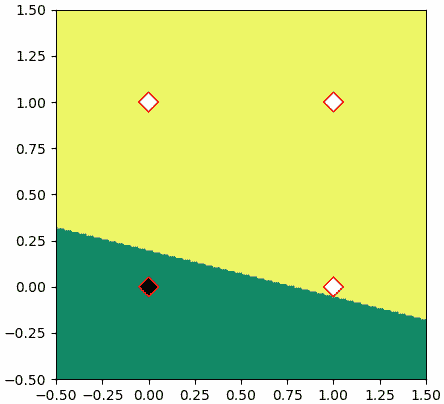
ถ้าปรับค่าใน h เป็น w = np.array([0.5,2]) และ b = -0.4 ก็จะได้เขตการแบ่งที่เปลี่ยนไปแต่ก็ยังสามารถแบ่งค่าตามที่ต้องการได้อยู่

ตรงนี้ประเด็นสำคัญที่ต้องการจะให้เห็นก็คือ เราจะเห็นว่าเมื่อค่าพารามิเตอร์ต่างๆในเพอร์เซปตรอนเป็นค่าที่เหมาะสมแล้วผลลัพธ์ก็จะออกมาตามที่ควรจะเป็น
ว่าแต่ว่าจะทำยังไงให้ได้ค่าพารามิเตอร์เหล่านี้มา? นี่ล่ะคือประเด็นสำคัญ
ความจริงแล้วก็คือ เวลาใช้งานจริงๆพารามิเตอร์เหล่านี้ผู้เขียนโปรแกรมจะไม่ได้เป็นคนใส่ให้ แต่โปรแกรมจะทำการเรียนรู้จากข้อมูลที่ใส่เข้าไปเพื่อหาค่าเหล่านี้เอง
เพราะเป็นเช่นนั้นเพอร์เซปตรอนจึงถูกเรียกว่าเป็นเทคนิคการเรียนรู้ของเครื่อง ไม่เช่นนั้นมันก็จะเป็นแค่ฟังก์ชันธรรมดาที่ไม่มีการเรียนรู้
ในบทต่อไปจะกล่าวถึงวิธีการในการเรียนรู้เพื่อปรับพารามิเตอร์
>> อ่านต่อ บทที่ ๒
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์ >> โครงข่ายประสาทเทียม-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy