[python] วิเคราะห์จำแนกประเภทข้อมูลด้วยต้นไม้ตัดสินใจ
เขียนเมื่อ 2017/11/05 21:39
แก้ไขล่าสุด 2022/07/21 15:02
ต้นไม้ตัดสินใจ (决策树, decision tree) เป็นเทคนิคหนึ่งในการเรียนรู้ของเครื่อง ซึ่งอาศัยการแตกเงื่อนไขย่อยไปเรื่อยๆเพื่อนำไปสู่คำตอบ
ชีวิตคนเรามักจะเผชิญกับทางเลือกอยู่เสมอ แล้วการเลือกนั้นก็อาจมีผลสำคัญทำให้เกิดผลลงเอยต่างกันออกไป
ยกตัวอย่างเช่น เราเลือกว่าจะอยู่บ้านหรือออกไปข้างนอก อยู่บ้านจะอ่านหนังสือหรือเล่นเกม ออกไปข้างนอกแล้วไปเจอเพื่อนหรือเปล่า เจอเพื่อนแล้วจะชวนกันไปเล่นเกมหรือไปอ่านหนังสือ แล้วสุดท้ายการกระทำเหล่านั้นจะเป็นตัวตัดสินว่าเราจะสอบปลายภาคผ่านหรือเปล่า
อาจเขียนแจกแจงเป็นแผนผังได้ดังนี้
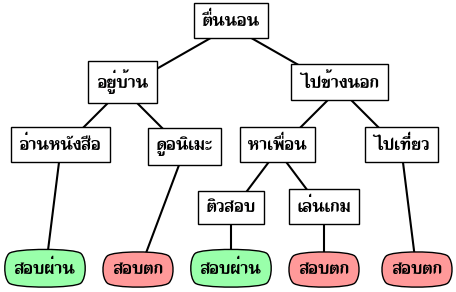
ลักษณะนี้เรียกว่าเป็นแผนผังต้นไม้ เพียงแต่ว่าปกติแล้วจะให้ด้านบนเป็นส่วนรากฐาน ในขณะที่ยิ่งงอกก็จะยิ่งลงไปข้างล่างเรื่อยๆ กลับทิศกลับต้นไม้ในโลกความเป็นจริง
วิธีการนี้ยังสามารถใช้กับข้อมูลที่เป็นตัวเลขได้โดยการตั้งเงื่อนไขเป็นมากหรือน้อยกว่า
เช่น ในการสอบวิชาหนึ่ง หากใครสอบกลางภาคได้ได้ 60 คะแนนขึ้นไป ปลายภาคได้ 40 ถือว่าสอบผ่าน แต่ถ้าไม่ได้ ต้องทำปลายภาคเกิน 70 จึงจะผ่าน
หากเขียนเป็นแผนผังจะได้ดังนี้
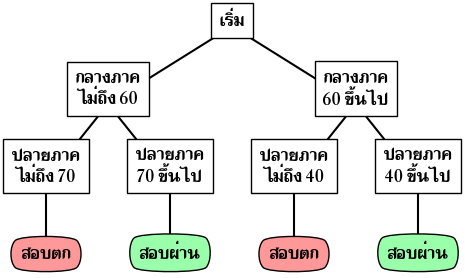
หากเขียนเป็นฟังก์ชันในไพธอนก็จะได้ในลักษณะแบบนี้
ในที่นี้ 1 คือสอบผ่าน 0 คือสอบไม่ผ่าน
อย่างไรก็ตาม หากต้องการหาคำตอบพร้อมกันหลายๆตัวใช้ numpy ช่วยอาจเขียนได้ดังนี้
ใครงงกับคำสั่ง where อ่านได้ใน https://phyblas.hinaboshi.com/numa19
ลองวาดเป็นแผนภาพแสดงอาณาเขตได้เป็นแบบนี้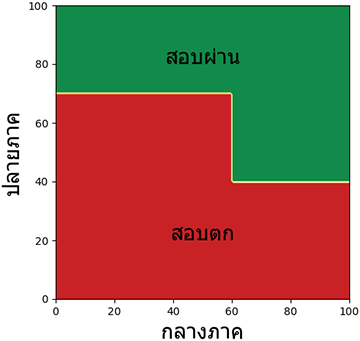
โดยอาศัยแนวคิดในลักษณะคล้ายๆกันนี้ เราสามารถนำมาประยุกต์ใช้เพื่อเขียนโปรแกรมสำหรับแบ่งข้อมูลออกเป็นกลุ่มโดยอาศัยเกณฑ์ต่างๆได้
ปัญหาที่ยกเมื่อครู่นี้ ลองสมมุติว่าถ้าอาจารย์ไม่ยอมบอกว่าเขาใช้เกณฑ์อะไรในการคิด แต่มีนักเรียนอยู่ทั้งหมด 50 คนมาสอบแล้วได้คะแนนเท่าไหร่ก็บันทึกไว้ แล้วก็ดูว่าใครได้คะแนนเท่าไหร่แล้วสอบผ่านหรือเปล่า
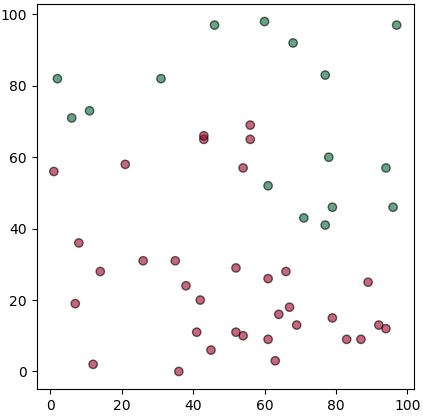
โค้ดสำหรับสร้างข้อมูลและวาดภาพนี้เขียนได้ดังนี้
ในที่นี้ x เป็นคะแนนสอบกลางภาค y เป็นคะแนนสอบปลายภาค และ z คือผลสอบว่าผ่านไม่ผ่าน (0=ไม่ผ่าน, 1=ผ่าน)
ที่จะวิเคราะห์ก็คือว่าจากข้อมูลที่มีอยู่ตรงนี้ จะสามารถบอกได้อย่างไรว่า วิชานี้มีเกณฑ์ในการตัดสินยังไง
นั่นก็คือ จะเขียนโปรแกรมยังไงให้สามารถขีดเส้นแบ่งออกมาเป็นอย่างในภาพแรกได้เองโดยที่เราไม่ต้องไปกำหนดค่าเองเลย
นี่เป็นวิธีคิดของการจำแนกประเภทข้อมูลโดยใช้ต้นไม้ตัดสินใจ
ที่จริงแล้วแนวทางการเขียนโปรแกรมสำหรับจำแนกประเภทข้อมูลนั้นมีอยู่หลายชนิด เช่นการวิเคราะห์การถดถอยโลจิสติก หรือวิธีการเพื่อนบ้านใกล้ที่สุด แต่ละวิธีการก็มีจุดเด่นจุดด้อยลักษณะเฉพาะต่างๆกันออกไป
สำหรับวิธีการต้นไม้ตัดสินใจนี้มีจุดเด่นอยู่ตรงที่ว่าจะพิจารณาตัวแปรทีละชนิดแล้วแบ่งซีกตามช่วงค่า ดังนั้นหากดูแผนภาพการแบ่งจะเห็นการแบ่งเป็นเส้นตรงตั้งฉากตลอด
โดยทั่วไปแล้วต้นไม้ตัดสินใจจะเป็นการแบ่งข้อมูลโดยแตกออกเป็นทีละ ๒ ส่วนไปเรื่อยๆ
ซึ่งจริงๆแล้วก็ไม่ใช่ว่าจะแตกเกิน ๒ ส่วนไม่ได้ แต่ว่าการแตกทีละ ๒ นั้นทำได้ง่าย ดังนั้นอัลกอริธึมส่วนใหญ่ที่ใช้แบ่งจึงมักจะเป็นการแบ่งทีละ ๒ ส่วน
แต่ละกิ่งก็อาจไม่จำเป็นต้องแบ่งเป็นจำนวนครั้งเท่ากัน กิ่งหนึ่งอาจไม่แบ่งต่อในขณะที่อีกกิ่งแบ่งต่อไปอีกยาวก็ได้

ลองค่อยๆคิดไปเป็นขั้นเป็นตอนดังนี้
เริ่มจากลองพิจารณาว่าถ้าเราอยากจะเริ่มแบ่งข้อมูลตามค่าแกน x เราอาจจะลองเอาค่า x ของแต่ละจุดมาเรียงแล้วคิดค่ากึ่งกลางที่แบ่งแต่ละจุด
อาจเขียนได้ในลักษณะนี้
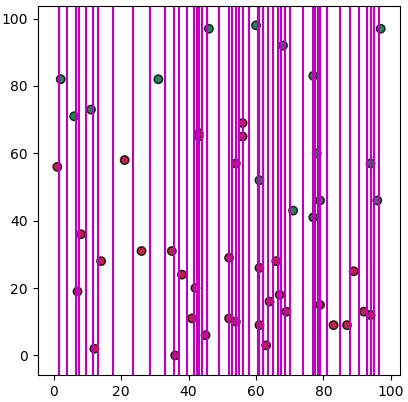
แต่ว่าเส้นที่กั้นแบ่งระหว่างชนิดเดียวกัน (สีเหมือนกัน) เราคงไม่ต้องการ ดังนั้นควรตัดออก เขียนได้ใหม่เป็นแบบนี้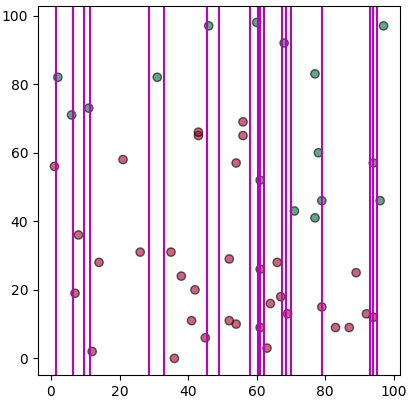
เท่านี้ก็เหลือแต่เส้นที่แบ่งระหว่างต่างสีกัน แต่ว่าก็ยังเยอะ ในจำนวนเส้นแบ่งมากมายนี้เราจะพิจารณายังไงว่าควรจะแบ่งตรงไหน?
หลักการที่นิยมใช้ก็คือ ดูว่าหลังจากแบ่งแล้วมีการปนกันของข้อมูลต่างชนิดแค่ไหน ยิ่งปะปนกันมากก็ยิ่งไม่ดี
ค่าที่แสดงว่ามีการปะปนกันมากแค่ไหนนั้นเรียกว่าค่าความไม่บริสุทธิ์ (纯度, impurity)
ค่าความไม่บริสุทธ์นั้นมีวิธีที่คิดอยู่หลายอย่าง ที่นิยมก็คือค่าเอนโทรปี (熵, entropy) และ ความไม่บริสุทธิ์ของจีนี (基尼不纯度, Gini impurity)
ค่าเอนโทรปีคำนวณได้ดังนี้
โดยที่ p(i|t) คือจำนวนสมาชิกกลุ่ม i ต่อจำนวนทั้งหมดในกิ่งนั้น
ส่วนค่าความไม่บริสุทธิ์ของจีนีคำนวณได้ดังนี้
ทั้งสองค่านี้มีลักษณะคล้ายกัน อย่างไรก็ตามค่าความไม่บริสุทธิ์ของจีนีเป็นที่นิยมใช้มากกว่า ครั้งนี้จึงจะใช้แค่ค่านี้เป็นหลัก
จากสูตรคำนวณ เราสามารถเขียนฟังก์ชันในไพธอนได้ดังนี้
โดย p ในที่นี้คืออาเรย์ p(i|t) ซึ่งก็คือสัดส่วนของแต่ละสมาชิก ซึ่งทั้งหมดรวมกันแล้วต้องเป็น 1
ความไม่บริสุทธิ์ยิ่งน้อยแสดงว่าการแบ่งยิ่งดี ดังนั้นเราลองให้วนซ้ำเพื่อหาดูว่าค่าแบ่งไหนทำให้ความไม่บริสุทธิ์รวมต่ำสุด จากนั้นก็แบ่งด้วยค่านั้น โดยความไม่บริสุทธิ์รวมนี้คิดดังนี้
ความไม่บริสุทธ์รวม = (ความไม่บริสุทธิฝั่งซ้าย×จำนวนฝั่งซ้าย + ความไม่บริสุทธิฝั่งขวา×จำนวนฝั่งขวา) / จำนวนทั้งหมด
ลองเขียนดูได้ดังนี้
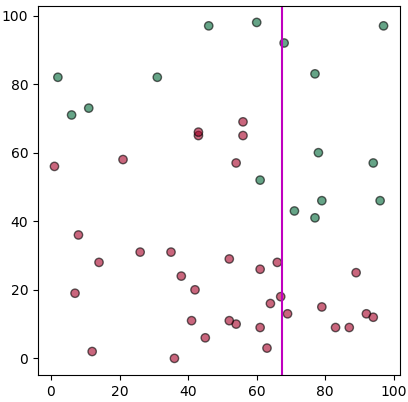
จะเห็นว่าได้เส้นแบ่งที่ดูเหมือนจะดีออกมา แม้ว่าจะยังต่างจากที่คาดหวังไว้สักหน่อย
ปัญหาอย่างหนึ่งก็คือในที่นี้เราคิดไปก่อนแล้วว่าจะแบ่งตามแกน x ก่อน แต่ในความเป็นจริงการแบ่งตามแกน x ก่อนนั้นดีสุดแล้วจริงหรือเปล่าก็ไม่รู้
ดังนั้นจึงควรจะพิจารณาตัวแปรทั้งหมดไปพร้อมๆกันแล้วดูว่าแบ่งแนวไหนให้ค่าความไม่บริสุทธิ์ต่ำกว่า
เขียนใหม่เป็นดังนี้
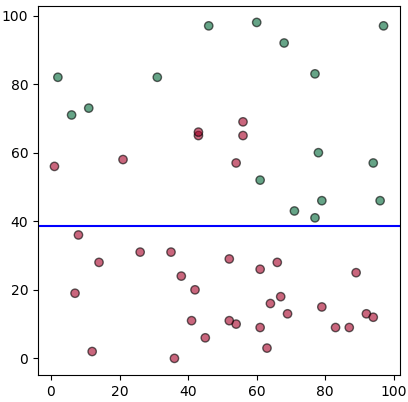
จะเห็นว่าพอทำแบบนี้แล้วพบว่าแบ่งตามแกน y ก่อนได้ผลดีกว่า เพราะว่าพอแบ่งแล้วส่วนด้านล่างกลายเป็นชนิดเดียวกันหมดเลย
เท่านี้การแบ่งครั้งแรกก็ทำได้สำเร็จแล้ว ต่อมาการจะแบ่งต่อก็ใช้วิธีการในทำนองเดียวกันกับข้อมูลที่แยกไว้แล้ว
เพื่อความสะดวกอาจลองเขียนออกมาเป็นรูปแบบของคลาส โดยจะเขียนคลาสของจุดแตกกิ่งขึ้นมา และจะสร้างออบเจ็กต์จุดแตกกิ่งออกมาทุกครั้งที่มีการแตกกิ่ง
การนำมาใช้งานก็ทำได้โดยเริ่มสร้างออบเจ็กต์ของจุดแยกขึ้นมา พอสร้างแล้วมันจะกลายเป็นเหมือนฟังก์ชันสำหรับคำนวนแบ่งหมวด โดยเรานิยามเมธอด __call__ ดังนั้นเวลาใช้ทำนายผลก็เรียกใช้เหมือนฟังก์ชันธรรมดา
ลองนำมาใช้ดูโดยเริ่มจากลองดูกรณีที่แยกแค่ครั้งเดียวก่อน นำมาใช้ทำนายแบ่งเขตโดยใช้ contourf ก็จะเขียนแบบนี้
พอจะนำมาแตกต่อก็เขียนได้แบบนี้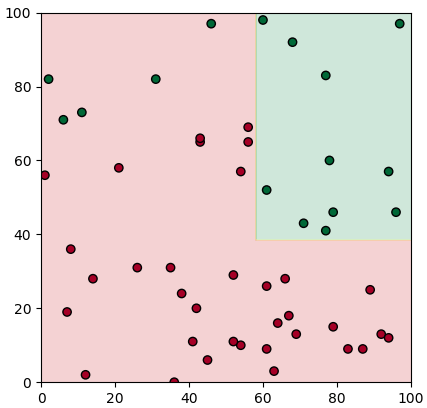
จะเห็นว่าส่วนด้านล่างไม่สามารถแตกต่อได้แล้วจึงหยุดแค่นี้ แต่ว่าด้านบนจะมีการแยก
ด้านบนแยกแล้วก็ยังมีส่วนที่ยังปนจำเป็นต้องแยกอยู่อีก ดังนั้นจึงยังต้องแตกเงื่อนไขต่อไป
แต่ว่า หากทำแบบนี้ไปเรื่อยๆละก็คงต้องเขียนไม่รู้จบ ดังนั้นจริงๆแล้ววิธีการเขียนแบบนี้จึงยังไม่เหมาะต่อการใช้งานจริงอยู่
เราจะพัฒนาแนวคิดต่อไป โดยคราวนี้ทำคลาสจุดแตกให้ออกมาเป็นรูปแบบที่พอสร้างขึ้นมาก็สามารถแตกกิ่งก้านออกไปเองได้ และตัดสินเอาเองว่าควรแตกต่อหรือไม่โดยดูจากว่าในกิ่งนั้นๆมีการแบ่งโดยสมบูรณ์หรือยัง
อาจสามารถเขียนใหม่ได้แบบนี้
จะเห็นว่าที่ต่างจากเดิมชัดเจนคือตอนท้ายสุดของตอนสร้างกิ่งจะมีการสร้างกิ่งย่อยขึ้นมาเองเลย
ต่อไปก็ลองนำมาใช้กับข้อมูลเดิม เวลาใช้ก็เขียนแค่นี้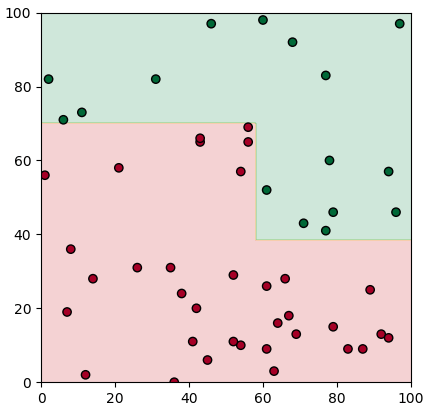
แค่สร้างจุดแตกอันแรก ซึ่งในที่นี้เรียกว่าเป็นราก มันก็จะแตกกิ่งออกต่อเอง
ตัวเลข 3 ที่เป็นอาร์กิวเมนต์ตัวสุดท้ายจะเป็นจำนวนชั้นของการแตกกิ่ง ในที่นี้ต้องการให้แตก ๓ ครั้งจึงใส่ 3 แต่ในตัวอย่างนี้ต่อให้ใส่เยอะกว่านั้นก็ไม่มีการแบ่งต่อแล้วเพราะถูกแบ่งโดยสมบูรณ์แล้ว
สุดท้ายก็เรียกใช้เพื่อทำนาย เท่านี้ก็เรียบร้อย
เพื่อให้ดูแล้วเข้าใจง่ายขึ้นเราอาจลองสร้างคลาสใหม่ขึ้นมาเพื่อห่อหุ้ม นั่นคือคลาสของต้นไม้ตัดสินใจ
ลักษณะที่ทำขึ้นมานี้จะเป็นรูปแบบในทำนองเดียวกันกับคลาสของการถดถอยโลจิสติก (https://phyblas.hinaboshi.com/20171006) และวิธีการเพื่อนบ้านใกล้สุด (https://phyblas.hinaboshi.com/20171028) ซึ่งเคยสร้างมาก่อนหน้านี้
นั่นคือมีเมธอด rianru ไว้ใช้สำหรับนำข้อมูลมาเรียนรู้ และมีเมธอด thamnai ในการทำนายผล
สำหรับกรณีของต้นไม้ตัดสินใจ เมื่อใช้เมธอดเรียนรู้ก็จะเห็นการสร้างจุดแตกแรก ซึ่งก็คือรากขึ้นมา และจะเกิดการแตกกิ่งก้านออกมา
ตอนสร้างต้องกำหนดค่าความลึก (luek) คือจำนวนครั้งสูงสุดที่จะแตกกิ่ง
ลองนำมาใช้ดู คราวนี้ลองสุ่มสร้างข้อมูลใหม่มาใช้ดูบ้าง โดยใช้ข้อมูลเป็นกลุ่มก้อนซึ่งสร้างด้วย make_blobs (https://phyblas.hinaboshi.com/20161127) ลองให้ทำการแตกกิ่งไปเรื่อยๆจนกว่าจะแบ่งได้หมด คือใส่ค่าจำนวนการแตกสูงสุดเป็นค่าเยอะๆไว้
พอดูจากผลที่ได้ตรงนี้จะเห็นลักษณะเด่นของการแบ่งด้วยต้นไม้ตัดสินใจได้ชัดเจน นั่นคือข้อมูลที่ซ้อนกันอาจถูกแบ่งเป็นก้อนๆแบบนี้
ลักษณะแบบนี้ทำให้เกิดการเรียนรู้เกินได้ง่าย คือแบบจำลองจะถูกปรับให้เข้ากับข้อมูลที่ใส่ลงไปนี้อย่างเต็มที่ แต่ซับซ้อนเกินไปจนอาจไม่สามารถใช้ทำนายข้อมูลทั่วไปได้
เพื่อไม่ให้เป็นแบบนี้อาจลดจำนวนความลึกในการแตกลง เช่นลองให้เหลือ 5
แบบนี้จะเห็นว่าการแบ่งถูกทำแค่พอประมาณ ไม่ละเอียดจนเกินไป
ในตัวอย่างที่ผ่านมาเราทำการแบ่งแค่ ๒ กลุ่ม แต่หากจะลองนำมาแบ่งเป็นหลายกลุ่มก็แน่นอนว่าทำได้เช่นกัน ลองดูได้เช่น
สุดท้าย ขอลองสร้างเป็นภาพต้นไม้ขึ้นเพื่อเปรียบเทียบ ให้เห็นถึงภาพการแตกกิ่งของต้นไม้
สมมุติว่าต้นไม้แต่ละต้นคือข้อมูลชุดหนึ่งที่ต้องการแบ่งเป็น ๒ กลุ่ม เมื่อลองแตกกิ่งครั้งนึงเป็น ๒ ส่วนจะได้เป็นแบบนี้ พุ่มใบที่อยู่ตรงปลายยอดจะมีสีต่างกัน แสดงด้วยสีของกลุ่มที่มีจำนวนมากที่สุดในกิ่งนั้น ความกว้างของพุ่มใบแสดงถึงจำนวนข้อมูล

ถ้าแตกต่อเป็นรอบที่ ๒ แต่ละกิ่งก็จะย่อยลงไปอีก แต่จะเห็นได้ว่าบางกิ่งไม่ถูกแตกต่อแล้ว

แล้วก็แตกต่อไปอีกเป็นรอบที่ ๓, ๔ และ ๕ ก็จะเป็นแบบนี้



โดยสรุป ข้อดีและข้อเสียของวิธีการต้นไม้ตัดสินใจ
ข้อดี
- มองแล้วเข้าใจได้ง่าย ดูลำดับขั้นตอนการตัดสินใจแล้ววิเคราะห์ได้
- ไม่ขึ้นกับการกระจายตัวของข้อมูล ไม่จำเป็นต้องทำข้อมูลให้เป็นมาตรฐานก่อน
- จัดการแยกข้อมูลที่มีลักษณะเป็นเกาะลอยได้ดี
ข้อเสีย
- อาจแตกกิ่งมากไปทำให้เกิดการเรียนรู้เกินได้ง่าย
- หากข้อมูลเปลี่ยนแปลงแค่นิดเดียวผลการแตกกิ่งอาจเปลี่ยนไปคนละเรื่องเลยได้
- ไม่เหมาะกับข้อมูลที่มีลักษณะเป็นเชิงเส้น
- การแบ่งพิจารณาตัวแปรทีละตัวแยกกันตลอด ไม่สามารถใช้ตัวแปรสองชนิดขึ้นไปเป็นเกณฑ์ในการแบ่งพร้อมกันได้
วิธีการต้นไม้ตัดสินใจนั้นจริงๆแล้วมีรายละเอียดปลีกย่อยอะไรอีกมาก ซึ่งก็คงจะไม่ขอลงลึกแล้ว ในที่นี้แค่ต้องการเขียนแนวคิดคร่าวๆและพื้นฐานวิธีการสร้าง
หากต้องการใช้งานจริงๆอาจใช้ sklearn ซึ่งถูกเขียนมาอย่างดี สามารถปรับแต่งอะไรได้มากมาย เกี่ยวกับการใช้สามารถอ่านได้ใน https://phyblas.hinaboshi.com/20171108
อ้างอิง
ชีวิตคนเรามักจะเผชิญกับทางเลือกอยู่เสมอ แล้วการเลือกนั้นก็อาจมีผลสำคัญทำให้เกิดผลลงเอยต่างกันออกไป
ยกตัวอย่างเช่น เราเลือกว่าจะอยู่บ้านหรือออกไปข้างนอก อยู่บ้านจะอ่านหนังสือหรือเล่นเกม ออกไปข้างนอกแล้วไปเจอเพื่อนหรือเปล่า เจอเพื่อนแล้วจะชวนกันไปเล่นเกมหรือไปอ่านหนังสือ แล้วสุดท้ายการกระทำเหล่านั้นจะเป็นตัวตัดสินว่าเราจะสอบปลายภาคผ่านหรือเปล่า
อาจเขียนแจกแจงเป็นแผนผังได้ดังนี้

ลักษณะนี้เรียกว่าเป็นแผนผังต้นไม้ เพียงแต่ว่าปกติแล้วจะให้ด้านบนเป็นส่วนรากฐาน ในขณะที่ยิ่งงอกก็จะยิ่งลงไปข้างล่างเรื่อยๆ กลับทิศกลับต้นไม้ในโลกความเป็นจริง
วิธีการนี้ยังสามารถใช้กับข้อมูลที่เป็นตัวเลขได้โดยการตั้งเงื่อนไขเป็นมากหรือน้อยกว่า
เช่น ในการสอบวิชาหนึ่ง หากใครสอบกลางภาคได้ได้ 60 คะแนนขึ้นไป ปลายภาคได้ 40 ถือว่าสอบผ่าน แต่ถ้าไม่ได้ ต้องทำปลายภาคเกิน 70 จึงจะผ่าน
หากเขียนเป็นแผนผังจะได้ดังนี้

หากเขียนเป็นฟังก์ชันในไพธอนก็จะได้ในลักษณะแบบนี้
def phonsop(klangphak,plaiphak):
if(klangphak>60):
if(plaiphak>40):
return 1
else:
return 0
else:
if(plaiphak>70):
return 1
else:
return 0ในที่นี้ 1 คือสอบผ่าน 0 คือสอบไม่ผ่าน
อย่างไรก็ตาม หากต้องการหาคำตอบพร้อมกันหลายๆตัวใช้ numpy ช่วยอาจเขียนได้ดังนี้
import numpy as np
def phonsop(klangphak,plaiphak):
return np.where(klangphak>60,plaiphak>40,plaiphak>70)ใครงงกับคำสั่ง where อ่านได้ใน https://phyblas.hinaboshi.com/numa19
ลองวาดเป็นแผนภาพแสดงอาณาเขตได้เป็นแบบนี้
import matplotlib.pyplot as plt
nmesh = 100
mx,my = np.meshgrid(np.linspace(0,100,nmesh),np.linspace(0,100,nmesh))
mz = phonsop(mx,my)
plt.figure(figsize=[6,5])
plt.axes(aspect=1)
plt.xlabel(u'กลางภาค',family='Tahoma',size=20)
plt.ylabel(u'ปลายภาค',family='Tahoma',size=20)
plt.contourf(mx,my,mz,cmap='RdYlGn')
plt.text(50,80,u'สอบผ่าน',family='Tahoma',size=20,ha='center')
plt.text(50,20,u'สอบตก',family='Tahoma',size=20,ha='center')
plt.show()
โดยอาศัยแนวคิดในลักษณะคล้ายๆกันนี้ เราสามารถนำมาประยุกต์ใช้เพื่อเขียนโปรแกรมสำหรับแบ่งข้อมูลออกเป็นกลุ่มโดยอาศัยเกณฑ์ต่างๆได้
ปัญหาที่ยกเมื่อครู่นี้ ลองสมมุติว่าถ้าอาจารย์ไม่ยอมบอกว่าเขาใช้เกณฑ์อะไรในการคิด แต่มีนักเรียนอยู่ทั้งหมด 50 คนมาสอบแล้วได้คะแนนเท่าไหร่ก็บันทึกไว้ แล้วก็ดูว่าใครได้คะแนนเท่าไหร่แล้วสอบผ่านหรือเปล่า

โค้ดสำหรับสร้างข้อมูลและวาดภาพนี้เขียนได้ดังนี้
x = np.array([54,71,60,54,42,64,43,89,96,38,79,52,56,92,7,8,2,83,77,87,97,79,46,78,11,63,14,94,52,41,26,77,45,56,1,61,61,61,94,68,35,43,69,6,66,67,21,12,31,36])
y = np.array([57,43,98,10,20,16,65,25,46,24,15,11,65,13,19,36,82,9,83,9,97,46,97,60,73,3,28,12,29,11,31,41,6,69,56,26,52,9,57,92,31,66,13,71,28,18,58,2,82,0])
z = np.array([0,1,1,0,0,0,0,0,1,0,0,0,0,0,0,0,1,0,1,0,1,1,1,1,1,0,0,0,0,0,0,1,0,0,0,0,1,0,1,1,0,0,0,1,0,0,0,0,1,0])
plt.axes(aspect=1)
plt.scatter(x,y,c=z,alpha=0.6,edgecolor='k',cmap='RdYlGn')
plt.show()ในที่นี้ x เป็นคะแนนสอบกลางภาค y เป็นคะแนนสอบปลายภาค และ z คือผลสอบว่าผ่านไม่ผ่าน (0=ไม่ผ่าน, 1=ผ่าน)
ที่จะวิเคราะห์ก็คือว่าจากข้อมูลที่มีอยู่ตรงนี้ จะสามารถบอกได้อย่างไรว่า วิชานี้มีเกณฑ์ในการตัดสินยังไง
นั่นก็คือ จะเขียนโปรแกรมยังไงให้สามารถขีดเส้นแบ่งออกมาเป็นอย่างในภาพแรกได้เองโดยที่เราไม่ต้องไปกำหนดค่าเองเลย
นี่เป็นวิธีคิดของการจำแนกประเภทข้อมูลโดยใช้ต้นไม้ตัดสินใจ
ที่จริงแล้วแนวทางการเขียนโปรแกรมสำหรับจำแนกประเภทข้อมูลนั้นมีอยู่หลายชนิด เช่นการวิเคราะห์การถดถอยโลจิสติก หรือวิธีการเพื่อนบ้านใกล้ที่สุด แต่ละวิธีการก็มีจุดเด่นจุดด้อยลักษณะเฉพาะต่างๆกันออกไป
สำหรับวิธีการต้นไม้ตัดสินใจนี้มีจุดเด่นอยู่ตรงที่ว่าจะพิจารณาตัวแปรทีละชนิดแล้วแบ่งซีกตามช่วงค่า ดังนั้นหากดูแผนภาพการแบ่งจะเห็นการแบ่งเป็นเส้นตรงตั้งฉากตลอด
โดยทั่วไปแล้วต้นไม้ตัดสินใจจะเป็นการแบ่งข้อมูลโดยแตกออกเป็นทีละ ๒ ส่วนไปเรื่อยๆ
ซึ่งจริงๆแล้วก็ไม่ใช่ว่าจะแตกเกิน ๒ ส่วนไม่ได้ แต่ว่าการแตกทีละ ๒ นั้นทำได้ง่าย ดังนั้นอัลกอริธึมส่วนใหญ่ที่ใช้แบ่งจึงมักจะเป็นการแบ่งทีละ ๒ ส่วน
แต่ละกิ่งก็อาจไม่จำเป็นต้องแบ่งเป็นจำนวนครั้งเท่ากัน กิ่งหนึ่งอาจไม่แบ่งต่อในขณะที่อีกกิ่งแบ่งต่อไปอีกยาวก็ได้

ลองค่อยๆคิดไปเป็นขั้นเป็นตอนดังนี้
เริ่มจากลองพิจารณาว่าถ้าเราอยากจะเริ่มแบ่งข้อมูลตามค่าแกน x เราอาจจะลองเอาค่า x ของแต่ละจุดมาเรียงแล้วคิดค่ากึ่งกลางที่แบ่งแต่ละจุด
อาจเขียนได้ในลักษณะนี้
x_riang = np.sort(x)
x_kan = (x_riang[1:]+x_riang[:-1])/2
plt.axes(aspect=1)
plt.scatter(x,y,c=z,edgecolor='k',alpha=0.6,cmap='RdYlGn')
for khabaeng in x_kan:
plt.axvline(khabaeng,color='m')
plt.show()
แต่ว่าเส้นที่กั้นแบ่งระหว่างชนิดเดียวกัน (สีเหมือนกัน) เราคงไม่ต้องการ ดังนั้นควรตัดออก เขียนได้ใหม่เป็นแบบนี้
xas = x.argsort()
x_riang = x[xas]
z_riang = z[xas]
x_kan = (x_riang[1:]+x_riang[:-1])/2
x_kan = x_kan[z_riang[1:]!=z_riang[:-1]]
plt.axes(aspect=1)
plt.scatter(x,y,c=z,edgecolor='k',alpha=0.6,cmap='RdYlGn')
for khabaeng in x_kan:
plt.axvline(khabaeng,color='m')
plt.show()
เท่านี้ก็เหลือแต่เส้นที่แบ่งระหว่างต่างสีกัน แต่ว่าก็ยังเยอะ ในจำนวนเส้นแบ่งมากมายนี้เราจะพิจารณายังไงว่าควรจะแบ่งตรงไหน?
หลักการที่นิยมใช้ก็คือ ดูว่าหลังจากแบ่งแล้วมีการปนกันของข้อมูลต่างชนิดแค่ไหน ยิ่งปะปนกันมากก็ยิ่งไม่ดี
ค่าที่แสดงว่ามีการปะปนกันมากแค่ไหนนั้นเรียกว่าค่าความไม่บริสุทธิ์ (纯度, impurity)
ค่าความไม่บริสุทธ์นั้นมีวิธีที่คิดอยู่หลายอย่าง ที่นิยมก็คือค่าเอนโทรปี (熵, entropy) และ ความไม่บริสุทธิ์ของจีนี (基尼不纯度, Gini impurity)
ค่าเอนโทรปีคำนวณได้ดังนี้
โดยที่ p(i|t) คือจำนวนสมาชิกกลุ่ม i ต่อจำนวนทั้งหมดในกิ่งนั้น
ส่วนค่าความไม่บริสุทธิ์ของจีนีคำนวณได้ดังนี้
ทั้งสองค่านี้มีลักษณะคล้ายกัน อย่างไรก็ตามค่าความไม่บริสุทธิ์ของจีนีเป็นที่นิยมใช้มากกว่า ครั้งนี้จึงจะใช้แค่ค่านี้เป็นหลัก
จากสูตรคำนวณ เราสามารถเขียนฟังก์ชันในไพธอนได้ดังนี้
def gini(p):
return 1-(p**2).sum()โดย p ในที่นี้คืออาเรย์ p(i|t) ซึ่งก็คือสัดส่วนของแต่ละสมาชิก ซึ่งทั้งหมดรวมกันแล้วต้องเป็น 1
ความไม่บริสุทธิ์ยิ่งน้อยแสดงว่าการแบ่งยิ่งดี ดังนั้นเราลองให้วนซ้ำเพื่อหาดูว่าค่าแบ่งไหนทำให้ความไม่บริสุทธิ์รวมต่ำสุด จากนั้นก็แบ่งด้วยค่านั้น โดยความไม่บริสุทธิ์รวมนี้คิดดังนี้
ความไม่บริสุทธ์รวม = (ความไม่บริสุทธิฝั่งซ้าย×จำนวนฝั่งซ้าย + ความไม่บริสุทธิฝั่งขวา×จำนวนฝั่งขวา) / จำนวนทั้งหมด
ลองเขียนดูได้ดังนี้
n = len(z)
gn_noisut = 1
for khabaeng in x_kan:
baeng = khabaeng>x
z_sai = z[baeng]
z_khwa = z[~baeng]
n_sai = float(len(z_sai))
n_khwa = float(len(z_khwa))
gn = (gini(np.bincount(z_sai)/n_sai)*n_sai+gini(np.bincount(z_khwa)/n_khwa)*n_khwa)/n
if(gn_noisut>gn):
gn_noisut = gn
khabaeng_disut = khabaeng
plt.axes(aspect=1)
plt.scatter(x,y,c=z,edgecolor='k',alpha=0.6,cmap='RdYlGn')
plt.axvline(khabaeng_disut,color='m')
plt.show()
จะเห็นว่าได้เส้นแบ่งที่ดูเหมือนจะดีออกมา แม้ว่าจะยังต่างจากที่คาดหวังไว้สักหน่อย
ปัญหาอย่างหนึ่งก็คือในที่นี้เราคิดไปก่อนแล้วว่าจะแบ่งตามแกน x ก่อน แต่ในความเป็นจริงการแบ่งตามแกน x ก่อนนั้นดีสุดแล้วจริงหรือเปล่าก็ไม่รู้
ดังนั้นจึงควรจะพิจารณาตัวแปรทั้งหมดไปพร้อมๆกันแล้วดูว่าแบ่งแนวไหนให้ค่าความไม่บริสุทธิ์ต่ำกว่า
เขียนใหม่เป็นดังนี้
X = np.stack([x,y],1) # นำมารวมกันเป็นอาเรย์สองมิติอันเดียว
n = len(z)
gn_noisut = 1
for j in range(X.shape[1]):
xas = X[:,j].argsort()
x_riang = X[:,j][xas]
z_riang = z[xas]
x_kan = (x_riang[1:]+x_riang[:-1])/2
x_kan = x_kan[z_riang[1:]!=z_riang[:-1]]
for khabaeng in x_kan:
baeng = khabaeng>X[:,j]
z_sai = z[baeng]
z_khwa = z[~baeng]
n_sai = float(len(z_sai))
n_khwa = float(len(z_khwa))
gn = (gini(np.bincount(z_sai)/n_sai)*n_sai+gini(np.bincount(z_khwa)/n_khwa)*n_khwa)/n
if(gn_noisut>gn):
gn_noisut = gn
j_disut = j
khabaeng_disut = khabaeng
plt.axes(aspect=1)
plt.scatter(x,y,c=z,edgecolor='k',alpha=0.6,cmap='RdYlGn')
if(j_disut==0):
plt.axvline(khabaeng_disut,color='m')
else:
plt.axhline(khabaeng_disut,color='b')
plt.show()
จะเห็นว่าพอทำแบบนี้แล้วพบว่าแบ่งตามแกน y ก่อนได้ผลดีกว่า เพราะว่าพอแบ่งแล้วส่วนด้านล่างกลายเป็นชนิดเดียวกันหมดเลย
เท่านี้การแบ่งครั้งแรกก็ทำได้สำเร็จแล้ว ต่อมาการจะแบ่งต่อก็ใช้วิธีการในทำนองเดียวกันกับข้อมูลที่แยกไว้แล้ว
เพื่อความสะดวกอาจลองเขียนออกมาเป็นรูปแบบของคลาส โดยจะเขียนคลาสของจุดแตกกิ่งขึ้นมา และจะสร้างออบเจ็กต์จุดแตกกิ่งออกมาทุกครั้งที่มีการแตกกิ่ง
class Chuttaek:
def __init__(self,X,z):
n = len(z)
if(len(np.unique(z))==1): # กรณีที่สมาชิกเหมือนกันทั้งหมด ไม่ต้องแบ่งแล้ว
self.khabaeng = np.inf
self.saipen = z[0]
self.j = 0
else: # กรณีที่สมาชิกมีการปนกันอยู่ ให้ทำการแบ่ง
self.gn = 1
for j in range(X.shape[1]):
x = X[:,j]
xas = x.argsort()
x_riang = x[xas]
z_riang = z[xas]
x_kan = (x_riang[1:]+x_riang[:-1])/2
x_kan = x_kan[z_riang[1:]!=z_riang[:-1]]
for khabaeng in x_kan:
baeng = khabaeng>x
z_sai = z[baeng]
z_khwa = z[~baeng]
n_sai = float(len(z_sai))
n_khwa = float(len(z_khwa))
gn = (gini(np.bincount(z_sai)/n_sai)*n_sai+gini(np.bincount(z_khwa)/n_khwa)*n_khwa)/n
if(self.gn>gn):
self.gn = gn
self.j = j
self.khabaeng = khabaeng
self.saipen = (baeng==z).mean()>0.5
def __call__(self,X):
return (X[:,self.j]<self.khabaeng)==self.saipenการนำมาใช้งานก็ทำได้โดยเริ่มสร้างออบเจ็กต์ของจุดแยกขึ้นมา พอสร้างแล้วมันจะกลายเป็นเหมือนฟังก์ชันสำหรับคำนวนแบ่งหมวด โดยเรานิยามเมธอด __call__ ดังนั้นเวลาใช้ทำนายผลก็เรียกใช้เหมือนฟังก์ชันธรรมดา
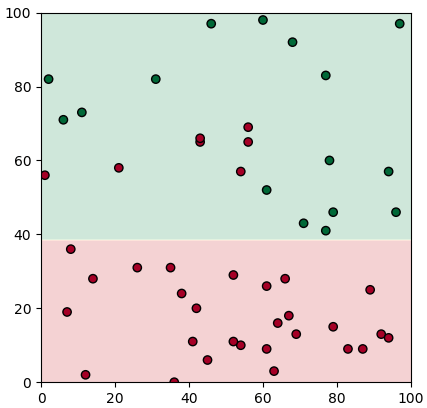
ลองนำมาใช้ดูโดยเริ่มจากลองดูกรณีที่แยกแค่ครั้งเดียวก่อน นำมาใช้ทำนายแบ่งเขตโดยใช้ contourf ก็จะเขียนแบบนี้
nmesh = 200
mx,my = np.meshgrid(np.linspace(0,100,nmesh),np.linspace(0,100,nmesh))
mX = np.stack([mx,my],1)
ct = Chuttaek(X,z) # สร้างจุดแตกกิ่ง
mz = ct(mX) # ทำนายผล
# วาด
def plottare(X,z,mx,my,mz):
plt.figure()
plt.axes(aspect=1,xlim=[0,100],ylim=[0,100])
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='RdYlGn',vmin=0,vmax=1)
plt.contourf(mx,my,mz,alpha=0.2,cmap='RdYlGn',zorder=0)
plt.show()
plottare(X,z,mx,my,mz)
พอจะนำมาแตกต่อก็เขียนได้แบบนี้
o = ct(X)
ct1 = Chuttaek(X[o],z[o])
ct2 = Chuttaek(X[~o],z[~o])
mz = np.where(ct(mX),ct1(mX),ct2(mX))
plottare(X,z,mx,my,mz)
จะเห็นว่าส่วนด้านล่างไม่สามารถแตกต่อได้แล้วจึงหยุดแค่นี้ แต่ว่าด้านบนจะมีการแยก
ด้านบนแยกแล้วก็ยังมีส่วนที่ยังปนจำเป็นต้องแยกอยู่อีก ดังนั้นจึงยังต้องแตกเงื่อนไขต่อไป
แต่ว่า หากทำแบบนี้ไปเรื่อยๆละก็คงต้องเขียนไม่รู้จบ ดังนั้นจริงๆแล้ววิธีการเขียนแบบนี้จึงยังไม่เหมาะต่อการใช้งานจริงอยู่
เราจะพัฒนาแนวคิดต่อไป โดยคราวนี้ทำคลาสจุดแตกให้ออกมาเป็นรูปแบบที่พอสร้างขึ้นมาก็สามารถแตกกิ่งก้านออกไปเองได้ และตัดสินเอาเองว่าควรแตกต่อหรือไม่โดยดูจากว่าในกิ่งนั้นๆมีการแบ่งโดยสมบูรณ์หรือยัง
อาจสามารถเขียนใหม่ได้แบบนี้
class Chuttaek:
def __init__(self,X,z,chan):
self.chan = chan # ชั้นของจุดแตกกิ่ง
self.n = len(z) # จำนวนข้อมูลในกิ่งนี้
self.king = []
if(len(np.unique(z))==1): # หากสมาชิกเป็นชนิดเดียวกันหมดก็ไม่ต้องแตกกิ่งแล้ว
self.z = z[0] # เก็บค่าคำตอบของส่วนนั้น
elif(chan==0): # หากจำนวนชั้นเหลือเป็น 0 แล้วก็ไม่ต้องแตกแล้วเช่นกัน
self.z = np.bincount(z).argmax() # ใช้ค่าที่มีมากที่สุดเป็นคำตอบของส่วนนั้น
else:
self.gn = 1 # ค่าความไม่บริสุทธิ์ของจีนีตั้งต้น
for j in range(X.shape[1]): # วนเปลี่ยนตัวแปรต้นที่พิจารณา
x = X[:,j]
xas = x.argsort()
x_riang = x[xas]
z_riang = z[xas]
x_kan = (x_riang[1:]+x_riang[:-1])/2
x_kan = x_kan[z_riang[1:]!=z_riang[:-1]]
for khabaeng in x_kan:
baeng = khabaeng>x
z_sai = z[baeng]
z_khwa = z[~baeng]
n_sai = float(len(z_sai))
n_khwa = float(len(z_khwa))
gn = (gini(np.bincount(z_sai)/n_sai)*n_sai+gini(np.bincount(z_khwa)/n_khwa)*n_khwa)/self.n
if(self.gn>gn): # ถ้าเจอค่าจีนีที่ต่ำกว่าเดิมก็เก็บค่าใหม่นั้นพร้อมทั้งบันทึกตัวแปรที่ใช้แบ่งและค่าที่แบ่ง
self.gn = gn # ค่าจีนีต่ำสุด
self.j = j # ดัชนีของตัวแปรที่ใช้แบ่ง
self.khabaeng = khabaeng # ค่าที่ใช้แบ่ง
o = (self.khabaeng>X[:,self.j]) # แบ่งข้อมูลเพื่อแตกกิ่งต่อไป
self.king = [Chuttaek(X[o],z[o],chan-1),Chuttaek(X[~o],z[~o],chan-1)]
def __call__(self,X):
if(self.king==[]): # ถ้าไม่มีกิ่งแล้วก็ให้คำตอบเดียวเป็นค่าของส่วนนั้นเลย
return self.z
else: # ถ้ามีกิ่งก็ให้ทำการแยกกรณีไล่เรียกกิ่งย่อยต่อไป
o = self.khabaeng>X[:,self.j]
return np.where(o,self.king[0](X),self.king[1](X))จะเห็นว่าที่ต่างจากเดิมชัดเจนคือตอนท้ายสุดของตอนสร้างกิ่งจะมีการสร้างกิ่งย่อยขึ้นมาเองเลย
ต่อไปก็ลองนำมาใช้กับข้อมูลเดิม เวลาใช้ก็เขียนแค่นี้
rak = Chuttaek(X,z,3)
mz = rak(mX)
plottare(X,z,mx,my,mz)
แค่สร้างจุดแตกอันแรก ซึ่งในที่นี้เรียกว่าเป็นราก มันก็จะแตกกิ่งออกต่อเอง
ตัวเลข 3 ที่เป็นอาร์กิวเมนต์ตัวสุดท้ายจะเป็นจำนวนชั้นของการแตกกิ่ง ในที่นี้ต้องการให้แตก ๓ ครั้งจึงใส่ 3 แต่ในตัวอย่างนี้ต่อให้ใส่เยอะกว่านั้นก็ไม่มีการแบ่งต่อแล้วเพราะถูกแบ่งโดยสมบูรณ์แล้ว
สุดท้ายก็เรียกใช้เพื่อทำนาย เท่านี้ก็เรียบร้อย
เพื่อให้ดูแล้วเข้าใจง่ายขึ้นเราอาจลองสร้างคลาสใหม่ขึ้นมาเพื่อห่อหุ้ม นั่นคือคลาสของต้นไม้ตัดสินใจ
class TonmaiTatsinchai:
def __init__(self,luek):
self.luek = luek
def rianru(self,X,z):
self.rak = Chuttaek(X,z,self.luek)
def thamnai(self,X):
return self.rak(X)ลักษณะที่ทำขึ้นมานี้จะเป็นรูปแบบในทำนองเดียวกันกับคลาสของการถดถอยโลจิสติก (https://phyblas.hinaboshi.com/20171006) และวิธีการเพื่อนบ้านใกล้สุด (https://phyblas.hinaboshi.com/20171028) ซึ่งเคยสร้างมาก่อนหน้านี้
นั่นคือมีเมธอด rianru ไว้ใช้สำหรับนำข้อมูลมาเรียนรู้ และมีเมธอด thamnai ในการทำนายผล
สำหรับกรณีของต้นไม้ตัดสินใจ เมื่อใช้เมธอดเรียนรู้ก็จะเห็นการสร้างจุดแตกแรก ซึ่งก็คือรากขึ้นมา และจะเกิดการแตกกิ่งก้านออกมา
ตอนสร้างต้องกำหนดค่าความลึก (luek) คือจำนวนครั้งสูงสุดที่จะแตกกิ่ง
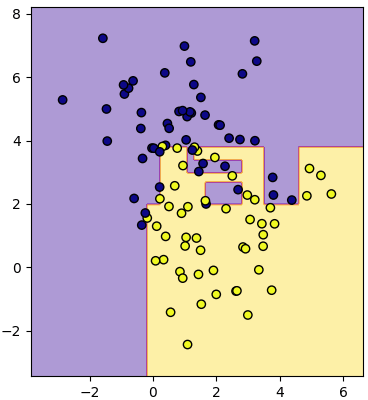
ลองนำมาใช้ดู คราวนี้ลองสุ่มสร้างข้อมูลใหม่มาใช้ดูบ้าง โดยใช้ข้อมูลเป็นกลุ่มก้อนซึ่งสร้างด้วย make_blobs (https://phyblas.hinaboshi.com/20161127) ลองให้ทำการแตกกิ่งไปเรื่อยๆจนกว่าจะแบ่งได้หมด คือใส่ค่าจำนวนการแตกสูงสุดเป็นค่าเยอะๆไว้
from sklearn import datasets
X,z = datasets.make_blobs(n_samples=100,n_features=2,centers=2,cluster_std=1.5,random_state=0)
tt = TonmaiTatsinchai(100)
tt.rianru(X,z)
nmesh = 200
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,nmesh),np.linspace(X[:,1].min()-1,X[:,1].max()+1,nmesh))
mX = np.stack([mx,my],1)
mz = tt.thamnai(mX)
def plottiamo(X,z,mx,my,mz):
plt.figure()
plt.axes(aspect=1)
plt.scatter(X[:,0],X[:,1],c=z,edgecolor='k',cmap='plasma')
plt.contourf(mx,my,mz,alpha=0.4,cmap='plasma',zorder=0)
plt.show()
plottiamo(X,z,mx,my,mz)
พอดูจากผลที่ได้ตรงนี้จะเห็นลักษณะเด่นของการแบ่งด้วยต้นไม้ตัดสินใจได้ชัดเจน นั่นคือข้อมูลที่ซ้อนกันอาจถูกแบ่งเป็นก้อนๆแบบนี้
ลักษณะแบบนี้ทำให้เกิดการเรียนรู้เกินได้ง่าย คือแบบจำลองจะถูกปรับให้เข้ากับข้อมูลที่ใส่ลงไปนี้อย่างเต็มที่ แต่ซับซ้อนเกินไปจนอาจไม่สามารถใช้ทำนายข้อมูลทั่วไปได้
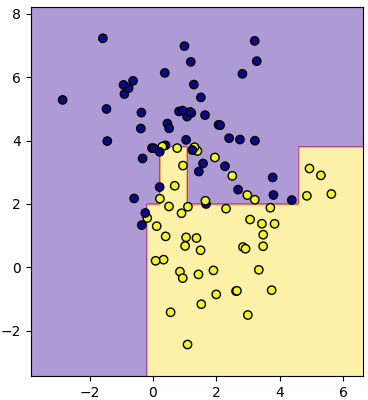
เพื่อไม่ให้เป็นแบบนี้อาจลดจำนวนความลึกในการแตกลง เช่นลองให้เหลือ 5
tt = TonmaiTatsinchai(5)
tt.rianru(X,z)
mz = tt.thamnai(mX)
plottiamo(X,z,mx,my,mz)
แบบนี้จะเห็นว่าการแบ่งถูกทำแค่พอประมาณ ไม่ละเอียดจนเกินไป
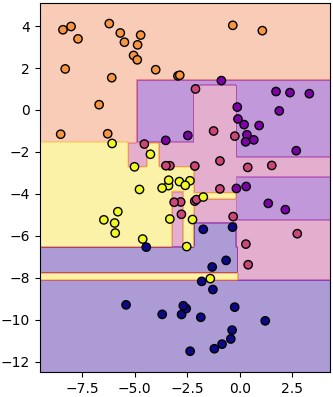
ในตัวอย่างที่ผ่านมาเราทำการแบ่งแค่ ๒ กลุ่ม แต่หากจะลองนำมาแบ่งเป็นหลายกลุ่มก็แน่นอนว่าทำได้เช่นกัน ลองดูได้เช่น
X,z = datasets.make_blobs(n_samples=100,n_features=2,centers=5,cluster_std=1.7,random_state=2)
tt = TonmaiTatsinchai(100)
tt.rianru(X,z)
mx,my = np.meshgrid(np.linspace(X[:,0].min()-1,X[:,0].max()+1,nmesh),np.linspace(X[:,1].min()-1,X[:,1].max()+1,nmesh))
mX = np.stack([mx,my],1)
mz = tt.thamnai(mX)
plottiamo(X,z,mx,my,mz)
สุดท้าย ขอลองสร้างเป็นภาพต้นไม้ขึ้นเพื่อเปรียบเทียบ ให้เห็นถึงภาพการแตกกิ่งของต้นไม้
สมมุติว่าต้นไม้แต่ละต้นคือข้อมูลชุดหนึ่งที่ต้องการแบ่งเป็น ๒ กลุ่ม เมื่อลองแตกกิ่งครั้งนึงเป็น ๒ ส่วนจะได้เป็นแบบนี้ พุ่มใบที่อยู่ตรงปลายยอดจะมีสีต่างกัน แสดงด้วยสีของกลุ่มที่มีจำนวนมากที่สุดในกิ่งนั้น ความกว้างของพุ่มใบแสดงถึงจำนวนข้อมูล

ถ้าแตกต่อเป็นรอบที่ ๒ แต่ละกิ่งก็จะย่อยลงไปอีก แต่จะเห็นได้ว่าบางกิ่งไม่ถูกแตกต่อแล้ว

แล้วก็แตกต่อไปอีกเป็นรอบที่ ๓, ๔ และ ๕ ก็จะเป็นแบบนี้



โดยสรุป ข้อดีและข้อเสียของวิธีการต้นไม้ตัดสินใจ
ข้อดี
- มองแล้วเข้าใจได้ง่าย ดูลำดับขั้นตอนการตัดสินใจแล้ววิเคราะห์ได้
- ไม่ขึ้นกับการกระจายตัวของข้อมูล ไม่จำเป็นต้องทำข้อมูลให้เป็นมาตรฐานก่อน
- จัดการแยกข้อมูลที่มีลักษณะเป็นเกาะลอยได้ดี
ข้อเสีย
- อาจแตกกิ่งมากไปทำให้เกิดการเรียนรู้เกินได้ง่าย
- หากข้อมูลเปลี่ยนแปลงแค่นิดเดียวผลการแตกกิ่งอาจเปลี่ยนไปคนละเรื่องเลยได้
- ไม่เหมาะกับข้อมูลที่มีลักษณะเป็นเชิงเส้น
- การแบ่งพิจารณาตัวแปรทีละตัวแยกกันตลอด ไม่สามารถใช้ตัวแปรสองชนิดขึ้นไปเป็นเกณฑ์ในการแบ่งพร้อมกันได้
วิธีการต้นไม้ตัดสินใจนั้นจริงๆแล้วมีรายละเอียดปลีกย่อยอะไรอีกมาก ซึ่งก็คงจะไม่ขอลงลึกแล้ว ในที่นี้แค่ต้องการเขียนแนวคิดคร่าวๆและพื้นฐานวิธีการสร้าง
หากต้องการใช้งานจริงๆอาจใช้ sklearn ซึ่งถูกเขียนมาอย่างดี สามารถปรับแต่งอะไรได้มากมาย เกี่ยวกับการใช้สามารถอ่านได้ใน https://phyblas.hinaboshi.com/20171108
อ้างอิง
-----------------------------------------
囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧囧
หมวดหมู่
-- คอมพิวเตอร์ >> ปัญญาประดิษฐ์-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> numpy
-- คอมพิวเตอร์ >> เขียนโปรแกรม >> python >> matplotlib